1.2.2 空间几何体的三视图
图片预览





文档简介
(共51张PPT)
1.2.2 空间几何体的三视图
鹿邑三高 史琳
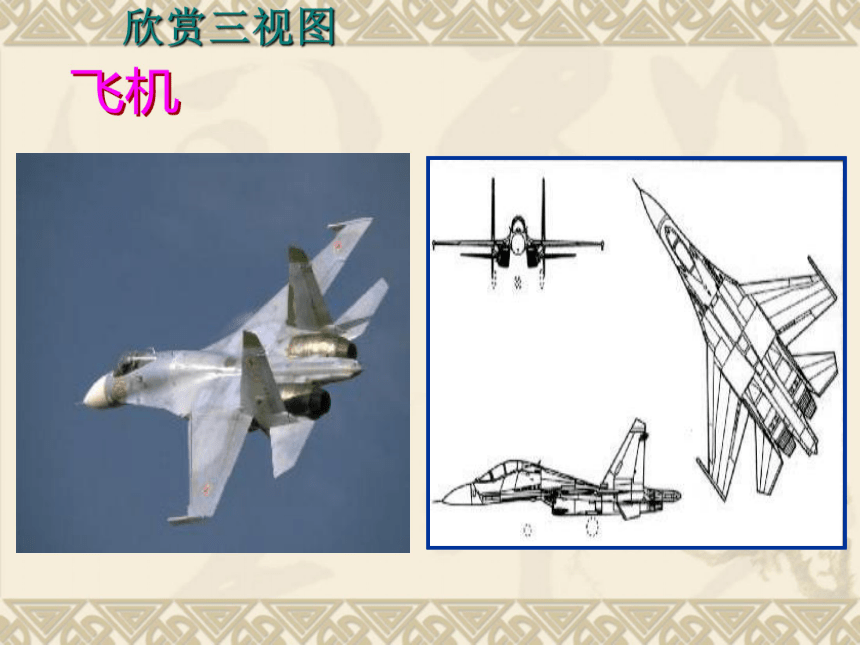
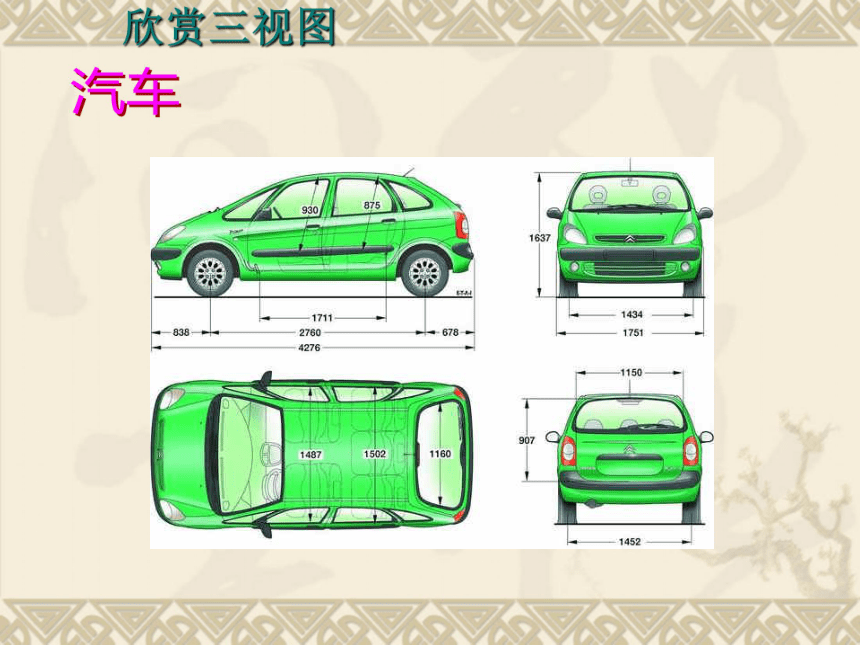
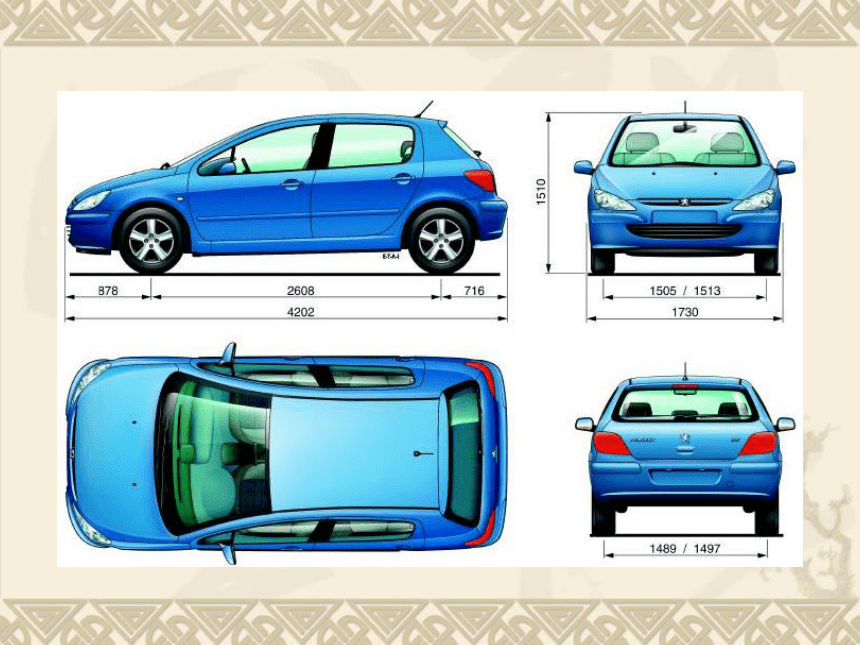
欣赏三视图
欣赏三视图
俯视图
正视图
俯视图
正视图
侧视图
侧视图
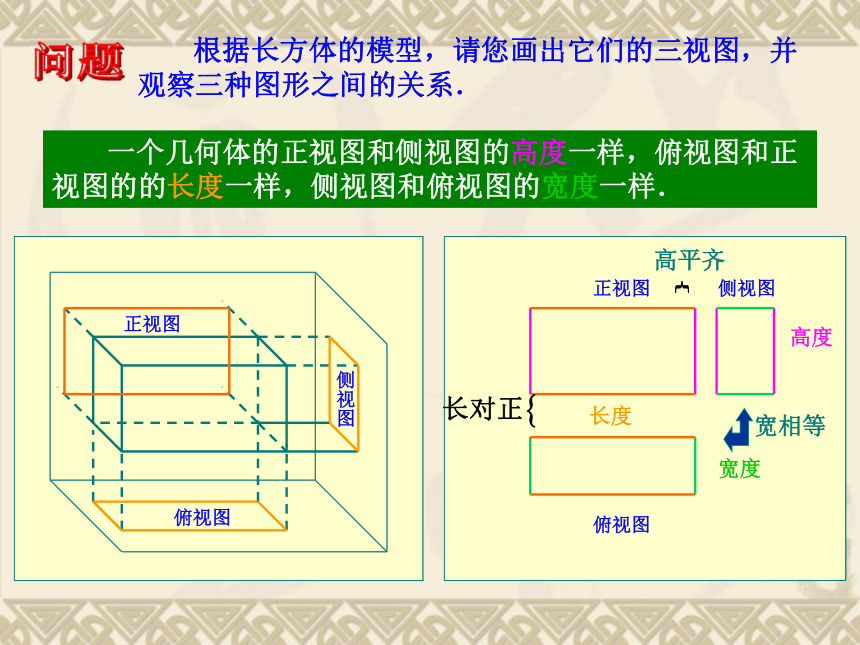
根据长方体的模型,请您画出它们的三视图,并观察三种图形之间的关系.
一个几何体的正视图和侧视图的高度一样,俯视图和正视图的的长度一样,侧视图和俯视图的宽度一样.
长度
高度
宽度
高平齐
宽相等
1.光线从几何体的前面向后面正投影所得到的投影图
叫做几何体的正视图.
2.光线从几何体的左面向右面正投影所得到的投影图
叫做几何体侧视图.
3.光线从几何体的上面向下面正投影所得到的投影图
叫做几何体的俯视图.
三视图
把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
结论:光线从几何体的前面向后面正投影,得到投影图,这种投影图叫做几何体的正视图(也叫主视图);光线从几何体的上面向下面正投影,得到投影图,这种投影图叫做几何体的俯视图;光线从几何体的左面向右面正投影,得到投影图,这种投影图叫做几何体的侧视图(也叫左视图);
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
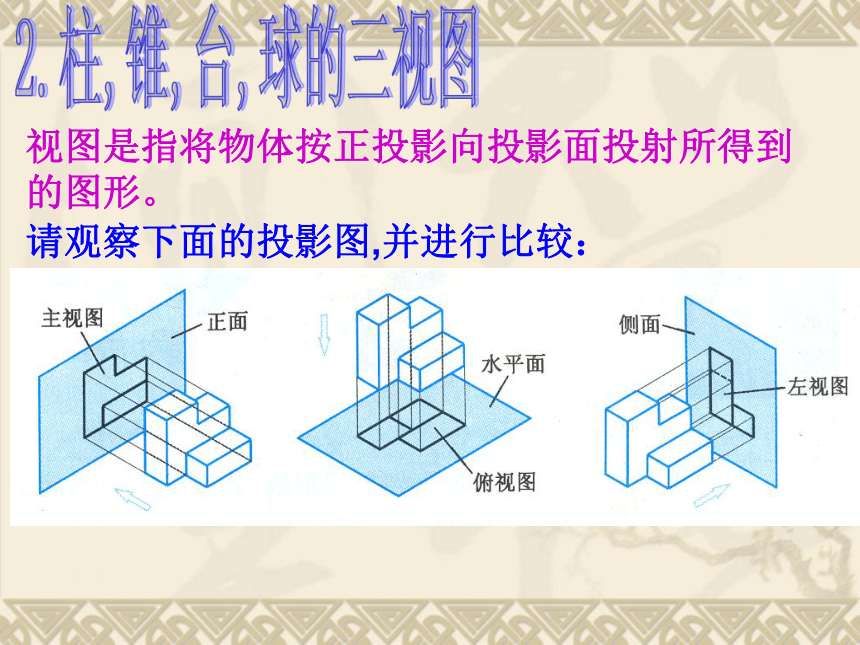
视图是指将物体按正投影向投影面投射所得到的图形。
请观察下面的投影图,并进行比较:
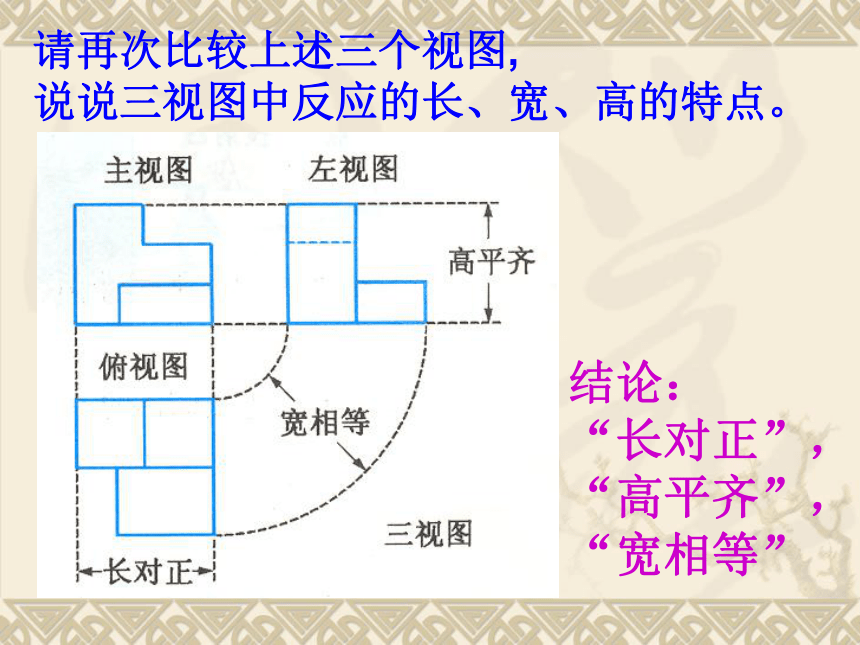
请再次比较上述三个视图,
说说三视图中反应的长、宽、高的特点。
结论:
“长对正”,
“高平齐”,
“宽相等”
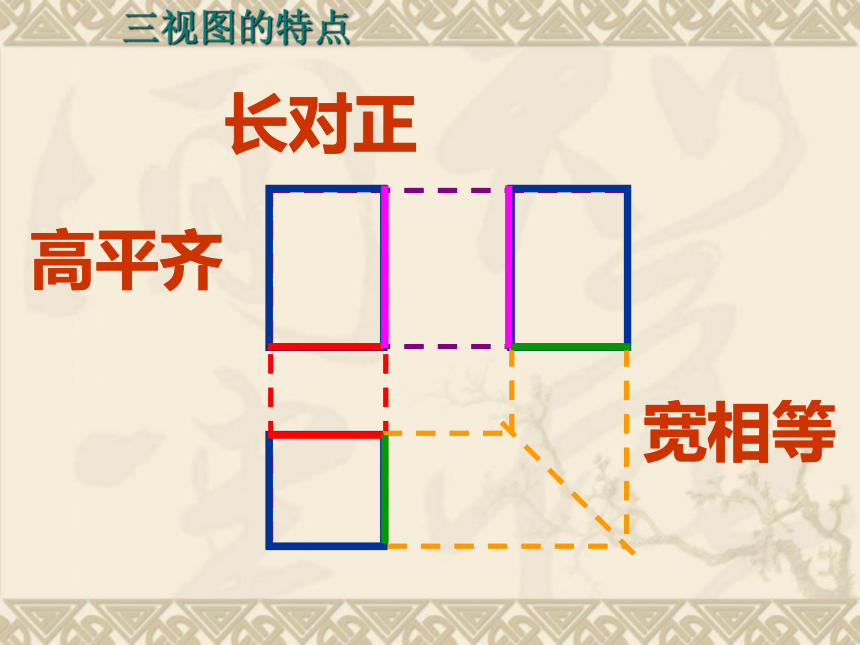
长对正
高平齐
宽相等
三视图的特点
正视图
侧视图
俯视图
正视图
侧视图
俯视图
·
圆柱 圆锥 球
请同学们画出下列几何图的三视图
正视图
侧视图
俯视图
三视图的作图步骤
正视图方向
侧视图方向
俯视图方向
2.运用长对正、高平齐、宽相等的原则画出其它视图
1 位置
正视图 侧视图 俯视图
从前面正对着物体观察,画出主视图,主视图反映了物体的长和高及前后两个面的实形.
从上向下正对着物体观察,画出俯视图,布置在主视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形.
三视图表达的意义
从左向右正对着物体观察,画出左视图,布置在主视图的正右方,左视图反映了物体的宽和高及左右两个面的实形.
三视图能反映物体真实的形状和长、宽、高.
侧视图
正视图
从正面看
从左面看
从上面看
俯视图
高
宽
宽
长
“正、俯视图长对正”
“正、侧视图高平齐”
“俯、侧视图宽相等’’
“长对正,高平齐,宽相等”是三视图之间的投影规律,是画图和读图的重要依据.
同学们能画出长方体的三视图吗
问题:
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆柱、圆锥、球的三视图.
正方体的三视图
主
左
俯
长方体
主
左
俯
长方体的三视图
六棱柱
主
左
俯
棱柱的三视图
棱锥的三视图
正四棱锥
主
左
俯
棱台的三视图
正四棱台
主
左
俯
圆柱
主
左
俯
圆柱的三视图
圆锥
主
左
俯
圆锥的三视图
圆台
主
左
俯
圆台的三视图
球体
主
左
俯
球的三视图
例1、画下例几何体的三视图
例2、画下例几何体的三视图
例3、画下例几何体的三视图
例四、画下例几何体的三视图
“视图”是将物体按正投影法向投影面投射时所得到的投影图.
光线自物体的前面向后投影所得的投影图称为“正视图” ,自左向右投影所得的投影图称为“侧视图”,自上向下投影所得的投影图称为“俯视图”.
用这三种视图即可刻划空间物体的几何结构,这种图称之为“三视图”.即向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图.
三视图有关概念
V正立投影面
H水平投影面
W侧立投影面
V
H
W
三视图的形成
W
V正视图
H
V
H俯视图
W侧视图
三视图的形成
俯视图
侧视图
正视图
三视图的形成
想一想:下列正三棱锥的三视图是怎样的
正三棱锥
主
左
俯
练一练:
试画出:四棱柱、四棱锥的三视图.
圆柱
正
侧
俯
请您画出圆柱的三视图
正
侧
俯
请您画出圆锥的三视图
正
侧
俯
请您画出圆台的三视图
正
侧
俯
请您画出六棱柱的三视图
请您画出六棱锥的三视图
正
侧
俯
正
侧
俯
请您画出四棱台的三视图
正
侧
俯
请您画出球的三视图
练习8、画下例几何体的三视图
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
侧视图
俯视图
四棱柱
由三视图想象几何体
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
侧视图
俯视图
圆锥
由三视图想象几何体
四棱锥
一个几何体的三视图如下,你能说出它是什么立体图形吗
由三视图想象几何体
如果要做一个水管的三叉接头,工人事先看到的不是图1,而是图2,然后根据这三个图形制造出水管接头.
图1
三通水管
图2
遮挡住看不见的线用虚线
画出下面这个组合图形的三视图.
圆锥
圆台
冰淇淋
请想象下面三视图所表示的几何图形的实物模型.
1.2.2 空间几何体的三视图
鹿邑三高 史琳
欣赏三视图
欣赏三视图
俯视图
正视图
俯视图
正视图
侧视图
侧视图
根据长方体的模型,请您画出它们的三视图,并观察三种图形之间的关系.
一个几何体的正视图和侧视图的高度一样,俯视图和正视图的的长度一样,侧视图和俯视图的宽度一样.
长度
高度
宽度
高平齐
宽相等
1.光线从几何体的前面向后面正投影所得到的投影图
叫做几何体的正视图.
2.光线从几何体的左面向右面正投影所得到的投影图
叫做几何体侧视图.
3.光线从几何体的上面向下面正投影所得到的投影图
叫做几何体的俯视图.
三视图
把一个空间几何体投影到一个平面上,可以获得一个平面图形.视图是指将物体按正投影向投影面投射所得到的图形.
但只有一个平面图形难以把握几何体的全貌,因此我们需要从多个角度进行投影.
结论:光线从几何体的前面向后面正投影,得到投影图,这种投影图叫做几何体的正视图(也叫主视图);光线从几何体的上面向下面正投影,得到投影图,这种投影图叫做几何体的俯视图;光线从几何体的左面向右面正投影,得到投影图,这种投影图叫做几何体的侧视图(也叫左视图);
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
视图是指将物体按正投影向投影面投射所得到的图形。
请观察下面的投影图,并进行比较:
请再次比较上述三个视图,
说说三视图中反应的长、宽、高的特点。
结论:
“长对正”,
“高平齐”,
“宽相等”
长对正
高平齐
宽相等
三视图的特点
正视图
侧视图
俯视图
正视图
侧视图
俯视图
·
圆柱 圆锥 球
请同学们画出下列几何图的三视图
正视图
侧视图
俯视图
三视图的作图步骤
正视图方向
侧视图方向
俯视图方向
2.运用长对正、高平齐、宽相等的原则画出其它视图
1 位置
正视图 侧视图 俯视图
从前面正对着物体观察,画出主视图,主视图反映了物体的长和高及前后两个面的实形.
从上向下正对着物体观察,画出俯视图,布置在主视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形.
三视图表达的意义
从左向右正对着物体观察,画出左视图,布置在主视图的正右方,左视图反映了物体的宽和高及左右两个面的实形.
三视图能反映物体真实的形状和长、宽、高.
侧视图
正视图
从正面看
从左面看
从上面看
俯视图
高
宽
宽
长
“正、俯视图长对正”
“正、侧视图高平齐”
“俯、侧视图宽相等’’
“长对正,高平齐,宽相等”是三视图之间的投影规律,是画图和读图的重要依据.
同学们能画出长方体的三视图吗
问题:
基本几何体的三视图
回忆初中已经学过的正方体、长方体、圆柱、圆锥、球的三视图.
正方体的三视图
主
左
俯
长方体
主
左
俯
长方体的三视图
六棱柱
主
左
俯
棱柱的三视图
棱锥的三视图
正四棱锥
主
左
俯
棱台的三视图
正四棱台
主
左
俯
圆柱
主
左
俯
圆柱的三视图
圆锥
主
左
俯
圆锥的三视图
圆台
主
左
俯
圆台的三视图
球体
主
左
俯
球的三视图
例1、画下例几何体的三视图
例2、画下例几何体的三视图
例3、画下例几何体的三视图
例四、画下例几何体的三视图
“视图”是将物体按正投影法向投影面投射时所得到的投影图.
光线自物体的前面向后投影所得的投影图称为“正视图” ,自左向右投影所得的投影图称为“侧视图”,自上向下投影所得的投影图称为“俯视图”.
用这三种视图即可刻划空间物体的几何结构,这种图称之为“三视图”.即向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图.
三视图有关概念
V正立投影面
H水平投影面
W侧立投影面
V
H
W
三视图的形成
W
V正视图
H
V
H俯视图
W侧视图
三视图的形成
俯视图
侧视图
正视图
三视图的形成
想一想:下列正三棱锥的三视图是怎样的
正三棱锥
主
左
俯
练一练:
试画出:四棱柱、四棱锥的三视图.
圆柱
正
侧
俯
请您画出圆柱的三视图
正
侧
俯
请您画出圆锥的三视图
正
侧
俯
请您画出圆台的三视图
正
侧
俯
请您画出六棱柱的三视图
请您画出六棱锥的三视图
正
侧
俯
正
侧
俯
请您画出四棱台的三视图
正
侧
俯
请您画出球的三视图
练习8、画下例几何体的三视图
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
侧视图
俯视图
四棱柱
由三视图想象几何体
下面是一些立体图形的三视图,请根据视图说出立体图形的名称:
正视图
侧视图
俯视图
圆锥
由三视图想象几何体
四棱锥
一个几何体的三视图如下,你能说出它是什么立体图形吗
由三视图想象几何体
如果要做一个水管的三叉接头,工人事先看到的不是图1,而是图2,然后根据这三个图形制造出水管接头.
图1
三通水管
图2
遮挡住看不见的线用虚线
画出下面这个组合图形的三视图.
圆锥
圆台
冰淇淋
请想象下面三视图所表示的几何图形的实物模型.
