2020-2021学年高二物理竞赛波的干涉课件(共34张PPT)
文档属性
| 名称 | 2020-2021学年高二物理竞赛波的干涉课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-21 20:26:02 | ||
图片预览









文档简介
(共34张PPT)
*
波的干涉
波频率相同,振动方向相同,位相差恒定
某些点振动始终加强,另一些点振动始终减弱或完全抵消.
(1)干涉现象
满足干涉条件的波称相干波.
(2)干涉条件
*
*
合振幅最大
当
合振幅最小
当
位相差 决定了合振幅的大小.
讨 论
干涉加强(相长)
干涉减弱(相消)
定值
*
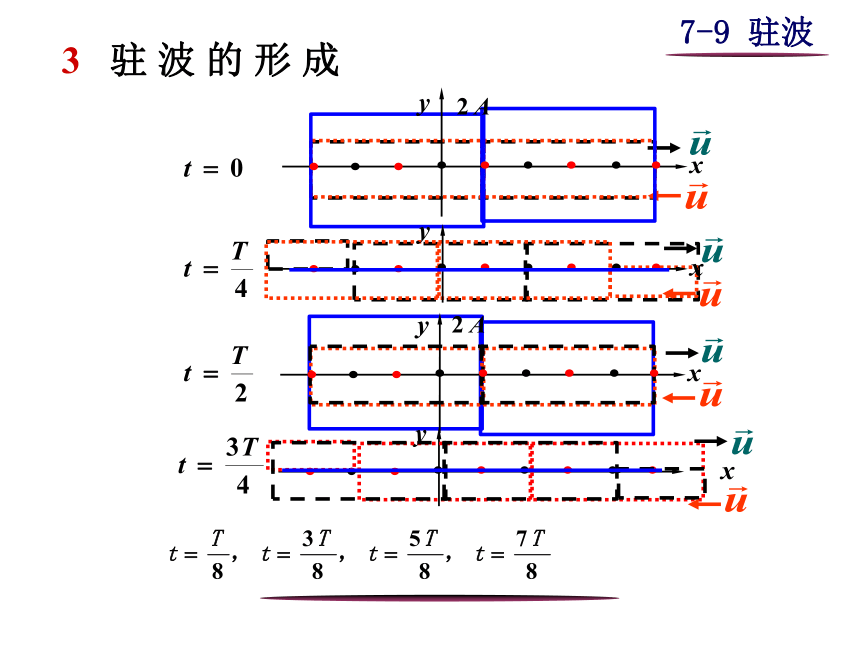
一 驻波的产生
2 现象
1 条件 两列振幅相同的相干波相向传播
3 驻 波 的 形 成
*
二 驻波方程
正向
负向
*
驻波方程
讨论
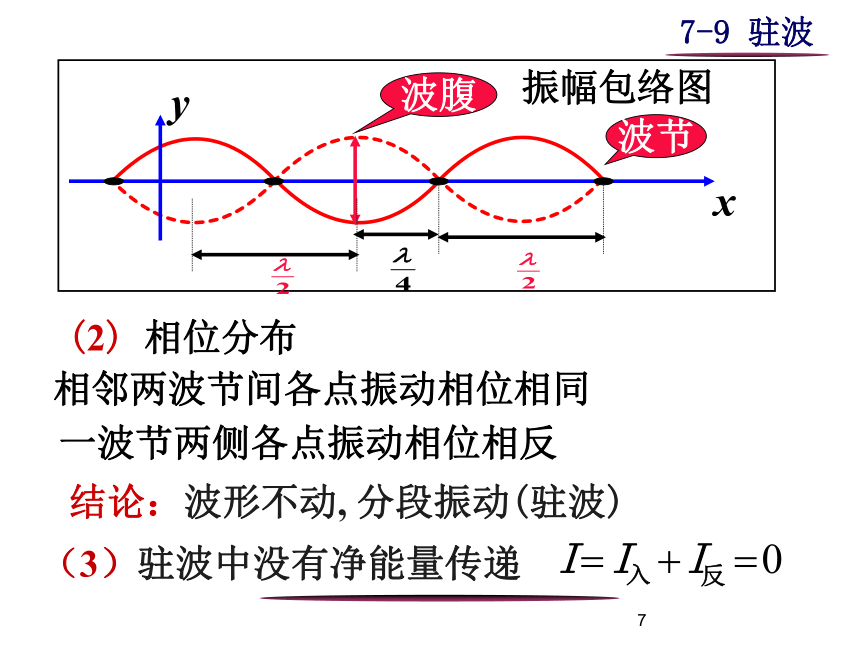
(1)振幅
当
处为波节
相邻波节间距:
每个点振幅恒定不变(与时间无关),不同质元的振幅不同。
处为波腹
当
相邻波腹间距:
*
x
y
波节
波腹
振幅包络图
(2) 相位分布
相邻两波节间各点振动相位相同
一波节两侧各点振动相位相反
(3)驻波中没有净能量传递
结论:波形不动, 分段振动(驻波)
*
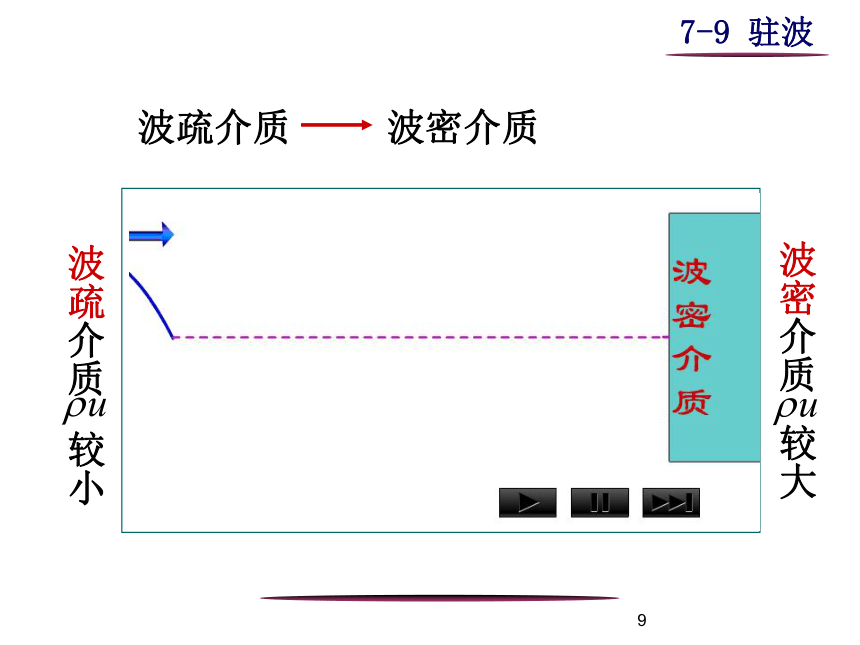
边界条件
驻波一般由入射、反射波叠加而成,反射发生在两介质交界面上,在交界面处出现波节还是波腹,取决于介质的性质.
波疏介质,波密介质
介质分类
*
波密介质
较大
波疏介质
较小
波疏介质 波密介质
*
当波从波疏介质垂直入射到波密介质,被反射到波疏介质时形成波节. 入射波与反射波在此处的相位时时相反, 即反射波在分界处产生 的相位跃变,相当于出现了半个波长的波程差,称半波损失.
三 相位跃变(半波损失)
*
*
当波从波密介质垂直入射到波疏介质, 被反射到波密介质时形成波腹. 入射波与反射波在此处的相位时时相同,即反射波在分界处不产生相位跃变.
波密介质 波疏介质
*
振动的简正模式
两端固定的弦线形成驻波时,波长 和弦线长 应满足
*
一端固定一端自由的弦振动的简正模式
*
例题 : 位于A、B两点的两个波源,振幅相等,频率都是100赫兹,相差为 ,其A、B 相距30米,波速为400米/秒,求: AB连线之间因相干涉而静止的各点的位置。
解:如图所示,取A点为坐标原点,A、B联线为X轴,取A点的振动方程 :
*
相干相消的点需满足:
可见在A、B两点是波腹处。
*
例 如图, 一列沿x轴正向传播的简谐波方程为 (m)
(1)
在1,2两种介质分界面上点A与坐标原点O相距L=2.25 m.已知介质2的波阻大于介质1的波阻, 反射波与入射波的振幅相等, 求:
(1)反射波方程;
(2)驻波方程;
(3)在OA之间波节和波腹的位置坐标.
y
L
O
A
x
1
2
*
解 (1)
由入射波方程得A点的入射振动方程
y
L
O
A
x
1
2
A点的反射振动
O点的反射振动
反射波方程为:
(m)
(2)
*
(2)
(3) 令
令
得波节坐标
≤
得波腹坐标
≤
练习波长为 的平面简谐波沿 x正向传播如图已知 Q 处振动方程为 , 波在M处遇一波密媒质反射面, 且假设反射波振幅仍为A。 求:
(1)该平面简谐波方程;
(2)反射波方程;
(3)驻波方程。
37
解:
(1)以Q 为参考点
37
(2)
以 P 为参考点,波由
所需时间
+
整理后得
反射波为
38
(3)
波腹
共10个波腹
入射波与反射波叠加成驻波,方程为
39
*
呜
人耳听到的声音的频率与声源的频率一定相同吗?
讨论
接收频率——单位时间内观测者接收到的振动次数或完整波数.
发射频率
接收频率
只有波源与观察者相对静止时才相等.
*
多普勒效应:当波源S和接收器R有相对运动时, 接收器所测得的频率不等于波源振动频率的现象
以介质为参考系,并设波源和观测者的运动都发生在它们之间的联线上.
vS—波源相对于介质的速度,趋近观察者为正;
v R —观察者相对介质的速度,趋近波源为正;
设波传播速度为u
*
观察者接收的频率
观察者向波源运动
观察者远离波源运动
一 波源不动,观察者相对介质以 运动
*
二 观察者不动,波源相对介质以 运动
*
A
*
波源向观察者运动
观察者接收的频率
波源远离观察者运动
A
*
三 波源与观察者同时相对介质运动
接近为+ ,远离为 -
*
若波源与观察者不沿二者连线运动
*
例1 利用多普勒效应监测车速,固定波源发出频率为 的超声波,当汽车向波源行驶时,与波源安装在一起的接收器接收到从汽车反射回来的波的频率为 .已知空气中的声速 , 求车速.
*
解 (1)车为接收器
车速
(2)车为波源
*
波的干涉
波频率相同,振动方向相同,位相差恒定
某些点振动始终加强,另一些点振动始终减弱或完全抵消.
(1)干涉现象
满足干涉条件的波称相干波.
(2)干涉条件
*
*
合振幅最大
当
合振幅最小
当
位相差 决定了合振幅的大小.
讨 论
干涉加强(相长)
干涉减弱(相消)
定值
*
一 驻波的产生
2 现象
1 条件 两列振幅相同的相干波相向传播
3 驻 波 的 形 成
*
二 驻波方程
正向
负向
*
驻波方程
讨论
(1)振幅
当
处为波节
相邻波节间距:
每个点振幅恒定不变(与时间无关),不同质元的振幅不同。
处为波腹
当
相邻波腹间距:
*
x
y
波节
波腹
振幅包络图
(2) 相位分布
相邻两波节间各点振动相位相同
一波节两侧各点振动相位相反
(3)驻波中没有净能量传递
结论:波形不动, 分段振动(驻波)
*
边界条件
驻波一般由入射、反射波叠加而成,反射发生在两介质交界面上,在交界面处出现波节还是波腹,取决于介质的性质.
波疏介质,波密介质
介质分类
*
波密介质
较大
波疏介质
较小
波疏介质 波密介质
*
当波从波疏介质垂直入射到波密介质,被反射到波疏介质时形成波节. 入射波与反射波在此处的相位时时相反, 即反射波在分界处产生 的相位跃变,相当于出现了半个波长的波程差,称半波损失.
三 相位跃变(半波损失)
*
*
当波从波密介质垂直入射到波疏介质, 被反射到波密介质时形成波腹. 入射波与反射波在此处的相位时时相同,即反射波在分界处不产生相位跃变.
波密介质 波疏介质
*
振动的简正模式
两端固定的弦线形成驻波时,波长 和弦线长 应满足
*
一端固定一端自由的弦振动的简正模式
*
例题 : 位于A、B两点的两个波源,振幅相等,频率都是100赫兹,相差为 ,其A、B 相距30米,波速为400米/秒,求: AB连线之间因相干涉而静止的各点的位置。
解:如图所示,取A点为坐标原点,A、B联线为X轴,取A点的振动方程 :
*
相干相消的点需满足:
可见在A、B两点是波腹处。
*
例 如图, 一列沿x轴正向传播的简谐波方程为 (m)
(1)
在1,2两种介质分界面上点A与坐标原点O相距L=2.25 m.已知介质2的波阻大于介质1的波阻, 反射波与入射波的振幅相等, 求:
(1)反射波方程;
(2)驻波方程;
(3)在OA之间波节和波腹的位置坐标.
y
L
O
A
x
1
2
*
解 (1)
由入射波方程得A点的入射振动方程
y
L
O
A
x
1
2
A点的反射振动
O点的反射振动
反射波方程为:
(m)
(2)
*
(2)
(3) 令
令
得波节坐标
≤
得波腹坐标
≤
练习波长为 的平面简谐波沿 x正向传播如图已知 Q 处振动方程为 , 波在M处遇一波密媒质反射面, 且假设反射波振幅仍为A。 求:
(1)该平面简谐波方程;
(2)反射波方程;
(3)驻波方程。
37
解:
(1)以Q 为参考点
37
(2)
以 P 为参考点,波由
所需时间
+
整理后得
反射波为
38
(3)
波腹
共10个波腹
入射波与反射波叠加成驻波,方程为
39
*
呜
人耳听到的声音的频率与声源的频率一定相同吗?
讨论
接收频率——单位时间内观测者接收到的振动次数或完整波数.
发射频率
接收频率
只有波源与观察者相对静止时才相等.
*
多普勒效应:当波源S和接收器R有相对运动时, 接收器所测得的频率不等于波源振动频率的现象
以介质为参考系,并设波源和观测者的运动都发生在它们之间的联线上.
vS—波源相对于介质的速度,趋近观察者为正;
v R —观察者相对介质的速度,趋近波源为正;
设波传播速度为u
*
观察者接收的频率
观察者向波源运动
观察者远离波源运动
一 波源不动,观察者相对介质以 运动
*
二 观察者不动,波源相对介质以 运动
*
A
*
波源向观察者运动
观察者接收的频率
波源远离观察者运动
A
*
三 波源与观察者同时相对介质运动
接近为+ ,远离为 -
*
若波源与观察者不沿二者连线运动
*
例1 利用多普勒效应监测车速,固定波源发出频率为 的超声波,当汽车向波源行驶时,与波源安装在一起的接收器接收到从汽车反射回来的波的频率为 .已知空气中的声速 , 求车速.
*
解 (1)车为接收器
车速
(2)车为波源
同课章节目录
