2021-2022学年鲁教版(五四制)九年级数学下册5.6直线与圆的位置关系 同步达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.6直线与圆的位置关系 同步达标测评(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 334.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学下册《5.6直线与圆的位置关系》同步达标测评(附答案)
一.选择题(共8小题,满分32分)
1.已知⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,那么直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
2.如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
A.①② B.①②③ C.①④ D.①②④
3.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
4.在平面直角坐标系中,⊙P的圆心坐标为(4,8),半径为5,那么x轴与⊙P的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
5.如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
A.15° B.20° C.25° D.30°
6.如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60° B.65° C.70° D.75°
7.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
8.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共6小题,满分30分)
9.如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是 .
10.如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为 .
11.如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是 .
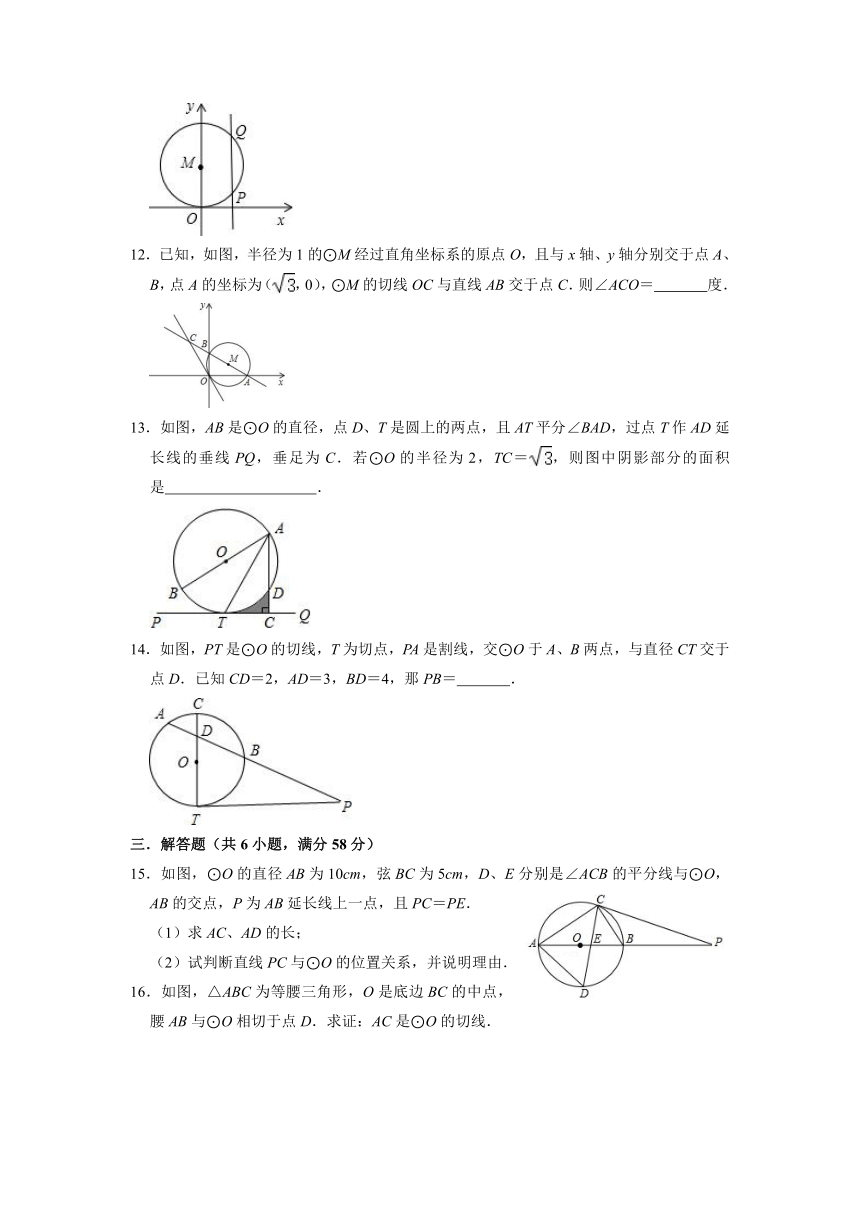
12.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO= 度.
13.如图,AB是⊙O的直径,点D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.若⊙O的半径为2,TC=,则图中阴影部分的面积是 .
14.如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB= .
三.解答题(共6小题,满分58分)
15.如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
16.如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
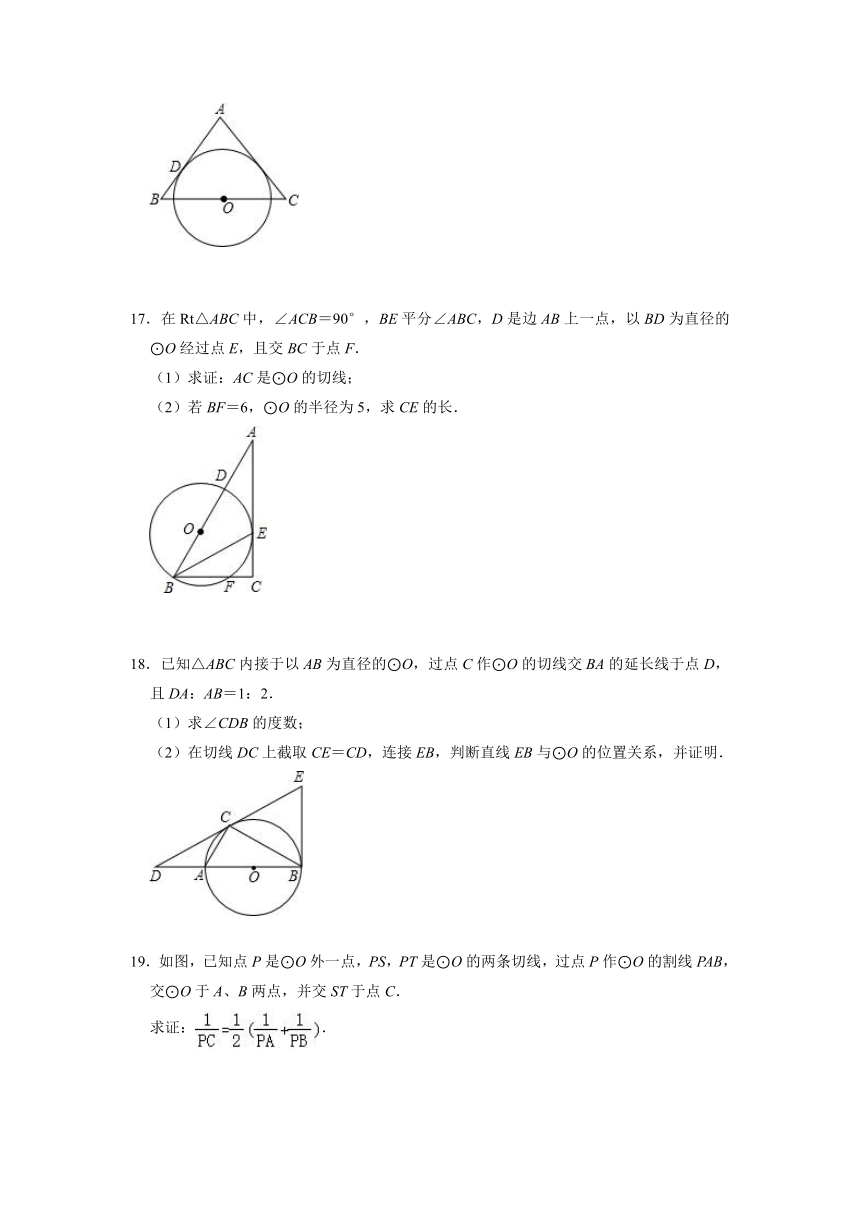
17.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
18.已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA:AB=1:2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
19.如图,已知点P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A、B两点,并交ST于点C.
求证:.
20.三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?
(3)探究:腰长为2的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?为什么?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
参考答案
一.选择题(共8小题,满分32分)
1.解:∴⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,
∴3.5<4,
∴直线l与⊙O的位置关系是相交,
故选:A.
2.解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC,
而AB=CB,
∴AD=DC,所以①正确;
∵AB=CB,
∴∠1=∠2,
而CD=ED,
∴∠3=∠4,
∵CF∥AB,
∴∠1=∠3,
∴∠1=∠2=∠3=∠4,
∴△CBA∽△CDE,所以②正确;
∵△ABC不能确定为直角三角形,
∴∠1不能确定等于45°,
∴与不能确定相等,所以③错误;
∵DA=DC=DE,
∴点E在以AC为直径的圆上,
∴∠AEC=90°,
∴CE⊥AE,
而CF∥AB,
∴AB⊥AE,
∴AE为⊙O的切线,所以④正确.
故选:D.
3.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
4.解:在直角坐标系内,以P(4,8)为圆心,5为半径画圆,则点P到x轴的距离为d=8,
∵r=5,
∴d>r,
∴⊙P与x轴的相离.
故选:B.
5.解:如图,连接OC.
∵OA=OC,
∴∠OAC=∠OCA=35°,
∴∠POC=∠OAC+∠OCA=70°,
∵PC是⊙O切线,
∴PC⊥OC,
∴∠PCO=90°,
∴∠P=90°﹣∠POC=20°,
故选:B.
6.解:连接OB,
∵PA、PB是⊙O的切线,A、B为切点,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°﹣∠P=140°,
由圆周角定理知,∠ACB=∠AOB=70°,
故选:C.
7.解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选:A.
8.解:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故(1)正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故(2)正确;
(3)连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
,
∴△PCO≌△BCA(ASA),
∴PO=AB,
故(3)正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,
∴∠PDB=120°,
故(4)正确;
正确个数有4个,
故选:A.
二.填空题(共6小题,满分30分)
9.解解:过点C作CD⊥AB于点D,
∵AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,
∴AB=5,
当直线与圆相切时,d=r,圆与斜边AB只有一个公共点,圆与斜边AB只有一个公共点,如图1,
∴CD×AB=AC×BC,
∴CD=r=,
当直线与圆如图所示也可以有一个交点,如图2,
∴3<r≤4,
故答案为:3<r≤4或r=.
10.解:∵OD∥BC,
∴∠AOD=∠B;
∵AD是⊙O的切线,
∴BA⊥AD,AB为圆O的直径,
∴∠OAD=∠ACB=90°,
∴Rt△AOD∽Rt△CBA,
∴,即,
故BC=.
11.解:连接MP,过P作PA⊥y轴于A,
设M点的坐标是(0,b),且b>0,
∵PA⊥y轴,
∴∠PAM=90°,
∴AP2+AM2=MP2,
∴22+(b﹣1)2=b2,
解得b=2.5, 故答案是(0,2.5).
12.解:∵AB=2,OA=,
∴cos∠BAO==,
∴∠OAB=30°,∠OBA=60°;
∵OC是⊙M的切线,
∴∠BOC=∠BAO=30°,
∴∠ACO=∠OBA﹣∠BOC=30°.
故答案为:30.
13.解:连接OT、OD、DT,过O作OM⊥AD于M,
∵OA=OT,AT平分∠BAC,
∴∠OTA=∠OAT,∠BAT=∠CAT,
∴∠OTA=∠CAT,
∴OT∥AC,
∵PC⊥AC,
∴OT⊥PC,
∵OT为半径,
∴PC是⊙O的切线,
∵OM⊥AC,AC⊥PC,OT⊥PC,
∴∠OMC=∠MCT=∠OTC=90°,
∴四边形OMCT是矩形,
∴OM=TC=,
∵OA=2,
∴sin∠OAM=,
∴∠OAM=60°,
∴∠AOM=30°
∵AC∥OT,
∴∠AOT=180°﹣∠OAM=120°,
∵∠OAM=60°,OA=OD,
∴△OAD是等边三角形,
∴∠AOD=60°,
∴∠TOD=120°﹣60°=60°,
∵PC切⊙O于T,
∴∠DTC=∠CAT=∠BAC=30°,
∴tan30°==,
∴DC=1,
∴阴影部分的面积是S梯形OTCD﹣S扇形OTD=×(2+1)×﹣=.
故答案为:.
14.解:∵AD BD=CD DT,
∴TD=,
∵CD=2,AD=3,BD=4,
∴TD=6,
∵PT是⊙O的切线,PA是割线,
∴PT2=PA PB,
∵CT为直径,
∴PT2=PD2﹣TD2,
∴PA PB=PD2﹣TD2,
即(PB+7)PB=(PB+4)2﹣62,
解得PB=20.
故答案为:20.
三.解答题(共6小题,满分58分)
15.解:(1)连接BD,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°',
∵CD平分∠ACB,
∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形,
∵AB=10,
∴AD=BD==5,
在Rt△ACB中,AB=10,BC=5,
∴AC==5,
答:AC=5,AD=5;
(2)直线PC与⊙O相切,理由是:
连接OC,
在Rt△ACB中,AB=10,BC=5,
∴∠BAC=30°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠COB=60°,
∵∠ACD=45°,
∴∠OCD=45°﹣30°=15°,
∴∠CEP=∠COB+∠OCD=15°+60°=75°,
∵PC=PE,
∴∠PCE=∠CEP=75°,
∴∠OCP=∠OCD+∠ECP=15°+75°=90°,
∴直线PC与⊙O相切.
16.证明:过点O作OE⊥AC于点E,连接OD,OA,
∵AB与⊙O相切于点D,
∴AB⊥OD,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径,
∵AC经过⊙O的半径OE的外端点且垂直于OE,
∴AC是⊙O的切线.
17.(1)证明:连接OE.
∵OE=OB,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠C,
∵∠ACB=90°,
∴∠OEA=90°
∴AC是⊙O的切线;
(2)解:连接OE、OF,过点O作OH⊥BF交BF于H,
由题意可知四边形OECH为矩形,
∴OH=CE,
∵BF=6,
∴BH=3,
在Rt△BHO中,OB=5,
∴OH==4,
∴CE=4.
18.解:(1)连接OC,∵CD是⊙O的切线,
∴∠OCD=90°.
设⊙O的半径为R,则AB=2R,
∵DA:AB=1:2,
∴DA=R,DO=2R.
∴A为DO的中点,
∴AC=DO=R,
∴AC=CO=AO,
∴三角形ACO为等边三角形
∴∠COD=60°,即∠CDB=30°.
(2)直线EB与⊙O相切.
证明:连接OC,
由(1)可知∠CDO=30°,
∴∠COD=60°.
∵OC=OB,
∴∠OBC=∠OCB=30°
.∴∠CBD=∠CDB.
∴CD=CB.
∵CD是⊙O的切线,
∴∠OCE=90°.
∴∠ECB=60°.
又∵CD=CE,
∴CB=CE.
∴△CBE为等边三角形.
∴∠EBA=∠EBC+∠CBD=90°.
∴EB是⊙O的切线.
19.证明:连PO交ST于点D,则PO⊥ST;
连SO,作OE⊥PB于E,则E为AB中点,
于是
因为C、E、O、D四点共圆,
所以PC PE=PD PO
又因为Rt△SPD∽Rt△OPS
所以
即PS2=PD PO
而由切割线定理知PS2=PA PB
所以
即
20.(1)答:一个有内心的四边形是菱形.
(2)答:对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等.
(3)解:有无数条,
作△ABC的内切圆,切AC、BC于M、N,在弧MN 上任取一点作内切圆圆的切线,即为裁剪线.
(4)
解:等腰直角△ACB,AC=BC=2,由勾股定理得:AB=2,
过D作DF⊥AB于F,过E作EQ⊥AB于Q,
∴DF∥EQ,
∵DE∥AB,
∴四边形DEQF是平行四边形,
∴DE=FQ,DF=EQ,
∵∠A=∠B=45°,
∴AF=DF,
同理BQ=QE,
设DE=x,AB=2,过C作CM⊥BC,交DE与N点,
由BC=AC,根据三线合一可得CM=,
由三角形的面积有两种求法,S=AC BC=(AC+BC+AB) OM,
即4=(2+2+2)×OM,解得:OM=2﹣,
∴NM=2OM=4﹣2,CN=﹣(4﹣2)=3﹣4,
又△CDE∽△CAB,
∴=,即=,
解得:x=6﹣8,
则DE=6﹣8.
一.选择题(共8小题,满分32分)
1.已知⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,那么直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不确定
2.如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
A.①② B.①②③ C.①④ D.①②④
3.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
4.在平面直角坐标系中,⊙P的圆心坐标为(4,8),半径为5,那么x轴与⊙P的位置关系是( )
A.相交 B.相离 C.相切 D.以上都不是
5.如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线PC与AB的延长线交于点P,则∠P等于( )
A.15° B.20° C.25° D.30°
6.如图,PA和PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
A.60° B.65° C.70° D.75°
7.有下列结论:(1)平分弦的直径垂直于弦;(2)圆周角的度数等于圆心角的一半;(3)等弧所对的圆周角相等;(4)经过三点一定可以作一个圆;(5)三角形的外心到三边的距离相等;(6)垂直于半径的直线是圆的切线.
其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
8.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共6小题,满分30分)
9.如图,在△ABC中,∠C=90°,AC=3,BC=4,若以C为圆心,R为半径的圆与斜边AB只有一个公共点,则R的值是 .
10.如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为 .
11.如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是 .
12.已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为(,0),⊙M的切线OC与直线AB交于点C.则∠ACO= 度.
13.如图,AB是⊙O的直径,点D、T是圆上的两点,且AT平分∠BAD,过点T作AD延长线的垂线PQ,垂足为C.若⊙O的半径为2,TC=,则图中阴影部分的面积是 .
14.如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB= .
三.解答题(共6小题,满分58分)
15.如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
16.如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.
17.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
18.已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA:AB=1:2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
19.如图,已知点P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A、B两点,并交ST于点C.
求证:.
20.三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?
(3)探究:腰长为2的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?为什么?
(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
参考答案
一.选择题(共8小题,满分32分)
1.解:∴⊙O的半径为4cm,如果圆心O到直线l的距离为3.5cm,
∴3.5<4,
∴直线l与⊙O的位置关系是相交,
故选:A.
2.解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC,
而AB=CB,
∴AD=DC,所以①正确;
∵AB=CB,
∴∠1=∠2,
而CD=ED,
∴∠3=∠4,
∵CF∥AB,
∴∠1=∠3,
∴∠1=∠2=∠3=∠4,
∴△CBA∽△CDE,所以②正确;
∵△ABC不能确定为直角三角形,
∴∠1不能确定等于45°,
∴与不能确定相等,所以③错误;
∵DA=DC=DE,
∴点E在以AC为直径的圆上,
∴∠AEC=90°,
∴CE⊥AE,
而CF∥AB,
∴AB⊥AE,
∴AE为⊙O的切线,所以④正确.
故选:D.
3.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
4.解:在直角坐标系内,以P(4,8)为圆心,5为半径画圆,则点P到x轴的距离为d=8,
∵r=5,
∴d>r,
∴⊙P与x轴的相离.
故选:B.
5.解:如图,连接OC.
∵OA=OC,
∴∠OAC=∠OCA=35°,
∴∠POC=∠OAC+∠OCA=70°,
∵PC是⊙O切线,
∴PC⊥OC,
∴∠PCO=90°,
∴∠P=90°﹣∠POC=20°,
故选:B.
6.解:连接OB,
∵PA、PB是⊙O的切线,A、B为切点,
∴∠OAP=∠OBP=90°,
∴∠AOB=180°﹣∠P=140°,
由圆周角定理知,∠ACB=∠AOB=70°,
故选:C.
7.解:(1)应强调这条弦不是直径;故本选项错误;
(2)应强调在同圆或等圆中,同弧所对的圆周角的度数等于圆心角的一半;故本选项错误;
(3)等弧弧所对的圆周角的度数等于圆心角的一半;故本选项正确;
(4)必须不在同一条直线上的三个点才能确定一个圆,故本选项错误;
(5)三角形的外心是三角形三条边的垂直平分线的交点,所以三角形的外心到三角形三个顶点的距离相等,故本选项错误;
(6)应该是过圆上一点且垂直圆的半径的直线是圆的切线;故本选项错误;
综上所述,正确的个数是1个;
故选:A.
8.解:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故(1)正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故(2)正确;
(3)连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
,
∴△PCO≌△BCA(ASA),
∴PO=AB,
故(3)正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,
∴∠PDB=120°,
故(4)正确;
正确个数有4个,
故选:A.
二.填空题(共6小题,满分30分)
9.解解:过点C作CD⊥AB于点D,
∵AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,
∴AB=5,
当直线与圆相切时,d=r,圆与斜边AB只有一个公共点,圆与斜边AB只有一个公共点,如图1,
∴CD×AB=AC×BC,
∴CD=r=,
当直线与圆如图所示也可以有一个交点,如图2,
∴3<r≤4,
故答案为:3<r≤4或r=.
10.解:∵OD∥BC,
∴∠AOD=∠B;
∵AD是⊙O的切线,
∴BA⊥AD,AB为圆O的直径,
∴∠OAD=∠ACB=90°,
∴Rt△AOD∽Rt△CBA,
∴,即,
故BC=.
11.解:连接MP,过P作PA⊥y轴于A,
设M点的坐标是(0,b),且b>0,
∵PA⊥y轴,
∴∠PAM=90°,
∴AP2+AM2=MP2,
∴22+(b﹣1)2=b2,
解得b=2.5, 故答案是(0,2.5).
12.解:∵AB=2,OA=,
∴cos∠BAO==,
∴∠OAB=30°,∠OBA=60°;
∵OC是⊙M的切线,
∴∠BOC=∠BAO=30°,
∴∠ACO=∠OBA﹣∠BOC=30°.
故答案为:30.
13.解:连接OT、OD、DT,过O作OM⊥AD于M,
∵OA=OT,AT平分∠BAC,
∴∠OTA=∠OAT,∠BAT=∠CAT,
∴∠OTA=∠CAT,
∴OT∥AC,
∵PC⊥AC,
∴OT⊥PC,
∵OT为半径,
∴PC是⊙O的切线,
∵OM⊥AC,AC⊥PC,OT⊥PC,
∴∠OMC=∠MCT=∠OTC=90°,
∴四边形OMCT是矩形,
∴OM=TC=,
∵OA=2,
∴sin∠OAM=,
∴∠OAM=60°,
∴∠AOM=30°
∵AC∥OT,
∴∠AOT=180°﹣∠OAM=120°,
∵∠OAM=60°,OA=OD,
∴△OAD是等边三角形,
∴∠AOD=60°,
∴∠TOD=120°﹣60°=60°,
∵PC切⊙O于T,
∴∠DTC=∠CAT=∠BAC=30°,
∴tan30°==,
∴DC=1,
∴阴影部分的面积是S梯形OTCD﹣S扇形OTD=×(2+1)×﹣=.
故答案为:.
14.解:∵AD BD=CD DT,
∴TD=,
∵CD=2,AD=3,BD=4,
∴TD=6,
∵PT是⊙O的切线,PA是割线,
∴PT2=PA PB,
∵CT为直径,
∴PT2=PD2﹣TD2,
∴PA PB=PD2﹣TD2,
即(PB+7)PB=(PB+4)2﹣62,
解得PB=20.
故答案为:20.
三.解答题(共6小题,满分58分)
15.解:(1)连接BD,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°',
∵CD平分∠ACB,
∴∠ACD=∠DCB=45°,
∴∠ABD=∠ACD=45°,∠DAB=∠DCB=45°,
∴△ADB是等腰直角三角形,
∵AB=10,
∴AD=BD==5,
在Rt△ACB中,AB=10,BC=5,
∴AC==5,
答:AC=5,AD=5;
(2)直线PC与⊙O相切,理由是:
连接OC,
在Rt△ACB中,AB=10,BC=5,
∴∠BAC=30°,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∴∠COB=60°,
∵∠ACD=45°,
∴∠OCD=45°﹣30°=15°,
∴∠CEP=∠COB+∠OCD=15°+60°=75°,
∵PC=PE,
∴∠PCE=∠CEP=75°,
∴∠OCP=∠OCD+∠ECP=15°+75°=90°,
∴直线PC与⊙O相切.
16.证明:过点O作OE⊥AC于点E,连接OD,OA,
∵AB与⊙O相切于点D,
∴AB⊥OD,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径,
∵AC经过⊙O的半径OE的外端点且垂直于OE,
∴AC是⊙O的切线.
17.(1)证明:连接OE.
∵OE=OB,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠C,
∵∠ACB=90°,
∴∠OEA=90°
∴AC是⊙O的切线;
(2)解:连接OE、OF,过点O作OH⊥BF交BF于H,
由题意可知四边形OECH为矩形,
∴OH=CE,
∵BF=6,
∴BH=3,
在Rt△BHO中,OB=5,
∴OH==4,
∴CE=4.
18.解:(1)连接OC,∵CD是⊙O的切线,
∴∠OCD=90°.
设⊙O的半径为R,则AB=2R,
∵DA:AB=1:2,
∴DA=R,DO=2R.
∴A为DO的中点,
∴AC=DO=R,
∴AC=CO=AO,
∴三角形ACO为等边三角形
∴∠COD=60°,即∠CDB=30°.
(2)直线EB与⊙O相切.
证明:连接OC,
由(1)可知∠CDO=30°,
∴∠COD=60°.
∵OC=OB,
∴∠OBC=∠OCB=30°
.∴∠CBD=∠CDB.
∴CD=CB.
∵CD是⊙O的切线,
∴∠OCE=90°.
∴∠ECB=60°.
又∵CD=CE,
∴CB=CE.
∴△CBE为等边三角形.
∴∠EBA=∠EBC+∠CBD=90°.
∴EB是⊙O的切线.
19.证明:连PO交ST于点D,则PO⊥ST;
连SO,作OE⊥PB于E,则E为AB中点,
于是
因为C、E、O、D四点共圆,
所以PC PE=PD PO
又因为Rt△SPD∽Rt△OPS
所以
即PS2=PD PO
而由切割线定理知PS2=PA PB
所以
即
20.(1)答:一个有内心的四边形是菱形.
(2)答:对于任意四边形ABCD,如果有内心,则四边形的边长具备条件是对边和相等.
(3)解:有无数条,
作△ABC的内切圆,切AC、BC于M、N,在弧MN 上任取一点作内切圆圆的切线,即为裁剪线.
(4)
解:等腰直角△ACB,AC=BC=2,由勾股定理得:AB=2,
过D作DF⊥AB于F,过E作EQ⊥AB于Q,
∴DF∥EQ,
∵DE∥AB,
∴四边形DEQF是平行四边形,
∴DE=FQ,DF=EQ,
∵∠A=∠B=45°,
∴AF=DF,
同理BQ=QE,
设DE=x,AB=2,过C作CM⊥BC,交DE与N点,
由BC=AC,根据三线合一可得CM=,
由三角形的面积有两种求法,S=AC BC=(AC+BC+AB) OM,
即4=(2+2+2)×OM,解得:OM=2﹣,
∴NM=2OM=4﹣2,CN=﹣(4﹣2)=3﹣4,
又△CDE∽△CAB,
∴=,即=,
解得:x=6﹣8,
则DE=6﹣8.
