2021-2022学年鲁教版(五四制)九年级数学下册5.8正多边形和圆 同步达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.8正多边形和圆 同步达标测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 432.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 07:18:22 | ||
图片预览

文档简介
2021-2022学年鲁教版九年级数学下册《5.8正多边形和圆》同步达标测评(附答案)
一.选择题(共9小题,满分36分)
1.如图,点A,B,C,D,E,F,G,H为⊙O的八等分点,AD与BH的交点为I,若⊙O的半径为1,则HI的长等于( )
A.2﹣ B.2+ C.2 D.
2.把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )
A.1 B.2 C. D.2
3.如图,在正五边形ABCDE中,连接AC,BE,BD,AC与BE,BD分别交于点F,G,若AB=2,则FG的长为( )
A.3﹣ B.﹣1 C. D.2﹣3
4.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3 B.:1 C.: D.1:
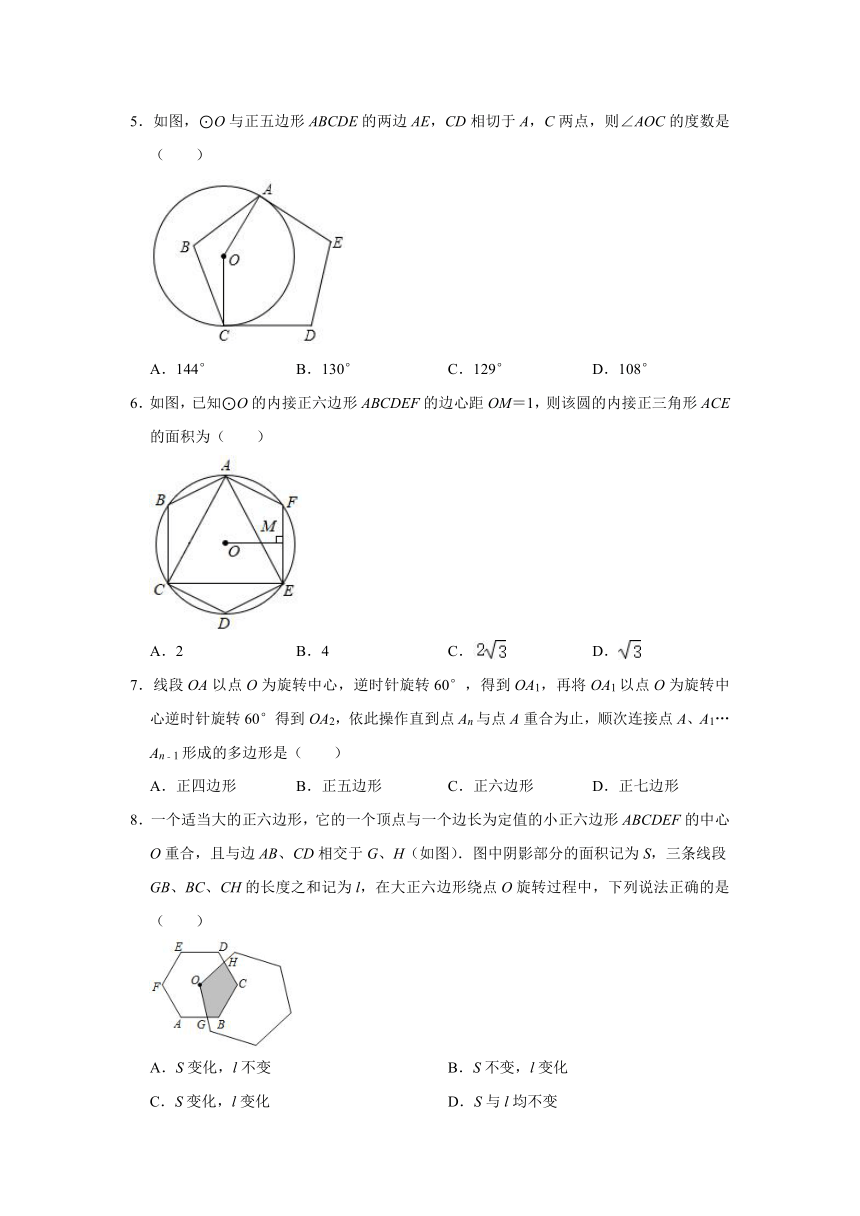
5.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
6.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=1,则该圆的内接正三角形ACE的面积为( )
A.2 B.4 C. D.
7.线段OA以点O为旋转中心,逆时针旋转60°,得到OA1,再将OA1以点O为旋转中心逆时针旋转60°得到OA2,依此操作直到点An与点A重合为止,顺次连接点A、A1…An﹣1形成的多边形是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
8.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
9.如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是( )
A.(20+10)cm B.(30+10)cm C.(20+20)cm D.40cm
二.填空题(共5小题,满分20分)
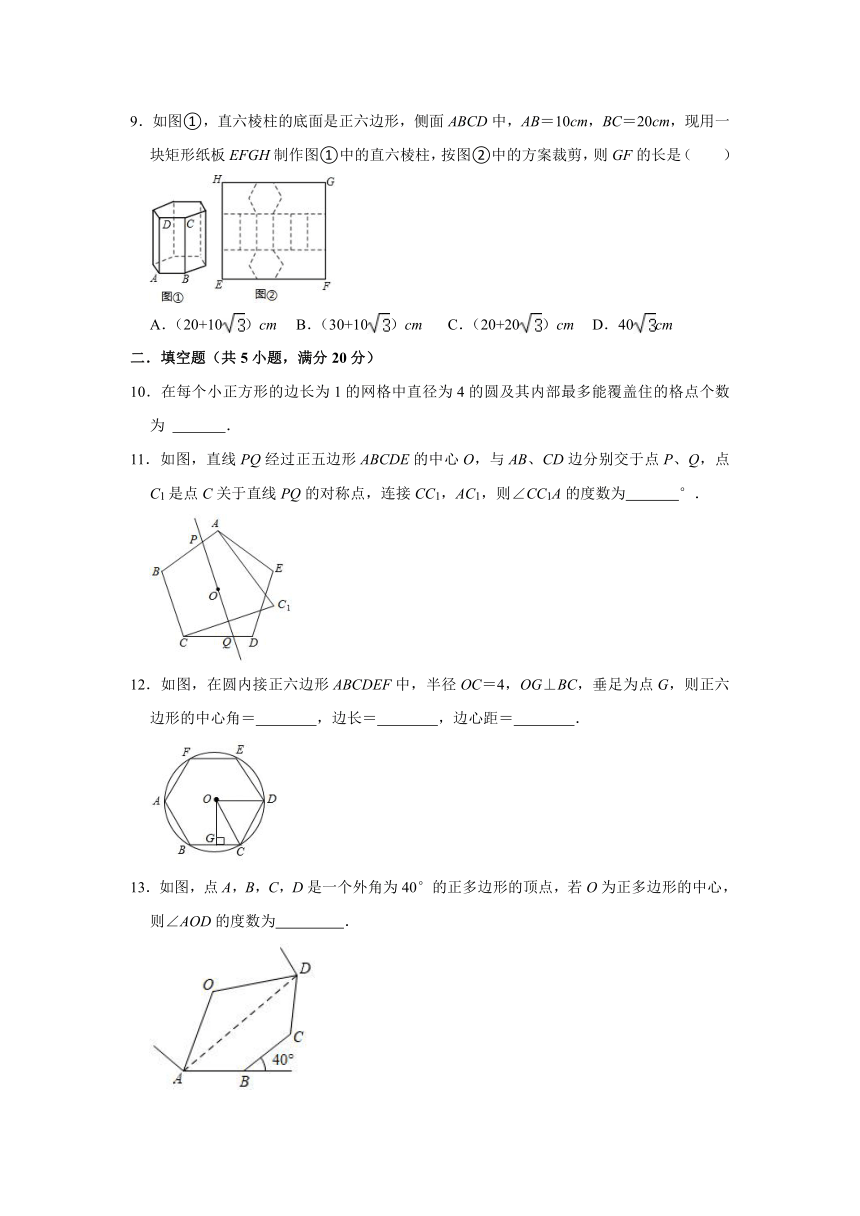
10.在每个小正方形的边长为1的网格中直径为4的圆及其内部最多能覆盖住的格点个数为 .
11.如图,直线PQ经过正五边形ABCDE的中心O,与AB、CD边分别交于点P、Q,点C1是点C关于直线PQ的对称点,连接CC1,AC1,则∠CC1A的度数为 °.
12.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= ,边长= ,边心距= .
13.如图,点A,B,C,D是一个外角为40°的正多边形的顶点,若O为正多边形的中心,则∠AOD的度数为 .
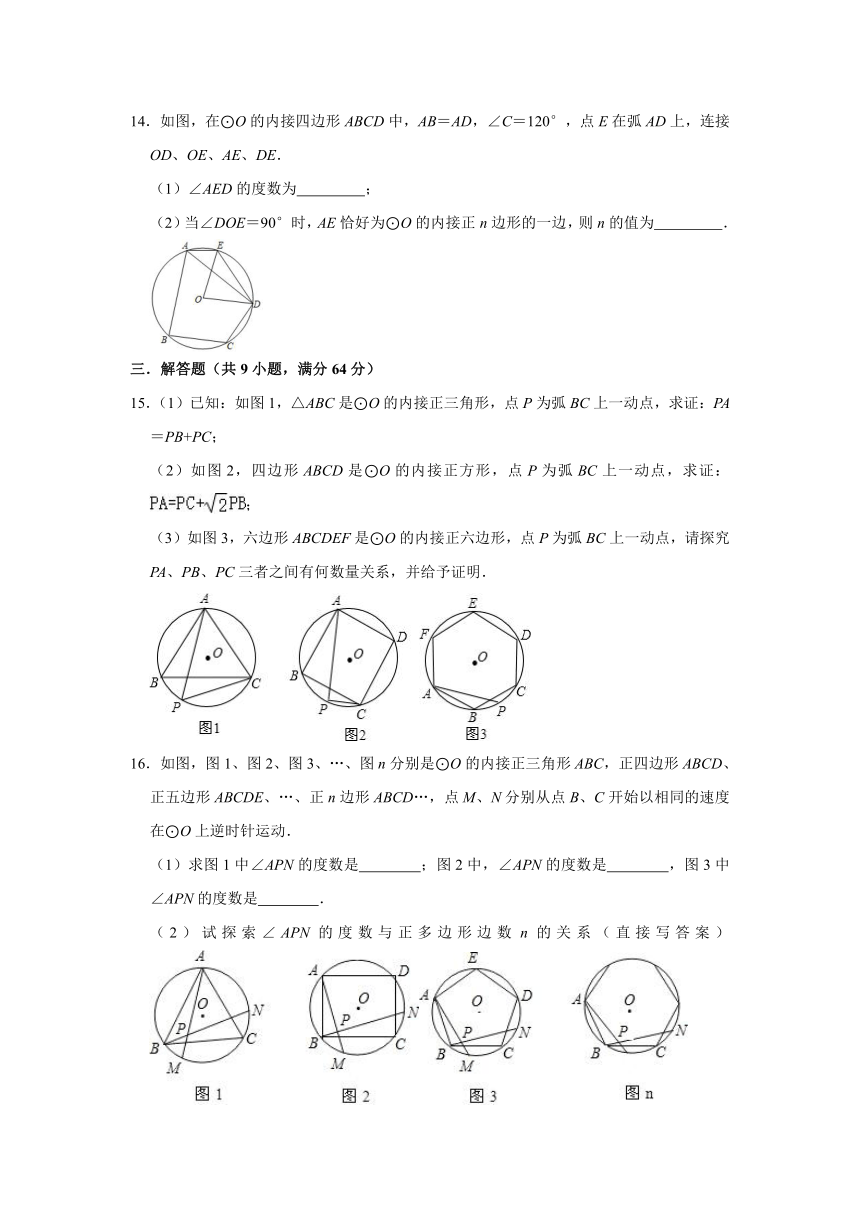
14.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上,连接OD、OE、AE、DE.
(1)∠AED的度数为 ;
(2)当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,则n的值为 .
三.解答题(共9小题,满分64分)
15.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:;
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,并给予证明.
16.如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数是 ;图2中,∠APN的度数是 ,图3中∠APN的度数是 .
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
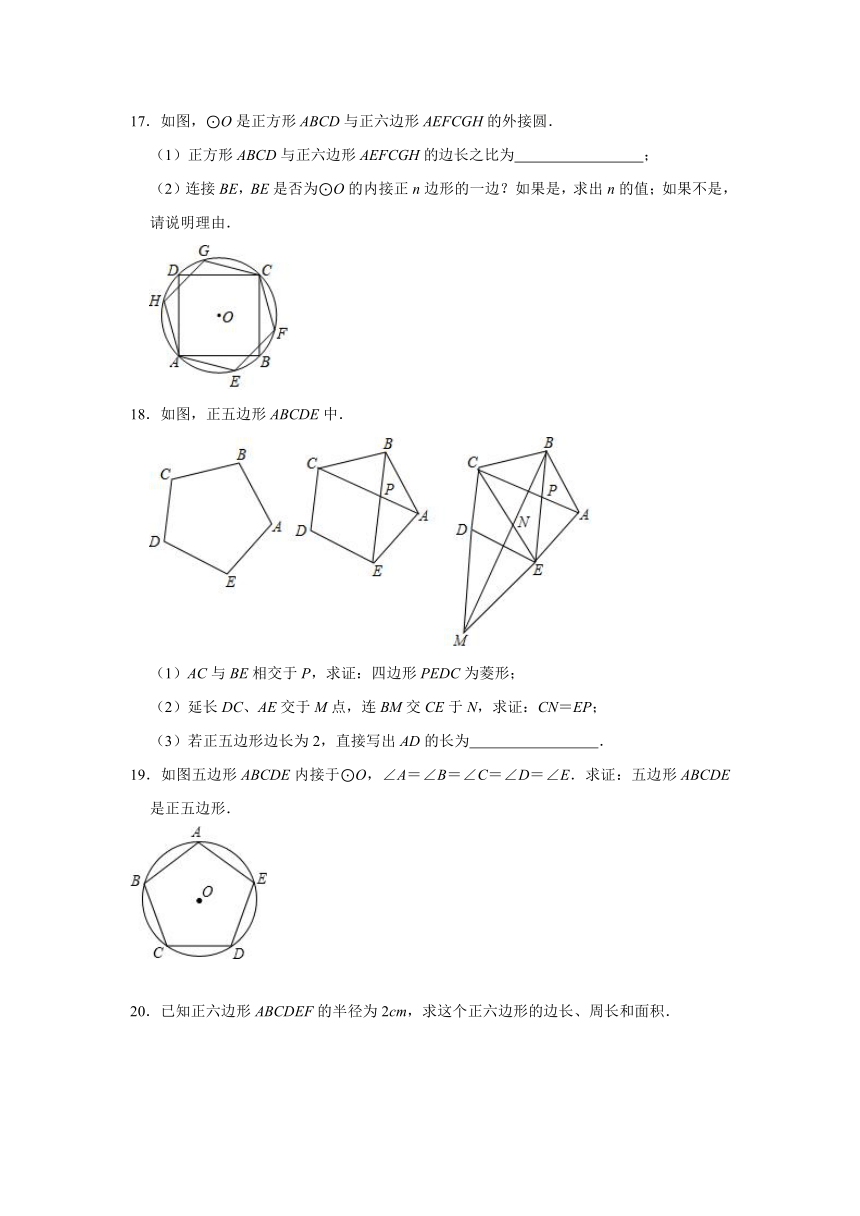
17.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1)正方形ABCD与正六边形AEFCGH的边长之比为 ;
(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
18.如图,正五边形ABCDE中.
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
19.如图五边形ABCDE内接于⊙O,∠A=∠B=∠C=∠D=∠E.求证:五边形ABCDE是正五边形.
20.已知正六边形ABCDEF的半径为2cm,求这个正六边形的边长、周长和面积.
21.如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.
22.如图,在正六边形ABCDEF中,以AD为对角线作正方形APDQ,AP、DP与BC分别交于M、N.
(1)∠BAM= °;
(2)若AB=4,求MN的长.(参考数据:≈1.73,结果精确到0.1,可以直接利用(1)的结论)
23.如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
参考答案
一.选择题(共9小题,满分36分)
1.解:如图,连接AB、OH,作OM⊥AD于M,ON⊥BH于N,在IH上截取一点K,使得ON=NK,连接OK.
∵点A,B,C,D,E,F,G,H为⊙O的八等分点,
∴∠A=∠B=45°,∠H=22.5°,
∴∠AIB=90°,
∴∠MIN=∠OMI=∠ONI=90°,
∴四边形OMIN是矩形,
∵=,
∴AD=BH,
∴OM=ON,
∴四边形OMIN是正方形,设OM=a,
∵ON=NK,
∴∠OKN=45°,
∵∠OKN=∠H+∠KOH,
∴∠H=∠KOH=22.5°,
∴OK=KN=a,
在Rt△ONH中,a2+(a+a)2=1,
∴a=,
∴IH=(2+)a=.
故选:D.
2.解:如图,
∵重叠部分为正八边形的一半,
∴GF=EF=PE=HP,∠GFE=∠FEP=∠HPE=135°,
∴∠GFC=∠B'FE=∠DEP=∠A'PH=45°,
∴△CGF、△B'EF是全等的等腰直角三角形,
设CG=x,则GF=x,B'F=x,
∴BG=B'G=x+x,
∴BC=x+x+x=2+,
∴x=1,
∴GF=,
故选:C.
3.解:∵五边形ABCDE是正五边形,
∴∠BAF=∠ABF=∠DBE=36°,
∴FA=FB,
∴∠ABG=∠AGB=∠BFG=72°,
∴AB=AG=2,BG=BF,
设AF=BF=BG=x,
∵∠BGF=∠AGB,∠GBF=∠GAB,
∴△BGF∽△AGB,
∴BG2=GF GA,
∴x2=(2﹣x)×2,
∴x2+2x﹣4=0,
∴x=﹣1+或﹣1﹣(舍弃),
∴FG=AG﹣AF=2﹣(﹣1+)=3﹣,
故选:A.
4.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
5.解:正五边形的内角=(5﹣2)×180°÷5=108°,
∴∠E=∠D=108°,
∵AE、CD分别与⊙O相切于A、C两点,
∴∠OAE=∠OCD=90°,
∴∠AOC=540°﹣90°﹣90°﹣108°﹣108°=144°,
故选:A.
6.解:如图所示,连接OE、OF,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠EOF=60°,
∵OE=OF,
∴△EOF是等边三角形,
∴∠OEM=60°,
∴OM=OE sin∠OEM,
∴OE==,
∵∠OEN=30°,
∴ON=OE=,EN=1.
∴CE=2EN=2.
∴S△ACE=.
故选:D.
7.解:由题意:每次的旋转角均为60°,
∵360°÷60°=6,
∴操作6次后,A6与A重合.
∵每次的旋转半径均为OA,
∴顺次连接点A、A1…A5形成的多边形是正六边形.
故选:C.
8.解:如图,连接OA,OC.
∵∠HOB=∠AOC=120°,∠OCH=∠OAG=60°,
∴∠HOC=∠GOA,
在△OHC和△OGA中,
,
∴△HOC≌△GOA(ASA),
∴AG=CH,
∴S阴=S四边形OABC=定值,l=GB+BC+CH=AG+BG+BC=2BC=定值,
故选:D.
9.解:如图所示:可得MN=BC=20cm,
△OWM是等边三角形,边长为10cm,
则它的高为:=5(cm),
故FG=20+4×5=(20+20)cm.
故选:C.
二.填空题(共5小题,满分20分)
10.解:如图,观察图象可知,直径为4的圆及其内部最多能覆盖住的格点个数为13个.
故答案为:13.
11.解:连接OA,OB,OC,OC1.
∵ABCDE是正五边形,
∴OA=OB=OC,∠ABC=108°,
∵C,C1关于PQ对称,
∴OC=OC1,
∴OA=OB=OC=OC1,
∴A,B,C,C1四点共圆,
∴∠ABC+∠CC1A=180°,
∴∠CC1A=72°,
故答案为:72.
12.解:在圆内接正六边形ABCDEF中,∠COD==60°,
∵OC=OD,
∴△OCD是等边三角形,
∴BC=CD=OC=4,
∵OG⊥BC,
∴CG=BC=2,
∵∠COG=∠COD=30°,
∴OG=CG=2,
故答案为:60°,4,2.
13.解:连接OB、OC,
正多边形的每个外角相等,且其和为360°,
据此可得多边形的边数为:=9,
∴∠AOB==40°,
∴∠AOD=40°×3=120°.
故答案为:120°
14.解:(1)连接BD.
∵∠BAD+∠BCD=180°,∠BCD=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵∠AED+∠ABD=180°,
∴∠AED=120°,
故答案为:120°
(2)连接OA.
∵∠EOD=90°,∠AOD=2∠ABD=120°,
∴∠AOE=∠AOD﹣∠EOD=30°,
∵AE恰好为⊙O的内接正n边形的一边,
∴n==12,
故答案为:12.
三.解答题(共9小题,满分64分)
15.证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.
(3)答:;
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=,
∴PM=PB,
∴
∴
16.解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
17.解:(1)设此圆的半径为R,
则它的内接正方形的边长为R,
它的内接正六边形的边长为R,
内接正方形和内接正六边形的边长比为R:R=:1.
故答案为::1;
(2)BE是⊙O的内接正十二边形的一边,
理由:连接OA,OB,OE,
在正方形ABCD中,∠AOB=90°,
在正六边形AEFCGH中,∠AOE=60°,
∴∠BOE=30°,
∵n==12,
∴BE是正十二边形的边.
18.(1)证明:如图1中,
∵五边形ABCDE是正五边形,
∴∠BCD=∠BAE=108°,
∵AB=AE,
∴∠ABE=∠AEB=36°,
∴∠CBE=72°,
∴∠DCB+∠CBE=180°,
∴CD∥BE,
同法可证,AC∥DE,
∴四边形PEDC是平行四边形,
∵CD=DE,
∴四边形PEDC是菱形;
(2)证明:如图2中,连接AN.
∵∠MCA=∠MAC=72°,
∴MC=MA,
∵BC=BA,
∴BM垂直平分线段AC,
∴NC=NA,
∴∠NCA=∠NAC=∠CEP=36°,
∵∠PAE=∠NEA=72°,
∴∠PEA=∠NAE=36°,
∵AE=EA,
∴△PAE≌△NEA,
∴AN=PE,
∴CN=PE.
(3)解:如图3中.在AD上取一点W,使得AW=WE.设AW=x.
∵∠A=∠D=∠AEW=36°,
∴∠DWE=∠DEW=72°,
∴DW=DE=2,
∵∠A=∠A,∠AEW=∠D,
∴△AWE∽△AED,
∴AE2=AW AD,
∴22=x(x+2),
解得x=﹣1,
∴AD=2+x=+1,
故答案为+1.
19.证明:∵∠A=∠B=∠C=∠D=∠E,∠A对着,∠B对着,
∴=,
∴﹣=﹣,即=,
∴BC=AE.
同理可证其余各边都相等,
∴五边形ABCDE是正五边形.
20.解:∵正六边形的半径等于边长,
∴正六边形的边长a=2cm;
正六边形的周长l=6a=12cm;
正六边形的面积S=6××2×=.
故答案为:2cm,12cm,6cm2.
21.解:如图设OF=x,
则BO=1﹣x,BC=1,AD=0.5,AO=1+x,
故BC2+BO2=AD2+AO2,
则可以列方程为
1+(1﹣x)2=(1+x)2+0.52,(两边都是圆半径的平方)
解上面的方程得,
x=;
所以能将其完全覆盖的圆的最小半径R2=1+(1﹣x)2
R=.
22.解:(1)在正六边形ABCDEF中,∠DAB=60°,
在正方形AQDP中,∠DAP=45°,
∴∠BAM=∠DAB﹣∠DAP=60°﹣45°=15°,
故答案为:15.
(2)连接BE交AD于点O,连接OP交BC于H.
在正六边形ABCDEF 中,CD=BC=AB=4,∠BAF=∠ABC=∠C=∠CDE=120°,
AO、BO 平分∠BAF、∠ABC,OA=OB,
∴∠BAO=∠ABO=∠CBO=×120°=60°,
∴△ABO 是等边三角形,
∴BC∥AD,AO=BO=AB=4,
∴AD=2AO=8,
在正方形APDQ 中,AP=DP,∠APD=90°,
∵AO=DO,
∴PO=AD=4,PO⊥AD,∠APO=∠DPO=∠APD=45°,
∵AD∥BC,
∴∠MHP=∠AOP=90°,
∴∠BHO=90°,
∴sin∠OBH=,
∵∠OBH=60°,BO=4,
∴OH=4×sin60°=2,
∵PH=MH=OP﹣OH=4﹣2,
∴MN=2MH=8﹣4≈1.1.
23.解:(1)连接OD,OC,
∵正方形ABCD内接于⊙O,
∴∠DOC=90°.
∴;
(2)连接PO,OB,
∵正方形ABCD内接于⊙O,
∴∠COB=90°,
∵点P为BC的中点,
∴=,
∴,
∴n=360÷45=8.
一.选择题(共9小题,满分36分)
1.如图,点A,B,C,D,E,F,G,H为⊙O的八等分点,AD与BH的交点为I,若⊙O的半径为1,则HI的长等于( )
A.2﹣ B.2+ C.2 D.
2.把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )
A.1 B.2 C. D.2
3.如图,在正五边形ABCDE中,连接AC,BE,BD,AC与BE,BD分别交于点F,G,若AB=2,则FG的长为( )
A.3﹣ B.﹣1 C. D.2﹣3
4.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3 B.:1 C.: D.1:
5.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( )
A.144° B.130° C.129° D.108°
6.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=1,则该圆的内接正三角形ACE的面积为( )
A.2 B.4 C. D.
7.线段OA以点O为旋转中心,逆时针旋转60°,得到OA1,再将OA1以点O为旋转中心逆时针旋转60°得到OA2,依此操作直到点An与点A重合为止,顺次连接点A、A1…An﹣1形成的多边形是( )
A.正四边形 B.正五边形 C.正六边形 D.正七边形
8.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
9.如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是( )
A.(20+10)cm B.(30+10)cm C.(20+20)cm D.40cm
二.填空题(共5小题,满分20分)
10.在每个小正方形的边长为1的网格中直径为4的圆及其内部最多能覆盖住的格点个数为 .
11.如图,直线PQ经过正五边形ABCDE的中心O,与AB、CD边分别交于点P、Q,点C1是点C关于直线PQ的对称点,连接CC1,AC1,则∠CC1A的度数为 °.
12.如图,在圆内接正六边形ABCDEF中,半径OC=4,OG⊥BC,垂足为点G,则正六边形的中心角= ,边长= ,边心距= .
13.如图,点A,B,C,D是一个外角为40°的正多边形的顶点,若O为正多边形的中心,则∠AOD的度数为 .
14.如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上,连接OD、OE、AE、DE.
(1)∠AED的度数为 ;
(2)当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,则n的值为 .
三.解答题(共9小题,满分64分)
15.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:;
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,并给予证明.
16.如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数是 ;图2中,∠APN的度数是 ,图3中∠APN的度数是 .
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
17.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.
(1)正方形ABCD与正六边形AEFCGH的边长之比为 ;
(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.
18.如图,正五边形ABCDE中.
(1)AC与BE相交于P,求证:四边形PEDC为菱形;
(2)延长DC、AE交于M点,连BM交CE于N,求证:CN=EP;
(3)若正五边形边长为2,直接写出AD的长为 .
19.如图五边形ABCDE内接于⊙O,∠A=∠B=∠C=∠D=∠E.求证:五边形ABCDE是正五边形.
20.已知正六边形ABCDEF的半径为2cm,求这个正六边形的边长、周长和面积.
21.如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.
22.如图,在正六边形ABCDEF中,以AD为对角线作正方形APDQ,AP、DP与BC分别交于M、N.
(1)∠BAM= °;
(2)若AB=4,求MN的长.(参考数据:≈1.73,结果精确到0.1,可以直接利用(1)的结论)
23.如图,正方形ABCD内接于⊙O,P为上的一点,连接DP,CP.
(1)求∠CPD的度数;
(2)当点P为的中点时,CP是⊙O的内接正n边形的一边,求n的值.
参考答案
一.选择题(共9小题,满分36分)
1.解:如图,连接AB、OH,作OM⊥AD于M,ON⊥BH于N,在IH上截取一点K,使得ON=NK,连接OK.
∵点A,B,C,D,E,F,G,H为⊙O的八等分点,
∴∠A=∠B=45°,∠H=22.5°,
∴∠AIB=90°,
∴∠MIN=∠OMI=∠ONI=90°,
∴四边形OMIN是矩形,
∵=,
∴AD=BH,
∴OM=ON,
∴四边形OMIN是正方形,设OM=a,
∵ON=NK,
∴∠OKN=45°,
∵∠OKN=∠H+∠KOH,
∴∠H=∠KOH=22.5°,
∴OK=KN=a,
在Rt△ONH中,a2+(a+a)2=1,
∴a=,
∴IH=(2+)a=.
故选:D.
2.解:如图,
∵重叠部分为正八边形的一半,
∴GF=EF=PE=HP,∠GFE=∠FEP=∠HPE=135°,
∴∠GFC=∠B'FE=∠DEP=∠A'PH=45°,
∴△CGF、△B'EF是全等的等腰直角三角形,
设CG=x,则GF=x,B'F=x,
∴BG=B'G=x+x,
∴BC=x+x+x=2+,
∴x=1,
∴GF=,
故选:C.
3.解:∵五边形ABCDE是正五边形,
∴∠BAF=∠ABF=∠DBE=36°,
∴FA=FB,
∴∠ABG=∠AGB=∠BFG=72°,
∴AB=AG=2,BG=BF,
设AF=BF=BG=x,
∵∠BGF=∠AGB,∠GBF=∠GAB,
∴△BGF∽△AGB,
∴BG2=GF GA,
∴x2=(2﹣x)×2,
∴x2+2x﹣4=0,
∴x=﹣1+或﹣1﹣(舍弃),
∴FG=AG﹣AF=2﹣(﹣1+)=3﹣,
故选:A.
4.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
5.解:正五边形的内角=(5﹣2)×180°÷5=108°,
∴∠E=∠D=108°,
∵AE、CD分别与⊙O相切于A、C两点,
∴∠OAE=∠OCD=90°,
∴∠AOC=540°﹣90°﹣90°﹣108°﹣108°=144°,
故选:A.
6.解:如图所示,连接OE、OF,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠EOF=60°,
∵OE=OF,
∴△EOF是等边三角形,
∴∠OEM=60°,
∴OM=OE sin∠OEM,
∴OE==,
∵∠OEN=30°,
∴ON=OE=,EN=1.
∴CE=2EN=2.
∴S△ACE=.
故选:D.
7.解:由题意:每次的旋转角均为60°,
∵360°÷60°=6,
∴操作6次后,A6与A重合.
∵每次的旋转半径均为OA,
∴顺次连接点A、A1…A5形成的多边形是正六边形.
故选:C.
8.解:如图,连接OA,OC.
∵∠HOB=∠AOC=120°,∠OCH=∠OAG=60°,
∴∠HOC=∠GOA,
在△OHC和△OGA中,
,
∴△HOC≌△GOA(ASA),
∴AG=CH,
∴S阴=S四边形OABC=定值,l=GB+BC+CH=AG+BG+BC=2BC=定值,
故选:D.
9.解:如图所示:可得MN=BC=20cm,
△OWM是等边三角形,边长为10cm,
则它的高为:=5(cm),
故FG=20+4×5=(20+20)cm.
故选:C.
二.填空题(共5小题,满分20分)
10.解:如图,观察图象可知,直径为4的圆及其内部最多能覆盖住的格点个数为13个.
故答案为:13.
11.解:连接OA,OB,OC,OC1.
∵ABCDE是正五边形,
∴OA=OB=OC,∠ABC=108°,
∵C,C1关于PQ对称,
∴OC=OC1,
∴OA=OB=OC=OC1,
∴A,B,C,C1四点共圆,
∴∠ABC+∠CC1A=180°,
∴∠CC1A=72°,
故答案为:72.
12.解:在圆内接正六边形ABCDEF中,∠COD==60°,
∵OC=OD,
∴△OCD是等边三角形,
∴BC=CD=OC=4,
∵OG⊥BC,
∴CG=BC=2,
∵∠COG=∠COD=30°,
∴OG=CG=2,
故答案为:60°,4,2.
13.解:连接OB、OC,
正多边形的每个外角相等,且其和为360°,
据此可得多边形的边数为:=9,
∴∠AOB==40°,
∴∠AOD=40°×3=120°.
故答案为:120°
14.解:(1)连接BD.
∵∠BAD+∠BCD=180°,∠BCD=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵∠AED+∠ABD=180°,
∴∠AED=120°,
故答案为:120°
(2)连接OA.
∵∠EOD=90°,∠AOD=2∠ABD=120°,
∴∠AOE=∠AOD﹣∠EOD=30°,
∵AE恰好为⊙O的内接正n边形的一边,
∴n==12,
故答案为:12.
三.解答题(共9小题,满分64分)
15.证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.
(3)答:;
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=,
∴PM=PB,
∴
∴
16.解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
17.解:(1)设此圆的半径为R,
则它的内接正方形的边长为R,
它的内接正六边形的边长为R,
内接正方形和内接正六边形的边长比为R:R=:1.
故答案为::1;
(2)BE是⊙O的内接正十二边形的一边,
理由:连接OA,OB,OE,
在正方形ABCD中,∠AOB=90°,
在正六边形AEFCGH中,∠AOE=60°,
∴∠BOE=30°,
∵n==12,
∴BE是正十二边形的边.
18.(1)证明:如图1中,
∵五边形ABCDE是正五边形,
∴∠BCD=∠BAE=108°,
∵AB=AE,
∴∠ABE=∠AEB=36°,
∴∠CBE=72°,
∴∠DCB+∠CBE=180°,
∴CD∥BE,
同法可证,AC∥DE,
∴四边形PEDC是平行四边形,
∵CD=DE,
∴四边形PEDC是菱形;
(2)证明:如图2中,连接AN.
∵∠MCA=∠MAC=72°,
∴MC=MA,
∵BC=BA,
∴BM垂直平分线段AC,
∴NC=NA,
∴∠NCA=∠NAC=∠CEP=36°,
∵∠PAE=∠NEA=72°,
∴∠PEA=∠NAE=36°,
∵AE=EA,
∴△PAE≌△NEA,
∴AN=PE,
∴CN=PE.
(3)解:如图3中.在AD上取一点W,使得AW=WE.设AW=x.
∵∠A=∠D=∠AEW=36°,
∴∠DWE=∠DEW=72°,
∴DW=DE=2,
∵∠A=∠A,∠AEW=∠D,
∴△AWE∽△AED,
∴AE2=AW AD,
∴22=x(x+2),
解得x=﹣1,
∴AD=2+x=+1,
故答案为+1.
19.证明:∵∠A=∠B=∠C=∠D=∠E,∠A对着,∠B对着,
∴=,
∴﹣=﹣,即=,
∴BC=AE.
同理可证其余各边都相等,
∴五边形ABCDE是正五边形.
20.解:∵正六边形的半径等于边长,
∴正六边形的边长a=2cm;
正六边形的周长l=6a=12cm;
正六边形的面积S=6××2×=.
故答案为:2cm,12cm,6cm2.
21.解:如图设OF=x,
则BO=1﹣x,BC=1,AD=0.5,AO=1+x,
故BC2+BO2=AD2+AO2,
则可以列方程为
1+(1﹣x)2=(1+x)2+0.52,(两边都是圆半径的平方)
解上面的方程得,
x=;
所以能将其完全覆盖的圆的最小半径R2=1+(1﹣x)2
R=.
22.解:(1)在正六边形ABCDEF中,∠DAB=60°,
在正方形AQDP中,∠DAP=45°,
∴∠BAM=∠DAB﹣∠DAP=60°﹣45°=15°,
故答案为:15.
(2)连接BE交AD于点O,连接OP交BC于H.
在正六边形ABCDEF 中,CD=BC=AB=4,∠BAF=∠ABC=∠C=∠CDE=120°,
AO、BO 平分∠BAF、∠ABC,OA=OB,
∴∠BAO=∠ABO=∠CBO=×120°=60°,
∴△ABO 是等边三角形,
∴BC∥AD,AO=BO=AB=4,
∴AD=2AO=8,
在正方形APDQ 中,AP=DP,∠APD=90°,
∵AO=DO,
∴PO=AD=4,PO⊥AD,∠APO=∠DPO=∠APD=45°,
∵AD∥BC,
∴∠MHP=∠AOP=90°,
∴∠BHO=90°,
∴sin∠OBH=,
∵∠OBH=60°,BO=4,
∴OH=4×sin60°=2,
∵PH=MH=OP﹣OH=4﹣2,
∴MN=2MH=8﹣4≈1.1.
23.解:(1)连接OD,OC,
∵正方形ABCD内接于⊙O,
∴∠DOC=90°.
∴;
(2)连接PO,OB,
∵正方形ABCD内接于⊙O,
∴∠COB=90°,
∵点P为BC的中点,
∴=,
∴,
∴n=360÷45=8.
