2021-2022学年鲁教版(五四制)九年级数学下册5.9弧长及扇形的面积 同步达标训练(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.9弧长及扇形的面积 同步达标训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 230.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 07:22:29 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学下册《5.9弧长及扇形的面积》同步达标训练(附答案)
1.在半径为3的圆中,150°的圆心角所对的弧长是( )
A. B. C. D.
2.如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
A. B. C. D.
3.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧的长等于( )
A. B. C. D.
4.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则劣弧的长为( )
A.π B. C.2π D.3π
5.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若∠ACB=60°,则劣弧AB的长是( )
A.8πcm B.16πcm C.32πcm D.192πcm
6.如图,CD为⊙O的弦,直径AB为4,AB⊥CD于E,∠A=30°,则扇形BOC的面积为( )
A. B. C.π D.
7.已知一个扇形的半径是12,圆心角是60°,则这个扇形的面积是( )
A.32π B.24π C.12π D.8π
8.扇形的弧长为10πcm,面积为120πcm2,则扇形的半径是( )
A.12cm B.24cm C.28cm D.30cm
9.如图,正方形ABCD内接于圆O,AB=4,则图中阴影部分的面积是( )
A.4π﹣16 B.8π﹣16 C.16π﹣32 D.32π﹣16
10.如图点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A.π﹣4 B. C.π﹣2 D.
11.若扇形的半径为3,圆心角120°,为则此扇形的弧长是 .
12.在半径为6的⊙O中,120°的圆心角所对的弧长是 .
13.一个扇形的圆心角是120°.它的半径是3cm.则扇形的弧长为 cm.
14.如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则的长为 .
15.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长 .
16.如图,⊙O的半径为3,点A,B,C,D都在⊙O上,∠AOB=30°,将扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,则的长为 .(结果保留π)
17.已知扇形的半径为3,圆心角为120°,则该扇形的弧长是 ,面积等于 .(结果保留π)
18.已知扇形的半径为4cm,圆心角为270°,则扇形的面积为 .
19.已知扇形的面积为12π,半径等于6,则它的圆心角等于 度.
20.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角是 度.
21.如图,半圆O的直径AE=4,弦AB=BC,弦CD=DE,连接OB,OD,则图中两个阴影部分的面积和为 .
22.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为 .
23.圆O的半径为3,弧AB的所对的圆心角为60度.
(1)求圆弧AB所在的扇形面积.
(2)求弦AB所对的弧长.
24.如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系,若△AOB绕点O逆时针旋转90°后,得到△A1OB1(A和A1是对应点)
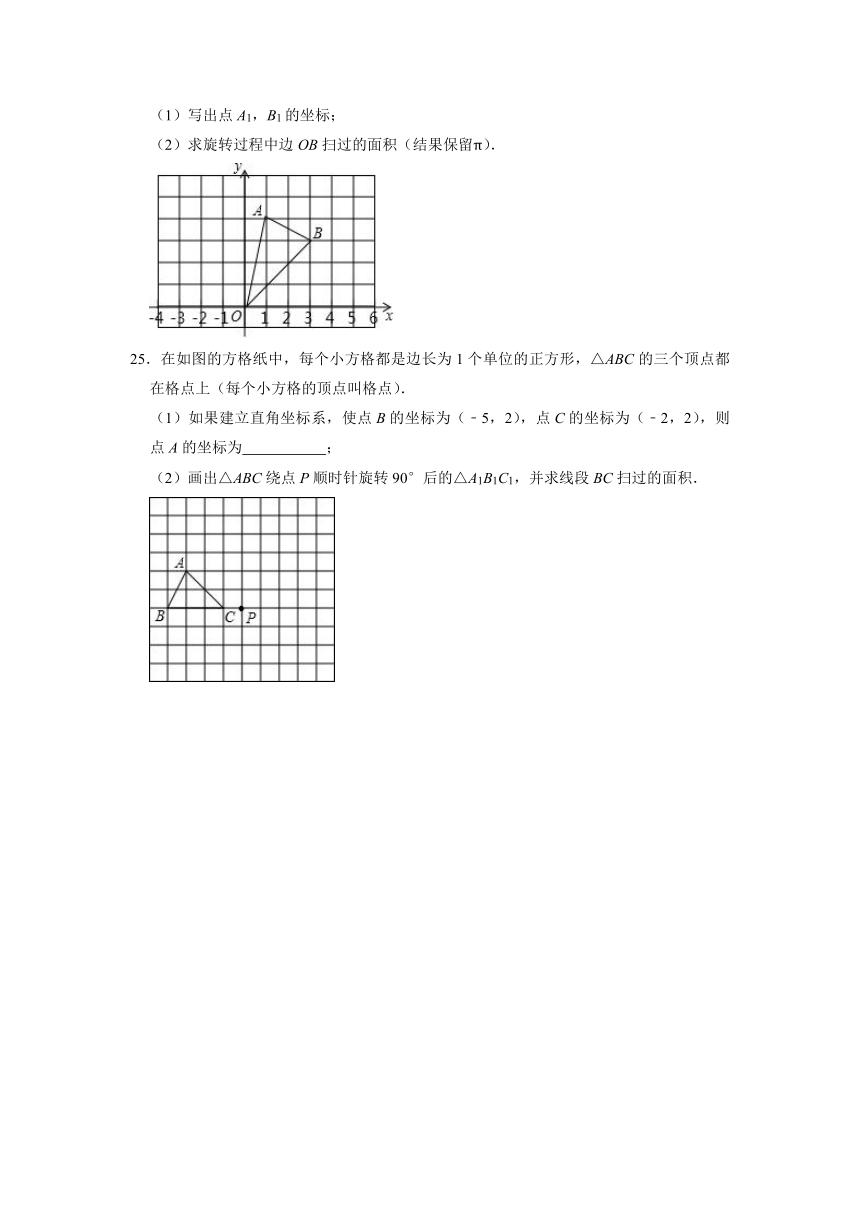
(1)写出点A1,B1的坐标;
(2)求旋转过程中边OB扫过的面积(结果保留π).
25.在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
(1)如果建立直角坐标系,使点B的坐标为(﹣5,2),点C的坐标为(﹣2,2),则点A的坐标为 ;
(2)画出△ABC绕点P顺时针旋转90°后的△A1B1C1,并求线段BC扫过的面积.
参考答案
1.解:=.
故选:D.
2.解:连接OB,OC.
∠BOC=2∠BAC=2×36°=72°,
则劣弧BC的长是:=π.
故选:B.
3.解:如图,连接OB、OC,
∵∠BAC=30°,
∴∠BOC=2∠BAC=60°,
又OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴劣弧的长为:=.
故选:A.
4.解:∵四边形ABCD内接于⊙O,
∴∠BCD+∠A=180°,
∵∠BOD=2∠A,∠BOD=∠BCD,
∴2∠A+∠A=180°,
解得:∠A=60°,
∴∠BOD=120°,
∴的长==2π;
故选:C.
5.解:由题意得:CA和CB分别与⊙O相切于点A和点B,
∴OA⊥CA,OB⊥CB,
∴∠OAC=∠OBC=90°,
∵∠ACB=60°,
∴∠AOB=120°,
∴=16π(cm),
故选:B.
6.解:连接AC,
∵CD为⊙O的弦,AB是⊙O的直径,
∴CE=DE,
∵AB⊥CD,
∴AC=AD,
∴∠CAB=∠DAB=30°,
∴∠COB=60°,
∴扇形BOC的面积==,
故选:B.
7.解:这个扇形的面积为=24π,
故选:B.
8.解:∵S扇形=lr,
∴120π= 10π r,
∴r=24(cm);
故选:B.
9.解:连接OA、OB,
∵四边形ABCD是正方形,
∴∠AOB=90°,∠OAB=45°,
∴OA=ABcos45°=4×=2,
所以阴影部分的面积=S⊙O﹣S正方形ABCD=π×(2)2﹣4×4=8π﹣16.
故选:B.
10.解:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴S阴影=S扇形OBC﹣S△OBC=﹣×2×2=π﹣2,
故选:C.
11.解:∵扇形的半径为3,圆心角为120°,
∴此扇形的弧长==2π.
故答案为:2π
12.解:根据弧长的公式l=,
得到:l==4π.
13.解:根据题意,扇形的弧长为=2π,
故答案为:2π
14.解:连接OB,OC,
∵∠A=60°,
∴∠BOC=120°,
则===4π.
故答案为:4π.
15.解:连接OA、OC,
∵∠B=135°,
∴∠D=180°﹣135°=45°,
∴∠AOC=90°,
则的长==π.
故答案为:π.
16.解:∵扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,
∴∠BOD=120°,
∴∠AOD=∠AOB+∠BOD=30°+120°=150°,
∴的长==π.
故答案为π.
17.解:扇形的弧长==2π;
扇形的面积==3π.
故答案为:2π,3π.
18.解:∵扇形的半径为4cm,圆心角为270°,
∴扇形的面积是:=12π(cm2).
故填:12πcm2.
19.解:根据扇形的面积公式,得
n===120°.
故答案为:120.
20.解:扇形的面积公式=lr=240πcm2,
解得:r=24cm,
又∵l==20πcm,
∴n=150°.
故答案为:150.
21.解:如图,∵弦AB=BC,弦CD=DE,
∴=,=,
∴+=+
∴∠BOD=90°,
∴S阴影=S扇形OBD==π.
故答案是:π.
22.解:∵半圆绕点B顺时针旋转45°,点A旋转到A′的位置,
∴S半圆AB=S半圆A′B,∠ABA′=45°,
∴S阴影部分+S半圆AB=S半圆A′B,+S扇形ABA′,
∴S阴影部分=S扇形ABA′==2π.
故答案为2π.
23.解:(1)圆弧AB所在的扇形面积==;
(2)弦AB所对的劣弧长==π.弦AB所对的优弧长=6π﹣π=5π.
答:(1)圆弧AB所在的扇形面积是;
(2)弦AB所对的弧长是π或5π.
24.解:(1)如图,△A1OB1为所作;
所以点A1的坐标为(﹣4,1),点B1的坐标为(﹣3,3)
(2)OB=,
所以旋转过程中边OB扫过的面积=.
25.解:(1)观察A、B的位置知:将B点向右平移1个单位,再向上平移2个单位,可得A点坐标;故:A(﹣4,4).(2分)
(2)如图;
线段BC扫过的面积=(42﹣12)=.
1.在半径为3的圆中,150°的圆心角所对的弧长是( )
A. B. C. D.
2.如图,⊙O的半径为1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是( )
A. B. C. D.
3.如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧的长等于( )
A. B. C. D.
4.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则劣弧的长为( )
A.π B. C.2π D.3π
5.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若∠ACB=60°,则劣弧AB的长是( )
A.8πcm B.16πcm C.32πcm D.192πcm
6.如图,CD为⊙O的弦,直径AB为4,AB⊥CD于E,∠A=30°,则扇形BOC的面积为( )
A. B. C.π D.
7.已知一个扇形的半径是12,圆心角是60°,则这个扇形的面积是( )
A.32π B.24π C.12π D.8π
8.扇形的弧长为10πcm,面积为120πcm2,则扇形的半径是( )
A.12cm B.24cm C.28cm D.30cm
9.如图,正方形ABCD内接于圆O,AB=4,则图中阴影部分的面积是( )
A.4π﹣16 B.8π﹣16 C.16π﹣32 D.32π﹣16
10.如图点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A.π﹣4 B. C.π﹣2 D.
11.若扇形的半径为3,圆心角120°,为则此扇形的弧长是 .
12.在半径为6的⊙O中,120°的圆心角所对的弧长是 .
13.一个扇形的圆心角是120°.它的半径是3cm.则扇形的弧长为 cm.
14.如图,△ABC内接于⊙O,若⊙O的半径为6,∠A=60°,则的长为 .
15.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长 .
16.如图,⊙O的半径为3,点A,B,C,D都在⊙O上,∠AOB=30°,将扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,则的长为 .(结果保留π)
17.已知扇形的半径为3,圆心角为120°,则该扇形的弧长是 ,面积等于 .(结果保留π)
18.已知扇形的半径为4cm,圆心角为270°,则扇形的面积为 .
19.已知扇形的面积为12π,半径等于6,则它的圆心角等于 度.
20.一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角是 度.
21.如图,半圆O的直径AE=4,弦AB=BC,弦CD=DE,连接OB,OD,则图中两个阴影部分的面积和为 .
22.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为 .
23.圆O的半径为3,弧AB的所对的圆心角为60度.
(1)求圆弧AB所在的扇形面积.
(2)求弦AB所对的弧长.
24.如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系,若△AOB绕点O逆时针旋转90°后,得到△A1OB1(A和A1是对应点)
(1)写出点A1,B1的坐标;
(2)求旋转过程中边OB扫过的面积(结果保留π).
25.在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
(1)如果建立直角坐标系,使点B的坐标为(﹣5,2),点C的坐标为(﹣2,2),则点A的坐标为 ;
(2)画出△ABC绕点P顺时针旋转90°后的△A1B1C1,并求线段BC扫过的面积.
参考答案
1.解:=.
故选:D.
2.解:连接OB,OC.
∠BOC=2∠BAC=2×36°=72°,
则劣弧BC的长是:=π.
故选:B.
3.解:如图,连接OB、OC,
∵∠BAC=30°,
∴∠BOC=2∠BAC=60°,
又OB=OC,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴劣弧的长为:=.
故选:A.
4.解:∵四边形ABCD内接于⊙O,
∴∠BCD+∠A=180°,
∵∠BOD=2∠A,∠BOD=∠BCD,
∴2∠A+∠A=180°,
解得:∠A=60°,
∴∠BOD=120°,
∴的长==2π;
故选:C.
5.解:由题意得:CA和CB分别与⊙O相切于点A和点B,
∴OA⊥CA,OB⊥CB,
∴∠OAC=∠OBC=90°,
∵∠ACB=60°,
∴∠AOB=120°,
∴=16π(cm),
故选:B.
6.解:连接AC,
∵CD为⊙O的弦,AB是⊙O的直径,
∴CE=DE,
∵AB⊥CD,
∴AC=AD,
∴∠CAB=∠DAB=30°,
∴∠COB=60°,
∴扇形BOC的面积==,
故选:B.
7.解:这个扇形的面积为=24π,
故选:B.
8.解:∵S扇形=lr,
∴120π= 10π r,
∴r=24(cm);
故选:B.
9.解:连接OA、OB,
∵四边形ABCD是正方形,
∴∠AOB=90°,∠OAB=45°,
∴OA=ABcos45°=4×=2,
所以阴影部分的面积=S⊙O﹣S正方形ABCD=π×(2)2﹣4×4=8π﹣16.
故选:B.
10.解:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴S阴影=S扇形OBC﹣S△OBC=﹣×2×2=π﹣2,
故选:C.
11.解:∵扇形的半径为3,圆心角为120°,
∴此扇形的弧长==2π.
故答案为:2π
12.解:根据弧长的公式l=,
得到:l==4π.
13.解:根据题意,扇形的弧长为=2π,
故答案为:2π
14.解:连接OB,OC,
∵∠A=60°,
∴∠BOC=120°,
则===4π.
故答案为:4π.
15.解:连接OA、OC,
∵∠B=135°,
∴∠D=180°﹣135°=45°,
∴∠AOC=90°,
则的长==π.
故答案为:π.
16.解:∵扇形AOB绕点O顺时针旋转120°后恰好与扇形COD重合,
∴∠BOD=120°,
∴∠AOD=∠AOB+∠BOD=30°+120°=150°,
∴的长==π.
故答案为π.
17.解:扇形的弧长==2π;
扇形的面积==3π.
故答案为:2π,3π.
18.解:∵扇形的半径为4cm,圆心角为270°,
∴扇形的面积是:=12π(cm2).
故填:12πcm2.
19.解:根据扇形的面积公式,得
n===120°.
故答案为:120.
20.解:扇形的面积公式=lr=240πcm2,
解得:r=24cm,
又∵l==20πcm,
∴n=150°.
故答案为:150.
21.解:如图,∵弦AB=BC,弦CD=DE,
∴=,=,
∴+=+
∴∠BOD=90°,
∴S阴影=S扇形OBD==π.
故答案是:π.
22.解:∵半圆绕点B顺时针旋转45°,点A旋转到A′的位置,
∴S半圆AB=S半圆A′B,∠ABA′=45°,
∴S阴影部分+S半圆AB=S半圆A′B,+S扇形ABA′,
∴S阴影部分=S扇形ABA′==2π.
故答案为2π.
23.解:(1)圆弧AB所在的扇形面积==;
(2)弦AB所对的劣弧长==π.弦AB所对的优弧长=6π﹣π=5π.
答:(1)圆弧AB所在的扇形面积是;
(2)弦AB所对的弧长是π或5π.
24.解:(1)如图,△A1OB1为所作;
所以点A1的坐标为(﹣4,1),点B1的坐标为(﹣3,3)
(2)OB=,
所以旋转过程中边OB扫过的面积=.
25.解:(1)观察A、B的位置知:将B点向右平移1个单位,再向上平移2个单位,可得A点坐标;故:A(﹣4,4).(2分)
(2)如图;
线段BC扫过的面积=(42﹣12)=.
