沪科版 2021-2022学年八年级数学上册11.1 平面内点的坐标 同步测试卷(word版、含答案)
文档属性
| 名称 | 沪科版 2021-2022学年八年级数学上册11.1 平面内点的坐标 同步测试卷(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 176.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览


文档简介
11.1 平面内点的坐标同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
在平面直角坐标系中,对于坐标P(2,5),下列说法错误的是( )
A. 表示这个点在平面内的位置
B. 点的纵坐标是
C. 点到轴的距离是
D. 它与点表示同一个坐标
点P到x轴的距离是2,到y轴的距离是3,且点P在y轴的右侧,则点P的坐标是( )
A. B. 或
C. D. 或
点在第四象限,且,那么点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
已知点P(0,a)在y轴的正半轴上,则点Q(--1,a+1)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
在平面直角坐标系中,点P(x,y)经过某种变换后得到点P'(-y+1,x+2),我们把点P'(-y+1,x+2)叫做点P(x,y)的终结点.已知点的终结点为,点的终结点为,点的终结点为这样依次得到点,,,,,.若点的坐标为(2,0),则点的坐标为( )
A. B. C. D.
已知点A(-3,0)和点B(2,0),则线段AB的长为( )
A. B. C. D.
已知过A(-1,a),B(2,-2)两点的直线平行于x轴,则a的值为( )
A. B. C. D.
点A(-5,4),B在平面直角坐标系中,且ABy轴.若三角形ABO的面积为5,则点B的坐标为( )
A. B.
C. D. 或
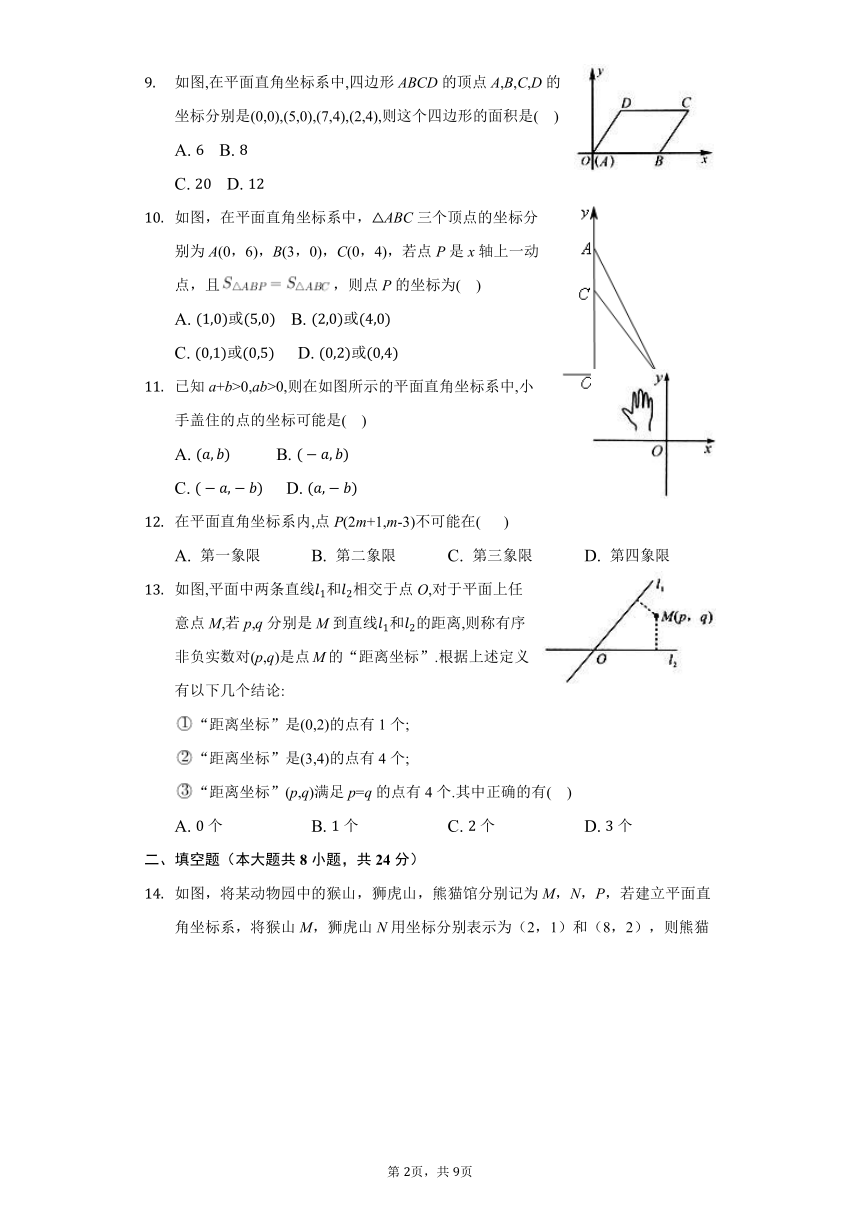
如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4),则这个四边形的面积是( )
A. B.
C. D.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,6),B(3,0),C(0,4),若点P是x轴上一动点,且,则点P的坐标为( )
A. 或 B. 或
C. 或 D. 或
已知a+b>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A. B.
C. D.
在平面直角坐标系内,点P(2m+1,m-3)不可能在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
如图,平面中两条直线和相交于点O,对于平面上任意点M,若p,q分别是M到直线和的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.根据上述定义,有以下几个结论:
“距离坐标”是(0,2)的点有1个;
“距离坐标”是(3,4)的点有4个;
“距离坐标”(p,q)满足p=q的点有4个.其中正确的有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共8小题,共24分)
如图,将某动物园中的猴山,狮虎山,熊猫馆分别记为M,N,P,若建立平面直角坐标系,将猴山M,狮虎山N用坐标分别表示为(2,1)和(8,2),则熊猫馆P用坐标表示为______.
若点P在第二、四象限的角平分线上,则a= .
如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”F到y轴的距离为2,则点F的坐标为 .
在平面直角坐标系中,一个四边形各顶点坐标分别为A(-1,-2),B(4,-2),C(4,3),D(-1,3),则四边形ABCD的形状是 .
在平面直角坐标系中,若点M(-2,a)与点N(x,a)之间的距离是2,则x的值是 .
长方形ABCD的边AB=4,BC=6,若将该长方形放在平面直角坐标系中,使点A的坐标为(-1,2),点B的坐标为(3,2),则点C的坐标是 .
已知点P(2a+5,10-3a)位于两坐标轴所成角的平分线上,则点P的坐标为 .
如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(4,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒的速度匀速运动,物体乙按顺时针方向以2个单位/秒的速度匀速运动,则两个物体运动后的第2021次相遇地点的坐标是 .
三、解答题(本大题共5小题,共57分)
已知点P(8-2m,m-1).
(1)若点P在x轴上,求m的值;
(2)若点P到两坐标轴的距离相等,求点P的坐标.
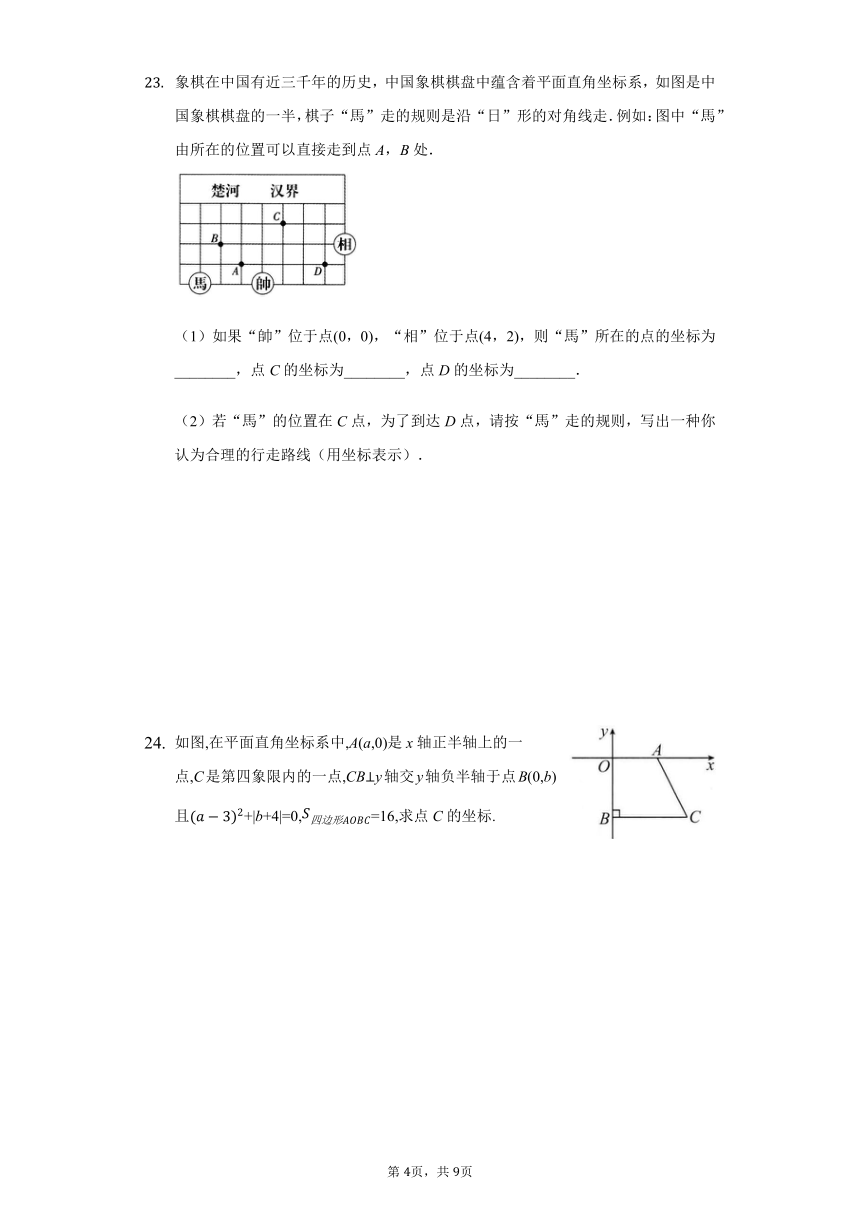
象棋在中国有近三千年的历史,中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“馬”走的规则是沿“日”形的对角线走.例如:图中“馬”由所在的位置可以直接走到点A,B处.
(1)如果“帥”位于点(0,0),“相”位于点(4,2),则“馬”所在的点的坐标为________,点C的坐标为________,点D的坐标为________.
(2)若“馬”的位置在C点,为了到达D点,请按“馬”走的规则,写出一种你认为合理的行走路线(用坐标表示).
如图,在平面直角坐标系中,A(a,0)是x轴正半轴上的一点,C是第四象限内的一点,CBy轴交y轴负半轴于点B(0,b),且+|b+4|=0,=16,求点C的坐标.
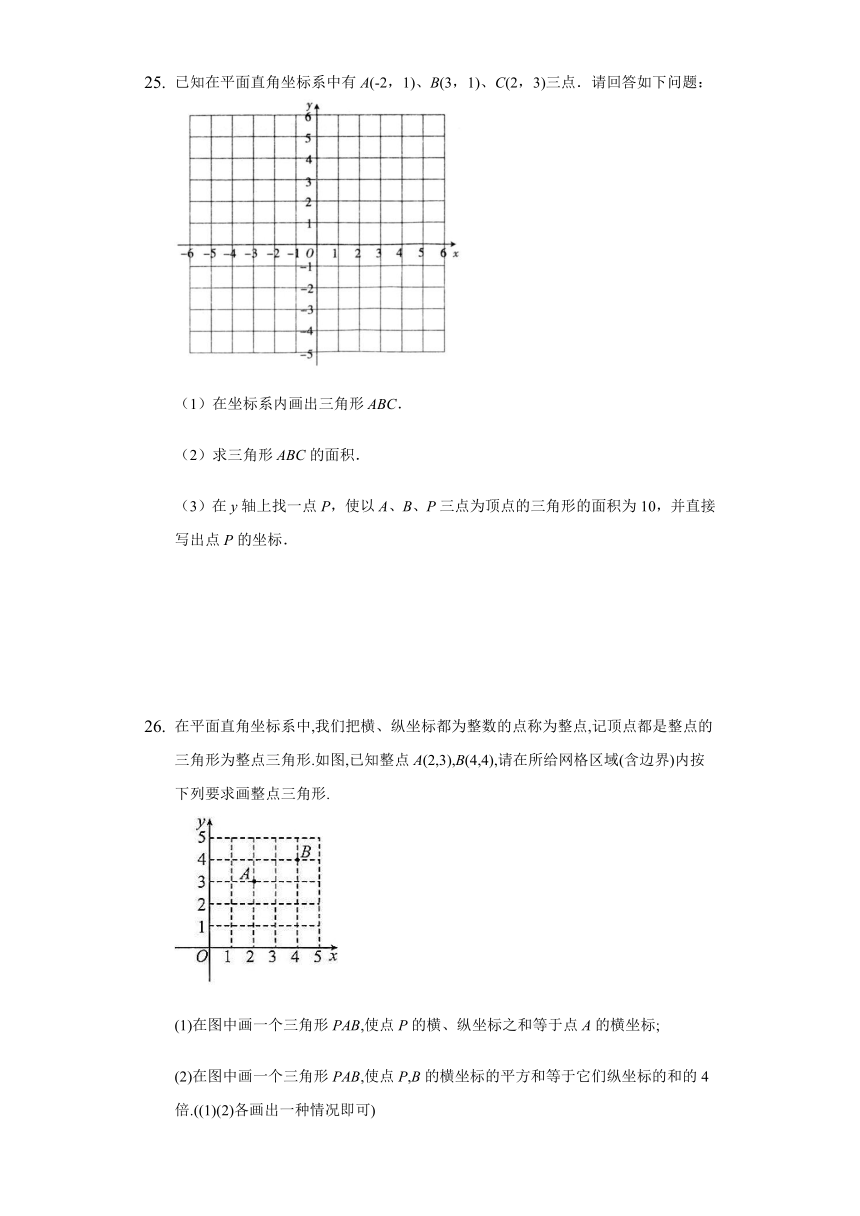
已知在平面直角坐标系中有A(-2,1)、B(3,1)、C(2,3)三点.请回答如下问题:
(1)在坐标系内画出三角形ABC.
(2)求三角形ABC的面积.
(3)在y轴上找一点P,使以A、B、P三点为顶点的三角形的面积为10,并直接写出点P的坐标.
在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)内按下列要求画整点三角形.
(1)在图中画一个三角形PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图中画一个三角形PAB,使点P,B的横坐标的平方和等于它们纵坐标的和的4倍.((1)(2)各画出一种情况即可)
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】B
12.【答案】B
13.【答案】B
14.【答案】(6,6)
15.【答案】-
16.【答案】(2,2)或
17.【答案】正方形
18.【答案】-4或0
19.【答案】(3,-4)或(3,8)
20.【答案】(7,7)或(35,-35)
21.【答案】(-2,-2)
22.【答案】解:(1)P点在X轴上,Y=0,
所以m-1=0,即m=1.
(2)P点到两轴的距离相等,
即8-2m=m-1,或8-2m=-(m-1),
即P(2,2)或(-6,6).
23.【答案】(1)(-3,0);(1,3); (3,1)
(2)如图,由(1,3)→(3,4)→(2,2)→(1,0)→(3,1)
24.【答案】解:因为+|b+4|=0,
所以a-3=0,b+4=0,
解得a=3,b=-4.
所以点A(3,0),B(0,-4).
所以OA=3,OB=4.
因为=16,
所以(OA+CB)OB=16,
所以(3+CB)4=16,解得CB=5.
因为点C在第四象限,且CBy轴,所以点C的坐标为(5,-4).
25.【答案】解:(1)描点如图;
(2)依题意,得AB∥x轴,且AB=3-(-2)=5,
∴S△ABC=×5×2=5;
(3)存在;
∵AB=5,S△ABP=10,
∴P点到AB的距离为4,
又点P在y轴上,
∴P点的坐标为(0,5)或(0,-3).
26.【答案】解:答案不唯一.
(1)三角形PAB如图所示.
(2)三角形PAB如图所示.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
在平面直角坐标系中,对于坐标P(2,5),下列说法错误的是( )
A. 表示这个点在平面内的位置
B. 点的纵坐标是
C. 点到轴的距离是
D. 它与点表示同一个坐标
点P到x轴的距离是2,到y轴的距离是3,且点P在y轴的右侧,则点P的坐标是( )
A. B. 或
C. D. 或
点在第四象限,且,那么点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
已知点P(0,a)在y轴的正半轴上,则点Q(--1,a+1)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
在平面直角坐标系中,点P(x,y)经过某种变换后得到点P'(-y+1,x+2),我们把点P'(-y+1,x+2)叫做点P(x,y)的终结点.已知点的终结点为,点的终结点为,点的终结点为这样依次得到点,,,,,.若点的坐标为(2,0),则点的坐标为( )
A. B. C. D.
已知点A(-3,0)和点B(2,0),则线段AB的长为( )
A. B. C. D.
已知过A(-1,a),B(2,-2)两点的直线平行于x轴,则a的值为( )
A. B. C. D.
点A(-5,4),B在平面直角坐标系中,且ABy轴.若三角形ABO的面积为5,则点B的坐标为( )
A. B.
C. D. 或
如图,在平面直角坐标系中,四边形ABCD的顶点A,B,C,D的坐标分别是(0,0),(5,0),(7,4),(2,4),则这个四边形的面积是( )
A. B.
C. D.
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,6),B(3,0),C(0,4),若点P是x轴上一动点,且,则点P的坐标为( )
A. 或 B. 或
C. 或 D. 或
已知a+b>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是( )
A. B.
C. D.
在平面直角坐标系内,点P(2m+1,m-3)不可能在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
如图,平面中两条直线和相交于点O,对于平面上任意点M,若p,q分别是M到直线和的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.根据上述定义,有以下几个结论:
“距离坐标”是(0,2)的点有1个;
“距离坐标”是(3,4)的点有4个;
“距离坐标”(p,q)满足p=q的点有4个.其中正确的有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共8小题,共24分)
如图,将某动物园中的猴山,狮虎山,熊猫馆分别记为M,N,P,若建立平面直角坐标系,将猴山M,狮虎山N用坐标分别表示为(2,1)和(8,2),则熊猫馆P用坐标表示为______.
若点P在第二、四象限的角平分线上,则a= .
如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”F到y轴的距离为2,则点F的坐标为 .
在平面直角坐标系中,一个四边形各顶点坐标分别为A(-1,-2),B(4,-2),C(4,3),D(-1,3),则四边形ABCD的形状是 .
在平面直角坐标系中,若点M(-2,a)与点N(x,a)之间的距离是2,则x的值是 .
长方形ABCD的边AB=4,BC=6,若将该长方形放在平面直角坐标系中,使点A的坐标为(-1,2),点B的坐标为(3,2),则点C的坐标是 .
已知点P(2a+5,10-3a)位于两坐标轴所成角的平分线上,则点P的坐标为 .
如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点A(4,0)同时出发,沿长方形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒的速度匀速运动,物体乙按顺时针方向以2个单位/秒的速度匀速运动,则两个物体运动后的第2021次相遇地点的坐标是 .
三、解答题(本大题共5小题,共57分)
已知点P(8-2m,m-1).
(1)若点P在x轴上,求m的值;
(2)若点P到两坐标轴的距离相等,求点P的坐标.
象棋在中国有近三千年的历史,中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“馬”走的规则是沿“日”形的对角线走.例如:图中“馬”由所在的位置可以直接走到点A,B处.
(1)如果“帥”位于点(0,0),“相”位于点(4,2),则“馬”所在的点的坐标为________,点C的坐标为________,点D的坐标为________.
(2)若“馬”的位置在C点,为了到达D点,请按“馬”走的规则,写出一种你认为合理的行走路线(用坐标表示).
如图,在平面直角坐标系中,A(a,0)是x轴正半轴上的一点,C是第四象限内的一点,CBy轴交y轴负半轴于点B(0,b),且+|b+4|=0,=16,求点C的坐标.
已知在平面直角坐标系中有A(-2,1)、B(3,1)、C(2,3)三点.请回答如下问题:
(1)在坐标系内画出三角形ABC.
(2)求三角形ABC的面积.
(3)在y轴上找一点P,使以A、B、P三点为顶点的三角形的面积为10,并直接写出点P的坐标.
在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)内按下列要求画整点三角形.
(1)在图中画一个三角形PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图中画一个三角形PAB,使点P,B的横坐标的平方和等于它们纵坐标的和的4倍.((1)(2)各画出一种情况即可)
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】B
12.【答案】B
13.【答案】B
14.【答案】(6,6)
15.【答案】-
16.【答案】(2,2)或
17.【答案】正方形
18.【答案】-4或0
19.【答案】(3,-4)或(3,8)
20.【答案】(7,7)或(35,-35)
21.【答案】(-2,-2)
22.【答案】解:(1)P点在X轴上,Y=0,
所以m-1=0,即m=1.
(2)P点到两轴的距离相等,
即8-2m=m-1,或8-2m=-(m-1),
即P(2,2)或(-6,6).
23.【答案】(1)(-3,0);(1,3); (3,1)
(2)如图,由(1,3)→(3,4)→(2,2)→(1,0)→(3,1)
24.【答案】解:因为+|b+4|=0,
所以a-3=0,b+4=0,
解得a=3,b=-4.
所以点A(3,0),B(0,-4).
所以OA=3,OB=4.
因为=16,
所以(OA+CB)OB=16,
所以(3+CB)4=16,解得CB=5.
因为点C在第四象限,且CBy轴,所以点C的坐标为(5,-4).
25.【答案】解:(1)描点如图;
(2)依题意,得AB∥x轴,且AB=3-(-2)=5,
∴S△ABC=×5×2=5;
(3)存在;
∵AB=5,S△ABP=10,
∴P点到AB的距离为4,
又点P在y轴上,
∴P点的坐标为(0,5)或(0,-3).
26.【答案】解:答案不唯一.
(1)三角形PAB如图所示.
(2)三角形PAB如图所示.
第2页,共2页
