沪科版2021-2022学年八年级数学上册11.2 图形在坐标系中的平移 同步测试卷 (word版、含答案)
文档属性
| 名称 | 沪科版2021-2022学年八年级数学上册11.2 图形在坐标系中的平移 同步测试卷 (word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 195.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 06:56:46 | ||
图片预览



文档简介
11.2 图形在坐标系中的平移同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共5小题,共25分)
在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P'的坐标为( )
A. B. C. D.
ABC的顶点A的坐标为(-2,5),若将ABC沿x轴平移5个单位长度,则A点坐标变为( )
A. B. 或
C. 或 D. 或
如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点(-2,2)处,则点B的对应点的坐标为( )
A. B.
C. D.
在平面直角坐标系中,线段CF是由线段AB平移得到的,点A(-2,3)的对应点为C(1,2),则点B(a,b)的对应点F的坐标为( )
A. B. C. D.
将三角形ABC平移得到三角形,若点A(m,n)和点(2m,2n)是对应点,则点B(a,b)的对应点的坐标为( )
A. B. C. D. 无法确定
二、填空题(本大题共4小题,共20分)
如图,在平面直角坐标系中,OAB的顶点A,B的坐标分别为(3,),(4,0).把OAB沿x轴向右平移得到CDE.若点D的坐标为(6,),则点E的坐标为 .
已知点A的坐标是(1,-1),把平面直角坐标系先向左平移3个单位长度,再向上平移5个单位长度,在新的平面直角坐标系中原来点A的坐标是 .
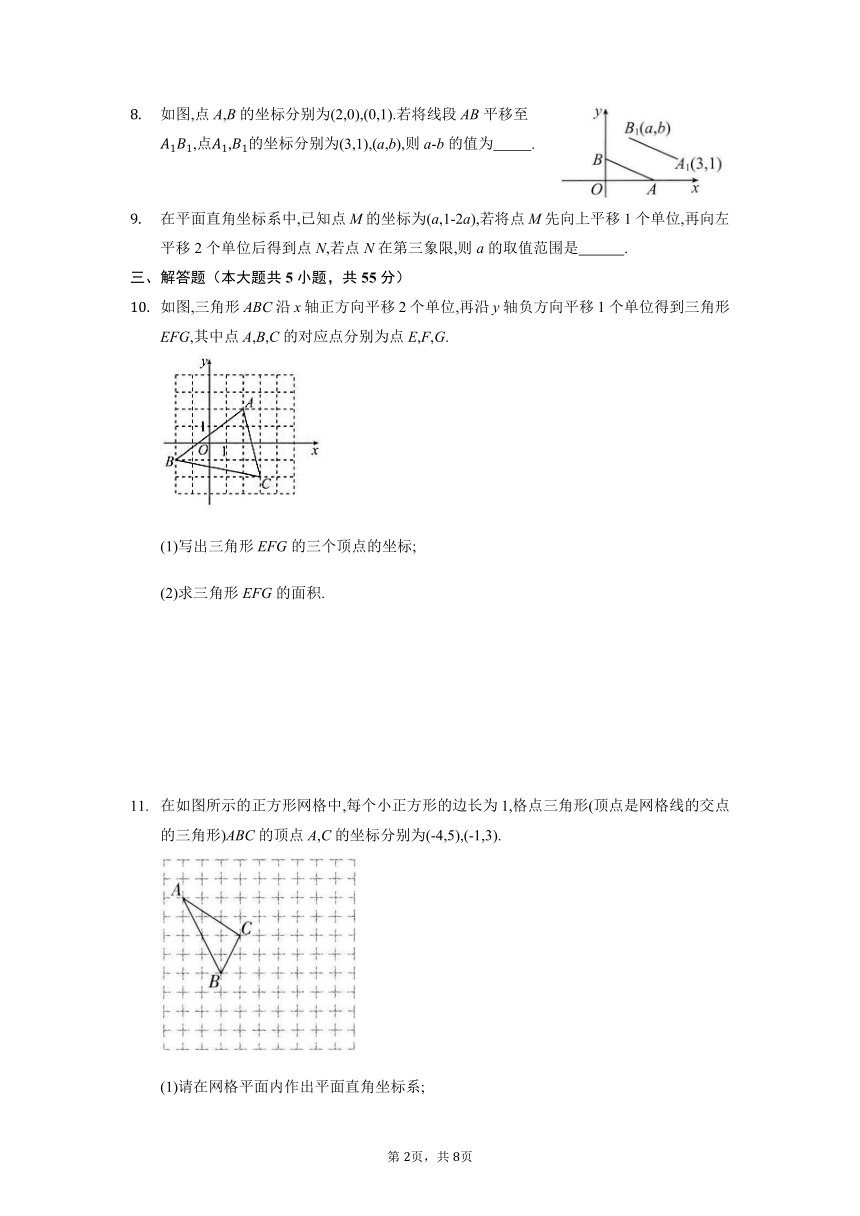
如图,点A,B的坐标分别为(2,0),(0,1).若将线段AB平移至,点,的坐标分别为(3,1),(a,b),则a-b的值为 .
在平面直角坐标系中,已知点M的坐标为(a,1-2a),若将点M先向上平移1个单位,再向左平移2个单位后得到点N,若点N在第三象限,则a的取值范围是 .
三、解答题(本大题共5小题,共55分)
如图,三角形ABC沿x轴正方向平移2个单位,再沿y轴负方向平移1个单位得到三角形EFG,其中点A,B,C的对应点分别为点E,F,G.
(1)写出三角形EFG的三个顶点的坐标;
(2)求三角形EFG的面积.
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在网格平面内作出平面直角坐标系;
(2)将ABC平移至DEF,使得A,B,C的对应点依次是D,E,F,已知D(2,3),请在网格中作出DEF;
(3)若Q(a,b)是DEF内一点,则点Q在ABC内的对应点点P的坐标是 .(用a,b表示)
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.解决问题:
(1)计算{3,1}+{1,2},{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2},平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗 在图①中画出四边形OABC;
(3)如图②,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
如图,一只蚂蚁在网格(每个小正方形的边长均为1)上沿着网格线运动,它从格点A(1,2)处出发去看望格点B,C,D等处的蚂蚁.规定:向上、向右走均为图正,向下、向左走均为负.如:从点A到点B记为AB<+1,+3>,从点B到点A记为BA<-1,-3>,其中第一个数表示左右方向,第二个数表示上下方向.
填空:(1)图中AC< , >,CD< , >;
(2)若这只蚂蚁从点A处去点M处,蚂蚁的行走路线依次为<+3,+3>,<+2,-1>,<-3,-3>,<+4,+2>,则点M的坐标为( , );
(3)若图中另有两个格点P,Q,且PA< m+3,n+2>,PQ< m+1,n-2>,则从点Q到点A记为QA< , >.
如图,是ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为(1,1)、(4,2)、(3,4).
(1)请画出ABC,并写出点A、B、C的坐标;
(2)求与ABC的面积;
(3)求在整个平移过程中,ABC扫过的面积.
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】(7,0)
7.【答案】(4,-6)
8.【答案】-1
9.【答案】1< a< 2
10.【答案】解:(1)点E,F,G的坐标分别为(4,1),(0,-2),(5,-3).
(2)三角形EFG的面积=45-34-15-41=20-6-2.5-2=9.5.
11.【答案】解:(1)建立直角坐标系如图所示.
(2)如图,DEF为所作.
(3)(a-6,b+2).
12.【答案】解:(1){3,1}+{1,2}={4,3},{1,2}+{3,1}={4,3}.
(2)最后的位置仍是B,四边形OABC如图所示.
(3){0,0}+{2,3}+{3,2}+{-5,-5}={0,0}.
13.【答案】解:(1)+3 -1 +1 +3
(2)7 3
(3)+2 +4
14.【答案】解:(1)如图
A(-3,1)、B(0,2)、C(-1,4)
(2)的面积为41=2,ABC的面积为33- 23-12-13=3
(3)由平移的性质,可知四边形C是平行四边形,=.
ABC扫过的面积为+= +=43+3=15
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共5小题,共25分)
在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P'的坐标为( )
A. B. C. D.
ABC的顶点A的坐标为(-2,5),若将ABC沿x轴平移5个单位长度,则A点坐标变为( )
A. B. 或
C. 或 D. 或
如图,在平面直角坐标系中,已知点A(2,1),点B(3,-1),平移线段AB,使点A落在点(-2,2)处,则点B的对应点的坐标为( )
A. B.
C. D.
在平面直角坐标系中,线段CF是由线段AB平移得到的,点A(-2,3)的对应点为C(1,2),则点B(a,b)的对应点F的坐标为( )
A. B. C. D.
将三角形ABC平移得到三角形,若点A(m,n)和点(2m,2n)是对应点,则点B(a,b)的对应点的坐标为( )
A. B. C. D. 无法确定
二、填空题(本大题共4小题,共20分)
如图,在平面直角坐标系中,OAB的顶点A,B的坐标分别为(3,),(4,0).把OAB沿x轴向右平移得到CDE.若点D的坐标为(6,),则点E的坐标为 .
已知点A的坐标是(1,-1),把平面直角坐标系先向左平移3个单位长度,再向上平移5个单位长度,在新的平面直角坐标系中原来点A的坐标是 .
如图,点A,B的坐标分别为(2,0),(0,1).若将线段AB平移至,点,的坐标分别为(3,1),(a,b),则a-b的值为 .
在平面直角坐标系中,已知点M的坐标为(a,1-2a),若将点M先向上平移1个单位,再向左平移2个单位后得到点N,若点N在第三象限,则a的取值范围是 .
三、解答题(本大题共5小题,共55分)
如图,三角形ABC沿x轴正方向平移2个单位,再沿y轴负方向平移1个单位得到三角形EFG,其中点A,B,C的对应点分别为点E,F,G.
(1)写出三角形EFG的三个顶点的坐标;
(2)求三角形EFG的面积.
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在网格平面内作出平面直角坐标系;
(2)将ABC平移至DEF,使得A,B,C的对应点依次是D,E,F,已知D(2,3),请在网格中作出DEF;
(3)若Q(a,b)是DEF内一点,则点Q在ABC内的对应点点P的坐标是 .(用a,b表示)
类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.解决问题:
(1)计算{3,1}+{1,2},{1,2}+{3,1};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2},平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”{3,1}平移,最后的位置还是点B吗 在图①中画出四边形OABC;
(3)如图②,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
如图,一只蚂蚁在网格(每个小正方形的边长均为1)上沿着网格线运动,它从格点A(1,2)处出发去看望格点B,C,D等处的蚂蚁.规定:向上、向右走均为图正,向下、向左走均为负.如:从点A到点B记为AB<+1,+3>,从点B到点A记为BA<-1,-3>,其中第一个数表示左右方向,第二个数表示上下方向.
填空:(1)图中AC< , >,CD< , >;
(2)若这只蚂蚁从点A处去点M处,蚂蚁的行走路线依次为<+3,+3>,<+2,-1>,<-3,-3>,<+4,+2>,则点M的坐标为( , );
(3)若图中另有两个格点P,Q,且PA< m+3,n+2>,PQ< m+1,n-2>,则从点Q到点A记为QA< , >.
如图,是ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为(1,1)、(4,2)、(3,4).
(1)请画出ABC,并写出点A、B、C的坐标;
(2)求与ABC的面积;
(3)求在整个平移过程中,ABC扫过的面积.
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】(7,0)
7.【答案】(4,-6)
8.【答案】-1
9.【答案】1< a< 2
10.【答案】解:(1)点E,F,G的坐标分别为(4,1),(0,-2),(5,-3).
(2)三角形EFG的面积=45-34-15-41=20-6-2.5-2=9.5.
11.【答案】解:(1)建立直角坐标系如图所示.
(2)如图,DEF为所作.
(3)(a-6,b+2).
12.【答案】解:(1){3,1}+{1,2}={4,3},{1,2}+{3,1}={4,3}.
(2)最后的位置仍是B,四边形OABC如图所示.
(3){0,0}+{2,3}+{3,2}+{-5,-5}={0,0}.
13.【答案】解:(1)+3 -1 +1 +3
(2)7 3
(3)+2 +4
14.【答案】解:(1)如图
A(-3,1)、B(0,2)、C(-1,4)
(2)的面积为41=2,ABC的面积为33- 23-12-13=3
(3)由平移的性质,可知四边形C是平行四边形,=.
ABC扫过的面积为+= +=43+3=15
第2页,共2页
