沪科版2021-2022学年八年级数学上册12.2.3 待定系数法 同步测试卷(word版、含答案)
文档属性
| 名称 | 沪科版2021-2022学年八年级数学上册12.2.3 待定系数法 同步测试卷(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 101.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览

文档简介
12.2.3 待定系数法同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共35分)
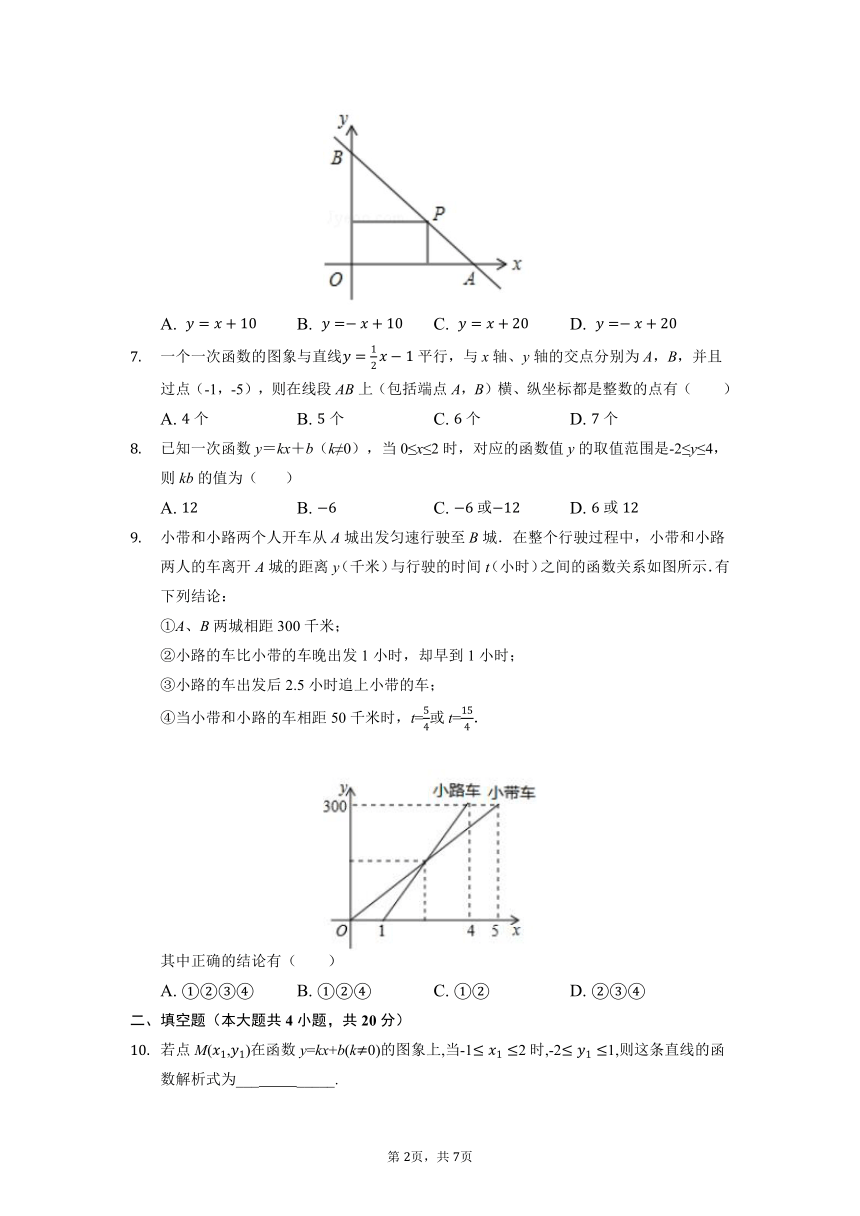
如图,直线AB对应的函数表达式是( )
A. B.
C. D.
已知一次函数y=kx+b(k0),当x=1时,y=3;当x=0时,y=1.则当x=2时,y的值是( )
A. B. C. D.
已知一次函数的图象经过点A(0,3)且与两坐标轴所围成的三角形的面积为3,则这个一次函数的表达式为()
A. B.
C. 或 D. 无法确定
若y-1与2x+3成正比例,且x=2时,y=15,则y关于x的函数解析式为( )
A. B. C. D.
某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A. : B. :
C. : D. :
如图,一直线与两坐标轴的正半轴分别交于,两点,是线段上任意一点(不包括端点),过分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
A. B. C. D.
一个一次函数的图象与直线平行,与x轴、y轴的交点分别为A,B,并且过点(-1,-5),则在线段AB上(包括端点A,B)横、纵坐标都是整数的点有( )
A. 个 B. 个 C. 个 D. 个
已知一次函数y=kx+b(k≠0),当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( )
A. B. C. 或 D. 或
小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人的车离开A城的距离y(千米)与行驶的时间t(小时)之间的函数关系如图所示.有下列结论:
①A、B两城相距300千米;
②小路的车比小带的车晚出发1小时,却早到1小时;
③小路的车出发后2.5小时追上小带的车;
④当小带和小路的车相距50千米时,t=或t=.
其中正确的结论有( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
若点M(,)在函数y=kx+b(k0)的图象上,当-12时,-21,则这条直线的函数解析式为___ _____.
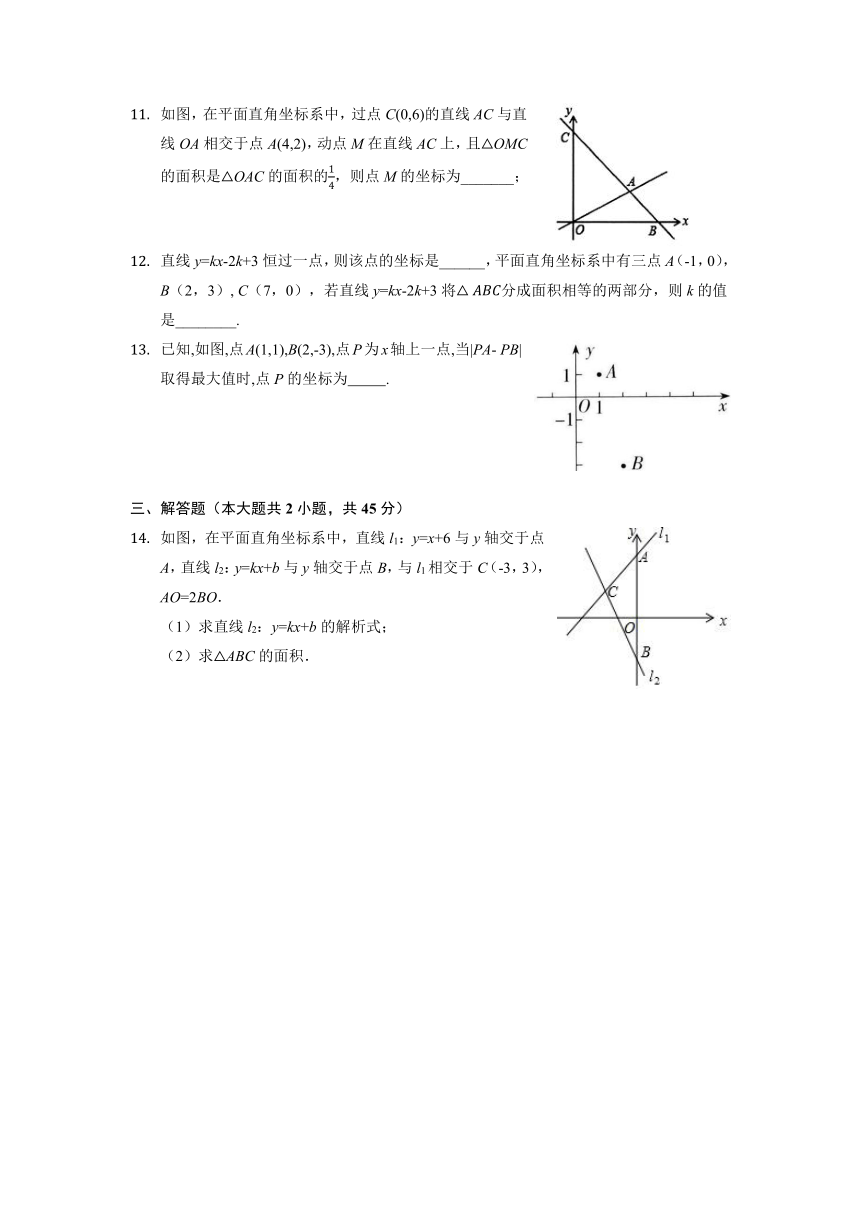
如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在直线AC上,且OMC的面积是OAC的面积的,则点M的坐标为_______;
直线y=kx-2k+3恒过一点,则该点的坐标是______,平面直角坐标系中有三点A(-1,0),B(2,3), C(7,0),若直线y=kx-2k+3将分成面积相等的两部分,则k的值是________.
已知,如图,点A(1,1),B(2,-3),点P为x轴上一点,当|PA- PB|取得最大值时,点P的坐标为 .
三、解答题(本大题共2小题,共45分)
如图,在平面直角坐标系中,直线l1:y=x+6与y轴交于点A,直线l2:y=kx+b与y轴交于点B,与l1相交于C(-3,3),AO=2BO.
(1)求直线l2:y=kx+b的解析式;
(2)求△ABC的面积.
如图所示,直线的解析式为y=-3x+3,且与x轴交于点D,直线经过点A,B,直线,交于点C.
(1)求点D的坐标;
(2)求直线的解析式;
(3)求ADC的面积;
(4)在直线上存在异于点C的另一点P,使得ADP与ADC的面积相等,请直接写出点P的坐标.
(5)在x轴上求作一点M,使得BM+CM的和最小,直接写出点M的坐标.
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】y=x-1或y=-x
11.【答案】(1,5)或(-1,7)
12.【答案】(2,3),-3
13.【答案】(, 0)
14.【答案】解:(1)∵直线l1:y=x+6与y轴交于点A,
∴当x=0时,y=0+6=6,
∴A(0,6),
∵AO=2BO,
∴B(0,-3),
∵C(-3,3),
代入直线l2:y=kx+b中得,
解得.
故直线l2的解析式为y=-2x-3;
(2)S△ABC=AB |xC|=×(6+3)×3=.
15.【答案】解:(1)由y=-3x+3,令y=0,得-3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b(k≠0),
∵A(4,0),,
∴
∴,
∴直线l2的解析表达式为;
(3)由,
解得,
∴C(2,-3),
∵AD=3,
∴;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是C到AD的距离,
即C纵坐标的绝对值=|-3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
把y=3代入l2得1.5x-6=3
∴x=6,
∴P(6,3).
(5)作B点关于x轴的对称点B',连CB'与x轴的交点即是M点,
∴B'(3,),
设CB'的解析式为y=mx+n,
∴,
∴,
∴CB'的解析式为y=,
令y=0,得x=,
∴M().
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共35分)
如图,直线AB对应的函数表达式是( )
A. B.
C. D.
已知一次函数y=kx+b(k0),当x=1时,y=3;当x=0时,y=1.则当x=2时,y的值是( )
A. B. C. D.
已知一次函数的图象经过点A(0,3)且与两坐标轴所围成的三角形的面积为3,则这个一次函数的表达式为()
A. B.
C. 或 D. 无法确定
若y-1与2x+3成正比例,且x=2时,y=15,则y关于x的函数解析式为( )
A. B. C. D.
某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A. : B. :
C. : D. :
如图,一直线与两坐标轴的正半轴分别交于,两点,是线段上任意一点(不包括端点),过分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
A. B. C. D.
一个一次函数的图象与直线平行,与x轴、y轴的交点分别为A,B,并且过点(-1,-5),则在线段AB上(包括端点A,B)横、纵坐标都是整数的点有( )
A. 个 B. 个 C. 个 D. 个
已知一次函数y=kx+b(k≠0),当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( )
A. B. C. 或 D. 或
小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人的车离开A城的距离y(千米)与行驶的时间t(小时)之间的函数关系如图所示.有下列结论:
①A、B两城相距300千米;
②小路的车比小带的车晚出发1小时,却早到1小时;
③小路的车出发后2.5小时追上小带的车;
④当小带和小路的车相距50千米时,t=或t=.
其中正确的结论有( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
若点M(,)在函数y=kx+b(k0)的图象上,当-12时,-21,则这条直线的函数解析式为___ _____.
如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2),动点M在直线AC上,且OMC的面积是OAC的面积的,则点M的坐标为_______;
直线y=kx-2k+3恒过一点,则该点的坐标是______,平面直角坐标系中有三点A(-1,0),B(2,3), C(7,0),若直线y=kx-2k+3将分成面积相等的两部分,则k的值是________.
已知,如图,点A(1,1),B(2,-3),点P为x轴上一点,当|PA- PB|取得最大值时,点P的坐标为 .
三、解答题(本大题共2小题,共45分)
如图,在平面直角坐标系中,直线l1:y=x+6与y轴交于点A,直线l2:y=kx+b与y轴交于点B,与l1相交于C(-3,3),AO=2BO.
(1)求直线l2:y=kx+b的解析式;
(2)求△ABC的面积.
如图所示,直线的解析式为y=-3x+3,且与x轴交于点D,直线经过点A,B,直线,交于点C.
(1)求点D的坐标;
(2)求直线的解析式;
(3)求ADC的面积;
(4)在直线上存在异于点C的另一点P,使得ADP与ADC的面积相等,请直接写出点P的坐标.
(5)在x轴上求作一点M,使得BM+CM的和最小,直接写出点M的坐标.
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】y=x-1或y=-x
11.【答案】(1,5)或(-1,7)
12.【答案】(2,3),-3
13.【答案】(, 0)
14.【答案】解:(1)∵直线l1:y=x+6与y轴交于点A,
∴当x=0时,y=0+6=6,
∴A(0,6),
∵AO=2BO,
∴B(0,-3),
∵C(-3,3),
代入直线l2:y=kx+b中得,
解得.
故直线l2的解析式为y=-2x-3;
(2)S△ABC=AB |xC|=×(6+3)×3=.
15.【答案】解:(1)由y=-3x+3,令y=0,得-3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b(k≠0),
∵A(4,0),,
∴
∴,
∴直线l2的解析表达式为;
(3)由,
解得,
∴C(2,-3),
∵AD=3,
∴;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是C到AD的距离,
即C纵坐标的绝对值=|-3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
把y=3代入l2得1.5x-6=3
∴x=6,
∴P(6,3).
(5)作B点关于x轴的对称点B',连CB'与x轴的交点即是M点,
∴B'(3,),
设CB'的解析式为y=mx+n,
∴,
∴,
∴CB'的解析式为y=,
令y=0,得x=,
∴M().
第2页,共2页
