沪科版八年级数学上册2021-2022学年12.2.4 一次函数的应用 同步测试卷(word版、含答案)
文档属性
| 名称 | 沪科版八年级数学上册2021-2022学年12.2.4 一次函数的应用 同步测试卷(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 177.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 07:00:30 | ||
图片预览



文档简介
12.2.4 一次函数的应用同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共35分)
如图是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象,那么从图象中可看出,复印超过100面的部分,每面收费( )
A. 元 B. 元 C. 元 D. 元
如图,反映了某公司的销售收入与销售量的关系,反映了该公司的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( )
A. 小于 B. 大于
C. 小于 D. 大于
一个有进水管与出水管的容器,从某时刻开始的4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.根据图象提供的信息,下列结论中错误的是( )
A. 第时,容器内的水量为 B. 每分钟的进水量为
C. 每分钟的出水量为 D. 第时,容器内的水量为
两地相距60 km,甲从地去地,乙从地去地,图中、分别表示甲、乙两人到地的距离与甲出发时间的函数关系图象.两人之间恰好相距时,甲出发了( )时.
A. B. 或 C. D. 或
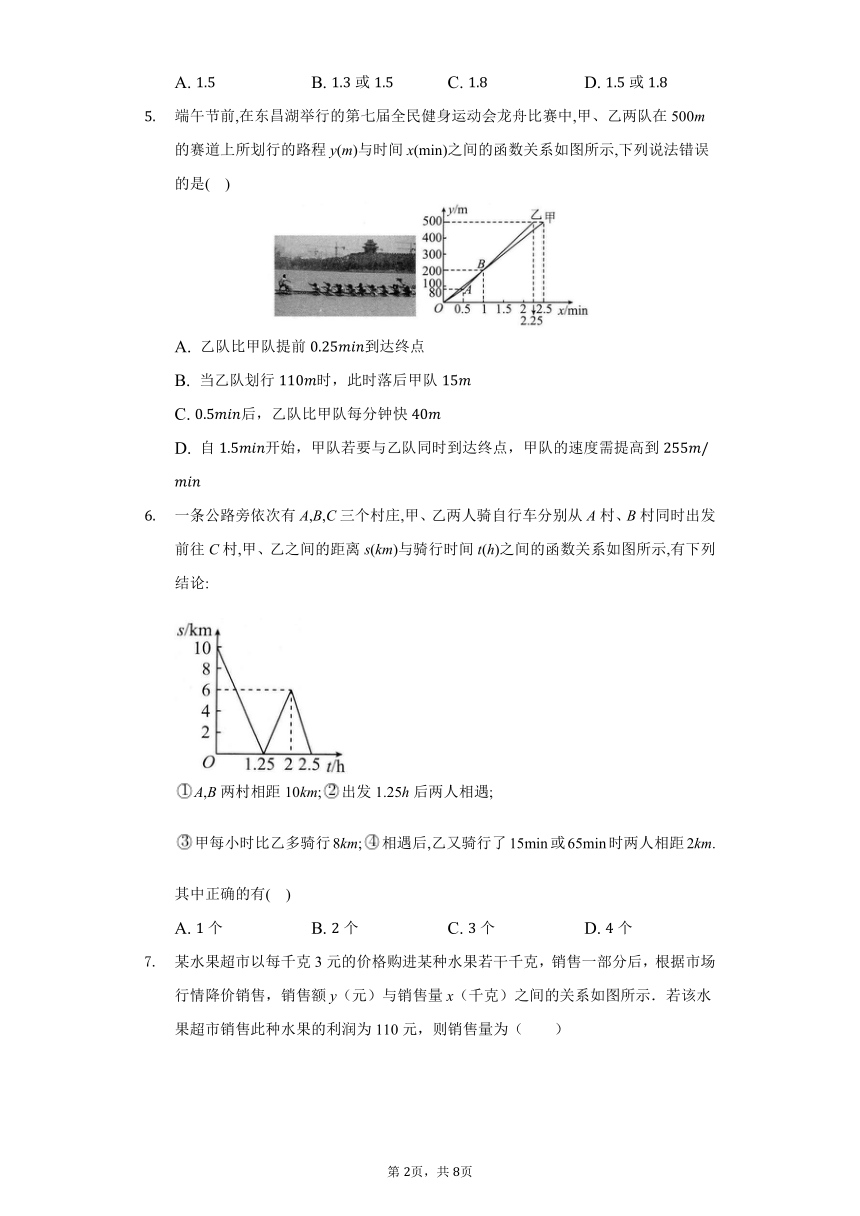
端午节前,在东昌湖举行的第七届全民健身运动会龙舟比赛中,甲、乙两队在500m的赛道上所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法错误的是( )
A. 乙队比甲队提前到达终点
B. 当乙队划行时,此时落后甲队
C. 后,乙队比甲队每分钟快
D. 自开始,甲队若要与乙队同时到达终点,甲队的速度需提高到
一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,有下列结论:
A,B两村相距10km;出发1.25h后两人相遇;
甲每小时比乙多骑行8km;相遇后,乙又骑行了15min或65min时两人相距2km.
其中正确的有( )
A. 个 B. 个 C. 个 D. 个
某水果超市以每千克3元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额 y(元)与销售量x(千克)之间的关系如图所示.若该水果超市销售此种水果的利润为110元,则销售量为( )
A. 千克 B. 千克 C. 千克 D. 千克
如图,点,,在一次函数的图象上,它们的横坐标依次为,,,分别过这些点作轴与轴的垂线,则图中阴影部分的面积之和是( )
A. B.
C. D.
A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论:①甲骑车速度为30km/小时,乙的速度为20km/小时;②l1的函数表达式为y=80-30x;③l2的函数表达式为y=20x;④小时后两人相遇,其中正确的个数是( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共4小题,共20分)
摄氏度(℃)与华氏度(℉)都是用来表示物体温度的.用x与y分别表示华氏度(℉) 与摄氏度(℃),y是x的一次函数,其表达式为y=x-.在疫情期间,使用额温枪测某同学体温显示为96.8 ℉,调回摄氏度模式下测量,其温度大约是 ℃.
如图,折线ABC是某市区出租车所收费用y(元)与出租车行驶路程x(km)之间的函数关系图象,某人支付车费15.6元,则出租车走了 km.
甲、乙两人分别从A,B两地出发相向而行,他们距B地的距离s(km)与时间t(h)的关系如图所示,那么乙的速度是 km/h.
若A(,),B(,)是一次函数y=ax+x-2图象上的不同的两点,记m=(-)(-),则当m<0时,a的取值范围是 .
三、解答题(本大题共2小题,共45分)
某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲 乙
购树苗数量 销售价格 购树苗数量 销售价格
不超过500棵时 800元/棵 不超过1000棵时 800元/棵
超过500棵的部分 700元/棵 超过1000棵的部分 600元/棵
设购买银杏树苗x棵,到两家购买所需费用分别为元、元.
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买,所需费用为 元;若都在乙家购买,所需费用为 元;
(2)当x>1000时,分别求出,与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么
如图,A,B两地相距60km,甲从A地去B地,乙从B地去A地,图中,分别表示甲、乙两人离B地的距离y(km)与甲出发的时间x(h)之间的函数关系图象.
(1)根据图象,直接写出乙的行驶速度是 ;
(2)解释交点A的实际意义;
(3)甲出发多长时间,两人之间的距离恰好相距5km;
(4)若用(km)表示甲、乙两人之间的距离,请建立平面直角坐标系画出(km)关于时间x(h)的函数关系图象,并注明关键点的数据.
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】36
11.【答案】10
12.【答案】3.6
13.【答案】a<-1
14.【答案】解:(1)610000 640000
(2)当x>1000时,=800500+700(x-500)=700x+50000(x为正整数);
=8001000+600(x-1000)=600x+200000(x为正整数).
(3)当0x500时,到两家购买所需费用一样;
当500< x1000时,甲家有优惠而乙家无优惠,所以到甲家购买合算;
当x>1000时,又-=100x-150000.
当=时,100x-150000=0,解得x=1500,
所以当x=1500时,到两家购买所需费用一样;
当<时,100x-150000<0,解得x<1500,
所以当1000< x<1500时,到甲家购买合算;
当>时,100x-150000>0,解得x>1500,
所以当x>1500时,到乙家购买合算.
综上所述,当0x500或x=1500时,到两家购买所需费用一样;
当500< x<1500时,到甲家购买合算;
当x>1500时,到乙家购买合算.
15.【答案】解:(1)20km/h;
(2)设直线的函数表达式为=x+.
由题意,得解得
即直线的函数表达式为=-30x+60.
设直线的函数表达式为=x+.
由题意,得解得
即直线的函数表达式为=20x-10.
联立解得
即点A的坐标为(1.4,18),
所以点A的实际意义是在甲出发1.4h时,甲、乙两人相遇,此时距离B地18km.
(3)由题意可得,|(-30x+60)-(20x-10)|=5,
解得=1.3,=1.5.
答:当甲出发1.3h或1.5h时,两人之间的距离恰好相距5km.
(4)由题意可得,
当0x0.5时,=-30x+60;
当0.5<x1.4时,=-=(-30x+60)-(20x-10)=-50x+70;
当1.4<x2时,=-=(20x-10)-(-30x+60)=50x-70;
当2<x3.5时,=20x-10.
所以(km)关于时间x(h)的函数关系图象如图所示.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共35分)
如图是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象,那么从图象中可看出,复印超过100面的部分,每面收费( )
A. 元 B. 元 C. 元 D. 元
如图,反映了某公司的销售收入与销售量的关系,反映了该公司的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量( )
A. 小于 B. 大于
C. 小于 D. 大于
一个有进水管与出水管的容器,从某时刻开始的4 min内只进水不出水,在随后的8 min内既进水又出水,每分钟的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.根据图象提供的信息,下列结论中错误的是( )
A. 第时,容器内的水量为 B. 每分钟的进水量为
C. 每分钟的出水量为 D. 第时,容器内的水量为
两地相距60 km,甲从地去地,乙从地去地,图中、分别表示甲、乙两人到地的距离与甲出发时间的函数关系图象.两人之间恰好相距时,甲出发了( )时.
A. B. 或 C. D. 或
端午节前,在东昌湖举行的第七届全民健身运动会龙舟比赛中,甲、乙两队在500m的赛道上所划行的路程y(m)与时间x(min)之间的函数关系如图所示,下列说法错误的是( )
A. 乙队比甲队提前到达终点
B. 当乙队划行时,此时落后甲队
C. 后,乙队比甲队每分钟快
D. 自开始,甲队若要与乙队同时到达终点,甲队的速度需提高到
一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,有下列结论:
A,B两村相距10km;出发1.25h后两人相遇;
甲每小时比乙多骑行8km;相遇后,乙又骑行了15min或65min时两人相距2km.
其中正确的有( )
A. 个 B. 个 C. 个 D. 个
某水果超市以每千克3元的价格购进某种水果若干千克,销售一部分后,根据市场行情降价销售,销售额 y(元)与销售量x(千克)之间的关系如图所示.若该水果超市销售此种水果的利润为110元,则销售量为( )
A. 千克 B. 千克 C. 千克 D. 千克
如图,点,,在一次函数的图象上,它们的横坐标依次为,,,分别过这些点作轴与轴的垂线,则图中阴影部分的面积之和是( )
A. B.
C. D.
A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论:①甲骑车速度为30km/小时,乙的速度为20km/小时;②l1的函数表达式为y=80-30x;③l2的函数表达式为y=20x;④小时后两人相遇,其中正确的个数是( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共4小题,共20分)
摄氏度(℃)与华氏度(℉)都是用来表示物体温度的.用x与y分别表示华氏度(℉) 与摄氏度(℃),y是x的一次函数,其表达式为y=x-.在疫情期间,使用额温枪测某同学体温显示为96.8 ℉,调回摄氏度模式下测量,其温度大约是 ℃.
如图,折线ABC是某市区出租车所收费用y(元)与出租车行驶路程x(km)之间的函数关系图象,某人支付车费15.6元,则出租车走了 km.
甲、乙两人分别从A,B两地出发相向而行,他们距B地的距离s(km)与时间t(h)的关系如图所示,那么乙的速度是 km/h.
若A(,),B(,)是一次函数y=ax+x-2图象上的不同的两点,记m=(-)(-),则当m<0时,a的取值范围是 .
三、解答题(本大题共2小题,共45分)
某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲 乙
购树苗数量 销售价格 购树苗数量 销售价格
不超过500棵时 800元/棵 不超过1000棵时 800元/棵
超过500棵的部分 700元/棵 超过1000棵的部分 600元/棵
设购买银杏树苗x棵,到两家购买所需费用分别为元、元.
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买,所需费用为 元;若都在乙家购买,所需费用为 元;
(2)当x>1000时,分别求出,与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么
如图,A,B两地相距60km,甲从A地去B地,乙从B地去A地,图中,分别表示甲、乙两人离B地的距离y(km)与甲出发的时间x(h)之间的函数关系图象.
(1)根据图象,直接写出乙的行驶速度是 ;
(2)解释交点A的实际意义;
(3)甲出发多长时间,两人之间的距离恰好相距5km;
(4)若用(km)表示甲、乙两人之间的距离,请建立平面直角坐标系画出(km)关于时间x(h)的函数关系图象,并注明关键点的数据.
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】36
11.【答案】10
12.【答案】3.6
13.【答案】a<-1
14.【答案】解:(1)610000 640000
(2)当x>1000时,=800500+700(x-500)=700x+50000(x为正整数);
=8001000+600(x-1000)=600x+200000(x为正整数).
(3)当0x500时,到两家购买所需费用一样;
当500< x1000时,甲家有优惠而乙家无优惠,所以到甲家购买合算;
当x>1000时,又-=100x-150000.
当=时,100x-150000=0,解得x=1500,
所以当x=1500时,到两家购买所需费用一样;
当<时,100x-150000<0,解得x<1500,
所以当1000< x<1500时,到甲家购买合算;
当>时,100x-150000>0,解得x>1500,
所以当x>1500时,到乙家购买合算.
综上所述,当0x500或x=1500时,到两家购买所需费用一样;
当500< x<1500时,到甲家购买合算;
当x>1500时,到乙家购买合算.
15.【答案】解:(1)20km/h;
(2)设直线的函数表达式为=x+.
由题意,得解得
即直线的函数表达式为=-30x+60.
设直线的函数表达式为=x+.
由题意,得解得
即直线的函数表达式为=20x-10.
联立解得
即点A的坐标为(1.4,18),
所以点A的实际意义是在甲出发1.4h时,甲、乙两人相遇,此时距离B地18km.
(3)由题意可得,|(-30x+60)-(20x-10)|=5,
解得=1.3,=1.5.
答:当甲出发1.3h或1.5h时,两人之间的距离恰好相距5km.
(4)由题意可得,
当0x0.5时,=-30x+60;
当0.5<x1.4时,=-=(-30x+60)-(20x-10)=-50x+70;
当1.4<x2时,=-=(20x-10)-(-30x+60)=50x-70;
当2<x3.5时,=20x-10.
所以(km)关于时间x(h)的函数关系图象如图所示.
第2页,共3页
