2021-2022学年鲁教版(五四制)九年级数学下册5.10圆锥的侧面积 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.10圆锥的侧面积 同步达标测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 08:44:07 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学下册《5.10圆锥的侧面积》同步达标测评(附答案)
一.选择题(共12小题,满分48分)
1.圆锥的底面半径为10cm,母线长为15cm,则这个圆锥的侧面积是( )
A.100πcm2 B.150πcm2 C.200πcm2 D.250πcm2
2.将弧长为2πcm、圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高是( )
A. cm B.2 cm C.2 cm D. cm
3.已知圆锥的侧面积是3π,母线是3,则圆锥的高为( )
A.2 B.2 C. D.
4.如图,在Rt△ABC中,∠B=90°,AC=5,BC=4,以AC所在的直线为轴旋转一周所成几何体的表面积为( )
A. B. C. D.12π
5.如图,AO是圆锥的高,圆锥的底面半径OB=0.7,AB的长为2.5,则AO的长为( )
A.2.4 B.2.2 C.1.8 D.1.6
6.用半径为8的半圆围成一个圆锥的侧面,则圆锥的底面半径等于( )
A.4 B.6 C.16π D.8
7.圆锥的底面半径为1,侧面积为3π,则其侧面展开图的圆心角为( )
A.90° B.120° C.150° D.180°
8.将一个半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的面积是( )cm2
A.60π B.90π C.120π D.I50π
9.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )A.3 B.2 C.1.5 D.1
11.已知圆柱的底面半径为2cm,高为4cm,则圆柱的侧面积是( )
A.16cm2 B.16πcm2 C.8πcm2 D.4πcm2
12.圆柱的底面直径为8,母线长为5,则它的侧面积是( )
A.20 B.20π C.40 D.40π
二.填空题(共7小题,满分35分)
13.某圆锥的底面圆的半径为5,高为12,则圆锥的表面积为 .(结果保留π)
14.一个水平放置的圆锥的主视图为底边长2cm、腰长3cm的等腰三角形,则该圆锥的表面积是 .
15.如图,已知圆锥的母线SA的长为4,底面半径OA的长为2,则圆锥的侧面积等于 .
16.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是 cm2.
17.一个圆柱的高缩小2 倍,底面半径扩大2 倍,表面积不变. .(判断对错)
18.已知圆柱的侧面积是20πcm2,高为5cm,则圆柱的底面半径为 .
19.底面直径和高都是1的圆柱侧面积为 .
三.解答题(共4小题,满分37分)
20.如图,圆锥的底面半径为6cm,高为8cm,求这个圆锥的侧面积和表面积.
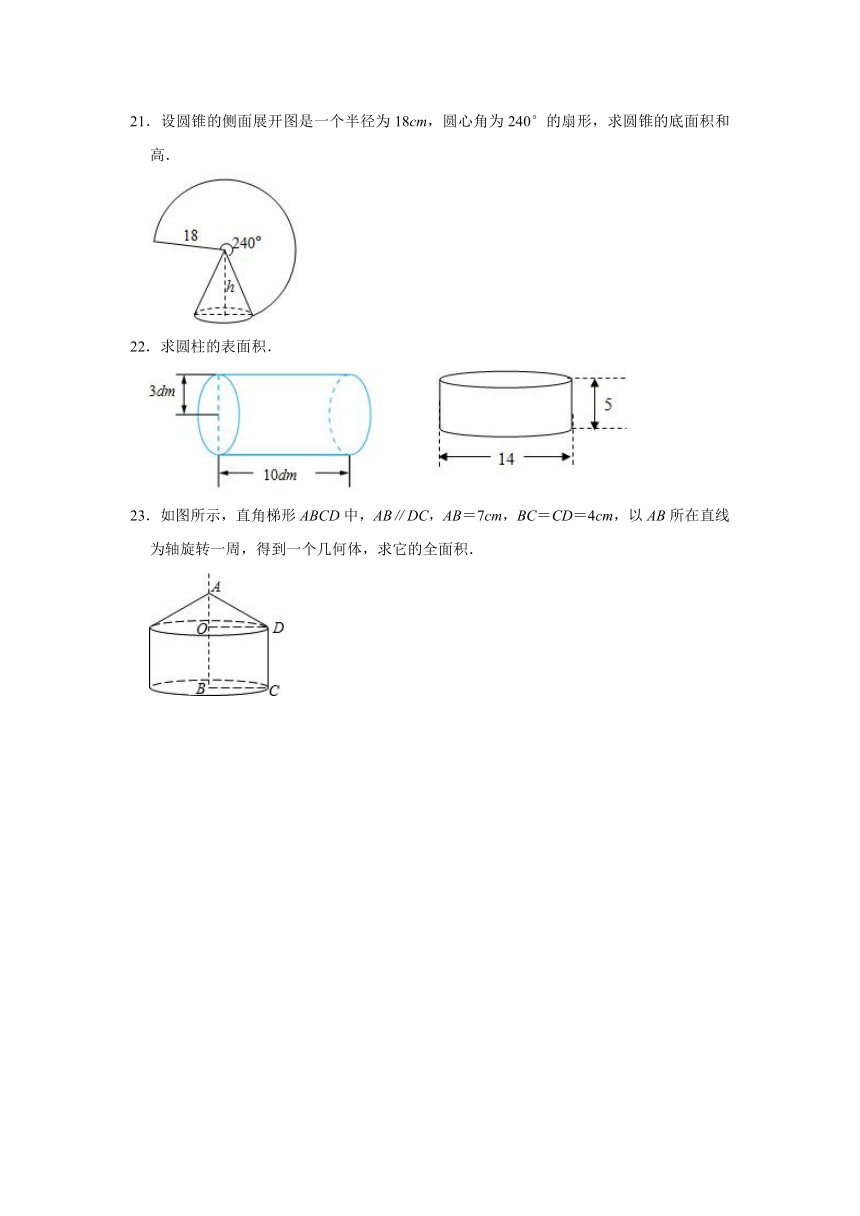
21.设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
22.求圆柱的表面积.
23.如图所示,直角梯形ABCD中,AB∥DC,AB=7cm,BC=CD=4cm,以AB所在直线为轴旋转一周,得到一个几何体,求它的全面积.
参考答案
一.选择题(共12小题,满分48分)
1.解:圆锥的底面周长是:2×10π=20π,
则×20π×15=150π.
故选:B.
2.解:设圆锥的底面圆的半径为r,
则2πr=2π,解得r=1;
设圆锥的母线长为l,
则=2π,解得l=3,
所以圆锥的高==2(cm).
故选:B.
3.解:设圆锥的底面圆的半径为r,
根据题意得 2πr 3=3π,解得r=1,
所以圆锥的高==2.
故选:B.
4.解:作BH⊥AC于H,如图,
AB==3,
∵BH AC=AB BC,
∴BH==,
∴以AC所在的直线为轴旋转一周所成几何体的表面积= 2π 4+ 2π 3=π.
故选:A.
5.解:由勾股定理得,AO==2.4,
故选:A.
6.解:由题意知:底面周长=8π,
∴底面半径=8π÷2π=4.
故选:A.
7.解:设圆锥的母线长为l,
则×2π×1×l=3π,解得l=3,
设圆锥的侧面展开图的圆心角为n°,
则=3π,解得n=120,
即圆锥的侧面展开图的圆心角为120°.
故选:B.
8.解:所得圆锥的侧面展开图的面积=×2π×6×15=90π(cm2).
故选:B.
9.解:设此圆锥的底面半径为rcm,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
2πr=,
解得:r=1.
故选:D.
11.解:根据侧面积公式可得π×2×2×4=16πcm2.
故圆柱的侧面积是16πcm2.
故选:B.
12.解:∵圆柱的底面直径为8,母线长为5,
∴它的侧面积是8π×5=40π.
故选:D.
二.填空题(共7小题,满分35分)
13.解:∵圆锥的底面半径为5,高为12,
∴圆锥的侧面积为13,
∴它的侧面积=π×13×5=65π,
它的底面积=π×5×5=25π,
圆锥的表面积=90π,
故答案为:90π
14.解:该圆锥的表面积=×2π×1×3+π 12=4π(cm2).
故答案为4πcm2.
15.解:侧面积=4×4π÷2=8π.
故答案为8π.
16.解:π×2×3×5=30πcm2,
故答案为30π.
17.解:设原圆柱的高为h,底面半径为r,
现在的圆柱的高为h,底面半径为2r,
∴原表面积=2πr2 h,
现在的表面积=2π (2r)2h=4πr2h,
∴表面积发生了变化,
故答案为:错误.
18.解:设圆柱底面圆的半径为r,那么侧面积为
2πr×5=20π
r=2cm.
故答案为2cm.
19.解:圆柱的底面周长=π×1=π.
圆柱的侧面积=底面周长×高=π×1=π.
故答案是:π.
三.解答题(共4小题,满分37分)
20.解:∵圆锥的底面半径为6cm,高为8cm,
∴圆锥的母线长为10cm,
∴S侧=π×6×10=60πcm2;
∵圆锥的底面积=π×62=36π,
∴S表=60π+36π=96πcm2.
21.解:圆锥的弧长为:=24π,
∴圆锥的底面半径为24π÷2π=12,
∴圆锥的底面积为π×122=144π,
∴圆锥的高为=6.
22.解:圆柱的表面积=2πr2+πdh=2π×32+π×6×10=78π;
圆柱的表面积=2πr2+πdh=2π×72+π×14×5=168π.
23.解:∵Rt△AOD中,AO=7﹣4=3cm,OD=4cm,
∴AD==5cm,
∴所得到的几何体的表面积为π×4×5+π×4×2×4+π×4×4=68πcm2.
故它的全面积为68πcm2.
一.选择题(共12小题,满分48分)
1.圆锥的底面半径为10cm,母线长为15cm,则这个圆锥的侧面积是( )
A.100πcm2 B.150πcm2 C.200πcm2 D.250πcm2
2.将弧长为2πcm、圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高是( )
A. cm B.2 cm C.2 cm D. cm
3.已知圆锥的侧面积是3π,母线是3,则圆锥的高为( )
A.2 B.2 C. D.
4.如图,在Rt△ABC中,∠B=90°,AC=5,BC=4,以AC所在的直线为轴旋转一周所成几何体的表面积为( )
A. B. C. D.12π
5.如图,AO是圆锥的高,圆锥的底面半径OB=0.7,AB的长为2.5,则AO的长为( )
A.2.4 B.2.2 C.1.8 D.1.6
6.用半径为8的半圆围成一个圆锥的侧面,则圆锥的底面半径等于( )
A.4 B.6 C.16π D.8
7.圆锥的底面半径为1,侧面积为3π,则其侧面展开图的圆心角为( )
A.90° B.120° C.150° D.180°
8.将一个半径为6cm,母线长为15cm的圆锥形纸筒沿一条母线剪开并展平,所得的侧面展开图的面积是( )cm2
A.60π B.90π C.120π D.I50π
9.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )A.3 B.2 C.1.5 D.1
11.已知圆柱的底面半径为2cm,高为4cm,则圆柱的侧面积是( )
A.16cm2 B.16πcm2 C.8πcm2 D.4πcm2
12.圆柱的底面直径为8,母线长为5,则它的侧面积是( )
A.20 B.20π C.40 D.40π
二.填空题(共7小题,满分35分)
13.某圆锥的底面圆的半径为5,高为12,则圆锥的表面积为 .(结果保留π)
14.一个水平放置的圆锥的主视图为底边长2cm、腰长3cm的等腰三角形,则该圆锥的表面积是 .
15.如图,已知圆锥的母线SA的长为4,底面半径OA的长为2,则圆锥的侧面积等于 .
16.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是 cm2.
17.一个圆柱的高缩小2 倍,底面半径扩大2 倍,表面积不变. .(判断对错)
18.已知圆柱的侧面积是20πcm2,高为5cm,则圆柱的底面半径为 .
19.底面直径和高都是1的圆柱侧面积为 .
三.解答题(共4小题,满分37分)
20.如图,圆锥的底面半径为6cm,高为8cm,求这个圆锥的侧面积和表面积.
21.设圆锥的侧面展开图是一个半径为18cm,圆心角为240°的扇形,求圆锥的底面积和高.
22.求圆柱的表面积.
23.如图所示,直角梯形ABCD中,AB∥DC,AB=7cm,BC=CD=4cm,以AB所在直线为轴旋转一周,得到一个几何体,求它的全面积.
参考答案
一.选择题(共12小题,满分48分)
1.解:圆锥的底面周长是:2×10π=20π,
则×20π×15=150π.
故选:B.
2.解:设圆锥的底面圆的半径为r,
则2πr=2π,解得r=1;
设圆锥的母线长为l,
则=2π,解得l=3,
所以圆锥的高==2(cm).
故选:B.
3.解:设圆锥的底面圆的半径为r,
根据题意得 2πr 3=3π,解得r=1,
所以圆锥的高==2.
故选:B.
4.解:作BH⊥AC于H,如图,
AB==3,
∵BH AC=AB BC,
∴BH==,
∴以AC所在的直线为轴旋转一周所成几何体的表面积= 2π 4+ 2π 3=π.
故选:A.
5.解:由勾股定理得,AO==2.4,
故选:A.
6.解:由题意知:底面周长=8π,
∴底面半径=8π÷2π=4.
故选:A.
7.解:设圆锥的母线长为l,
则×2π×1×l=3π,解得l=3,
设圆锥的侧面展开图的圆心角为n°,
则=3π,解得n=120,
即圆锥的侧面展开图的圆心角为120°.
故选:B.
8.解:所得圆锥的侧面展开图的面积=×2π×6×15=90π(cm2).
故选:B.
9.解:设此圆锥的底面半径为rcm,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
2πr=,
解得:r=1.
故选:D.
11.解:根据侧面积公式可得π×2×2×4=16πcm2.
故圆柱的侧面积是16πcm2.
故选:B.
12.解:∵圆柱的底面直径为8,母线长为5,
∴它的侧面积是8π×5=40π.
故选:D.
二.填空题(共7小题,满分35分)
13.解:∵圆锥的底面半径为5,高为12,
∴圆锥的侧面积为13,
∴它的侧面积=π×13×5=65π,
它的底面积=π×5×5=25π,
圆锥的表面积=90π,
故答案为:90π
14.解:该圆锥的表面积=×2π×1×3+π 12=4π(cm2).
故答案为4πcm2.
15.解:侧面积=4×4π÷2=8π.
故答案为8π.
16.解:π×2×3×5=30πcm2,
故答案为30π.
17.解:设原圆柱的高为h,底面半径为r,
现在的圆柱的高为h,底面半径为2r,
∴原表面积=2πr2 h,
现在的表面积=2π (2r)2h=4πr2h,
∴表面积发生了变化,
故答案为:错误.
18.解:设圆柱底面圆的半径为r,那么侧面积为
2πr×5=20π
r=2cm.
故答案为2cm.
19.解:圆柱的底面周长=π×1=π.
圆柱的侧面积=底面周长×高=π×1=π.
故答案是:π.
三.解答题(共4小题,满分37分)
20.解:∵圆锥的底面半径为6cm,高为8cm,
∴圆锥的母线长为10cm,
∴S侧=π×6×10=60πcm2;
∵圆锥的底面积=π×62=36π,
∴S表=60π+36π=96πcm2.
21.解:圆锥的弧长为:=24π,
∴圆锥的底面半径为24π÷2π=12,
∴圆锥的底面积为π×122=144π,
∴圆锥的高为=6.
22.解:圆柱的表面积=2πr2+πdh=2π×32+π×6×10=78π;
圆柱的表面积=2πr2+πdh=2π×72+π×14×5=168π.
23.解:∵Rt△AOD中,AO=7﹣4=3cm,OD=4cm,
∴AD==5cm,
∴所得到的几何体的表面积为π×4×5+π×4×2×4+π×4×4=68πcm2.
故它的全面积为68πcm2.
