2021-2022学年沪科版八年级数学上册13.1 三角形中的边角关系 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版八年级数学上册13.1 三角形中的边角关系 同步测试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 135.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览



文档简介
13.1 三角形中的边角关系同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共18小题,共54分)
三角形按边分类可分为( )
A. 不等边三角形、等边三角形
B. 等腰三角形、等边三角形
C. 不等边三角形、等腰三角形、等边三角形
D. 不等边三角形、等腰三角形
在课堂上,老师在黑板上画出了如图所示的三个三角形,让同学们根据它们的边长进行分类,其中说法错误的是( )
A. 是不等边三角形 B. 是等腰三角形
C. 是等边三角形 D. 是等边三角形
设三角形三边之长分别为3,8,1-2a,则a的取值范围为( )
A. B.
C. D. 或
长度分别为8,6,6,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A. B. C. D.
已知a,b,c是ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )
A. B. C. D.
已知等腰三角形一边长为4,另一边长为8,则这个等腰三角形的周长为( )
A. B. 或 C. D.
长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A. B. C. D.
已知ABC是锐角三角形,A=,则B的度数可以是( )
A. B. C. D.
在ABC中,A比B大,则ABC的形状是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 无法判断
在ABC中,如果A+B+2C=,那么ABC是( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 锐角三角形或钝角三角形
如图,在ABC中,B=,MNAC,1=,则C的度数是( )
A. B.
C. D.
如图,在RtABC中,ACB=,点D在AB边上,将CBD沿CD折叠,使点B恰好落在AC边上的点E处.若A=,则CDE的度数是( )
A. B. C. D.
如图,在ABC中,EFD=,且AEF=AFE,CFD=CDF,则ABC的度数为( )
A. B.
C. D.
如图所示,在ABC中,AD平分BAC且与BC相交于点D,B=,BAD=,则C的度数是( )
A. B.
C. D.
已知AD是ABC的一条高,BAD=,CAD=,则BAC的度数为( )
A. B. C. D. 或
如图,用三角尺作ABC的边AB上的高线,下列三角尺的摆放位置正确的是( )
A. B. C. D.
下列说法错误的是( )
A. 三角形的三条中线都能平分三角形的面积
B. 三角形的三条角平分线交于三角形内一点
C. 三角形的三条高交于一点
D. 三角形的中线、角平分线、高都是线段
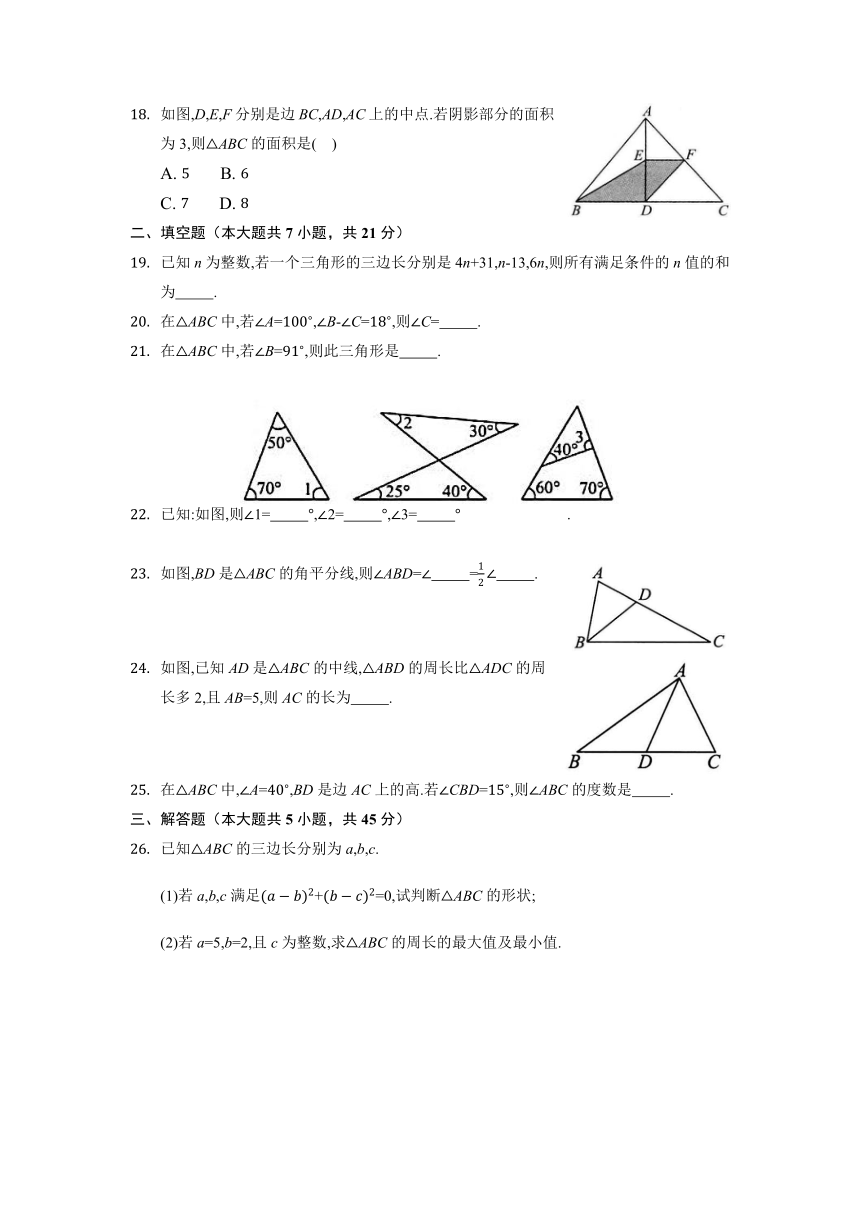
如图,D,E,F分别是边BC,AD,AC上的中点.若阴影部分的面积为3,则ABC的面积是( )
A. B.
C. D.
二、填空题(本大题共7小题,共21分)
已知n为整数,若一个三角形的三边长分别是4n+31,n-13,6n,则所有满足条件的n值的和为 .
在ABC中,若A=,B-C=,则C= .
在ABC中,若B=,则此三角形是 .
已知:如图,则1= ,2= ,3= .
如图,BD是ABC的角平分线,则ABD= = .
如图,已知AD是ABC的中线,ABD的周长比ADC的周长多2,且AB=5,则AC的长为 .
在ABC中,A=,BD是边AC上的高.若CBD=,则ABC的度数是 .
三、解答题(本大题共5小题,共45分)
已知ABC的三边长分别为a,b,c.
(1)若a,b,c满足+=0,试判断ABC的形状;
(2)若a=5,b=2,且c为整数,求ABC的周长的最大值及最小值.
如图,点D是ABC内一点.试说明:
(1)BD+CD< AB+AC;
(2) AD+BD+CD< AB+BC+AC.
在ABC和DEF中,A=,E+F=,将DEF放置在ABC上,使得D的两条边DE,DF分别经过点B,C.
(1)当将DEF如图放置在ABC上时,求ABD+ACD的大小;
(2)当将DEF如图放置在ABC上时,求ABD+ACD的大小.
在ABC中,AB=AC,AC边上的中线BD把ABC的周长分为24 cm和30 cm的两部分,求ABC各边的长.
30.(1)如图,在ABC中,C=,B=,ADBC于点D,AE平分BAC,求EAD的度数;
(2)如果把(1)题中的“C=,B=”改为“C>B”,其他条件不变,请你求出EAD与B,C之间的关系.
1.【答案】D
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】A
13.【答案】C
14.【答案】B
15.【答案】D
16.【答案】B
17.【答案】C
18.【答案】D
19.【答案】48
20.【答案】
21.【答案】钝角三角形
22.【答案】60
35
90
23.【答案】CBD
ABC
24.【答案】3
25.【答案】或
26.【答案】(1)等边三角形
(2)ABC的周长的最大值为13,最小值为11
27.【答案】解:(1)延长BD交AC于点E,
在ABE中,AB+AE>BE.
在EDC中,ED+EC>CD.
所以AB+AE+ED+EC>BE+CD.
因为AE+EC=AC,BE=BD+DE,
所以AB+AC+ED>BD+DE+CD.
所以BD+CD< AB+AC.
(2)由(1)同理可得AB+BC>AD+CD,BC+AC>BD+AD,
又因为AB+AC>BD+CD,
所以2(AD+BD+CD)<2(AB+BC+AC).
所以AD+BD+CD< AB+BC+AC.
28.【答案】解:(1)由题意可知D=-=.
所以DBC+DCB=-D=.
又因为ABC+ACB=-A=,
所以ABD+ACD=(ABC+DBC)+(ACB+DCB)=.
(2)因为在ABC中,A=,
所以ABC+ACB=.
因为在DEF中,E+F=,所以D=,
所以BCD+CBD=-D=,
所以ABD+ACD=(ABC+ACB)-(BCD+CBD)=-=.
29.【答案】解:三角形各边的长有两种情况:
AB=AC=16 cm,BC=22 cm;
AB=AC=20 cm,BC=14 cm.
30.【答案】解:(1)因为AE平分BAC,
所以EAC=BAC.
因为BAC=-B-C=--=,
所以EAC=.
因为ADBC,
所以ADC=.
所以DAC=-ADC-C=--=.
所以EAD=EAC-DAC=-=.
(2)因为AE平分BAC,
所以EAC=BAC=(-B-C)=-B-C.
因为ADBC,
所以ADC=.
所以DAC=-ADC-C=-C.
所以EAD=EAC-DAC=-B-C-(-C)= -B-C-+C=(C-B).
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共18小题,共54分)
三角形按边分类可分为( )
A. 不等边三角形、等边三角形
B. 等腰三角形、等边三角形
C. 不等边三角形、等腰三角形、等边三角形
D. 不等边三角形、等腰三角形
在课堂上,老师在黑板上画出了如图所示的三个三角形,让同学们根据它们的边长进行分类,其中说法错误的是( )
A. 是不等边三角形 B. 是等腰三角形
C. 是等边三角形 D. 是等边三角形
设三角形三边之长分别为3,8,1-2a,则a的取值范围为( )
A. B.
C. D. 或
长度分别为8,6,6,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A. B. C. D.
已知a,b,c是ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )
A. B. C. D.
已知等腰三角形一边长为4,另一边长为8,则这个等腰三角形的周长为( )
A. B. 或 C. D.
长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )
A. B. C. D.
已知ABC是锐角三角形,A=,则B的度数可以是( )
A. B. C. D.
在ABC中,A比B大,则ABC的形状是( )
A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 无法判断
在ABC中,如果A+B+2C=,那么ABC是( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 锐角三角形或钝角三角形
如图,在ABC中,B=,MNAC,1=,则C的度数是( )
A. B.
C. D.
如图,在RtABC中,ACB=,点D在AB边上,将CBD沿CD折叠,使点B恰好落在AC边上的点E处.若A=,则CDE的度数是( )
A. B. C. D.
如图,在ABC中,EFD=,且AEF=AFE,CFD=CDF,则ABC的度数为( )
A. B.
C. D.
如图所示,在ABC中,AD平分BAC且与BC相交于点D,B=,BAD=,则C的度数是( )
A. B.
C. D.
已知AD是ABC的一条高,BAD=,CAD=,则BAC的度数为( )
A. B. C. D. 或
如图,用三角尺作ABC的边AB上的高线,下列三角尺的摆放位置正确的是( )
A. B. C. D.
下列说法错误的是( )
A. 三角形的三条中线都能平分三角形的面积
B. 三角形的三条角平分线交于三角形内一点
C. 三角形的三条高交于一点
D. 三角形的中线、角平分线、高都是线段
如图,D,E,F分别是边BC,AD,AC上的中点.若阴影部分的面积为3,则ABC的面积是( )
A. B.
C. D.
二、填空题(本大题共7小题,共21分)
已知n为整数,若一个三角形的三边长分别是4n+31,n-13,6n,则所有满足条件的n值的和为 .
在ABC中,若A=,B-C=,则C= .
在ABC中,若B=,则此三角形是 .
已知:如图,则1= ,2= ,3= .
如图,BD是ABC的角平分线,则ABD= = .
如图,已知AD是ABC的中线,ABD的周长比ADC的周长多2,且AB=5,则AC的长为 .
在ABC中,A=,BD是边AC上的高.若CBD=,则ABC的度数是 .
三、解答题(本大题共5小题,共45分)
已知ABC的三边长分别为a,b,c.
(1)若a,b,c满足+=0,试判断ABC的形状;
(2)若a=5,b=2,且c为整数,求ABC的周长的最大值及最小值.
如图,点D是ABC内一点.试说明:
(1)BD+CD< AB+AC;
(2) AD+BD+CD< AB+BC+AC.
在ABC和DEF中,A=,E+F=,将DEF放置在ABC上,使得D的两条边DE,DF分别经过点B,C.
(1)当将DEF如图放置在ABC上时,求ABD+ACD的大小;
(2)当将DEF如图放置在ABC上时,求ABD+ACD的大小.
在ABC中,AB=AC,AC边上的中线BD把ABC的周长分为24 cm和30 cm的两部分,求ABC各边的长.
30.(1)如图,在ABC中,C=,B=,ADBC于点D,AE平分BAC,求EAD的度数;
(2)如果把(1)题中的“C=,B=”改为“C>B”,其他条件不变,请你求出EAD与B,C之间的关系.
1.【答案】D
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】A
11.【答案】B
12.【答案】A
13.【答案】C
14.【答案】B
15.【答案】D
16.【答案】B
17.【答案】C
18.【答案】D
19.【答案】48
20.【答案】
21.【答案】钝角三角形
22.【答案】60
35
90
23.【答案】CBD
ABC
24.【答案】3
25.【答案】或
26.【答案】(1)等边三角形
(2)ABC的周长的最大值为13,最小值为11
27.【答案】解:(1)延长BD交AC于点E,
在ABE中,AB+AE>BE.
在EDC中,ED+EC>CD.
所以AB+AE+ED+EC>BE+CD.
因为AE+EC=AC,BE=BD+DE,
所以AB+AC+ED>BD+DE+CD.
所以BD+CD< AB+AC.
(2)由(1)同理可得AB+BC>AD+CD,BC+AC>BD+AD,
又因为AB+AC>BD+CD,
所以2(AD+BD+CD)<2(AB+BC+AC).
所以AD+BD+CD< AB+BC+AC.
28.【答案】解:(1)由题意可知D=-=.
所以DBC+DCB=-D=.
又因为ABC+ACB=-A=,
所以ABD+ACD=(ABC+DBC)+(ACB+DCB)=.
(2)因为在ABC中,A=,
所以ABC+ACB=.
因为在DEF中,E+F=,所以D=,
所以BCD+CBD=-D=,
所以ABD+ACD=(ABC+ACB)-(BCD+CBD)=-=.
29.【答案】解:三角形各边的长有两种情况:
AB=AC=16 cm,BC=22 cm;
AB=AC=20 cm,BC=14 cm.
30.【答案】解:(1)因为AE平分BAC,
所以EAC=BAC.
因为BAC=-B-C=--=,
所以EAC=.
因为ADBC,
所以ADC=.
所以DAC=-ADC-C=--=.
所以EAD=EAC-DAC=-=.
(2)因为AE平分BAC,
所以EAC=BAC=(-B-C)=-B-C.
因为ADBC,
所以ADC=.
所以DAC=-ADC-C=-C.
所以EAD=EAC-DAC=-B-C-(-C)= -B-C-+C=(C-B).
第2页,共2页
