2021-2022学年高一上学期数学苏教版(2019)必修第一册第八章 函数应用 期末培优卷(Word含答案解析)
文档属性
| 名称 | 2021-2022学年高一上学期数学苏教版(2019)必修第一册第八章 函数应用 期末培优卷(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 22:08:35 | ||
图片预览




文档简介
2021-2022学年高一(上)必修第一册数学(苏教版2019)
第八章 函数应用 期末培优卷
一、单选题。本大题共8小题,每小题5分,共40分,每小题只有一个选项符合题意。
1.若关于x的方程有解,则实数a的取值范围是( )
A.[0,1) B.[1,2) C.[1,+∞) D.(2,+∞)
2.对于函数,若存在,使,则称点与点是函数的一对“隐对称点”.若函数的图象存在“隐对称点”,则实数的取值范围是( )
A. B. C. D.
3.已知函数,其中,若方程有四个不同的实根、、、,则的取值范围是( )
A. B. C. D.
4.已知的值域为,则实数( )
A.4或0 B.4或 C.0或 D.2或
5.已知函数,下列是关于函数的零点个数的判断,其中正确的是( )
A.当时,有3个零点 B.当时,有2个零点
C.当时,有4个零点 D.当时,有3个零点
6.已知函数有唯一的零点,则的值为( )
A. B. C. D.
7.函数,若函数有3个不同的零点,,,则的取值范围是( )
A. B. C. D.
8.如图,点P在边长为1的正方形的边上运动,M是CD的中点,则当点P沿着路径A—B—C—M(不包含A,M点)运动时,△APM的面积y关于点P经过的路程x的函数y=f(x)的图像的大致形状为( )
A. B.
C. D.
二、多选题。本大题共4小题,每小题5分,共20分,每小题有两项或以上符合题意。
9.已知函数,实数a,b,c满足,且,若实数是函数f(x)的一个零点,则下列结论可能成立的是( )
A. B. C. D.
10.已知函数若方程有三个实数根,且,则下列结论正确的为( )
A. B.的取值范围为
C.的取值范围为 D.不等式的解集为
11.某辆汽车以的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求)时,每小时的油耗(所需要的汽油量)为,其中为常数.若汽车以120km/h的速度行驶时,每小时的油耗为,欲使每小时的油耗不超过,则速度x的值可为( )
A.60 B.80 C.100 D.120
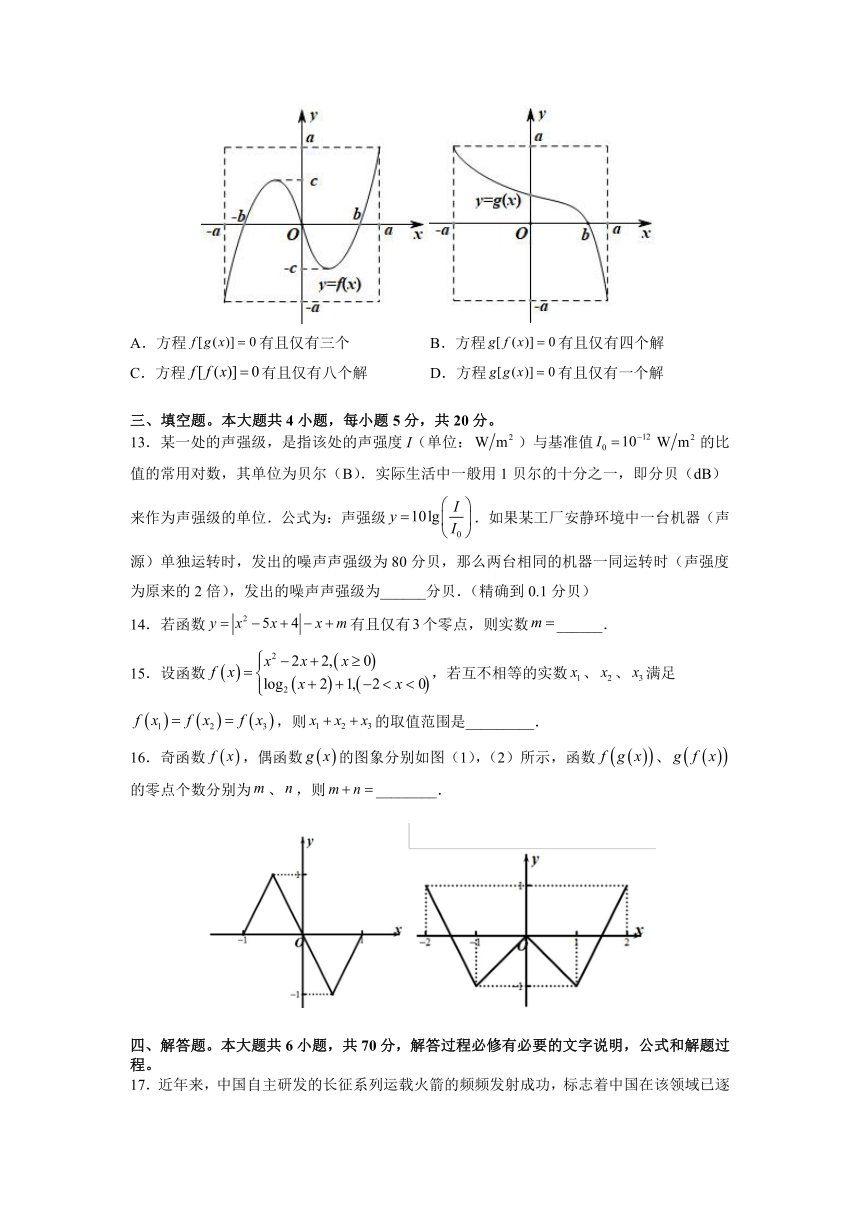
12.定义域和值域均为的函数和的图象如图所示,其中,给出下列四个结论正确结论的是( )
A.方程有且仅有三个 B.方程有且仅有四个解
C.方程有且仅有八个解 D.方程有且仅有一个解
三、填空题。本大题共4小题,每小题5分,共20分。
13.某一处的声强级,是指该处的声强度I(单位:)与基准值的比值的常用对数,其单位为贝尔(B).实际生活中一般用1贝尔的十分之一,即分贝(dB)来作为声强级的单位.公式为:声强级.如果某工厂安静环境中一台机器(声源)单独运转时,发出的噪声声强级为80分贝,那么两台相同的机器一同运转时(声强度为原来的2倍),发出的噪声声强级为______分贝.(精确到0.1分贝)
14.若函数有且仅有个零点,则实数______.
15.设函数,若互不相等的实数、、满足,则的取值范围是_________.
16.奇函数,偶函数的图象分别如图(1),(2)所示,函数、的零点个数分别为、,则________.
四、解答题。本大题共6小题,共70分,解答过程必修有必要的文字说明,公式和解题过程。
17.近年来,中国自主研发的长征系列运载火箭的频频发射成功,标志着中国在该领域已逐步达到世界一流水平.设火箭推进剂的质量为M(单位:t),去除推进剂后的火箭有效载荷质量为m(单位:t),火箭的飞行速度为v(单位:),初始速度为(单位:),已知其关系式为齐奥尔科夫斯基公式:,其中是火箭发动机喷流相对火箭的速度.假设,,
(参考数据:,,,).
(1)若,当火箭飞行速度分别达到第一宇宙速度()、第二宇宙速度()、第三宇宙速度()时,求相应的M;(精确到小数点后一位)
(2)如果希望火箭飞行速度达到,但火箭起飞质量的最大值为,请问的最小值为多少?(精确到小数点后一位)
18.设函数.
(1)当时,解不等式;
(2)若,且关于的方程在[-2,6]上有实数解,求实数的取值范围.
19.已知函数,其中均为实数.
(I)若,求的范围;
(Ⅱ)若函数存在零点且,求的最小值.
20.已知函数.
(1)若函数在区间上有两个相异的零点,求实数的取值范围;
(2)若函数在区间上的最小值为0,求实数的值.
21.已知函数其中.
(1)当a=0时,求f(x)的值域;
(2)若f(x)有两个零点,求a的取值范围.
22.已知函数的图象过点.
Ⅰ判断函数的奇偶性并求其值域;
Ⅱ若关于x的方程在上有解,求实数t的取值范围.
参考答案
1.B
【解析】解: 有解等价于有解,
由于,所以,所以
所以,
则实数a的取值范围是[1,2).
故选:B.
2.B
【解析】解:由隐对称点的定义可知函数图象上存在关于原点对称的点
设的图象与函数,的图象关于原点对称
令,则,
故原题义等价于方程有零点,解得
又因为,当且仅当时取等号
.
故选:B.
3.B
【解析】由,可得,,可得,即,
所以,,作出函数的图象如下图所示:
因为方程有四个不同的实根,则,解得,
由已知可得、是方程的两根,则,
满足,可得,
满足,可得,
因此,,
当时,随着的增大而增大,则,
因此,.
故选:B.
4.B
【解析】解:由,
由,可得,或,或,
它的定义域为,值域为,
若,则,则函数的值域为,不满足条件.
若,则根据函数的定义域为,
此时,函数的零点为,,
若,当时,不满足题意.
若,当时,不满足题意.
所以,求得;
若,则函数的定义域为,
此时函数的零点为,,
同理可得,所以.
综上,或,
故选:B.
5.C
【解析】由题意可知,,
当时:若,则,
①时,有,解得;
②时,有,解得,
若,则,
①时,有,解得,
②时,有,解得,
故当时,有4个零点,C正确,
当时:若,则,有,解得,
因为,所以不满足,舍去;
若,则,
①时,有,无解;
②时,有,解得,
故当时,有1个零点,D错误
故选:C
6.B
【解析】,
所以,,
所以,函数的图象关于直线对称,
若,则函数的零点必成对出现,即函数的零点个数为偶数,不合乎题意.
由于函数有唯一零点,则,解得.
故选:B.
7.D
【解析】作出函数的图象,如图,作直线,只有当时,它们才可能是三个交点,
不妨设,则,所以,而,,
所以.
故选:D.
8.A
【解析】根据题意,当时,;
当时,,即
;
当时,
整理得y=f(x)=观察图像,A项合理.
故选:A.
9.ABC
【解析】函数定义域为,且在上单调递增,而,则,
因,则有中一个为负,两个为正或者三个都为负,
即或,而是函数f(x)的一个零点,即,
于是得或,因此,或,
所以只有不可能,一定有成立,,可能成立.
故选:ABC
10.ACD
【解析】方程的争即为函数的图象与直线的交点的横坐标,作出函数的图象和直线,如图,由图可知:,
,,A正确;
由于,∴,B错误;
由得,∴,∴,C正确;
由,时,,,时,,,
综上,D正确.
故选:ACD.
11.ABC
【解析】由汽车以120km/h的速度行驶时,每小时的油耗为,
,解得:,故每小时油耗为,
由题意得,解得:,
又,故,所以速度的取值范围为.
故选:ABC
12.AD
【解析】对于A中,设,则由,即,
当时,则有三个不同的值,
由于是减函数,所以有三个解,所以A正确;
对于B中,设,则由,即,解得,
因为,所以只有3个解,所以B不正确;
对于C中,设,若,即,
当或或,则或或,
因为,所以每个方程对应着3个根,所以共有9个解,所以C错误;
对于D中,设,若,即,所以,
因为是减函数,所以方程只有1解,所以D正确.
故选:AD
13.83.0.
【解析】根据题意,,则两台相同的机器一同运转时,发出的噪声声强级为(分贝)
故答案为:83.0.
14.或
【解析】令,
因为函数有且仅有个零点,所以函数与函数的图象共有个公共点,
当时,即当或时,,
当时,即当时,,
作出函数与函数的图象如下图所示,
由图可知,当或时,函数与函数的图象共有个公共点,
即有且仅有个零点.
故答案为:或.
15.
【解析】作出函数的图象,设,如下图所示:
二次函数的图象关于直线对称,则,
由图可得,可得,解得,
所以,.
故答案为:.
16.10
【解析】由题中函数图象知,,,,,,
所以,,,,
所以有个零点,即.
又,,
所以有个零点,即,因此,.
故答案为:.
17.
(1)答案见解析
(2)
(1)
由题意知:.
当时有,则;
当时有,则;
当时有,则.
(2)
∵希望火箭飞行速度达到,但火箭起飞质的最大值为,,
∴,,,
∴,即,得,
∴的最小值为.
18.(1);(2).
【解析】(1)由题意,知,则
由得或,由得,
所以,原不等式的解集为
(2),
即
因为在上是增函数,在上减函数,
所以函数在上是增函数,
所以时,;时,,
所以,实数的取值范围是.
19.(I);(Ⅱ)
【解析】解:(I)因为,,
可得,
即为,
解得,则,
由,得,
即,
则;
故的取值范围为
(Ⅱ)因为存在零点,故设,显然,因为;
所以,所以,所以,当且仅当,即时取等号,又,所以
所以
20.(1);(2).
【解析】解:(1)方法一:依题意可得,
∴,
∴;
方法二:由,
令,设,
∵
,
若,则,即,又,
∴,即在上单调递减,
若,同理可得在上单调递增,
∵,,
∴要使在上有两个零点,只需;
(2)∵,
①当即时,在区间的最小值为,
依题意有,即(舍);
②当即时,在区间的最小值为,
根据题意有,即;
③当即时,在区间的最小值为,
根据题意有,即(舍);
综上:实数的值为;
21.(1);(2)
【解析】(1)当时,,
则当时,,
当时,单调递增,则,
综上,的值域为;
(2)当时,,当时,单调递增,
若,有1个零点,则,则时,也应有1个零点,所以,又,则;
若,无零点,则,则时,有2个零点,所以;
综上,a的取值范围为.
22.(Ⅰ); (Ⅱ).
【解析】函数的图象过点
即:
(Ⅰ)
则的定义域为,关于原点对称
且
故为偶函数
又由
故,即和值域为
(Ⅱ)若关于的方程在上有解
即,即在上有解
即在上有解
由对勾函数的图象和性质可得:
当时,取最小值;当或时,取最大值
故实数的取值范围是
第八章 函数应用 期末培优卷
一、单选题。本大题共8小题,每小题5分,共40分,每小题只有一个选项符合题意。
1.若关于x的方程有解,则实数a的取值范围是( )
A.[0,1) B.[1,2) C.[1,+∞) D.(2,+∞)
2.对于函数,若存在,使,则称点与点是函数的一对“隐对称点”.若函数的图象存在“隐对称点”,则实数的取值范围是( )
A. B. C. D.
3.已知函数,其中,若方程有四个不同的实根、、、,则的取值范围是( )
A. B. C. D.
4.已知的值域为,则实数( )
A.4或0 B.4或 C.0或 D.2或
5.已知函数,下列是关于函数的零点个数的判断,其中正确的是( )
A.当时,有3个零点 B.当时,有2个零点
C.当时,有4个零点 D.当时,有3个零点
6.已知函数有唯一的零点,则的值为( )
A. B. C. D.
7.函数,若函数有3个不同的零点,,,则的取值范围是( )
A. B. C. D.
8.如图,点P在边长为1的正方形的边上运动,M是CD的中点,则当点P沿着路径A—B—C—M(不包含A,M点)运动时,△APM的面积y关于点P经过的路程x的函数y=f(x)的图像的大致形状为( )
A. B.
C. D.
二、多选题。本大题共4小题,每小题5分,共20分,每小题有两项或以上符合题意。
9.已知函数,实数a,b,c满足,且,若实数是函数f(x)的一个零点,则下列结论可能成立的是( )
A. B. C. D.
10.已知函数若方程有三个实数根,且,则下列结论正确的为( )
A. B.的取值范围为
C.的取值范围为 D.不等式的解集为
11.某辆汽车以的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求)时,每小时的油耗(所需要的汽油量)为,其中为常数.若汽车以120km/h的速度行驶时,每小时的油耗为,欲使每小时的油耗不超过,则速度x的值可为( )
A.60 B.80 C.100 D.120
12.定义域和值域均为的函数和的图象如图所示,其中,给出下列四个结论正确结论的是( )
A.方程有且仅有三个 B.方程有且仅有四个解
C.方程有且仅有八个解 D.方程有且仅有一个解
三、填空题。本大题共4小题,每小题5分,共20分。
13.某一处的声强级,是指该处的声强度I(单位:)与基准值的比值的常用对数,其单位为贝尔(B).实际生活中一般用1贝尔的十分之一,即分贝(dB)来作为声强级的单位.公式为:声强级.如果某工厂安静环境中一台机器(声源)单独运转时,发出的噪声声强级为80分贝,那么两台相同的机器一同运转时(声强度为原来的2倍),发出的噪声声强级为______分贝.(精确到0.1分贝)
14.若函数有且仅有个零点,则实数______.
15.设函数,若互不相等的实数、、满足,则的取值范围是_________.
16.奇函数,偶函数的图象分别如图(1),(2)所示,函数、的零点个数分别为、,则________.
四、解答题。本大题共6小题,共70分,解答过程必修有必要的文字说明,公式和解题过程。
17.近年来,中国自主研发的长征系列运载火箭的频频发射成功,标志着中国在该领域已逐步达到世界一流水平.设火箭推进剂的质量为M(单位:t),去除推进剂后的火箭有效载荷质量为m(单位:t),火箭的飞行速度为v(单位:),初始速度为(单位:),已知其关系式为齐奥尔科夫斯基公式:,其中是火箭发动机喷流相对火箭的速度.假设,,
(参考数据:,,,).
(1)若,当火箭飞行速度分别达到第一宇宙速度()、第二宇宙速度()、第三宇宙速度()时,求相应的M;(精确到小数点后一位)
(2)如果希望火箭飞行速度达到,但火箭起飞质量的最大值为,请问的最小值为多少?(精确到小数点后一位)
18.设函数.
(1)当时,解不等式;
(2)若,且关于的方程在[-2,6]上有实数解,求实数的取值范围.
19.已知函数,其中均为实数.
(I)若,求的范围;
(Ⅱ)若函数存在零点且,求的最小值.
20.已知函数.
(1)若函数在区间上有两个相异的零点,求实数的取值范围;
(2)若函数在区间上的最小值为0,求实数的值.
21.已知函数其中.
(1)当a=0时,求f(x)的值域;
(2)若f(x)有两个零点,求a的取值范围.
22.已知函数的图象过点.
Ⅰ判断函数的奇偶性并求其值域;
Ⅱ若关于x的方程在上有解,求实数t的取值范围.
参考答案
1.B
【解析】解: 有解等价于有解,
由于,所以,所以
所以,
则实数a的取值范围是[1,2).
故选:B.
2.B
【解析】解:由隐对称点的定义可知函数图象上存在关于原点对称的点
设的图象与函数,的图象关于原点对称
令,则,
故原题义等价于方程有零点,解得
又因为,当且仅当时取等号
.
故选:B.
3.B
【解析】由,可得,,可得,即,
所以,,作出函数的图象如下图所示:
因为方程有四个不同的实根,则,解得,
由已知可得、是方程的两根,则,
满足,可得,
满足,可得,
因此,,
当时,随着的增大而增大,则,
因此,.
故选:B.
4.B
【解析】解:由,
由,可得,或,或,
它的定义域为,值域为,
若,则,则函数的值域为,不满足条件.
若,则根据函数的定义域为,
此时,函数的零点为,,
若,当时,不满足题意.
若,当时,不满足题意.
所以,求得;
若,则函数的定义域为,
此时函数的零点为,,
同理可得,所以.
综上,或,
故选:B.
5.C
【解析】由题意可知,,
当时:若,则,
①时,有,解得;
②时,有,解得,
若,则,
①时,有,解得,
②时,有,解得,
故当时,有4个零点,C正确,
当时:若,则,有,解得,
因为,所以不满足,舍去;
若,则,
①时,有,无解;
②时,有,解得,
故当时,有1个零点,D错误
故选:C
6.B
【解析】,
所以,,
所以,函数的图象关于直线对称,
若,则函数的零点必成对出现,即函数的零点个数为偶数,不合乎题意.
由于函数有唯一零点,则,解得.
故选:B.
7.D
【解析】作出函数的图象,如图,作直线,只有当时,它们才可能是三个交点,
不妨设,则,所以,而,,
所以.
故选:D.
8.A
【解析】根据题意,当时,;
当时,,即
;
当时,
整理得y=f(x)=观察图像,A项合理.
故选:A.
9.ABC
【解析】函数定义域为,且在上单调递增,而,则,
因,则有中一个为负,两个为正或者三个都为负,
即或,而是函数f(x)的一个零点,即,
于是得或,因此,或,
所以只有不可能,一定有成立,,可能成立.
故选:ABC
10.ACD
【解析】方程的争即为函数的图象与直线的交点的横坐标,作出函数的图象和直线,如图,由图可知:,
,,A正确;
由于,∴,B错误;
由得,∴,∴,C正确;
由,时,,,时,,,
综上,D正确.
故选:ACD.
11.ABC
【解析】由汽车以120km/h的速度行驶时,每小时的油耗为,
,解得:,故每小时油耗为,
由题意得,解得:,
又,故,所以速度的取值范围为.
故选:ABC
12.AD
【解析】对于A中,设,则由,即,
当时,则有三个不同的值,
由于是减函数,所以有三个解,所以A正确;
对于B中,设,则由,即,解得,
因为,所以只有3个解,所以B不正确;
对于C中,设,若,即,
当或或,则或或,
因为,所以每个方程对应着3个根,所以共有9个解,所以C错误;
对于D中,设,若,即,所以,
因为是减函数,所以方程只有1解,所以D正确.
故选:AD
13.83.0.
【解析】根据题意,,则两台相同的机器一同运转时,发出的噪声声强级为(分贝)
故答案为:83.0.
14.或
【解析】令,
因为函数有且仅有个零点,所以函数与函数的图象共有个公共点,
当时,即当或时,,
当时,即当时,,
作出函数与函数的图象如下图所示,
由图可知,当或时,函数与函数的图象共有个公共点,
即有且仅有个零点.
故答案为:或.
15.
【解析】作出函数的图象,设,如下图所示:
二次函数的图象关于直线对称,则,
由图可得,可得,解得,
所以,.
故答案为:.
16.10
【解析】由题中函数图象知,,,,,,
所以,,,,
所以有个零点,即.
又,,
所以有个零点,即,因此,.
故答案为:.
17.
(1)答案见解析
(2)
(1)
由题意知:.
当时有,则;
当时有,则;
当时有,则.
(2)
∵希望火箭飞行速度达到,但火箭起飞质的最大值为,,
∴,,,
∴,即,得,
∴的最小值为.
18.(1);(2).
【解析】(1)由题意,知,则
由得或,由得,
所以,原不等式的解集为
(2),
即
因为在上是增函数,在上减函数,
所以函数在上是增函数,
所以时,;时,,
所以,实数的取值范围是.
19.(I);(Ⅱ)
【解析】解:(I)因为,,
可得,
即为,
解得,则,
由,得,
即,
则;
故的取值范围为
(Ⅱ)因为存在零点,故设,显然,因为;
所以,所以,所以,当且仅当,即时取等号,又,所以
所以
20.(1);(2).
【解析】解:(1)方法一:依题意可得,
∴,
∴;
方法二:由,
令,设,
∵
,
若,则,即,又,
∴,即在上单调递减,
若,同理可得在上单调递增,
∵,,
∴要使在上有两个零点,只需;
(2)∵,
①当即时,在区间的最小值为,
依题意有,即(舍);
②当即时,在区间的最小值为,
根据题意有,即;
③当即时,在区间的最小值为,
根据题意有,即(舍);
综上:实数的值为;
21.(1);(2)
【解析】(1)当时,,
则当时,,
当时,单调递增,则,
综上,的值域为;
(2)当时,,当时,单调递增,
若,有1个零点,则,则时,也应有1个零点,所以,又,则;
若,无零点,则,则时,有2个零点,所以;
综上,a的取值范围为.
22.(Ⅰ); (Ⅱ).
【解析】函数的图象过点
即:
(Ⅰ)
则的定义域为,关于原点对称
且
故为偶函数
又由
故,即和值域为
(Ⅱ)若关于的方程在上有解
即,即在上有解
即在上有解
由对勾函数的图象和性质可得:
当时,取最小值;当或时,取最大值
故实数的取值范围是
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
