黑龙江省哈尔滨市第六十九中学校2021--2022学年九年级 上学期 期中学情检测 数学试卷(word版含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市第六十九中学校2021--2022学年九年级 上学期 期中学情检测 数学试卷(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 10:27:29 | ||
图片预览


文档简介
哈尔滨市第六十九中学学情自我监测
九年级 数学
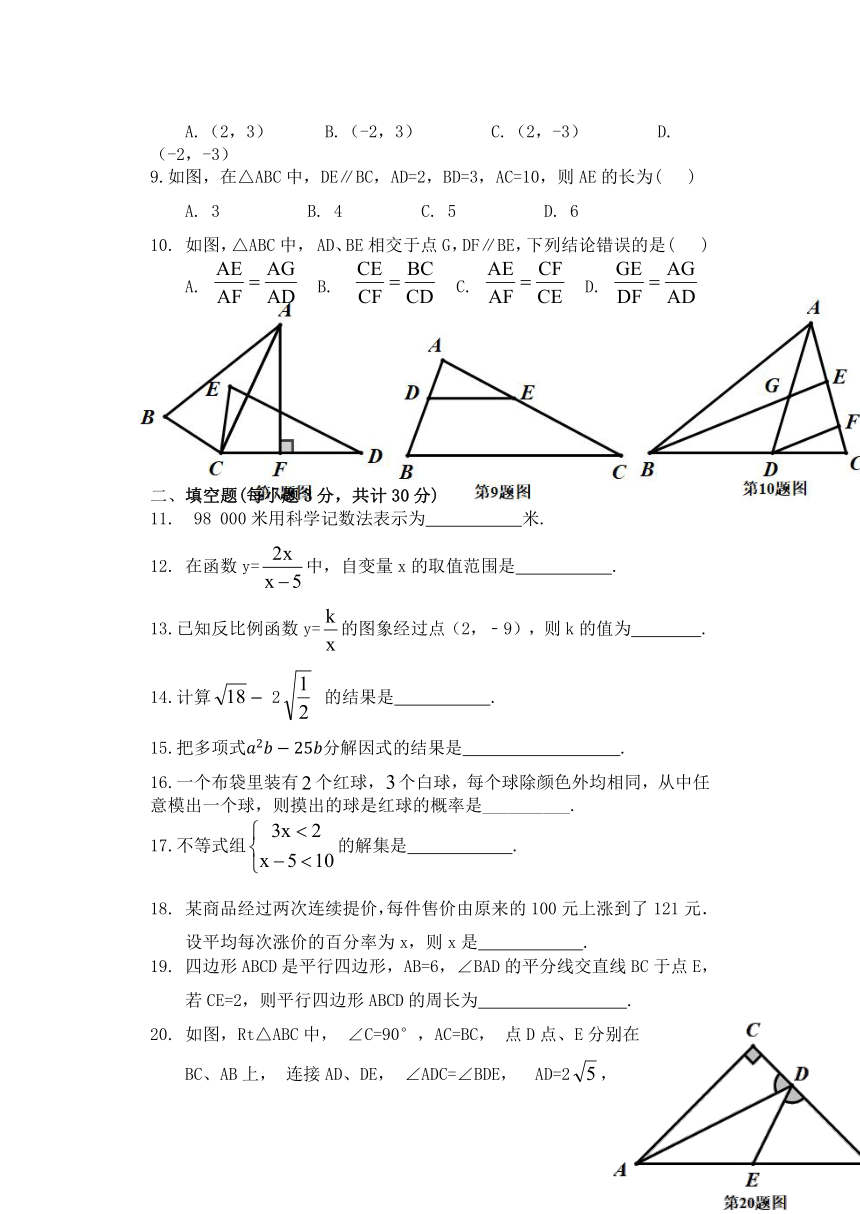
选择题(每小题3分,共30分)
1. -6的相反数是( )
A. 6 B. 6 C. D.
2.下列运算一定正确的是( )
A. B. C. D.
3.下列图形中是中心对称图形但不是轴对称图形的是( )
A B C D
下图是由4个相同的正方体组成的立体图形,它的左视图是( )
如图,AC是⊙O直径,BC⊥AC于C, 连接AB交⊙O
于D,连接CD, AC=8,tan∠BCD=, 则AB长为( )
A. 8 B. 7 C. 10 D. 6
6.分式方程的解为( )
A. x=5 B. x=3 C. x=1 D. x=2
7.如图△ABC≌△DEC,点A和点D是对应顶点,当B和点E是对应顶点,
过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A. 30° B. 25° C. 35° D. 65°
8.抛物线的顶点坐标为( )
A.(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
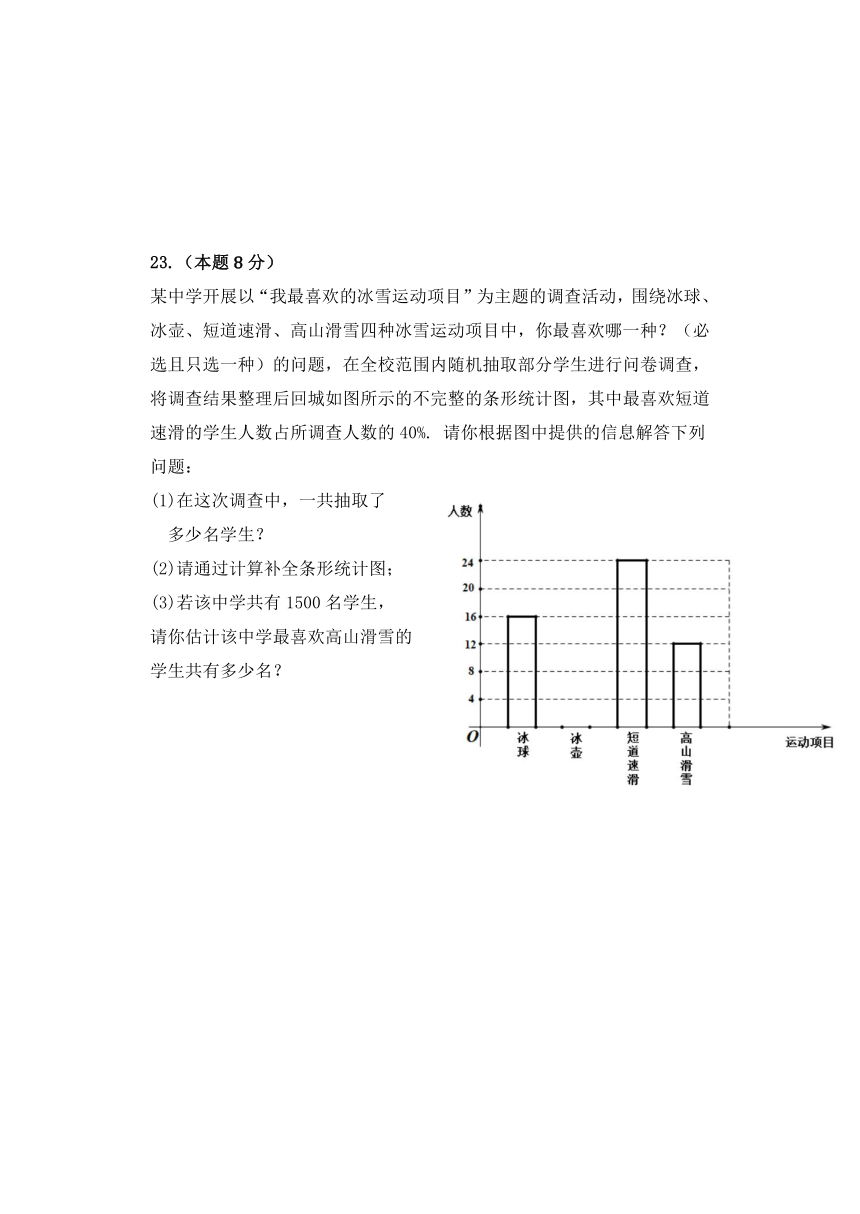
9.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A. 3 B. 4 C. 5 D. 6
如图,△ABC中, AD、BE相交于点G,DF∥BE,下列结论错误的是( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11. 98 000米用科学记数法表示为 米.
12. 在函数y=中,自变量x的取值范围是 .
13.已知反比例函数y=的图象经过点(2,﹣9),则k的值为 .
14.计算 2 的结果是 .
15.把多项式分解因式的结果是 .
16.一个布袋里装有个红球,个白球,每个球除颜色外均相同,从中任意模出一个球,则摸出的球是红球的概率是__________.
17.不等式组的解集是 .
18. 某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.
设平均每次涨价的百分率为x,则x是 .
19. 四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E,
若CE=2,则平行四边形ABCD的周长为 .
20. 如图,Rt△ABC中, ∠C=90°,AC=BC, 点D点、E分别在
BC、AB上, 连接AD、DE, ∠ADC=∠BDE, AD=2,
DE=, 则AE= .
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.(本题7分)
先化简,再求代数式的值,其中a =2sin45°﹣1.
22.(本题7分)
如图,方格中每个小正方形的边长为1个单位长度,△ABC的顶点和线段DE的端点均在小正方形的顶点上.
(1)在方格纸中将△ABC向上平移1个单位长度,再向右平移2个单位长度后得到△MNP(点A的对应点是M,点B的对应点是点N,点C的对应点是点P),请画出△MNP;
(2)在方格纸中画出以DE为斜边的等腰
直角三角形DEF(点F在小正方形的顶点上)
.连接FP,请直接写出线段FP的长.
23.(本题8分)
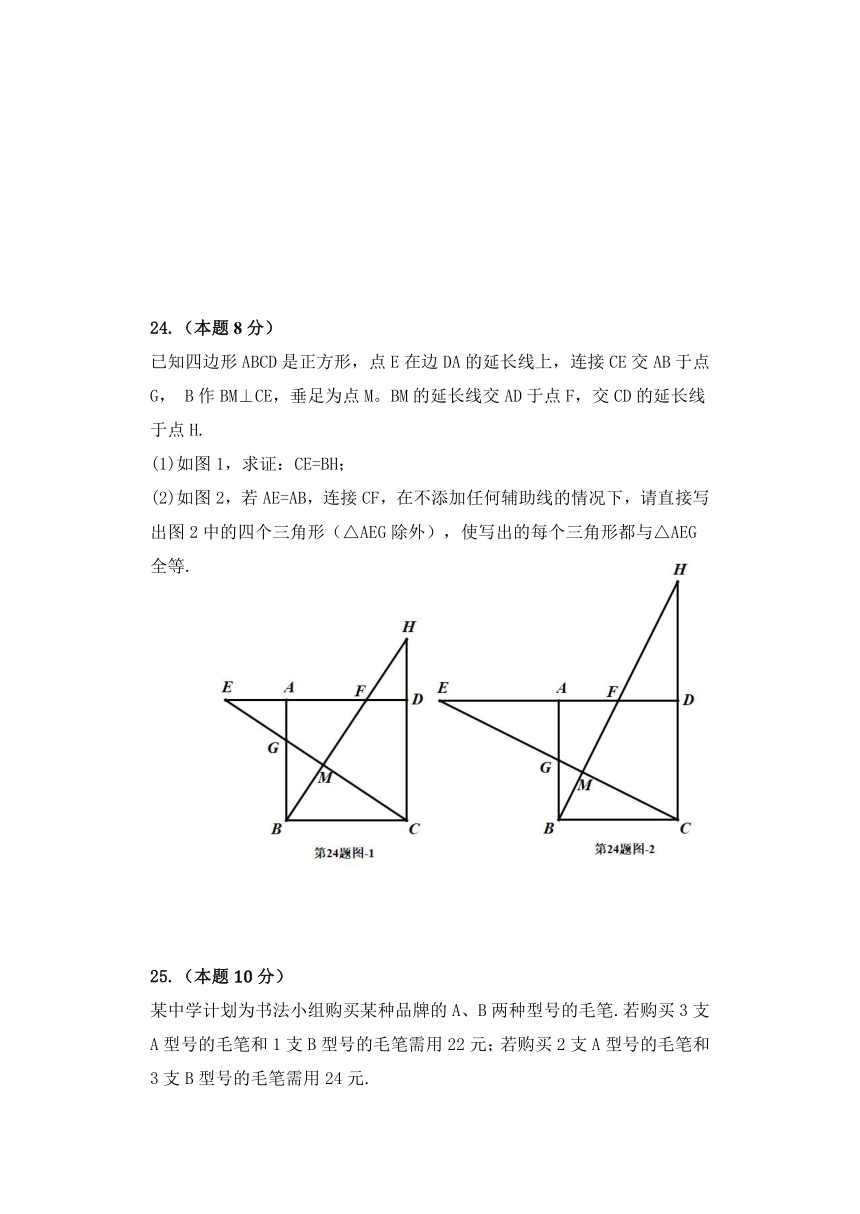
某中学开展以“我最喜欢的冰雪运动项目”为主题的调查活动,围绕冰球、冰壶、短道速滑、高山滑雪四种冰雪运动项目中,你最喜欢哪一种?(必选且只选一种)的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后回城如图所示的不完整的条形统计图,其中最喜欢短道速滑的学生人数占所调查人数的40%. 请你根据图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了
多少名学生?
(2)请通过计算补全条形统计图;
(3)若该中学共有1500名学生,
请你估计该中学最喜欢高山滑雪的
学生共有多少名?
24.(本题8分)
已知四边形ABCD是正方形,点E在边DA的延长线上,连接CE交AB于点G, B作BM⊥CE,垂足为点M。BM的延长线交AD于点F,交CD的延长线于点H.
(1)如图1,求证:CE=BH;
(2)如图2,若AE=AB,连接CF,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(△AEG除外),使写出的每个三角形都与△AEG全等.
25.(本题10分)
某中学计划为书法小组购买某种品牌的A、B两种型号的毛笔.若购买3支A型号的毛笔和1支B型号的毛笔需用22元;若购买2支A型号的毛笔和3支B型号的毛笔需用24元.
(1)求每支A种型号的毛笔和每支B型号的毛笔各是多少元;
(2)该中学决定购买以上两种型号的毛笔共80支,总费用不超过420元,那么该中学最多可以购买多少支A种型号的毛笔?
26.(本题10分)
已知△ABC内接于⊙O,BD为⊙O的直径,连接AD,AC与BD交于点E.
(1)如图1,求证:∠ABD+∠ACB=90°;
(2)如图2,过点A作AG⊥BC,垂足为点G,AG交BD于点F,若EF=ED, 求证:AB=BC;
(3)如图3,在(2)的条件下,过点C作BD的平行线交AG的延长线与点H,交⊙O于点P,
连接BH,若∠BHP=45°,CH=6,求线段BH的长.
27.(本题10分)
如图,在平面直角坐标系中,直线AB的解析式为y=kx+3分别交x轴、y轴于点A、B,∠BAO=45°.
(1)求直线AB的解析式;
(2)点C在y轴负半轴上,连接CB,过点B作BC的垂线交x轴于点P,设点P的横坐标为t,△BAP的面积为S,求S与t之间的函数解析式,(不要求写出自变量t的取值范围) ;
(3)在(2)的条件下,延长BC至Q,使BQ=BP,过点Q作x轴的垂线交x轴于点D,点E为线段CQ的中点,过点E作BQ的垂线交BD的延长线与点F,若EF= , 求Q点坐标.
哈尔滨市第六十九中学学情自我监测
参考答案
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C A C A B D B C
填空题:
11 12 13 14 15
9.8×104 x≠5 18 2 b(a+5)(a-5)
16 17 18 19 20
X< 10% 20或28 3
(1)略;(2)略;(3)
(1)y=-x+3;(2);(3)Q(-3,-6)
下面图形为参考图形
26.
27.
27.
九年级 数学
选择题(每小题3分,共30分)
1. -6的相反数是( )
A. 6 B. 6 C. D.
2.下列运算一定正确的是( )
A. B. C. D.
3.下列图形中是中心对称图形但不是轴对称图形的是( )
A B C D
下图是由4个相同的正方体组成的立体图形,它的左视图是( )
如图,AC是⊙O直径,BC⊥AC于C, 连接AB交⊙O
于D,连接CD, AC=8,tan∠BCD=, 则AB长为( )
A. 8 B. 7 C. 10 D. 6
6.分式方程的解为( )
A. x=5 B. x=3 C. x=1 D. x=2
7.如图△ABC≌△DEC,点A和点D是对应顶点,当B和点E是对应顶点,
过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
A. 30° B. 25° C. 35° D. 65°
8.抛物线的顶点坐标为( )
A.(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
9.如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为( )
A. 3 B. 4 C. 5 D. 6
如图,△ABC中, AD、BE相交于点G,DF∥BE,下列结论错误的是( )
A. B. C. D.
二、填空题(每小题3分,共计30分)
11. 98 000米用科学记数法表示为 米.
12. 在函数y=中,自变量x的取值范围是 .
13.已知反比例函数y=的图象经过点(2,﹣9),则k的值为 .
14.计算 2 的结果是 .
15.把多项式分解因式的结果是 .
16.一个布袋里装有个红球,个白球,每个球除颜色外均相同,从中任意模出一个球,则摸出的球是红球的概率是__________.
17.不等式组的解集是 .
18. 某商品经过两次连续提价,每件售价由原来的100元上涨到了121元.
设平均每次涨价的百分率为x,则x是 .
19. 四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E,
若CE=2,则平行四边形ABCD的周长为 .
20. 如图,Rt△ABC中, ∠C=90°,AC=BC, 点D点、E分别在
BC、AB上, 连接AD、DE, ∠ADC=∠BDE, AD=2,
DE=, 则AE= .
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.(本题7分)
先化简,再求代数式的值,其中a =2sin45°﹣1.
22.(本题7分)
如图,方格中每个小正方形的边长为1个单位长度,△ABC的顶点和线段DE的端点均在小正方形的顶点上.
(1)在方格纸中将△ABC向上平移1个单位长度,再向右平移2个单位长度后得到△MNP(点A的对应点是M,点B的对应点是点N,点C的对应点是点P),请画出△MNP;
(2)在方格纸中画出以DE为斜边的等腰
直角三角形DEF(点F在小正方形的顶点上)
.连接FP,请直接写出线段FP的长.
23.(本题8分)
某中学开展以“我最喜欢的冰雪运动项目”为主题的调查活动,围绕冰球、冰壶、短道速滑、高山滑雪四种冰雪运动项目中,你最喜欢哪一种?(必选且只选一种)的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后回城如图所示的不完整的条形统计图,其中最喜欢短道速滑的学生人数占所调查人数的40%. 请你根据图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了
多少名学生?
(2)请通过计算补全条形统计图;
(3)若该中学共有1500名学生,
请你估计该中学最喜欢高山滑雪的
学生共有多少名?
24.(本题8分)
已知四边形ABCD是正方形,点E在边DA的延长线上,连接CE交AB于点G, B作BM⊥CE,垂足为点M。BM的延长线交AD于点F,交CD的延长线于点H.
(1)如图1,求证:CE=BH;
(2)如图2,若AE=AB,连接CF,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形(△AEG除外),使写出的每个三角形都与△AEG全等.
25.(本题10分)
某中学计划为书法小组购买某种品牌的A、B两种型号的毛笔.若购买3支A型号的毛笔和1支B型号的毛笔需用22元;若购买2支A型号的毛笔和3支B型号的毛笔需用24元.
(1)求每支A种型号的毛笔和每支B型号的毛笔各是多少元;
(2)该中学决定购买以上两种型号的毛笔共80支,总费用不超过420元,那么该中学最多可以购买多少支A种型号的毛笔?
26.(本题10分)
已知△ABC内接于⊙O,BD为⊙O的直径,连接AD,AC与BD交于点E.
(1)如图1,求证:∠ABD+∠ACB=90°;
(2)如图2,过点A作AG⊥BC,垂足为点G,AG交BD于点F,若EF=ED, 求证:AB=BC;
(3)如图3,在(2)的条件下,过点C作BD的平行线交AG的延长线与点H,交⊙O于点P,
连接BH,若∠BHP=45°,CH=6,求线段BH的长.
27.(本题10分)
如图,在平面直角坐标系中,直线AB的解析式为y=kx+3分别交x轴、y轴于点A、B,∠BAO=45°.
(1)求直线AB的解析式;
(2)点C在y轴负半轴上,连接CB,过点B作BC的垂线交x轴于点P,设点P的横坐标为t,△BAP的面积为S,求S与t之间的函数解析式,(不要求写出自变量t的取值范围) ;
(3)在(2)的条件下,延长BC至Q,使BQ=BP,过点Q作x轴的垂线交x轴于点D,点E为线段CQ的中点,过点E作BQ的垂线交BD的延长线与点F,若EF= , 求Q点坐标.
哈尔滨市第六十九中学学情自我监测
参考答案
选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C A C A B D B C
填空题:
11 12 13 14 15
9.8×104 x≠5 18 2 b(a+5)(a-5)
16 17 18 19 20
X< 10% 20或28 3
(1)略;(2)略;(3)
(1)y=-x+3;(2);(3)Q(-3,-6)
下面图形为参考图形
26.
27.
27.
同课章节目录
