2021-2022学年鲁教版(五四版)九年级数学下册5.2圆的对称性 同步辅导测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四版)九年级数学下册5.2圆的对称性 同步辅导测评(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 349.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 08:54:48 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学下册《5.2圆的对称性》优生辅导测评(附答案)
一.选择题(共11小题,满分44分)
1.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
2.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么所对的圆心角的大小是( )
A.60° B.75° C.80° D.90°
3.如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:
①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是( )
A.AB=AD B.BE=CD C.AC=BD D.BE=AD
5.如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
A.∠OBA=∠OCA B.四边形OABC内接于⊙O
C.AB=2BC D.∠OBA+∠BOC=90°
6.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
7.如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连接AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
A.50° B.65° C.100° D.130°
8.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
9.如图,MN是⊙O的直径,点A是半圆上一个三等分点,点B是的中点,点B'是点B关于MN的对称点,⊙O的半径为1,则AB'的长等于( )
A.1 B. C. D.2
10.如图,⊙O的直径CD的长为4,=,∠A=60°.则AC的长是( )
A.1 B. C.2 D.
11.如图,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,若∠AOC=54°,则∠E的度数为( )度.
A.27 B.24 C.20 D.18
二.填空题(共4小题,满分20分)
12.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
13.如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B= 度.
14.已知A、B、C是⊙O上的三点,若∠COA=120°,则∠CBA的度数为 .
15.已知半径为5的⊙O中,弦AB=5,弦AC=5,则∠BAC的度数是 .
三.解答题(共8小题,满分56分)
16.已知:如图,C,D是以AB为直径的⊙O上的两点,且OD∥BC.求证:AD=DC.
17.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
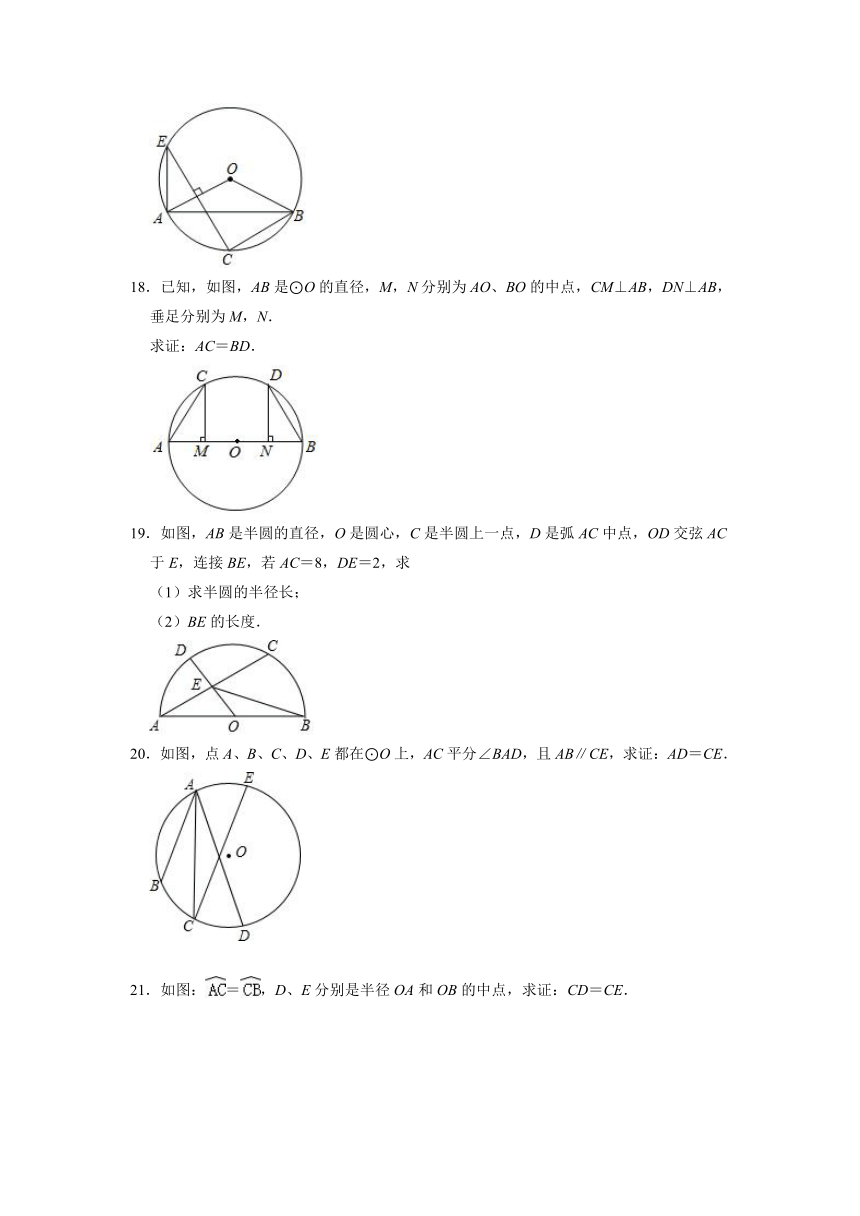
18.已知,如图,AB是⊙O的直径,M,N分别为AO、BO的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.
求证:AC=BD.
19.如图,AB是半圆的直径,O是圆心,C是半圆上一点,D是弧AC中点,OD交弦AC于E,连接BE,若AC=8,DE=2,求
(1)求半圆的半径长;
(2)BE的长度.
20.如图,点A、B、C、D、E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.
21.如图:=,D、E分别是半径OA和OB的中点,求证:CD=CE.
22.如图,⊙O中两条不平行弦AB和CD的中点M,N.且AB=CD,求证:∠AMN=∠CNM.
23.如图,⊙O中,弦AB=CD.求证:∠AOC=∠BOD.
参考答案
一.选择题(共11小题,满分44分)
1.解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=75°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
2.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中
,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即所对的圆心角的大小是90°,
故选:D.
3.解:如图连接OB、OD;
∵AB=CD,
∴=,故①正确
∵OM⊥AB,ON⊥CD,
∴AM=MB,CN=ND,
∴BM=DN,
∵OB=OD,
∴Rt△OMB≌Rt△OND,
∴OM=ON,故②正确,
∵OP=OP,
∴Rt△OPM≌Rt△OPN,
∴PM=PN,∠OPB=∠OPD,故④正确,
∵AM=CN,
∴PA=PC,故③正确,
故选:D.
4.解:
∵,
∴,
∴,
∴AC=BD,
故选:C.
5.解:过O作OD⊥AB于D交⊙O于E,
则=,
∴AE=BE,∠AOE=∠BOE=AOB,
∵∠AOB=2∠BOC,
∴∠AOE=∠BOE=∠BOC,
∴==,
∴AE=BE=BC,
∴2BC>AB,故C错误;
∵OA=OB=OC,
∴∠OBA=(180°﹣∠AOB)=90°﹣∠BOC,
∠OCA=(180°﹣∠AOC)=90°﹣∠BOC,
∴∠OBA≠∠OCA,故A错误;
∵点A,B,C在⊙O上,而点O在圆心,
∴四边形OABC不内接于⊙O,故B错误;
∵∠BOE=∠BOC=AOB,
∵∠BOE+∠OBA=90°,
∴∠OBA+∠BOC=90°,故D正确;
故选:D.
6.解:连接OC、OD,
∵BC=CD=DA,
∴∠COB=∠COD=∠DOA,
∵∠COB+∠COD+∠DOA=180°,
∴∠COB=∠COD=∠DOA=60°,
∴∠BCD=×2(180°﹣60°)=120°.
故选:C.
7.解:由题意可得:AB=AC,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠A=50°,
∴∠BOC=100°,
故选:C.
8.解:A、∵在一个圆中一条弦所对的弧有两条,∴等弦所对的弧不一定相等,故本选项错误;
B、相等的弧所对的弦一定相等,故本选项正确;
C、在同圆或等圆中,圆心角相等,所对的弦相等,故本选项错误;
D、在同圆或等圆中,弦相等所对的圆心角相等,故本选项错误.
故选:B.
9.解:连接OB、OB′,
∵点A是半圆上一个三等分点,
∴∠AON=60°,
∵点B是的中点,
∴∠BON=30°,
∵点B'是点B关于MN的对称点,
∴∠B′ON=30°,
∴∠AOB′=90°,
∴AB′==,
故选:B.
10.解:连接OA,过点O作OF⊥AC于F,
则AF=FC,
∵=,
∴AC=BC,
∵∠CAB=60°,
∴∠CBA=∠CAB=60°,
由圆周角定理得:∠AOC=2∠CBA=120°,
∵OA=OC,
∴∠OAC=30°,
∴AF=OA cos∠OAC=2×=,
∴AC=2AF=2,
故选:D.
11.解:连接OD,如图所示:
∵AB=2DE=2OD,
∴OD=DE,
∴∠DOE=∠E,
∵OC=OD,
∴∠OCD=∠ODC=∠DOE+∠E=2∠E,
设∠E=∠DOE=x,则∠OCD=∠ODC=2x,
∵∠AOC=∠C+∠E=2x+x=54°,
∴x=18°,即∠E=180°;
故选:D.
二.填空题(共4小题,满分20分)
12.解:连接OC,
∵AC∥DE,
∴∠A=∠1.∠2=∠ACO,
∵∠A=∠ACO,
∴∠1=∠2.
∴CE=BE=3.
13.解:如图,连接OA,
∵OA=OC,
∴∠OAC=∠C=20°,
∴∠OAB=60°,
∵OA=OB,
∴∠B=∠OAB=60°,
故答案为:60.
14.解:如图
当B点在优弧AC上,则∠ABC=∠AOC=60°;
当B点在劣弧AC上,即B′点,则∠B′+∠B=180°,
所以∠B′=120°.
故答案为:60°或120°.
15.解:如图,连接OC,OA,OB.
∵OC=OA=AC=5,
∴△OAC是等边三角形,
∴∠CAO=60°,
∵OA=OB=5,AB=5,
∴OA2+OB2=50=AB2,
∴△OAB是等腰直角三角形,∠OAB=45°,
点C的位置有两种情况,如左图时,∠BAC=∠CAO+∠OAB=60°+45°=105°;
如右图时,∠BAC=∠CAO﹣∠OAB=60°﹣45°=15°.
综上所述:∠BAC=15°或105°.
三.解答题(共8小题,满分56分)
16.证明:连接OC,如图,
∵OD∥BC,
∴∠1=∠B,∠2=∠3,
又∵OB=OC,
∴∠B=∠3,
∴∠1=∠2,
∴AD=DC.
17.证明:连OC,AC,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴=,
∴AE=AC,
∴AE=AO.
18.证明:连接OC、OD,
∵AB是⊙O的直径,
∴AO=BO,
∵M,N分别为AO、BO的中点,
∴OM=ON,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴△OCM与△ODN都是直角三角形,
又∵OC=OD,
∴△OCM≌△ODN(HL),
∴∠AOC=∠BOD,
∴AC=BD.
19.解:(1)设圆的半径为r,
∵D是弧AC中点,
∴OD⊥AC,AE=AC=4,
在Rt△AOE中,OA2=OE2+AE2,即r2=(r﹣2)2+42,
解得,r=5,即圆的半径长为5;
(2)连接BC,
∵AO=OB,AE=EC,
∴BC=2OE=6,
∵AB是半圆的直径,
∴∠ACB=90°,
∴BE==2.
20.证明:如图,∵AB∥CE,
∴∠ACE=∠BAC.
又∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴∠C=∠CAD,
∴=,
∴+=+,
∴=,
∴AD=CE.
21.证明:连接OC.
在⊙O中,∵=
∴∠AOC=∠BOC,
∵OA=OB,D、E分别是半径OA和OB的中点,
∴OD=OE,
∵OC=OC(公共边),
∴△COD≌△COE(SAS),
∴CD=CE(全等三角形的对应边相等).
22.证明:连OM,ON,如图,
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,
∴∠AMO=∠CNO=90°,
∵AB=CD,
∴OM=ON,
∴∠OMN=∠ONM,
∴∠AMN=∠CNM.
23.解:∵弦AB=CD(已知),
∴=;
∴∠AOB=∠COD,
∴∠AOB﹣∠BOC=∠COD﹣∠BOC,
即∠AOC=∠BOD.
一.选择题(共11小题,满分44分)
1.如图,圆O通过五边形OABCD的四个顶点.若=150°,∠A=75°,∠D=60°,则的度数为何?( )
A.25° B.40° C.50° D.60°
2.如图,在5×5正方形网格中,一条圆弧经过A、B、C三点,那么所对的圆心角的大小是( )
A.60° B.75° C.80° D.90°
3.如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:
①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是( )
A.AB=AD B.BE=CD C.AC=BD D.BE=AD
5.如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
A.∠OBA=∠OCA B.四边形OABC内接于⊙O
C.AB=2BC D.∠OBA+∠BOC=90°
6.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
7.如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连接AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
A.50° B.65° C.100° D.130°
8.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
9.如图,MN是⊙O的直径,点A是半圆上一个三等分点,点B是的中点,点B'是点B关于MN的对称点,⊙O的半径为1,则AB'的长等于( )
A.1 B. C. D.2
10.如图,⊙O的直径CD的长为4,=,∠A=60°.则AC的长是( )
A.1 B. C.2 D.
11.如图,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,若∠AOC=54°,则∠E的度数为( )度.
A.27 B.24 C.20 D.18
二.填空题(共4小题,满分20分)
12.如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE= .
13.如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B= 度.
14.已知A、B、C是⊙O上的三点,若∠COA=120°,则∠CBA的度数为 .
15.已知半径为5的⊙O中,弦AB=5,弦AC=5,则∠BAC的度数是 .
三.解答题(共8小题,满分56分)
16.已知:如图,C,D是以AB为直径的⊙O上的两点,且OD∥BC.求证:AD=DC.
17.如图,A、B是⊙O上的两点,∠AOB=120°,C是弧AB的中点,CE⊥OA交⊙O于点E,连接AE.求证:AE=AO.
18.已知,如图,AB是⊙O的直径,M,N分别为AO、BO的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.
求证:AC=BD.
19.如图,AB是半圆的直径,O是圆心,C是半圆上一点,D是弧AC中点,OD交弦AC于E,连接BE,若AC=8,DE=2,求
(1)求半圆的半径长;
(2)BE的长度.
20.如图,点A、B、C、D、E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.
21.如图:=,D、E分别是半径OA和OB的中点,求证:CD=CE.
22.如图,⊙O中两条不平行弦AB和CD的中点M,N.且AB=CD,求证:∠AMN=∠CNM.
23.如图,⊙O中,弦AB=CD.求证:∠AOC=∠BOD.
参考答案
一.选择题(共11小题,满分44分)
1.解:连接OB、OC,
∵OA=OB=OC=OD,
∴△OAB、△OBC、△OCD,皆为等腰三角形,
∵∠A=75°,∠D=60°,
∴∠1=180°﹣2∠A=180°﹣2×75°=30°,∠2=180°﹣2∠D=180°﹣2×60°=60°,
∵=150°,
∴∠AOD=150°,
∴∠3=∠AOD﹣∠1﹣∠2=150°﹣30°﹣60°=60°,
则的度数为60°.
故选:D.
2.解:作AB的垂直平分线,作BC的垂直平分线,如图,
它们都经过Q,所以点Q为这条圆弧所在圆的圆心.
连接AQ,CQ,
在△APQ与△CQN中
,
∴△APQ≌△CQN(SAS),
∴∠AQP=∠CQN,∠PAQ=∠CQN
∵∠AQP+∠PAQ=90°,
∴∠AQP+∠CQN=90°,
∴∠AQC=90°,
即所对的圆心角的大小是90°,
故选:D.
3.解:如图连接OB、OD;
∵AB=CD,
∴=,故①正确
∵OM⊥AB,ON⊥CD,
∴AM=MB,CN=ND,
∴BM=DN,
∵OB=OD,
∴Rt△OMB≌Rt△OND,
∴OM=ON,故②正确,
∵OP=OP,
∴Rt△OPM≌Rt△OPN,
∴PM=PN,∠OPB=∠OPD,故④正确,
∵AM=CN,
∴PA=PC,故③正确,
故选:D.
4.解:
∵,
∴,
∴,
∴AC=BD,
故选:C.
5.解:过O作OD⊥AB于D交⊙O于E,
则=,
∴AE=BE,∠AOE=∠BOE=AOB,
∵∠AOB=2∠BOC,
∴∠AOE=∠BOE=∠BOC,
∴==,
∴AE=BE=BC,
∴2BC>AB,故C错误;
∵OA=OB=OC,
∴∠OBA=(180°﹣∠AOB)=90°﹣∠BOC,
∠OCA=(180°﹣∠AOC)=90°﹣∠BOC,
∴∠OBA≠∠OCA,故A错误;
∵点A,B,C在⊙O上,而点O在圆心,
∴四边形OABC不内接于⊙O,故B错误;
∵∠BOE=∠BOC=AOB,
∵∠BOE+∠OBA=90°,
∴∠OBA+∠BOC=90°,故D正确;
故选:D.
6.解:连接OC、OD,
∵BC=CD=DA,
∴∠COB=∠COD=∠DOA,
∵∠COB+∠COD+∠DOA=180°,
∴∠COB=∠COD=∠DOA=60°,
∴∠BCD=×2(180°﹣60°)=120°.
故选:C.
7.解:由题意可得:AB=AC,
∵∠ABC=65°,
∴∠ACB=65°,
∴∠A=50°,
∴∠BOC=100°,
故选:C.
8.解:A、∵在一个圆中一条弦所对的弧有两条,∴等弦所对的弧不一定相等,故本选项错误;
B、相等的弧所对的弦一定相等,故本选项正确;
C、在同圆或等圆中,圆心角相等,所对的弦相等,故本选项错误;
D、在同圆或等圆中,弦相等所对的圆心角相等,故本选项错误.
故选:B.
9.解:连接OB、OB′,
∵点A是半圆上一个三等分点,
∴∠AON=60°,
∵点B是的中点,
∴∠BON=30°,
∵点B'是点B关于MN的对称点,
∴∠B′ON=30°,
∴∠AOB′=90°,
∴AB′==,
故选:B.
10.解:连接OA,过点O作OF⊥AC于F,
则AF=FC,
∵=,
∴AC=BC,
∵∠CAB=60°,
∴∠CBA=∠CAB=60°,
由圆周角定理得:∠AOC=2∠CBA=120°,
∵OA=OC,
∴∠OAC=30°,
∴AF=OA cos∠OAC=2×=,
∴AC=2AF=2,
故选:D.
11.解:连接OD,如图所示:
∵AB=2DE=2OD,
∴OD=DE,
∴∠DOE=∠E,
∵OC=OD,
∴∠OCD=∠ODC=∠DOE+∠E=2∠E,
设∠E=∠DOE=x,则∠OCD=∠ODC=2x,
∵∠AOC=∠C+∠E=2x+x=54°,
∴x=18°,即∠E=180°;
故选:D.
二.填空题(共4小题,满分20分)
12.解:连接OC,
∵AC∥DE,
∴∠A=∠1.∠2=∠ACO,
∵∠A=∠ACO,
∴∠1=∠2.
∴CE=BE=3.
13.解:如图,连接OA,
∵OA=OC,
∴∠OAC=∠C=20°,
∴∠OAB=60°,
∵OA=OB,
∴∠B=∠OAB=60°,
故答案为:60.
14.解:如图
当B点在优弧AC上,则∠ABC=∠AOC=60°;
当B点在劣弧AC上,即B′点,则∠B′+∠B=180°,
所以∠B′=120°.
故答案为:60°或120°.
15.解:如图,连接OC,OA,OB.
∵OC=OA=AC=5,
∴△OAC是等边三角形,
∴∠CAO=60°,
∵OA=OB=5,AB=5,
∴OA2+OB2=50=AB2,
∴△OAB是等腰直角三角形,∠OAB=45°,
点C的位置有两种情况,如左图时,∠BAC=∠CAO+∠OAB=60°+45°=105°;
如右图时,∠BAC=∠CAO﹣∠OAB=60°﹣45°=15°.
综上所述:∠BAC=15°或105°.
三.解答题(共8小题,满分56分)
16.证明:连接OC,如图,
∵OD∥BC,
∴∠1=∠B,∠2=∠3,
又∵OB=OC,
∴∠B=∠3,
∴∠1=∠2,
∴AD=DC.
17.证明:连OC,AC,如图,
∵∠AOB=120°,C是弧AB的中点,
∴∠AOC=60°,
∵OA=OC,
∴△AOC为等边三角形,
∴AC=AO,
∵OA⊥CE,
∴=,
∴AE=AC,
∴AE=AO.
18.证明:连接OC、OD,
∵AB是⊙O的直径,
∴AO=BO,
∵M,N分别为AO、BO的中点,
∴OM=ON,
∵CM⊥AB,DN⊥AB,
∴∠CMO=∠DNO=90°,
∴△OCM与△ODN都是直角三角形,
又∵OC=OD,
∴△OCM≌△ODN(HL),
∴∠AOC=∠BOD,
∴AC=BD.
19.解:(1)设圆的半径为r,
∵D是弧AC中点,
∴OD⊥AC,AE=AC=4,
在Rt△AOE中,OA2=OE2+AE2,即r2=(r﹣2)2+42,
解得,r=5,即圆的半径长为5;
(2)连接BC,
∵AO=OB,AE=EC,
∴BC=2OE=6,
∵AB是半圆的直径,
∴∠ACB=90°,
∴BE==2.
20.证明:如图,∵AB∥CE,
∴∠ACE=∠BAC.
又∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴∠C=∠CAD,
∴=,
∴+=+,
∴=,
∴AD=CE.
21.证明:连接OC.
在⊙O中,∵=
∴∠AOC=∠BOC,
∵OA=OB,D、E分别是半径OA和OB的中点,
∴OD=OE,
∵OC=OC(公共边),
∴△COD≌△COE(SAS),
∴CD=CE(全等三角形的对应边相等).
22.证明:连OM,ON,如图,
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,
∴∠AMO=∠CNO=90°,
∵AB=CD,
∴OM=ON,
∴∠OMN=∠ONM,
∴∠AMN=∠CNM.
23.解:∵弦AB=CD(已知),
∴=;
∴∠AOB=∠COD,
∴∠AOB﹣∠BOC=∠COD﹣∠BOC,
即∠AOC=∠BOD.
