2021-2022学年人教版八年级上册数学14.2 乘法公式 练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级上册数学14.2 乘法公式 练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 376.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 09:00:26 | ||
图片预览


文档简介
14.2 乘法公式
一、选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
1.下列算式中不能利用平方差公式计算的是( )
A. B.
C. D.
2.若,且,则等于( ).
A.7 B.6 C.5 D.8
3.已知a+b+3=0,且a﹣b﹣4=0,则a2﹣b2=( )
A.12 B.﹣12 C.24 D.±12
4.若,,则( )
A.1 B.-1 C.3 D.-3
5.三个连续的偶数,若中间一个为,则它们的积是( )
A. B. C. D.
6.如果y2+my+9是完全平方式,则m=( )
A.6 B.3 C.3或-3 D.6或-6
7.已知,,则的值为( )
A. B. C. D.
8.已知,且,则等于( ).
A.3 B.5 C.-3 D.1
9.下列四个整式:①x2﹣4x+4;②6x2+3x+1;③4x2+4x+1;④x2+4xy+2y2.其中是完全平方式的是( )
A.①③ B.①②③ C.②③④ D.③④
10.我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形揭示了(为非负整数)展开式的项数及各项系数的有关规律,根据“杨辉三角”请计算的展开式中从左起第四项的系数为( )
A. B. C. D.
二、填空题(每题3分,共15分)
11.设的小数部分为,则____________.
12.观察下列各式:
(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;……
根据这一规律计算:22020+22019+22018+…+22+2+1的结果是___________________.
13.如图是三种不同类型的地砖,若现有A类9块,B类5块,C类1块,若要拼成一个正方形还需B类地砖_____块.
14.若a=x+20,b=x+19,c=x+21,则a2+b2+c2-ab-bc-ac=___________.
15.已知实数满足,则的值是______.
三、解答题(共55分)
16.(4分)计算:
17.(5分)化简:(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b).
18.(7分)先化简,再求值:,其中,.
19.(7分)先化简,再求值:,其中,.
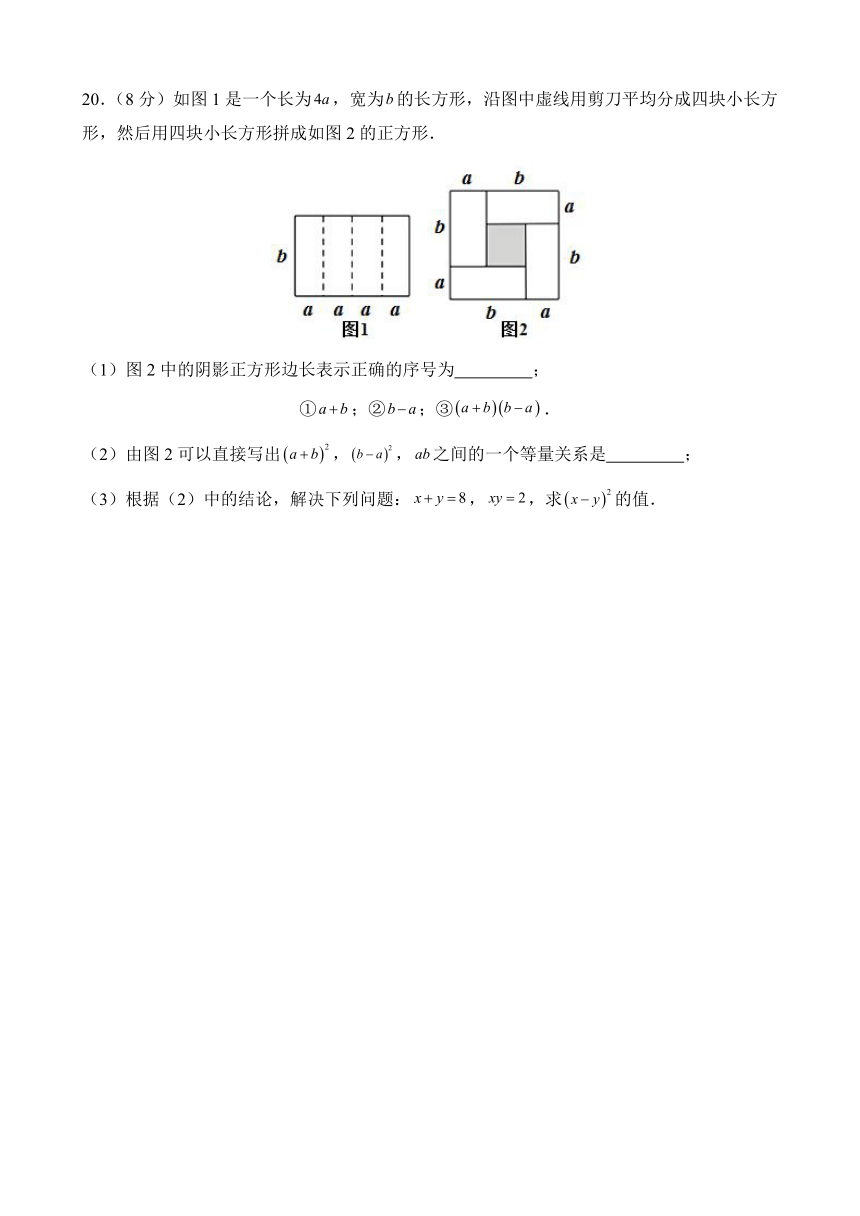
20.(8分)如图1是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形.
(1)图2中的阴影正方形边长表示正确的序号为 ;
①;②;③.
(2)由图2可以直接写出,,之间的一个等量关系是 ;
(3)根据(2)中的结论,解决下列问题:,,求的值.
21.(9分)给出下列算式:;
;
;
.
······
观察上面一系列式子,你能发现什么规律
用含为正整数)的式子表示出来你发现的规律,并证明这个规律﹔
计算_ _,此时_ .
22.(9分)老师在讲完乘法公式的多种运用后,要求同学们运用所学知识解答:求代数式的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:
∵,
当时,的值最小,最小值是0,
∴
当时,的值最小,最小值是1,
∴的最小值是1.
请你根据上述方法,解答下列各题
(1)当x=______时,代数式的最小值是______;
(2)若,当x=______时,y有最______值(填“大”或“小”),这个值是______;
(3)若,求的最小值.
【参考答案】
一、选择题(每题3分,共30分)
1—5 CBBDB 6—10 DBBAC
二、填空题(每空3分,共15分)
11. 4 12.22021-1 13. 1 14. 3 15. 7
三、解答题(共55分)
16.
17.解:
.
18.解:原式
,
当,时,原式.
19.解:
当,时
原式
20.(1)②.
(2).
(3)解:由(2)的结论可得,
把,代入得,,
所以.
21.(1)规律:两个连续奇数的平方差(大奇数的平方减去小奇数的平方),等于夹在两个奇数之间的偶数的倍;
(2)设表示自然数,用关于的等式表示这个规律为:
;
证明:左边右边
;
(3),
解得:,
.
22.(1)∵,
∴当时,有最小值3;
故答案为3,3.
(2)∵,
∴当时最大值-2;
故答案为1,大,-2.
(3)∵,
∴
∴,
∵,
∴,
∴当时,的最小值为-6.
一、选择题(下列各题的四个选项中,只有一项符合题目要求。每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案
1.下列算式中不能利用平方差公式计算的是( )
A. B.
C. D.
2.若,且,则等于( ).
A.7 B.6 C.5 D.8
3.已知a+b+3=0,且a﹣b﹣4=0,则a2﹣b2=( )
A.12 B.﹣12 C.24 D.±12
4.若,,则( )
A.1 B.-1 C.3 D.-3
5.三个连续的偶数,若中间一个为,则它们的积是( )
A. B. C. D.
6.如果y2+my+9是完全平方式,则m=( )
A.6 B.3 C.3或-3 D.6或-6
7.已知,,则的值为( )
A. B. C. D.
8.已知,且,则等于( ).
A.3 B.5 C.-3 D.1
9.下列四个整式:①x2﹣4x+4;②6x2+3x+1;③4x2+4x+1;④x2+4xy+2y2.其中是完全平方式的是( )
A.①③ B.①②③ C.②③④ D.③④
10.我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形揭示了(为非负整数)展开式的项数及各项系数的有关规律,根据“杨辉三角”请计算的展开式中从左起第四项的系数为( )
A. B. C. D.
二、填空题(每题3分,共15分)
11.设的小数部分为,则____________.
12.观察下列各式:
(x﹣1)(x+1)=x2﹣1;
(x﹣1)(x2+x+1)=x3﹣1;
(x﹣1)(x3+x2+x+1)=x4﹣1;……
根据这一规律计算:22020+22019+22018+…+22+2+1的结果是___________________.
13.如图是三种不同类型的地砖,若现有A类9块,B类5块,C类1块,若要拼成一个正方形还需B类地砖_____块.
14.若a=x+20,b=x+19,c=x+21,则a2+b2+c2-ab-bc-ac=___________.
15.已知实数满足,则的值是______.
三、解答题(共55分)
16.(4分)计算:
17.(5分)化简:(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b).
18.(7分)先化简,再求值:,其中,.
19.(7分)先化简,再求值:,其中,.
20.(8分)如图1是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成如图2的正方形.
(1)图2中的阴影正方形边长表示正确的序号为 ;
①;②;③.
(2)由图2可以直接写出,,之间的一个等量关系是 ;
(3)根据(2)中的结论,解决下列问题:,,求的值.
21.(9分)给出下列算式:;
;
;
.
······
观察上面一系列式子,你能发现什么规律
用含为正整数)的式子表示出来你发现的规律,并证明这个规律﹔
计算_ _,此时_ .
22.(9分)老师在讲完乘法公式的多种运用后,要求同学们运用所学知识解答:求代数式的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:
∵,
当时,的值最小,最小值是0,
∴
当时,的值最小,最小值是1,
∴的最小值是1.
请你根据上述方法,解答下列各题
(1)当x=______时,代数式的最小值是______;
(2)若,当x=______时,y有最______值(填“大”或“小”),这个值是______;
(3)若,求的最小值.
【参考答案】
一、选择题(每题3分,共30分)
1—5 CBBDB 6—10 DBBAC
二、填空题(每空3分,共15分)
11. 4 12.22021-1 13. 1 14. 3 15. 7
三、解答题(共55分)
16.
17.解:
.
18.解:原式
,
当,时,原式.
19.解:
当,时
原式
20.(1)②.
(2).
(3)解:由(2)的结论可得,
把,代入得,,
所以.
21.(1)规律:两个连续奇数的平方差(大奇数的平方减去小奇数的平方),等于夹在两个奇数之间的偶数的倍;
(2)设表示自然数,用关于的等式表示这个规律为:
;
证明:左边右边
;
(3),
解得:,
.
22.(1)∵,
∴当时,有最小值3;
故答案为3,3.
(2)∵,
∴当时最大值-2;
故答案为1,大,-2.
(3)∵,
∴
∴,
∵,
∴,
∴当时,的最小值为-6.
