2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 362.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 09:11:45 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》同步达标测评(附答案)
一.选择题(共8小题,满分40分)
1.已知△ABC和△DEF中,∠B=∠E=100°,下列条件不能得到两个三角形相似的是( )
A.∠A=∠D B.=
C.∠C=∠D D.∠C=40°,∠D=30°
2.如图,在△ABC中,∠B=80°,∠C=40°,直线l平行于BC.现将直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,若△AMN与△ABC相似,则旋转角为( )
A.20° B.40° C.60° D.80°
3.若如图所示的两个四边形相似,则∠α的度数是( )
A.80° B.60° C.70° D.150°
4.如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,且AP=2.8,过点P沿直线剪下一个与△ABC相似的小三角形纸板,则不同的剪法有( )
A.2种 B.3种 C.4种 D.5种
5.如图,△ABC中,DE∥BC,=,△ADE的面积是2,那么△BEC的面积是( )
A.6 B.8 C.12 D.18
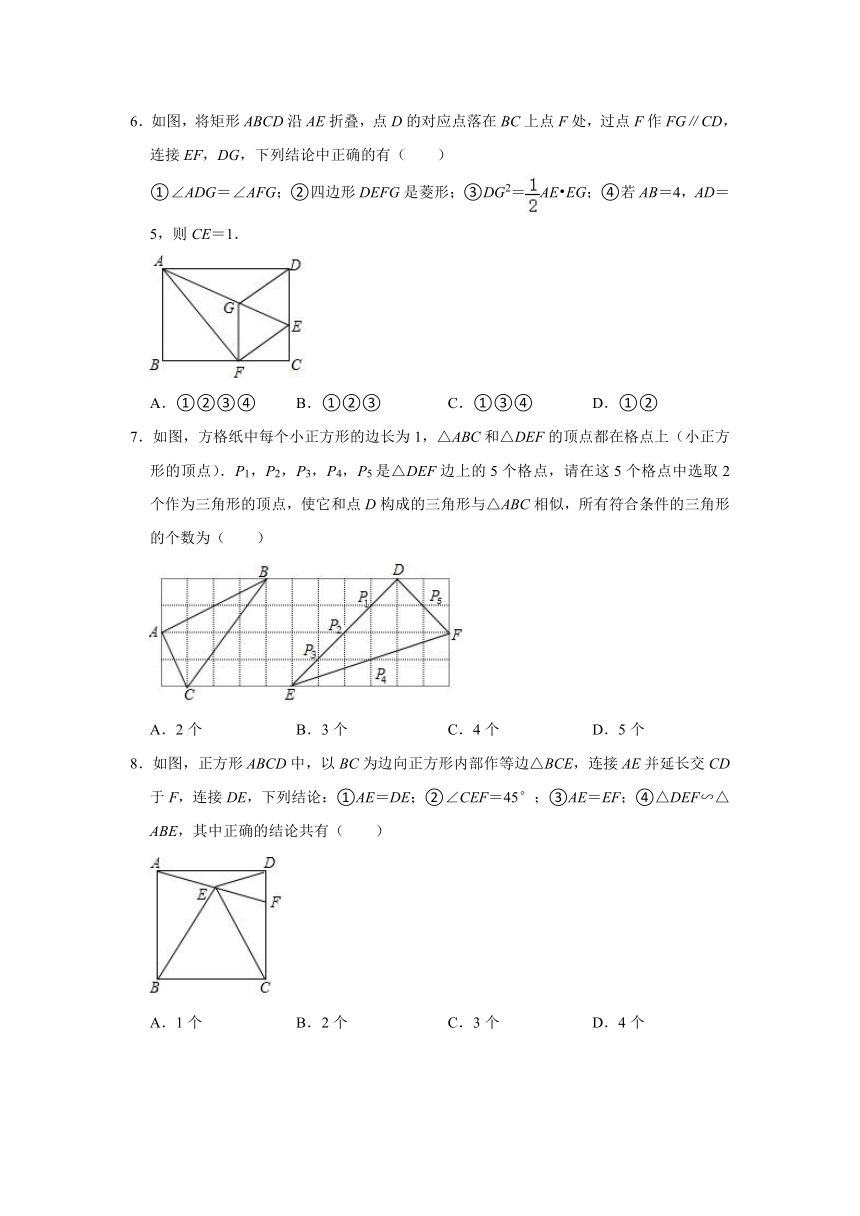
6.如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=AE EG;④若AB=4,AD=5,则CE=1.
A.①②③④ B.①②③ C.①③④ D.①②
7.如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在格点上(小正方形的顶点).P1,P2,P3,P4,P5是△DEF边上的5个格点,请在这5个格点中选取2个作为三角形的顶点,使它和点D构成的三角形与△ABC相似,所有符合条件的三角形的个数为( )
A.2个 B.3个 C.4个 D.5个
8.如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE,连接AE并延长交CD于F,连接DE,下列结论:①AE=DE;②∠CEF=45°;③AE=EF;④△DEF∽△ABE,其中正确的结论共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,满分40分)
9.如图,在△ABC中,D,E分别是AB,AC上的点(DE≠BC),使△ADE∽△ACB的一个条件可以是 .
10.如图,矩形ABCD∽BCFE,且AE=3,AD=2,则BE的长为 .
11.等边三角形ABC和△A′B′C′相似,相似比为5:2,若AB=10,B′C′边上的高是 .
12.如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1,S2,S3,S4,以下判断:
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4,
④若△PAB∽△PDA,则PA=2
其中正确的是 (把所有正确的结论的序号都填在横线上).
13.如图,在 ABCD中,E为AD的三等分点,AE=AD,连接BE,交AC于点F,AC=15,则AF为 .
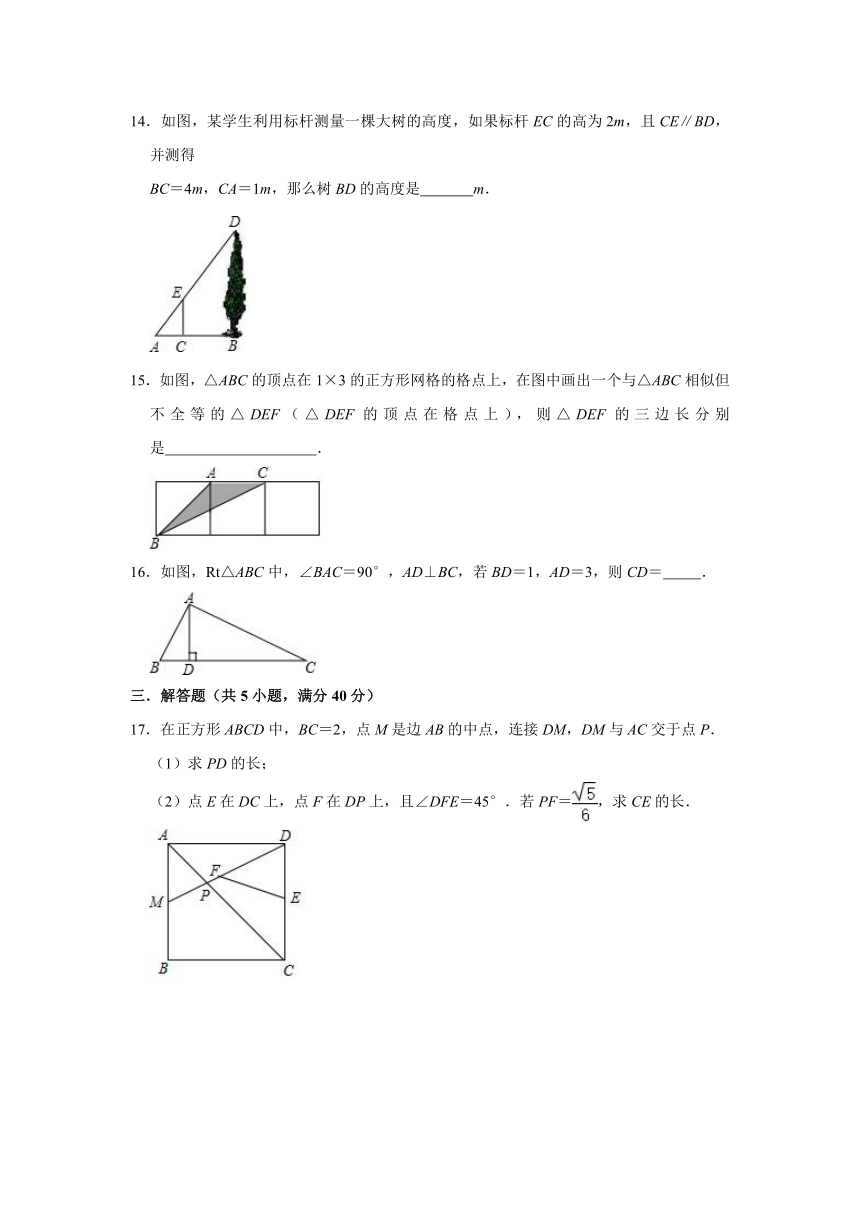
14.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,且CE∥BD,并测得
BC=4m,CA=1m,那么树BD的高度是 m.
15.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
16.如图,Rt△ABC中,∠BAC=90°,AD⊥BC,若BD=1,AD=3,则CD= .
三.解答题(共5小题,满分40分)
17.在正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P.
(1)求PD的长;
(2)点E在DC上,点F在DP上,且∠DFE=45°.若PF=,求CE的长.
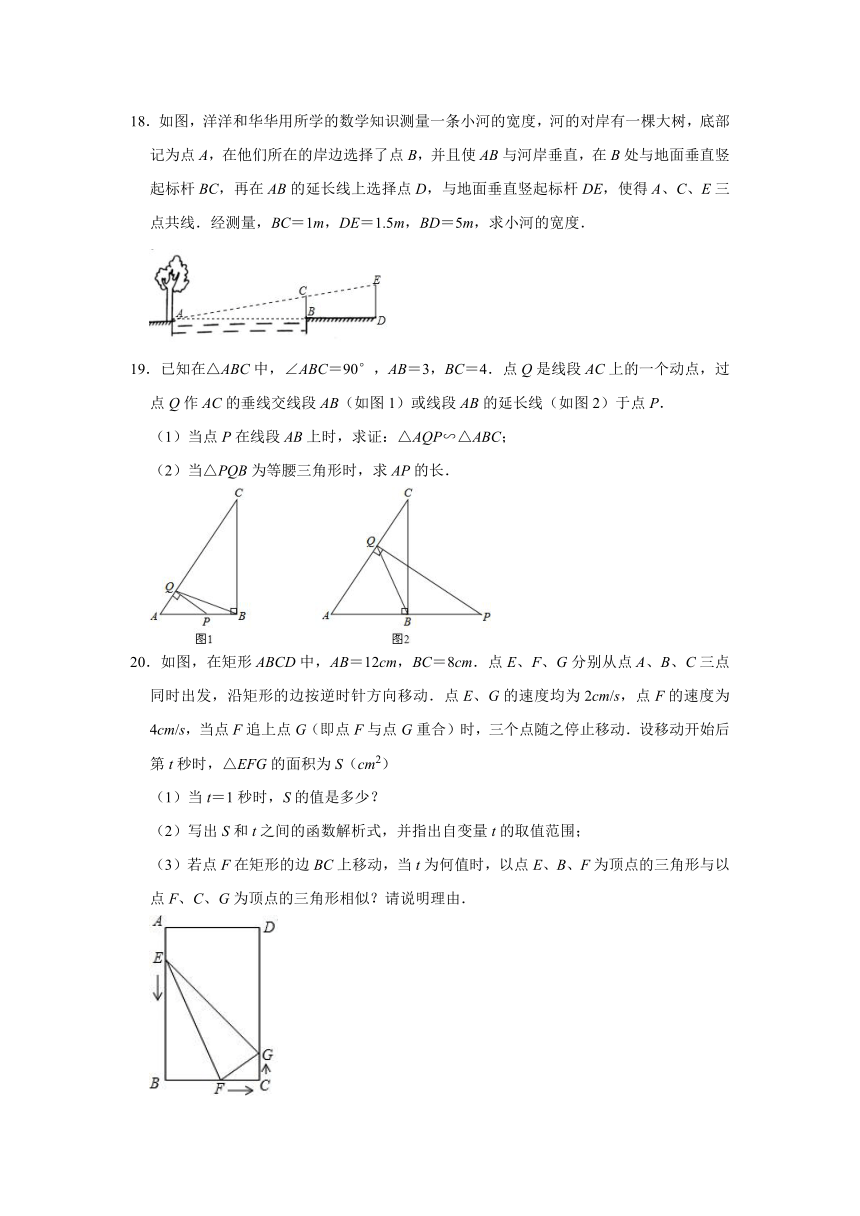
18.如图,洋洋和华华用所学的数学知识测量一条小河的宽度,河的对岸有一棵大树,底部记为点A,在他们所在的岸边选择了点B,并且使AB与河岸垂直,在B处与地面垂直竖起标杆BC,再在AB的延长线上选择点D,与地面垂直竖起标杆DE,使得A、C、E三点共线.经测量,BC=1m,DE=1.5m,BD=5m,求小河的宽度.
19.已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
20.如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动.点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2)
(1)当t=1秒时,S的值是多少?
(2)写出S和t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点E、B、F为顶点的三角形与以点F、C、G为顶点的三角形相似?请说明理由.
21.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
参考答案
一.选择题(共8小题,满分40分)
1.解:在△ABC和△DEF中,∠B=∠E=100°,
A、当∠A=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
B、当时,△ABC∽△DEF,故能判定这两个三角形相似;
C、当∠C=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
D、当∠C=40°,∠D=30°时,不能判断这两个三角形相似.
故选:D.
2.解:如图,直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,
若△AMN∽△ACB,则∠AMN=∠C=40°,
又∵直线l平行于BC,
∴∠ADE=∠B=80°,
∴∠DFM=∠ADE﹣∠AMN=80°﹣40°=40°,
即直线l旋转前后的夹角为40°,
∴旋转角为40°,
故选:B.
3.解:如图,
∵四边形ABCD∽四边形A′B′C′D′,
∴∠A=∠A′=150°,
∵∠B′=∠B=60°,∠C′=∠C=80°,
∴∠α=360°﹣∠A′﹣∠B′﹣∠C′=70°.
故选:C.
4.解:如图所示,过P作PD∥AB交BC于D或PE∥BC交AB于E,则△PCD∽△ACB或△APE∽△ACB,
如图所示,过P作∠APF=∠B交AB于F,则△APF∽△ABC,
故选:B.
5.解:∵△ABC中,DE∥BC,=,△ADE的面积是2,
∴△BDE的面积是4,
∴△ADE∽△ABC,
∴,
∴△ABC的面积=18,
∴△BEC的面积=18﹣2﹣4=12,
故选:C.
6.解:①由折叠可得,AD=AF,DG=FG,
在△ADG和△AFG中,
,
∴△ADG≌△AFG(SSS),
∴∠ADG=∠AFG,故①正确;
②∵GF∥DC,
∴∠EGF=∠DEG,
由翻折的性质可知:GD=GF,DE=EF,∠DGE=∠EGF,
∴∠DGE=∠DEG,
∴GD=DE,
∴DG=GF=DE=EF,
∴四边形DEFG为菱形,故②正确;
③如图所示,连接DF交AE于O,
∵四边形DEFG为菱形,
∴GE⊥DF,OG=OE=GE,
∵∠DOE=∠ADE=90°,∠OED=∠DEA,
∴△DOE∽△ADE,
∴=,即DE2=EO AE,
∵EO=GE,DE=DG,
∴DG2=AE EG,故③正确;
④由折叠可得,AF=AD=5,
∴Rt△ABF中,BF==3,
∴CF=5﹣3=2,
设CE=x,则DE=EF=4﹣x,
∵Rt△CEF中,CE2+CF2=EF2,
∴x2+22=(4﹣x)2,
解得x=,
∴CE=,故④错误;
故选:B.
7.解:设网格的边长为1.
则AC=,AB=,BC=.
连接P2P5,
DP5=,DP2=,P2P5=.
∵,
∴△ACB∽△DP5P2.
同理可找到△DP2P4,△DP4P5和△ACB相似.
故选:B.
8.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠ADC=90°,
∵△EBC是等边三角形,
∴BC=BE=CE,∠EBC=∠EBC=∠ECB=60°,
∴∠ABE=∠ECF=30°,
∵BA=BE,EC=CD,
∴∠BAE=∠BEA=∠CED=∠CDE=(180°﹣30°)=75°,
∴∠EAD=∠EDA=15°,
∴EA=ED,故①正确,
∴∠DEF=∠EAD+∠ADE=30°,
∴∠CEF=∠CED﹣∠DEF=45°,故②正确,
∵∠EDF=∠AFD=75°,
∴ED=EF,
∴AE=EF,故③正确,
∵∠BAE=∠BEA=∠EDF=∠EFD=75°,
∴△DEF∽△ABE,故④正确,
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵∠A=∠A
∴当∠ADE=∠C或∠AED=∠B或= 时,△ADE∽△ABC,
故答案为:∠ADE=∠C或∠AED=∠B或=.
10.解:∵四边形ABCD和四边形BCFE是矩形,
∴BC=EF=AD=2,
∵矩形ABCD∽BCFE,
∴=,
∴=,
∴BE=1(负值舍去),
故答案为:1.
11.解:∵△ABC是等边三角形,且AB=10,
∴BC边上的高为5,
∵△ABC∽△A′B′C′,且相似比为5:2,
∴B′C′边上的高是2.
12.解:①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB∽△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°﹣(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④错误.
故答案为①②③.
13.解:在 ABCD中,AD=BC,AD∥BC,
∵E为AD的三等分点,
∴AE=AD=BC,
∵AD∥BC,
∴==,
∵AC=15,
∴AF=×15=6.
故答案为6.
14.解:∵EC∥AB,BD⊥AB,
∴EC∥BD,∠ACE=∠ABD=90°,
在Rt△ACE∽Rt△ABD中,∠A=∠A,∠ACE=∠ABD=90°,
∴Rt△ACE∽Rt△ABD,
∴,即,解得BD=10m.
故答案为:10
15.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
16.解:∵Rt△ABC中,∠BAC=90°,
∴∠B+∠C=90°.
∵AD⊥BC于点D,
∴∠B+∠BAD=90°,∠C+∠CAD=90°,
∴∠BAD=∠C,∠B=∠CAD,
∴△ABD∽△CAD,
∴AD2=BD CD,
∵BD=1,AD=3,
∴CD=9,
故答案为:9
三.解答题(共5小题,满分40分)
17.解:(1)如图作PK⊥AD于K,PH⊥AB于H.
∵四边形ABCD是正方形,
∴∠PAD=∠PAB=45°,
∵PK⊥AD,PH⊥AB,
∴PK=PH,
∴===,
∴AB=AD=2,AM=BM=1,
∴DM=,
∴=2,
∴PD=×=.
(2)∵PF=,PD=,DM=,
∴DF=,PM=,
∵DE∥AM,
∴∠AMP=∠EDF,
∵∠DFE=∠MAP=45°,
∴△AMP∽△FDE,
∴=,
∴=,
∴DE=,
∴EC=2﹣=.
18.解:设小河的宽度AB=xm,根据题意得:BC⊥AD,ED⊥AD,
∴△ABC∽△ADE,
∴AB:AD=BC:ED,
∴x:(x+5)=1:1.5,
解得x=10,∴AB=10,
即小河的宽度为10米.
19.(1)证明:∵PQ⊥AQ,
∴∠AQP=90°=∠ABC,
在△APQ与△ABC中,
∵∠AQP=90°=∠ABC,∠A=∠A,
∴△AQP∽△ABC.
(2)解:在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,
(I)当点P在线段AB上时,如题图1所示.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ,
由(1)可知,△AQP∽△ABC,
∴,即,解得:PB=,
∴AP=AB﹣PB=3﹣=;
(II)当点P在线段AB的延长线上时,如题图2所示.
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是PB=BQ.
∵BP=BQ,∴∠BQP=∠P,
∵∠BQP+∠AQB=90°,∠A+∠P=90°,
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AP中点,
∴AP=2AB=2×3=6.
综上所述,当△PQB为等腰三角形时,AP的长为或6.
20.解:(1)如图1,当t=1秒时,AE=2,EB=10,BF=4,FC=4,CG=2,
由S=S梯形GCBE﹣S△EBF﹣S△FCG,
=×﹣
=×(10+2)×8﹣×10×4﹣
=24(cm2);
(2)①如图1,当0≤t≤2时,点E、F、G分别在边AB、BC、CD上移动,
此时AE=2t,EB=12﹣2t,BF=4t,FC=8﹣4t,CG=2t,
S=S梯形GCBE﹣S△EBF﹣S△FCG
=×(EB+CG) BC﹣EB BF﹣FC CG
=×8×(12﹣2t+2t)﹣×4t(12﹣2t)﹣×2t(8﹣4t)
=8t2﹣32t+48(0≤t≤2).
②如图2,当点F追上点G时,4t=2t+8,解得t=4,
当2<t<4时,点E在边AB上移动,点F、G都在边CD上移动,此时CF=4t﹣8,CG=2t,
FG=CG﹣CF=2t﹣(4t﹣8)=8﹣2t,
S=FG BC=(8﹣2t) 8=﹣8t+32.
即S=﹣8t+32(2<t<4).
(3)如图1,当点F在矩形的边BC上的边移动时,在△EBF和△FCG中,∠B=∠C=90°,
①若=,即=,
解得t=.
所以当t=时,△EBF∽△FCG,
②若=即=,解得t=.
所以当t=时,△EBF∽△GCF.
综上所述,当t=或t=时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
21.解:(1)设经过x秒后,△AMN的面积等于矩形ABCD面积的,
则有:(6﹣2x)x=×3×6,即x2﹣3x+2=0,
解方程,得x1=1,x2=2,
经检验,可知x1=1,x2=2符合题意,
所以经过1秒或2秒后,△AMN的面积等于矩形ABCD面积的.
(2)假设经过t秒时,以A,M,N为顶点的三角形与△ACD相似,
由矩形ABCD,可得∠CDA=∠MAN=90°,
因此有或
即①,或②
解①,得t=;解②,得t=
经检验,t=或t=都符合题意,
所以动点M,N同时出发后,经过秒或秒时,以A,M,N为顶点的三角形与△ACD相似.
一.选择题(共8小题,满分40分)
1.已知△ABC和△DEF中,∠B=∠E=100°,下列条件不能得到两个三角形相似的是( )
A.∠A=∠D B.=
C.∠C=∠D D.∠C=40°,∠D=30°
2.如图,在△ABC中,∠B=80°,∠C=40°,直线l平行于BC.现将直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,若△AMN与△ABC相似,则旋转角为( )
A.20° B.40° C.60° D.80°
3.若如图所示的两个四边形相似,则∠α的度数是( )
A.80° B.60° C.70° D.150°
4.如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,且AP=2.8,过点P沿直线剪下一个与△ABC相似的小三角形纸板,则不同的剪法有( )
A.2种 B.3种 C.4种 D.5种
5.如图,△ABC中,DE∥BC,=,△ADE的面积是2,那么△BEC的面积是( )
A.6 B.8 C.12 D.18
6.如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=AE EG;④若AB=4,AD=5,则CE=1.
A.①②③④ B.①②③ C.①③④ D.①②
7.如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在格点上(小正方形的顶点).P1,P2,P3,P4,P5是△DEF边上的5个格点,请在这5个格点中选取2个作为三角形的顶点,使它和点D构成的三角形与△ABC相似,所有符合条件的三角形的个数为( )
A.2个 B.3个 C.4个 D.5个
8.如图,正方形ABCD中,以BC为边向正方形内部作等边△BCE,连接AE并延长交CD于F,连接DE,下列结论:①AE=DE;②∠CEF=45°;③AE=EF;④△DEF∽△ABE,其中正确的结论共有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,满分40分)
9.如图,在△ABC中,D,E分别是AB,AC上的点(DE≠BC),使△ADE∽△ACB的一个条件可以是 .
10.如图,矩形ABCD∽BCFE,且AE=3,AD=2,则BE的长为 .
11.等边三角形ABC和△A′B′C′相似,相似比为5:2,若AB=10,B′C′边上的高是 .
12.如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1,S2,S3,S4,以下判断:
①PA+PB+PC+PD的最小值为10;
②若△PAB≌△PCD,则△PAD≌△PBC;
③若S1=S2,则S3=S4,
④若△PAB∽△PDA,则PA=2
其中正确的是 (把所有正确的结论的序号都填在横线上).
13.如图,在 ABCD中,E为AD的三等分点,AE=AD,连接BE,交AC于点F,AC=15,则AF为 .
14.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,且CE∥BD,并测得
BC=4m,CA=1m,那么树BD的高度是 m.
15.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
16.如图,Rt△ABC中,∠BAC=90°,AD⊥BC,若BD=1,AD=3,则CD= .
三.解答题(共5小题,满分40分)
17.在正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P.
(1)求PD的长;
(2)点E在DC上,点F在DP上,且∠DFE=45°.若PF=,求CE的长.
18.如图,洋洋和华华用所学的数学知识测量一条小河的宽度,河的对岸有一棵大树,底部记为点A,在他们所在的岸边选择了点B,并且使AB与河岸垂直,在B处与地面垂直竖起标杆BC,再在AB的延长线上选择点D,与地面垂直竖起标杆DE,使得A、C、E三点共线.经测量,BC=1m,DE=1.5m,BD=5m,求小河的宽度.
19.已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
20.如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动.点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2)
(1)当t=1秒时,S的值是多少?
(2)写出S和t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点E、B、F为顶点的三角形与以点F、C、G为顶点的三角形相似?请说明理由.
21.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:
(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.
参考答案
一.选择题(共8小题,满分40分)
1.解:在△ABC和△DEF中,∠B=∠E=100°,
A、当∠A=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
B、当时,△ABC∽△DEF,故能判定这两个三角形相似;
C、当∠C=∠D时,△ABC∽△DEF,故能判定这两个三角形相似;
D、当∠C=40°,∠D=30°时,不能判断这两个三角形相似.
故选:D.
2.解:如图,直线l绕点A逆时针旋转,所得直线分别交边AB和AC于点M、N,
若△AMN∽△ACB,则∠AMN=∠C=40°,
又∵直线l平行于BC,
∴∠ADE=∠B=80°,
∴∠DFM=∠ADE﹣∠AMN=80°﹣40°=40°,
即直线l旋转前后的夹角为40°,
∴旋转角为40°,
故选:B.
3.解:如图,
∵四边形ABCD∽四边形A′B′C′D′,
∴∠A=∠A′=150°,
∵∠B′=∠B=60°,∠C′=∠C=80°,
∴∠α=360°﹣∠A′﹣∠B′﹣∠C′=70°.
故选:C.
4.解:如图所示,过P作PD∥AB交BC于D或PE∥BC交AB于E,则△PCD∽△ACB或△APE∽△ACB,
如图所示,过P作∠APF=∠B交AB于F,则△APF∽△ABC,
故选:B.
5.解:∵△ABC中,DE∥BC,=,△ADE的面积是2,
∴△BDE的面积是4,
∴△ADE∽△ABC,
∴,
∴△ABC的面积=18,
∴△BEC的面积=18﹣2﹣4=12,
故选:C.
6.解:①由折叠可得,AD=AF,DG=FG,
在△ADG和△AFG中,
,
∴△ADG≌△AFG(SSS),
∴∠ADG=∠AFG,故①正确;
②∵GF∥DC,
∴∠EGF=∠DEG,
由翻折的性质可知:GD=GF,DE=EF,∠DGE=∠EGF,
∴∠DGE=∠DEG,
∴GD=DE,
∴DG=GF=DE=EF,
∴四边形DEFG为菱形,故②正确;
③如图所示,连接DF交AE于O,
∵四边形DEFG为菱形,
∴GE⊥DF,OG=OE=GE,
∵∠DOE=∠ADE=90°,∠OED=∠DEA,
∴△DOE∽△ADE,
∴=,即DE2=EO AE,
∵EO=GE,DE=DG,
∴DG2=AE EG,故③正确;
④由折叠可得,AF=AD=5,
∴Rt△ABF中,BF==3,
∴CF=5﹣3=2,
设CE=x,则DE=EF=4﹣x,
∵Rt△CEF中,CE2+CF2=EF2,
∴x2+22=(4﹣x)2,
解得x=,
∴CE=,故④错误;
故选:B.
7.解:设网格的边长为1.
则AC=,AB=,BC=.
连接P2P5,
DP5=,DP2=,P2P5=.
∵,
∴△ACB∽△DP5P2.
同理可找到△DP2P4,△DP4P5和△ACB相似.
故选:B.
8.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠DAB=∠ABC=∠BCD=∠ADC=90°,
∵△EBC是等边三角形,
∴BC=BE=CE,∠EBC=∠EBC=∠ECB=60°,
∴∠ABE=∠ECF=30°,
∵BA=BE,EC=CD,
∴∠BAE=∠BEA=∠CED=∠CDE=(180°﹣30°)=75°,
∴∠EAD=∠EDA=15°,
∴EA=ED,故①正确,
∴∠DEF=∠EAD+∠ADE=30°,
∴∠CEF=∠CED﹣∠DEF=45°,故②正确,
∵∠EDF=∠AFD=75°,
∴ED=EF,
∴AE=EF,故③正确,
∵∠BAE=∠BEA=∠EDF=∠EFD=75°,
∴△DEF∽△ABE,故④正确,
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵∠A=∠A
∴当∠ADE=∠C或∠AED=∠B或= 时,△ADE∽△ABC,
故答案为:∠ADE=∠C或∠AED=∠B或=.
10.解:∵四边形ABCD和四边形BCFE是矩形,
∴BC=EF=AD=2,
∵矩形ABCD∽BCFE,
∴=,
∴=,
∴BE=1(负值舍去),
故答案为:1.
11.解:∵△ABC是等边三角形,且AB=10,
∴BC边上的高为5,
∵△ABC∽△A′B′C′,且相似比为5:2,
∴B′C′边上的高是2.
12.解:①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PCD,则PA=PC,PB=PD,所以P在线段AC、BD的垂直平分线上,即P是矩形ABCD两对角线的交点,所以△PAD≌△PBC,故②正确;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB∽△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°﹣(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④错误.
故答案为①②③.
13.解:在 ABCD中,AD=BC,AD∥BC,
∵E为AD的三等分点,
∴AE=AD=BC,
∵AD∥BC,
∴==,
∵AC=15,
∴AF=×15=6.
故答案为6.
14.解:∵EC∥AB,BD⊥AB,
∴EC∥BD,∠ACE=∠ABD=90°,
在Rt△ACE∽Rt△ABD中,∠A=∠A,∠ACE=∠ABD=90°,
∴Rt△ACE∽Rt△ABD,
∴,即,解得BD=10m.
故答案为:10
15.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
16.解:∵Rt△ABC中,∠BAC=90°,
∴∠B+∠C=90°.
∵AD⊥BC于点D,
∴∠B+∠BAD=90°,∠C+∠CAD=90°,
∴∠BAD=∠C,∠B=∠CAD,
∴△ABD∽△CAD,
∴AD2=BD CD,
∵BD=1,AD=3,
∴CD=9,
故答案为:9
三.解答题(共5小题,满分40分)
17.解:(1)如图作PK⊥AD于K,PH⊥AB于H.
∵四边形ABCD是正方形,
∴∠PAD=∠PAB=45°,
∵PK⊥AD,PH⊥AB,
∴PK=PH,
∴===,
∴AB=AD=2,AM=BM=1,
∴DM=,
∴=2,
∴PD=×=.
(2)∵PF=,PD=,DM=,
∴DF=,PM=,
∵DE∥AM,
∴∠AMP=∠EDF,
∵∠DFE=∠MAP=45°,
∴△AMP∽△FDE,
∴=,
∴=,
∴DE=,
∴EC=2﹣=.
18.解:设小河的宽度AB=xm,根据题意得:BC⊥AD,ED⊥AD,
∴△ABC∽△ADE,
∴AB:AD=BC:ED,
∴x:(x+5)=1:1.5,
解得x=10,∴AB=10,
即小河的宽度为10米.
19.(1)证明:∵PQ⊥AQ,
∴∠AQP=90°=∠ABC,
在△APQ与△ABC中,
∵∠AQP=90°=∠ABC,∠A=∠A,
∴△AQP∽△ABC.
(2)解:在Rt△ABC中,AB=3,BC=4,由勾股定理得:AC=5.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,
(I)当点P在线段AB上时,如题图1所示.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ,
由(1)可知,△AQP∽△ABC,
∴,即,解得:PB=,
∴AP=AB﹣PB=3﹣=;
(II)当点P在线段AB的延长线上时,如题图2所示.
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是PB=BQ.
∵BP=BQ,∴∠BQP=∠P,
∵∠BQP+∠AQB=90°,∠A+∠P=90°,
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AP中点,
∴AP=2AB=2×3=6.
综上所述,当△PQB为等腰三角形时,AP的长为或6.
20.解:(1)如图1,当t=1秒时,AE=2,EB=10,BF=4,FC=4,CG=2,
由S=S梯形GCBE﹣S△EBF﹣S△FCG,
=×﹣
=×(10+2)×8﹣×10×4﹣
=24(cm2);
(2)①如图1,当0≤t≤2时,点E、F、G分别在边AB、BC、CD上移动,
此时AE=2t,EB=12﹣2t,BF=4t,FC=8﹣4t,CG=2t,
S=S梯形GCBE﹣S△EBF﹣S△FCG
=×(EB+CG) BC﹣EB BF﹣FC CG
=×8×(12﹣2t+2t)﹣×4t(12﹣2t)﹣×2t(8﹣4t)
=8t2﹣32t+48(0≤t≤2).
②如图2,当点F追上点G时,4t=2t+8,解得t=4,
当2<t<4时,点E在边AB上移动,点F、G都在边CD上移动,此时CF=4t﹣8,CG=2t,
FG=CG﹣CF=2t﹣(4t﹣8)=8﹣2t,
S=FG BC=(8﹣2t) 8=﹣8t+32.
即S=﹣8t+32(2<t<4).
(3)如图1,当点F在矩形的边BC上的边移动时,在△EBF和△FCG中,∠B=∠C=90°,
①若=,即=,
解得t=.
所以当t=时,△EBF∽△FCG,
②若=即=,解得t=.
所以当t=时,△EBF∽△GCF.
综上所述,当t=或t=时,以点E、B、F为顶点的三角形与以F、C、G为顶点的三角形相似.
21.解:(1)设经过x秒后,△AMN的面积等于矩形ABCD面积的,
则有:(6﹣2x)x=×3×6,即x2﹣3x+2=0,
解方程,得x1=1,x2=2,
经检验,可知x1=1,x2=2符合题意,
所以经过1秒或2秒后,△AMN的面积等于矩形ABCD面积的.
(2)假设经过t秒时,以A,M,N为顶点的三角形与△ACD相似,
由矩形ABCD,可得∠CDA=∠MAN=90°,
因此有或
即①,或②
解①,得t=;解②,得t=
经检验,t=或t=都符合题意,
所以动点M,N同时出发后,经过秒或秒时,以A,M,N为顶点的三角形与△ACD相似.
