2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.2相似三角形 同步达标训练 (Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 300.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 09:12:30 | ||
图片预览

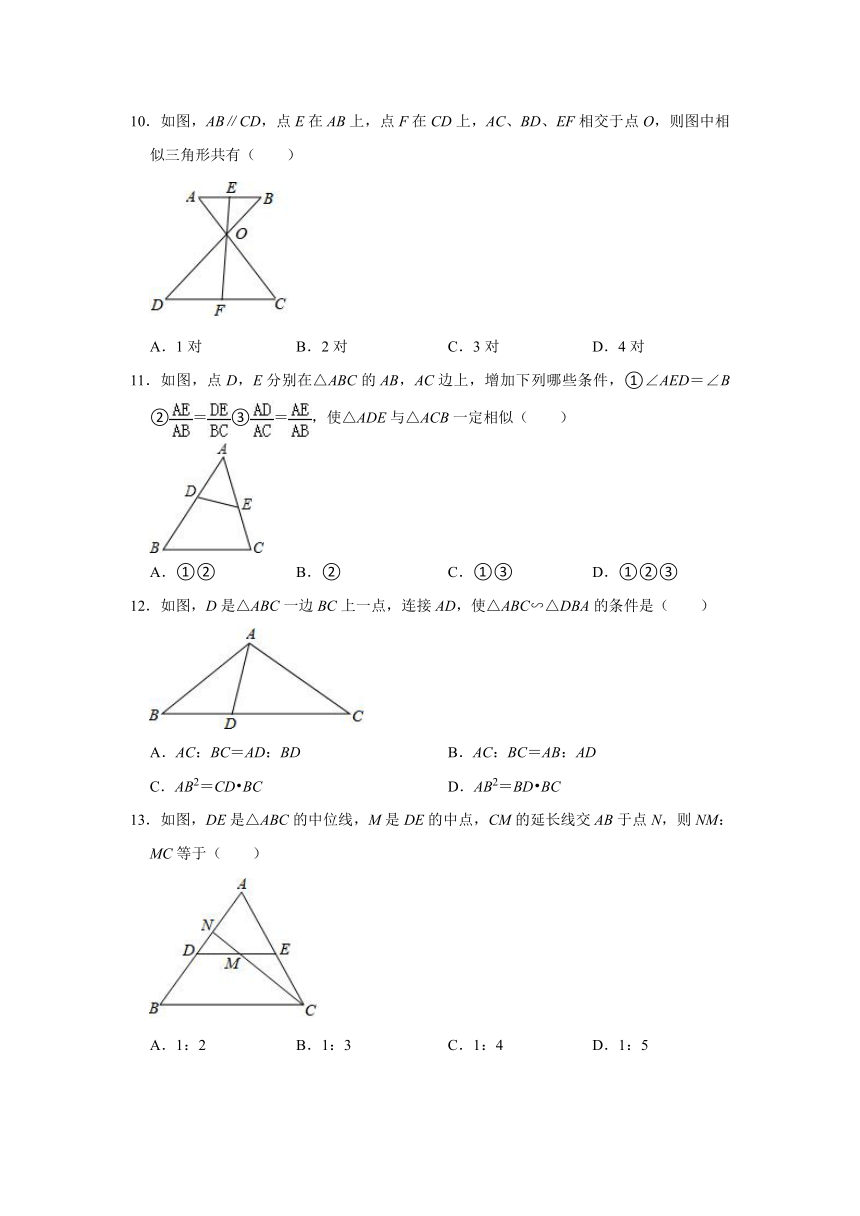

文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》同步达标训练(附答案)
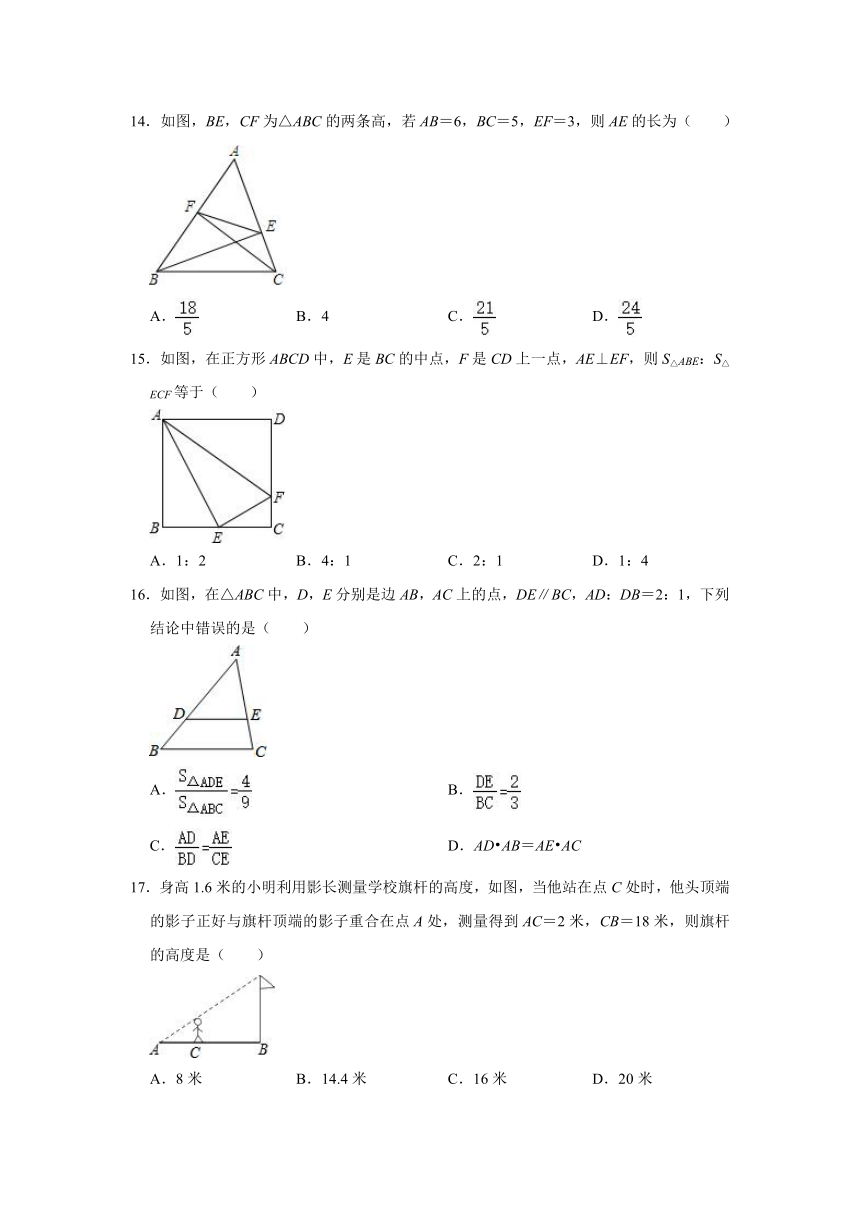
1.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
2.若四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,AB=8cm,A′B′=6cm,AD=5cm,则A′D′等于( )
A.cm B.cm C.cm D.cm
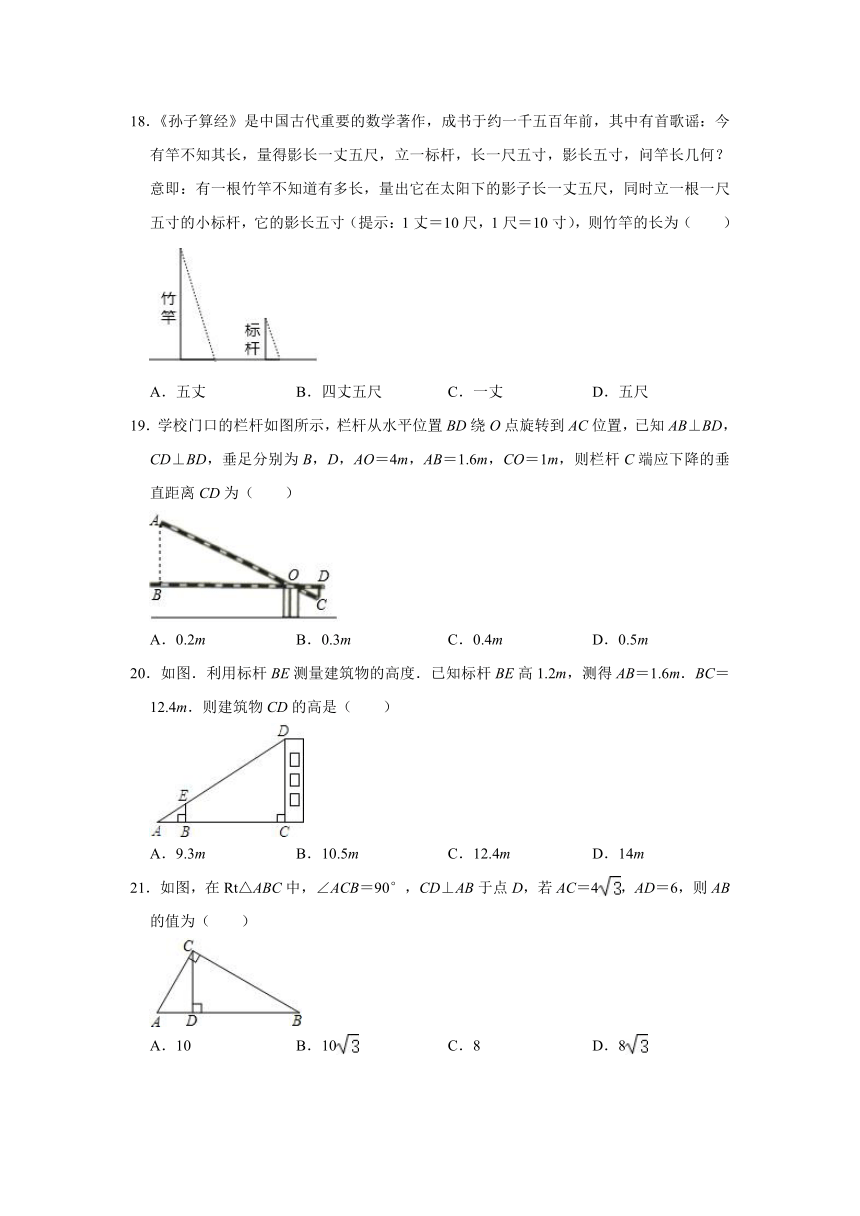
3.如图,已知矩形ABCD中,AB=3,BE=2,EF⊥BC.若四边形EFDC与四边形BEFA相似而不全等,则CE=( )
A.3 B.3.5 C.4 D.4.5
4.如果两个相似多边形的面积比为4:9,那么它们的周长比为( )
A.4:9 B.2:3 C.: D.16:81
5.若△ABC∽△DEF,△ABC与△DEF的面积之比为4:25,则△ABC与△DEF周长之比为( )A.4:25 B.2:5 C.5:2 D.25:4
6.如果两个相似三角形对应高的比是4:9,那么它们的面积比是( )
A.4:9 B.2:3 C.16:81 D.9:4
7.已知△ABC∽△DEF,相似比为2,且△ABC的周长为16,则△DEF的周长为( )
A.2 B.4 C.8 D.32
8.两个相似三角形的最短边分别为5cm和3cm,他们的周长之差为12cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
9.如图,点E为平行四边形ABCD边BC延长线上的一点,连接AE与CD相交于点F.则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
10.如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
11.如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,①∠AED=∠B②=③=,使△ADE与△ACB一定相似( )
A.①② B.② C.①③ D.①②③
12.如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
A.AC:BC=AD:BD B.AC:BC=AB:AD
C.AB2=CD BC D.AB2=BD BC
13.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM:MC等于( )
A.1:2 B.1:3 C.1:4 D.1:5
14.如图,BE,CF为△ABC的两条高,若AB=6,BC=5,EF=3,则AE的长为( )
A. B.4 C. D.
15.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则S△ABE:S△ECF等于( )
A.1:2 B.4:1 C.2:1 D.1:4
16.如图,在△ABC中,D,E分别是边AB,AC上的点,DE∥BC,AD:DB=2:1,下列结论中错误的是( )
A. B.
C. D.AD AB=AE AC
17.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( )
A.8米 B.14.4米 C.16米 D.20米
18.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
19.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.3m C.0.4m D.0.5m
20.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
21.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=4,AD=6,则AB的值为( )
A.10 B.10 C.8 D.8
22.已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.
23.如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若AC BD=AD BC,
①求证:△ACD∽△BCE;
②求的值.
24.在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EA EC;
(2)若ED=6,BD=CD=3,求BC的长.
25.如图在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)如AF=3,AG=5,求△ADE与△ABC的周长之比.
参考答案
1.解:3m×2m=6m2,
∴长方形广告牌的成本是120÷6=20元/m2,
将此广告牌的四边都扩大为原来的3倍,
则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54m2,
∴扩大后长方形广告牌的成本是54×20=1080元,
故选:C.
2.解:∵四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,
∴=,
∵AB=8cm,A′B′=6cm,AD=5cm,
∴=,
则A′D′=.
故选:B.
3.解:设CE=x,
∵四边形EFDC与四边形BEFA相似,
∴,
∵AB=3,BE=2,EF=AB,
∴,
解得:x=4.5,
故选:D.
4.解:∵两个相似多边形面积的比为4:9,
∴两个相似多边形周长的比等于2:3,
∴这两个相似多边形周长的比是2:3.
故选:B.
5.解:∵相似三角形△ABC与△DEF面积的比为4:25,
∴它们的相似比为2:5,
∴△ABC与△DEF的周长比为2:5.
故选:B.
6.解:∵两个相似三角形对应高之比为4:9,
∴它们的相似比为4:9,
∴面积比=()2=16:81.
故选:C.
7.解:设△DEF的周长为x,
∵△ABC∽△DEF,相似比为2,
∴16:x=2:1,
解得,x=8.
故选:C.
8.解:根据题意得两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x﹣3x=12,
解得x=6,
所以5x=30,
即大三角形的周长为30cm.
故选:D.
9.解:在平行四边形ABCD中,AB∥CD,BC∥AD,
所以,△ABE∽△FCE,△FCE∽△ADF,△ADF∽△ABE,
共3对.
故选:C.
10.解:∵AB∥CD,
∴△AEO∽△CFO,△BEO∽△DFO,△ABO∽△CDO,
故选:C.
11.解:∵∠A=∠A,∠AED=∠B,
∴△AED∽△ABC,故①正确,
∵∠A=∠A,=,
∴△AED∽△ABC,故③正确,
由②无法判定△ADE与△ACB相似,
故选:C.
12.解:∵∠B=∠B,
∴当=时,
△ABC∽△DBA,
当AB2=BD BC时,△ABC∽△DBA,
故选:D.
13.解:∵DE是△ABC的中位线,M是DE的中点,
∴DM∥BC,DM=ME=BC.
∴△NDM∽△NBC,==.
∴=.
故选:B.
14.解:∵BE,CF为△ABC的两条高,
∴∠AEB=∠AFC=90°,
∵∠A=∠A,
∴△AEB∽△AFC,
∴=,
∵∠A=∠A,
∴△AEF∽△ABC,
∴=,
∵AB=6,BC=5,EF=3,
∴=,
∴AE=,
故选:A.
15.解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
∴△BAE∽△CEF,
∴S△ABE:S△ECF=AB2:CE2,
∵E是BC的中点,
∴BC=2CE=AB
∴==,即S△ABE:S△ECF=4:1
故选:B.
16.解:∵DE∥BC,AD:DB=2:1,
∴△ADE∽△ABC,
∴==,=,
∴=()2=,
∴A、B、C正确,
故选:D.
17.解:设旗杆高度为h,
由题意得=,
解得:h=16米.
故选:C.
18.解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴,解得x=45(尺).
故选:B.
19.解:∵AB⊥BD,CD⊥BD,
∴∠ABO=∠CDO=90°,
又∵∠AOB=∠COD,
∴△ABO∽△CDO,
则=,
∵AO=4m,AB=1.6m,CO=1m,
∴=,
解得:CD=0.4m,
故选:C.
20.解:∵EB∥CD,
∴△ABE∽△ACD,
∴=,即=,
∴CD=10.5(米).
故选:B.
21.解:如图,∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD AB,
又∵AC=4,AD=6,
∴(4)2=6×AB,
∴AB=8.
故选:C.
22.解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),
PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4),
PC⊥OB时,△CPB∽△OAB,根据勾股定理得,OB==10,
∵P(3,4)为OB的中点,
∴PB=OB=5,
∴=,
即=,
解得BC=,
AC=AB﹣BC=8﹣=,
此时点C的坐标为(6,),
综上所述,点C的坐标为(3,0),(6,4),(6,).
23.证明:(1)如图1,延长CD交AB于E,
∵∠ADE=∠CAD+∠ACD,
∠BDE=∠CBD+∠BCD,
∴∠ADB=∠ADE+∠BDE=∠CAD+∠CBD+∠ACB,
∵∠ADB=∠ACB+90°.
∴∠CAD+∠CBD=90°;
(2)①如图2,∵∠CAD+∠CBD=90°,∠CBD+∠CBE=90°,
∴∠CAD=∠CBE,
∵AC BD=AD BC,BD=BE,
∴,
∴△ACD∽△BCE;
②如图2,连接DE,
∵BE⊥BD,BE=BD,
∴△BDE是等腰直角三角形,
∴=,
∵△ACD∽△BCE,
∴∠ACD=∠BCE,
∴∠ACB=∠DCE,
∵,
∴△ACB∽△DCE,
∴,
∴====.
24.(1)证明:∵EF是BD的垂直平分线,
∴EB=ED,
∴∠EDB=∠EBD,
∵∠EDB=∠C+∠DBC,∠EBD=∠ABE+∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=∠ABE,
∵∠BEC=∠BEA,
∴△EAB∽△EBC,
∴,
∴EB2=EA EC,
∵EB=ED,
∴ED2=EA EC;
(2)解法一:∵ED=EB=6,BD=CD=3,
∴EC=6+3=9,
由(1)知:ED2=EA EC;
∴EA=4,
如右图,过A作AG⊥EB于G,过D作DH⊥EB于H,
Rt△EFD中,ED=6,DF=,
∴EF==,
∴S△EBD=EB DH=BD EF,
∴DH=EF=,
∵AG∥DH,
∴△AGE∽△DHE,
∴==,
∴=,AG=,
由勾股定理得:EG===,
∴BG=6﹣=,
由勾股定理得:AB===,
∵△EAB∽△EBC,
∴,
∴,
∴BC=.
解法二:根据解法一得:AE=4,
∴AD=2,AC=5,
∵BD=CD,
∴∠DBC=∠DCB,
∴∠BAD=∠BAC,
∴△ABD∽△ACB,
∴,
∴,
∴AB=,BC=.
25.解:(1)∵AG⊥BC,AF⊥DE,
∴∠AFE=∠AGC=90°,
∵∠EAF=∠GAC,
∴∠AED=∠ACB,
∵∠EAD=∠BAC,
∴△ADE∽△ABC;
(2)由(1)可得△ADE∽△ABC,
又∵AG⊥BC于点G,AF⊥DE于点F,
∴△ADE与△ABC的周长之比==.
1.制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )
A.360元 B.720元 C.1080元 D.2160元
2.若四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,AB=8cm,A′B′=6cm,AD=5cm,则A′D′等于( )
A.cm B.cm C.cm D.cm
3.如图,已知矩形ABCD中,AB=3,BE=2,EF⊥BC.若四边形EFDC与四边形BEFA相似而不全等,则CE=( )
A.3 B.3.5 C.4 D.4.5
4.如果两个相似多边形的面积比为4:9,那么它们的周长比为( )
A.4:9 B.2:3 C.: D.16:81
5.若△ABC∽△DEF,△ABC与△DEF的面积之比为4:25,则△ABC与△DEF周长之比为( )A.4:25 B.2:5 C.5:2 D.25:4
6.如果两个相似三角形对应高的比是4:9,那么它们的面积比是( )
A.4:9 B.2:3 C.16:81 D.9:4
7.已知△ABC∽△DEF,相似比为2,且△ABC的周长为16,则△DEF的周长为( )
A.2 B.4 C.8 D.32
8.两个相似三角形的最短边分别为5cm和3cm,他们的周长之差为12cm,那么大三角形的周长为( )
A.14 cm B.16 cm C.18 cm D.30 cm
9.如图,点E为平行四边形ABCD边BC延长线上的一点,连接AE与CD相交于点F.则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
10.如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
11.如图,点D,E分别在△ABC的AB,AC边上,增加下列哪些条件,①∠AED=∠B②=③=,使△ADE与△ACB一定相似( )
A.①② B.② C.①③ D.①②③
12.如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
A.AC:BC=AD:BD B.AC:BC=AB:AD
C.AB2=CD BC D.AB2=BD BC
13.如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于点N,则NM:MC等于( )
A.1:2 B.1:3 C.1:4 D.1:5
14.如图,BE,CF为△ABC的两条高,若AB=6,BC=5,EF=3,则AE的长为( )
A. B.4 C. D.
15.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则S△ABE:S△ECF等于( )
A.1:2 B.4:1 C.2:1 D.1:4
16.如图,在△ABC中,D,E分别是边AB,AC上的点,DE∥BC,AD:DB=2:1,下列结论中错误的是( )
A. B.
C. D.AD AB=AE AC
17.身高1.6米的小明利用影长测量学校旗杆的高度,如图,当他站在点C处时,他头顶端的影子正好与旗杆顶端的影子重合在点A处,测量得到AC=2米,CB=18米,则旗杆的高度是( )
A.8米 B.14.4米 C.16米 D.20米
18.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺 C.一丈 D.五尺
19.学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A.0.2m B.0.3m C.0.4m D.0.5m
20.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是( )
A.9.3m B.10.5m C.12.4m D.14m
21.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,若AC=4,AD=6,则AB的值为( )
A.10 B.10 C.8 D.8
22.已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.
23.如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若AC BD=AD BC,
①求证:△ACD∽△BCE;
②求的值.
24.在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于点E.
(1)求证:ED2=EA EC;
(2)若ED=6,BD=CD=3,求BC的长.
25.如图在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)如AF=3,AG=5,求△ADE与△ABC的周长之比.
参考答案
1.解:3m×2m=6m2,
∴长方形广告牌的成本是120÷6=20元/m2,
将此广告牌的四边都扩大为原来的3倍,
则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54m2,
∴扩大后长方形广告牌的成本是54×20=1080元,
故选:C.
2.解:∵四边形ABCD与四边形A′B′C′D′相似,AB与A′B′,AD与A′D′分别是对应边,
∴=,
∵AB=8cm,A′B′=6cm,AD=5cm,
∴=,
则A′D′=.
故选:B.
3.解:设CE=x,
∵四边形EFDC与四边形BEFA相似,
∴,
∵AB=3,BE=2,EF=AB,
∴,
解得:x=4.5,
故选:D.
4.解:∵两个相似多边形面积的比为4:9,
∴两个相似多边形周长的比等于2:3,
∴这两个相似多边形周长的比是2:3.
故选:B.
5.解:∵相似三角形△ABC与△DEF面积的比为4:25,
∴它们的相似比为2:5,
∴△ABC与△DEF的周长比为2:5.
故选:B.
6.解:∵两个相似三角形对应高之比为4:9,
∴它们的相似比为4:9,
∴面积比=()2=16:81.
故选:C.
7.解:设△DEF的周长为x,
∵△ABC∽△DEF,相似比为2,
∴16:x=2:1,
解得,x=8.
故选:C.
8.解:根据题意得两三角形的周长的比为5:3,
设两三角形的周长分别为5xcm,3xcm,
则5x﹣3x=12,
解得x=6,
所以5x=30,
即大三角形的周长为30cm.
故选:D.
9.解:在平行四边形ABCD中,AB∥CD,BC∥AD,
所以,△ABE∽△FCE,△FCE∽△ADF,△ADF∽△ABE,
共3对.
故选:C.
10.解:∵AB∥CD,
∴△AEO∽△CFO,△BEO∽△DFO,△ABO∽△CDO,
故选:C.
11.解:∵∠A=∠A,∠AED=∠B,
∴△AED∽△ABC,故①正确,
∵∠A=∠A,=,
∴△AED∽△ABC,故③正确,
由②无法判定△ADE与△ACB相似,
故选:C.
12.解:∵∠B=∠B,
∴当=时,
△ABC∽△DBA,
当AB2=BD BC时,△ABC∽△DBA,
故选:D.
13.解:∵DE是△ABC的中位线,M是DE的中点,
∴DM∥BC,DM=ME=BC.
∴△NDM∽△NBC,==.
∴=.
故选:B.
14.解:∵BE,CF为△ABC的两条高,
∴∠AEB=∠AFC=90°,
∵∠A=∠A,
∴△AEB∽△AFC,
∴=,
∵∠A=∠A,
∴△AEF∽△ABC,
∴=,
∵AB=6,BC=5,EF=3,
∴=,
∴AE=,
故选:A.
15.解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=BC=CD,
∵AE⊥EF,
∴∠AEF=∠B=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠FEC=90°,
∴∠BAE=∠CEF,
∴△BAE∽△CEF,
∴S△ABE:S△ECF=AB2:CE2,
∵E是BC的中点,
∴BC=2CE=AB
∴==,即S△ABE:S△ECF=4:1
故选:B.
16.解:∵DE∥BC,AD:DB=2:1,
∴△ADE∽△ABC,
∴==,=,
∴=()2=,
∴A、B、C正确,
故选:D.
17.解:设旗杆高度为h,
由题意得=,
解得:h=16米.
故选:C.
18.解:设竹竿的长度为x尺,
∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,
∴,解得x=45(尺).
故选:B.
19.解:∵AB⊥BD,CD⊥BD,
∴∠ABO=∠CDO=90°,
又∵∠AOB=∠COD,
∴△ABO∽△CDO,
则=,
∵AO=4m,AB=1.6m,CO=1m,
∴=,
解得:CD=0.4m,
故选:C.
20.解:∵EB∥CD,
∴△ABE∽△ACD,
∴=,即=,
∴CD=10.5(米).
故选:B.
21.解:如图,∵在Rt△ABC中,∠ACB=90°,CD⊥AB,
∴AC2=AD AB,
又∵AC=4,AD=6,
∴(4)2=6×AB,
∴AB=8.
故选:C.
22.解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),
PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4),
PC⊥OB时,△CPB∽△OAB,根据勾股定理得,OB==10,
∵P(3,4)为OB的中点,
∴PB=OB=5,
∴=,
即=,
解得BC=,
AC=AB﹣BC=8﹣=,
此时点C的坐标为(6,),
综上所述,点C的坐标为(3,0),(6,4),(6,).
23.证明:(1)如图1,延长CD交AB于E,
∵∠ADE=∠CAD+∠ACD,
∠BDE=∠CBD+∠BCD,
∴∠ADB=∠ADE+∠BDE=∠CAD+∠CBD+∠ACB,
∵∠ADB=∠ACB+90°.
∴∠CAD+∠CBD=90°;
(2)①如图2,∵∠CAD+∠CBD=90°,∠CBD+∠CBE=90°,
∴∠CAD=∠CBE,
∵AC BD=AD BC,BD=BE,
∴,
∴△ACD∽△BCE;
②如图2,连接DE,
∵BE⊥BD,BE=BD,
∴△BDE是等腰直角三角形,
∴=,
∵△ACD∽△BCE,
∴∠ACD=∠BCE,
∴∠ACB=∠DCE,
∵,
∴△ACB∽△DCE,
∴,
∴====.
24.(1)证明:∵EF是BD的垂直平分线,
∴EB=ED,
∴∠EDB=∠EBD,
∵∠EDB=∠C+∠DBC,∠EBD=∠ABE+∠ABD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠C=∠ABE,
∵∠BEC=∠BEA,
∴△EAB∽△EBC,
∴,
∴EB2=EA EC,
∵EB=ED,
∴ED2=EA EC;
(2)解法一:∵ED=EB=6,BD=CD=3,
∴EC=6+3=9,
由(1)知:ED2=EA EC;
∴EA=4,
如右图,过A作AG⊥EB于G,过D作DH⊥EB于H,
Rt△EFD中,ED=6,DF=,
∴EF==,
∴S△EBD=EB DH=BD EF,
∴DH=EF=,
∵AG∥DH,
∴△AGE∽△DHE,
∴==,
∴=,AG=,
由勾股定理得:EG===,
∴BG=6﹣=,
由勾股定理得:AB===,
∵△EAB∽△EBC,
∴,
∴,
∴BC=.
解法二:根据解法一得:AE=4,
∴AD=2,AC=5,
∵BD=CD,
∴∠DBC=∠DCB,
∴∠BAD=∠BAC,
∴△ABD∽△ACB,
∴,
∴,
∴AB=,BC=.
25.解:(1)∵AG⊥BC,AF⊥DE,
∴∠AFE=∠AGC=90°,
∵∠EAF=∠GAC,
∴∠AED=∠ACB,
∵∠EAD=∠BAC,
∴△ADE∽△ABC;
(2)由(1)可得△ADE∽△ABC,
又∵AG⊥BC于点G,AF⊥DE于点F,
∴△ADE与△ABC的周长之比==.
