2021-2022学年人教版九年级数学下册27.3位似 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.3位似 同步达标测评(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 334.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 09:15:26 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《27.3位似》同步达标测评(附答案)
一.选择题(共8小题,满分40分)
1.如图,△ABC与△A'B'C'位似,点O是它们的位似中心,其中BC=2B'C',若点A的坐标为(4,2),则A'O的长度为( )
A. B. C. D.
2.如图,在平面直角坐标系中,已知△ABC点A(﹣2,3),C(﹣1,2),以原点O为位似中心,在第二象限内将△ABC各边扩大为原来的2倍,再绕原点O顺时针旋转90°得到△A′B′C′,则变换后的点A的对应点A′的坐标为( )
A.(2,6) B.(4,2) C.(3,2) D.(6,4)
3.已知点A(0,3),B(﹣4,3),以原点O为位似中心,把线段AB缩短为原来的,其中点C与点A对应,点D与点B对应.则点D的坐标为( )
A.(﹣1,) B.(1,﹣)
C.(,﹣1)或(﹣,1) D.(﹣1,)或(1,﹣)
4.如图,△ABO缩小后变为△A'B'O,其中A、B的对应点分别为A'、B',点A、B、A'、B'均在格点上,若线段AB上有点P(m,n),则点P在A'B'上的对应点P'的坐标为( )
A.(,n) B.(m,n) C.(m,) D.()
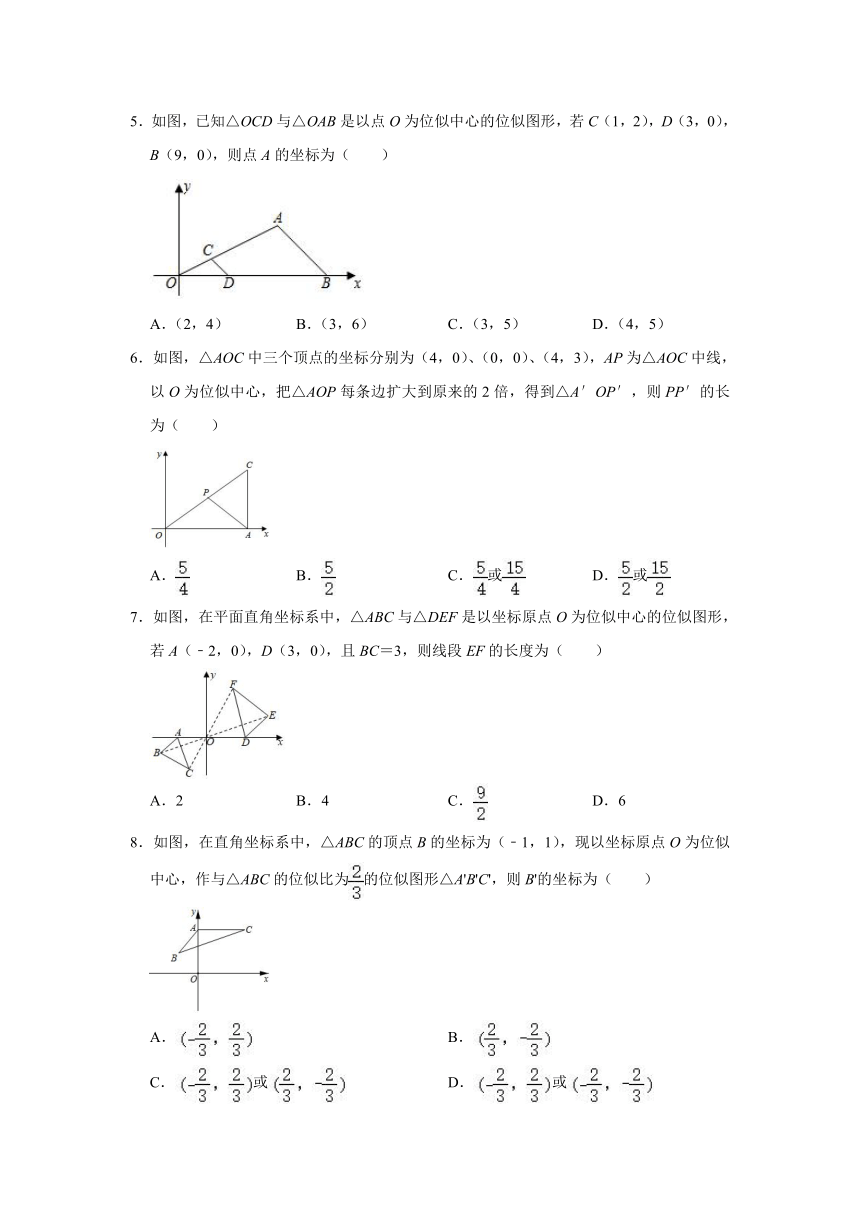
5.如图,已知△OCD与△OAB是以点O为位似中心的位似图形,若C(1,2),D(3,0),B(9,0),则点A的坐标为( )
A.(2,4) B.(3,6) C.(3,5) D.(4,5)
6.如图,△AOC中三个顶点的坐标分别为(4,0)、(0,0)、(4,3),AP为△AOC中线,以O为位似中心,把△AOP每条边扩大到原来的2倍,得到△A′OP′,则PP′的长为( )
A. B. C.或 D.或
7.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且BC=3,则线段EF的长度为( )
A.2 B.4 C. D.6
8.如图,在直角坐标系中,△ABC的顶点B的坐标为(﹣1,1),现以坐标原点O为位似中心,作与△ABC的位似比为的位似图形△A'B'C',则B'的坐标为( )
A. B.
C.或 D.或
二.填空题(共9小题,满分45分)
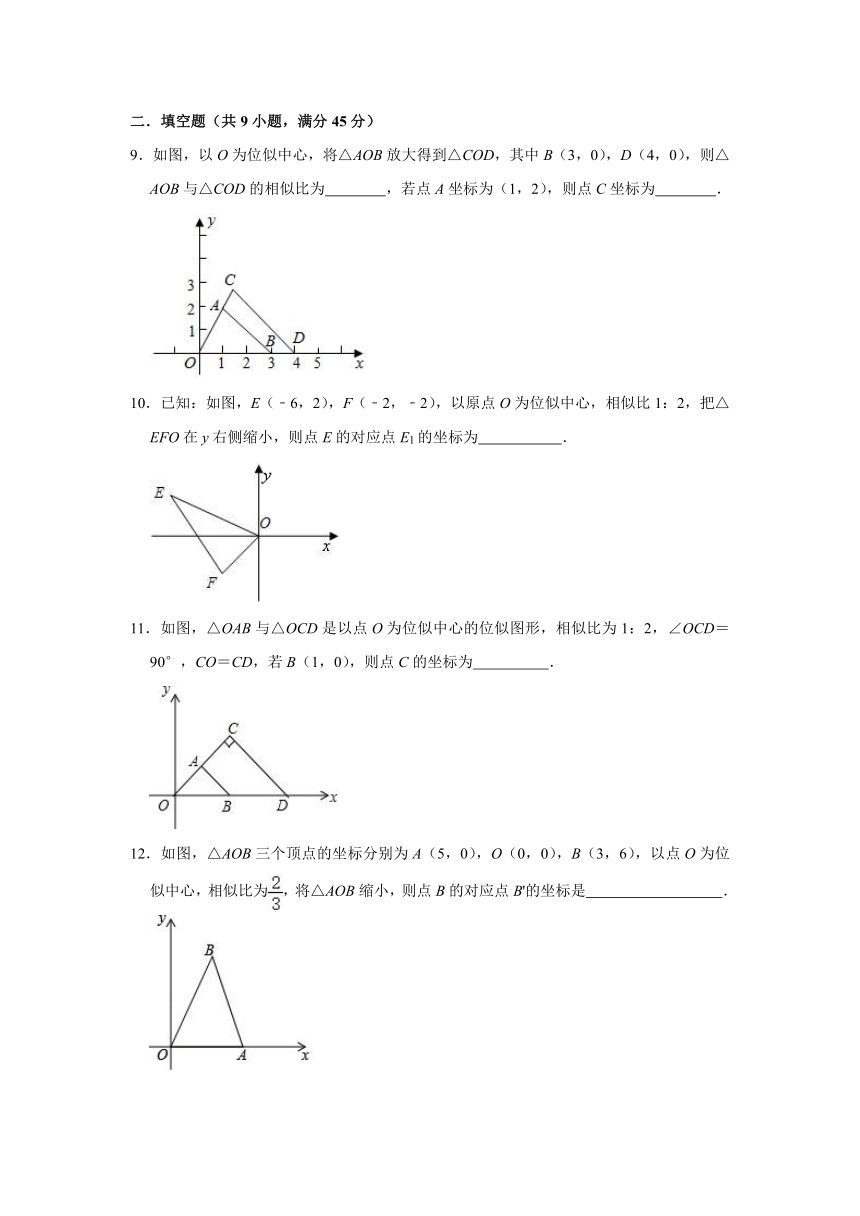
9.如图,以O为位似中心,将△AOB放大得到△COD,其中B(3,0),D(4,0),则△AOB与△COD的相似比为 ,若点A坐标为(1,2),则点C坐标为 .
10.已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为 .
11.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为 .
12.如图,△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以点O为位似中心,相似比为,将△AOB缩小,则点B的对应点B'的坐标是 .
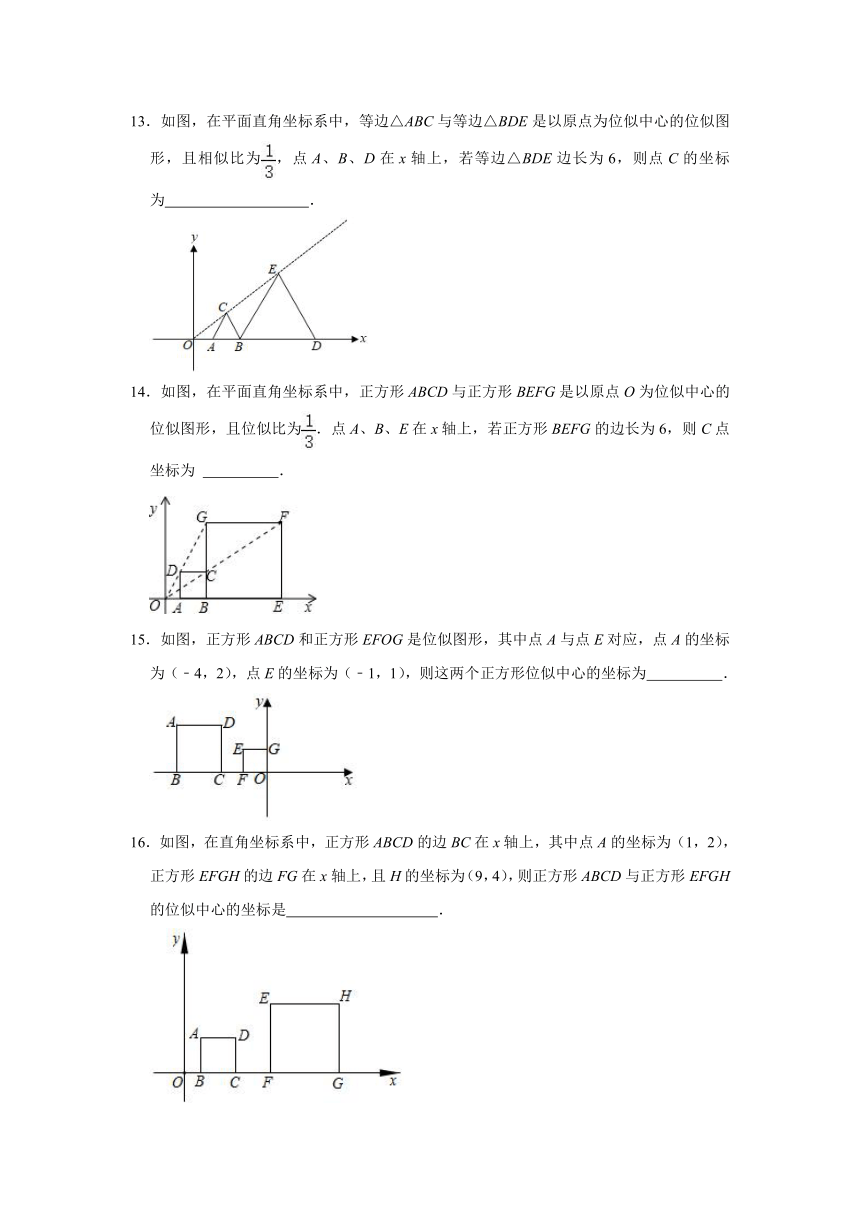
13.如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为,点A、B、D在x轴上,若等边△BDE边长为6,则点C的坐标为 .
14.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为 .
15.如图,正方形ABCD和正方形EFOG是位似图形,其中点A与点E对应,点A的坐标为(﹣4,2),点E的坐标为(﹣1,1),则这两个正方形位似中心的坐标为 .
16.如图,在直角坐标系中,正方形ABCD的边BC在x轴上,其中点A的坐标为(1,2),正方形EFGH的边FG在x轴上,且H的坐标为(9,4),则正方形ABCD与正方形EFGH的位似中心的坐标是 .
17.如图,平面直角坐标系中有正方形ABCD和正方形EFGH,若点A和点E的坐标分别为(﹣2,3),(1,﹣1),则两个正方形的位似中心的坐标是 .
三.解答题(共4小题,满分35分)
18.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,6).
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1,写出点C1的坐标.
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2,写出点B2的坐标.
19.如图,在平面直角坐标系中,△AOC的顶点坐标分别为A(2,2)、O(0,0)、C(,0),以原点O为位似中心.
(1)在第一象限内,相似比为,将△AOC缩小,不用画图,请直接写出缩小后的△A1OC1的两个顶点坐标:A1 ,C1
(2)相似比为2,将△AOC放大在第一象限画出放大后的△A2OC2,直接写出两个顶点的坐标:A2 ,C2 ;在第三象限画出放大后的△A3OC3,直接写出两个顶点的坐标:A3 ,C3
(3)相似比为k,将△AOC放大,若△AOC边上有任意一点P的坐标为(x,y),则放大后的图形上,点P的对应点Q的坐标为 .(用含k、x和y的式子表示)
(建议:先用铅笔画图,确定无误后用黑色水性笔画在答题卡上)
20.如图,△ABC各顶点坐标分别为:A(﹣4,4),B(﹣1,2),C(﹣5,1).
(1)画出△ABC关于原点O为中心对称的△A1B1C1;
(2)以O为位似中心,在x轴下方将△ABC放大为原来的2倍形成△A2B2C2;
(3)请写出下列各点坐标A2: ,B2: ,C2;: ;
(4)观察图形,若△A1B1C1中存在点P1(m,n),则在△A2B2C2中对应点P2的坐标为:
21.如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形?
(3)若AB=8,CD=4,DP=3,求AP的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵点A的坐标为(4,2),
∴OA==2,
∵△ABC与△A'B'C'位似,
∴△ABC∽△A'B'C',AC∥A′C′,
∴==,△AOC∽△A'OC',
∴==,
∴A'O=,
故选:B.
2.解:∵以原点O为位似中心,在第二象限内将△ABC各边扩大为原来的2倍,A(﹣2,3),
∴点A的对应点A′的坐标为(﹣2×2,3×2),即(﹣4,6),
绕原点O顺时针旋转90°得到△A′B′C′,则变换后的点A的对应点A′的坐标为(6,4),
故选:D.
3.解:∵以原点O为位似中心,把线段AB缩短为原来的,点B的坐标为(﹣4,3),
∴点D的坐标为(﹣4×,3×)或[﹣4×(﹣),3×(﹣)].即(﹣1,)或(1,﹣).
故选:D.
4.解:∵△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上,
即A点坐标为:(4,6),B点坐标为:(6,2),A′点坐标为:(2,3),B′点坐标为:(3,1),
∴线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为:().
故选:D.
5.解:∵△OCD与△OAB是以点O为位似中心的位似图形,D(3,0),B(9,0),
∴△OCD∽△OAB,相似比为1:3,
∵C(1,2),
∴点A的坐标为(3,6),
故选:B.
6.解:∵点A的坐标为(4,0),点C的坐标为(4,3),
∴OA=4,AC=3,
由勾股定理得:OC===5,
在Rt△OAC中,AP为△AOC中线,
∴OP=OC=,
以O为位似中心,把△AOP每条边扩大到原来的2倍,得到△A′OP′,
当△A′OP′在第三象限时,OP′=5,
则PP′=OP+OP′=+5=,
当△A′OP′在第一象限时,OP′=5,
则PP′=OP′﹣OP=5﹣=,
综上所述:PP′的长为或,
故选:D.
7.解:∵△ABC与△DEF是以坐标原点O为位似中心的位似图形,
∴△ABC∽△DEF,
∵A(﹣2,0),D(3,0),
∴OA=2,OD=3,
∴△ABC与△DEF的相似比为2:3,
∵BC=3,
∴EF=,
故选:C.
8.解:∵位似中心为坐标原点,作与△ABC的位似比为的位似图形△A'B'C',
而B的坐标为(﹣1,1),
∴B'的坐标为(﹣,)或(,﹣).
故选:C.
二.填空题(共9小题,满分45分)
9.解:由题意得,OB=3,OD=4,
∵将△AOB放大得到△COD,
∴△AOB∽△COD,相似比为3:4,
∵以O为位似中心,将△AOB放大得到△COD,点A坐标为(1,2),
∴点C坐标为(1×,2×),即(,),
故答案为:3:4;(,).
10.解:∵以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,E(﹣6,2),
∴点E的对应点E1的坐标为(6×,﹣2×),即(3,﹣1),
故答案为:(3,﹣1).
11.解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=,
∴A(,),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,1).
故答案为:(1,1).
12.解:如图,
∵△OAB∽△OA′B′,相似比为3:2,B(3,6),
∴B′(2,4),根据对称性可知,△OA″B″在第三象限时,B″(﹣2,﹣4),
∴满足条件的点B′的坐标为(2,4)或(﹣2,﹣4).
故答案为(2,4)或(﹣2,﹣4).
13.解:作CF⊥AB于F,
∵等边△ABC与等边△BDE是以原点为位似中心的位似图形,
∴BC∥DE,
∴△OBC∽△ODE,
∴=,
∵△ABC与△BDE的相似比为,等边△BDE边长为6,
∴==,
解得,BC=2,OB=3,
∴OA=1,
∵CA=CB,CF⊥AB,
∴AF=1,
由勾股定理得,CF==,
∴OF=OA+AF=2,
∴点C的坐标为(2,),
故答案为:(2,).
14.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为.
∴==,
而BE=EF=6,
∴==,
∴BC=2,OB=3,
∴C(3,2).
故答案为(3,2)
15.解:连接AE并延长交x轴于H,则点H为位似中心,
∵点A的坐标为(﹣4,2)点E的坐标为(﹣1,1),
∴OF=1,OB=4,EF=1,AB=2,
∵正方形ABCD和正方形EFOG是位似图形,
∴EF∥AB,
∴△HEF∽△HAB,
∴=,即=,
解得:OH=2,
∴点H的坐标为(2,0),
故答案为:(2,0).
16.解:连接HD并延长交x轴于点P,则点P为位似中心,
∵四边形ABCD为正方形,点A的坐标为(1,2),
∴点D的坐标为(3,2),
∵DC∥HG,
∴△PCD∽△PGH,
∴=,即=,
解得,OP=3,
∴正方形ABCD与正方形EFGH的位似中心的坐标是(﹣3,0),
连接CE、DF交于点P,
由题意得C(3,0),E(5,4),D(3,2),F(5,0),
求出直线DF解析式为:y=﹣x+5,直线CE解析式为:y=2x﹣6,
,
解得,,
直线DF,CE的交点P为(,),
所以正方形ABCD与正方形EFGH的位似中心的坐标是(,),
故答案为:(﹣3,0)或(,).
17.解:(1)当点A和E是对应顶点,B和F是对应顶点时,位似中心就是AE与BF的交点,
如图所示:连接AE,交x轴于点N,
点N即为两个正方形的位似中心,
∵点A和点E的坐标分别为(﹣2,3),(1,﹣1),
∴AB=3,EF=1,BF=1﹣(﹣2)=3,
∵AB∥EF,
∴△ABN∽△EFN,
∴=,
∴=,
解得:BN=,
∴ON=﹣2=,
∴两个正方形的位似中心的坐标是:(,0).
(2)当点A和G是对应顶点,C和E是对应顶点时,位似中心就是AG与CE的交点,
如图所示:连接AG,DF,BH,CE并延长交于点M,
设AG所在直线解析式为:y=kx+b,把A(﹣2,3),G(2,0)代入得:
故,
解得:,
故y=﹣x+;
设BH所在直线解析式为:y=mx+n,把B(﹣2,0),H(2,﹣1)代入得:
,
故y=﹣x﹣,
,
解得:,
故M(4,﹣),
综上所述:两个正方形的位似中心的坐标是:(,0)或(4,﹣).
故答案为:(,0)或(4,﹣).
三.解答题(共4小题,满分35分)
18.解:(1)如图,△A1B1C1为所求作的三角形,C1(3,3).
(2)如图所示,则△A2B2C2为所求作的三角形,B2(2,8).
19.解:(1)A1(1,1),C1(,0);
故答案为:(1,1),(,0);
(2)如图所示:A2(4,4),C2(5,0);A3(﹣4,﹣4),C3(﹣5,0);
故答案为:(4,4),(5,0),(﹣4,﹣4),(﹣5,0);
(3)相似比为k,将△AOC放大,若△AOC边上有任意一点P的坐标为(x,y),
则放大后的图形上,点P的对应点Q的坐标为:(kx,ky)或(﹣kx,﹣ky).
故答案为:(kx,ky)或(﹣kx,﹣ky).
20.解:(1)∵A(﹣4,4),B(﹣1,2),C(﹣5,1),△ABC与△A1B1C1关于原点O中心对称;
∴A1(4,﹣4),B1(1,﹣2),C1(5,﹣1),连接各点即可.
(2)∵以O为位似中心,在x轴下方将△ABC放大为原来的2倍形成△A2B2C2;
∴A2(8,﹣8),B2(2,﹣4),C2(10,﹣2),连接即可;
(3)故答案为:(8,﹣8),(2,﹣4),(10,﹣2);
(4)故答案为:(2m,2n).
21.(1)证明∵∠DAP=∠CBP,∠DPA=∠CPB,
∴△ADP∽△BCP;
(2)解:△ADP与△BCP不是位似图形,
因为它们的对应点的连线不平行;
(3)解:∵△ADP∽△BCP,
∴=,又∠APB=∠DPC,
∴△APB∽△DPC,
∴=,即=,
解得,AP=6.
一.选择题(共8小题,满分40分)
1.如图,△ABC与△A'B'C'位似,点O是它们的位似中心,其中BC=2B'C',若点A的坐标为(4,2),则A'O的长度为( )
A. B. C. D.
2.如图,在平面直角坐标系中,已知△ABC点A(﹣2,3),C(﹣1,2),以原点O为位似中心,在第二象限内将△ABC各边扩大为原来的2倍,再绕原点O顺时针旋转90°得到△A′B′C′,则变换后的点A的对应点A′的坐标为( )
A.(2,6) B.(4,2) C.(3,2) D.(6,4)
3.已知点A(0,3),B(﹣4,3),以原点O为位似中心,把线段AB缩短为原来的,其中点C与点A对应,点D与点B对应.则点D的坐标为( )
A.(﹣1,) B.(1,﹣)
C.(,﹣1)或(﹣,1) D.(﹣1,)或(1,﹣)
4.如图,△ABO缩小后变为△A'B'O,其中A、B的对应点分别为A'、B',点A、B、A'、B'均在格点上,若线段AB上有点P(m,n),则点P在A'B'上的对应点P'的坐标为( )
A.(,n) B.(m,n) C.(m,) D.()
5.如图,已知△OCD与△OAB是以点O为位似中心的位似图形,若C(1,2),D(3,0),B(9,0),则点A的坐标为( )
A.(2,4) B.(3,6) C.(3,5) D.(4,5)
6.如图,△AOC中三个顶点的坐标分别为(4,0)、(0,0)、(4,3),AP为△AOC中线,以O为位似中心,把△AOP每条边扩大到原来的2倍,得到△A′OP′,则PP′的长为( )
A. B. C.或 D.或
7.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且BC=3,则线段EF的长度为( )
A.2 B.4 C. D.6
8.如图,在直角坐标系中,△ABC的顶点B的坐标为(﹣1,1),现以坐标原点O为位似中心,作与△ABC的位似比为的位似图形△A'B'C',则B'的坐标为( )
A. B.
C.或 D.或
二.填空题(共9小题,满分45分)
9.如图,以O为位似中心,将△AOB放大得到△COD,其中B(3,0),D(4,0),则△AOB与△COD的相似比为 ,若点A坐标为(1,2),则点C坐标为 .
10.已知:如图,E(﹣6,2),F(﹣2,﹣2),以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,则点E的对应点E1的坐标为 .
11.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为 .
12.如图,△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以点O为位似中心,相似比为,将△AOB缩小,则点B的对应点B'的坐标是 .
13.如图,在平面直角坐标系中,等边△ABC与等边△BDE是以原点为位似中心的位似图形,且相似比为,点A、B、D在x轴上,若等边△BDE边长为6,则点C的坐标为 .
14.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为 .
15.如图,正方形ABCD和正方形EFOG是位似图形,其中点A与点E对应,点A的坐标为(﹣4,2),点E的坐标为(﹣1,1),则这两个正方形位似中心的坐标为 .
16.如图,在直角坐标系中,正方形ABCD的边BC在x轴上,其中点A的坐标为(1,2),正方形EFGH的边FG在x轴上,且H的坐标为(9,4),则正方形ABCD与正方形EFGH的位似中心的坐标是 .
17.如图,平面直角坐标系中有正方形ABCD和正方形EFGH,若点A和点E的坐标分别为(﹣2,3),(1,﹣1),则两个正方形的位似中心的坐标是 .
三.解答题(共4小题,满分35分)
18.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,6).
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1,写出点C1的坐标.
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2,写出点B2的坐标.
19.如图,在平面直角坐标系中,△AOC的顶点坐标分别为A(2,2)、O(0,0)、C(,0),以原点O为位似中心.
(1)在第一象限内,相似比为,将△AOC缩小,不用画图,请直接写出缩小后的△A1OC1的两个顶点坐标:A1 ,C1
(2)相似比为2,将△AOC放大在第一象限画出放大后的△A2OC2,直接写出两个顶点的坐标:A2 ,C2 ;在第三象限画出放大后的△A3OC3,直接写出两个顶点的坐标:A3 ,C3
(3)相似比为k,将△AOC放大,若△AOC边上有任意一点P的坐标为(x,y),则放大后的图形上,点P的对应点Q的坐标为 .(用含k、x和y的式子表示)
(建议:先用铅笔画图,确定无误后用黑色水性笔画在答题卡上)
20.如图,△ABC各顶点坐标分别为:A(﹣4,4),B(﹣1,2),C(﹣5,1).
(1)画出△ABC关于原点O为中心对称的△A1B1C1;
(2)以O为位似中心,在x轴下方将△ABC放大为原来的2倍形成△A2B2C2;
(3)请写出下列各点坐标A2: ,B2: ,C2;: ;
(4)观察图形,若△A1B1C1中存在点P1(m,n),则在△A2B2C2中对应点P2的坐标为:
21.如图,BD,AC相交于点P,连接AB,BC,CD,DA,∠DAP=∠CBP.
(1)求证:△ADP∽△BCP;
(2)直接回答△ADP与△BCP是不是位似图形?
(3)若AB=8,CD=4,DP=3,求AP的长.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵点A的坐标为(4,2),
∴OA==2,
∵△ABC与△A'B'C'位似,
∴△ABC∽△A'B'C',AC∥A′C′,
∴==,△AOC∽△A'OC',
∴==,
∴A'O=,
故选:B.
2.解:∵以原点O为位似中心,在第二象限内将△ABC各边扩大为原来的2倍,A(﹣2,3),
∴点A的对应点A′的坐标为(﹣2×2,3×2),即(﹣4,6),
绕原点O顺时针旋转90°得到△A′B′C′,则变换后的点A的对应点A′的坐标为(6,4),
故选:D.
3.解:∵以原点O为位似中心,把线段AB缩短为原来的,点B的坐标为(﹣4,3),
∴点D的坐标为(﹣4×,3×)或[﹣4×(﹣),3×(﹣)].即(﹣1,)或(1,﹣).
故选:D.
4.解:∵△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上,
即A点坐标为:(4,6),B点坐标为:(6,2),A′点坐标为:(2,3),B′点坐标为:(3,1),
∴线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为:().
故选:D.
5.解:∵△OCD与△OAB是以点O为位似中心的位似图形,D(3,0),B(9,0),
∴△OCD∽△OAB,相似比为1:3,
∵C(1,2),
∴点A的坐标为(3,6),
故选:B.
6.解:∵点A的坐标为(4,0),点C的坐标为(4,3),
∴OA=4,AC=3,
由勾股定理得:OC===5,
在Rt△OAC中,AP为△AOC中线,
∴OP=OC=,
以O为位似中心,把△AOP每条边扩大到原来的2倍,得到△A′OP′,
当△A′OP′在第三象限时,OP′=5,
则PP′=OP+OP′=+5=,
当△A′OP′在第一象限时,OP′=5,
则PP′=OP′﹣OP=5﹣=,
综上所述:PP′的长为或,
故选:D.
7.解:∵△ABC与△DEF是以坐标原点O为位似中心的位似图形,
∴△ABC∽△DEF,
∵A(﹣2,0),D(3,0),
∴OA=2,OD=3,
∴△ABC与△DEF的相似比为2:3,
∵BC=3,
∴EF=,
故选:C.
8.解:∵位似中心为坐标原点,作与△ABC的位似比为的位似图形△A'B'C',
而B的坐标为(﹣1,1),
∴B'的坐标为(﹣,)或(,﹣).
故选:C.
二.填空题(共9小题,满分45分)
9.解:由题意得,OB=3,OD=4,
∵将△AOB放大得到△COD,
∴△AOB∽△COD,相似比为3:4,
∵以O为位似中心,将△AOB放大得到△COD,点A坐标为(1,2),
∴点C坐标为(1×,2×),即(,),
故答案为:3:4;(,).
10.解:∵以原点O为位似中心,相似比1:2,把△EFO在y右侧缩小,E(﹣6,2),
∴点E的对应点E1的坐标为(6×,﹣2×),即(3,﹣1),
故答案为:(3,﹣1).
11.解:∵∠OAB=∠OCD=90°,AO=AB,CO=CD,等腰Rt△OAB与等腰Rt△OCD是位似图形,点B的坐标为(1,0),
∴BO=1,则AO=AB=,
∴A(,),
∵等腰Rt△OAB与等腰Rt△OCD是位似图形,O为位似中心,相似比为1:2,
∴点C的坐标为:(1,1).
故答案为:(1,1).
12.解:如图,
∵△OAB∽△OA′B′,相似比为3:2,B(3,6),
∴B′(2,4),根据对称性可知,△OA″B″在第三象限时,B″(﹣2,﹣4),
∴满足条件的点B′的坐标为(2,4)或(﹣2,﹣4).
故答案为(2,4)或(﹣2,﹣4).
13.解:作CF⊥AB于F,
∵等边△ABC与等边△BDE是以原点为位似中心的位似图形,
∴BC∥DE,
∴△OBC∽△ODE,
∴=,
∵△ABC与△BDE的相似比为,等边△BDE边长为6,
∴==,
解得,BC=2,OB=3,
∴OA=1,
∵CA=CB,CF⊥AB,
∴AF=1,
由勾股定理得,CF==,
∴OF=OA+AF=2,
∴点C的坐标为(2,),
故答案为:(2,).
14.解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为.
∴==,
而BE=EF=6,
∴==,
∴BC=2,OB=3,
∴C(3,2).
故答案为(3,2)
15.解:连接AE并延长交x轴于H,则点H为位似中心,
∵点A的坐标为(﹣4,2)点E的坐标为(﹣1,1),
∴OF=1,OB=4,EF=1,AB=2,
∵正方形ABCD和正方形EFOG是位似图形,
∴EF∥AB,
∴△HEF∽△HAB,
∴=,即=,
解得:OH=2,
∴点H的坐标为(2,0),
故答案为:(2,0).
16.解:连接HD并延长交x轴于点P,则点P为位似中心,
∵四边形ABCD为正方形,点A的坐标为(1,2),
∴点D的坐标为(3,2),
∵DC∥HG,
∴△PCD∽△PGH,
∴=,即=,
解得,OP=3,
∴正方形ABCD与正方形EFGH的位似中心的坐标是(﹣3,0),
连接CE、DF交于点P,
由题意得C(3,0),E(5,4),D(3,2),F(5,0),
求出直线DF解析式为:y=﹣x+5,直线CE解析式为:y=2x﹣6,
,
解得,,
直线DF,CE的交点P为(,),
所以正方形ABCD与正方形EFGH的位似中心的坐标是(,),
故答案为:(﹣3,0)或(,).
17.解:(1)当点A和E是对应顶点,B和F是对应顶点时,位似中心就是AE与BF的交点,
如图所示:连接AE,交x轴于点N,
点N即为两个正方形的位似中心,
∵点A和点E的坐标分别为(﹣2,3),(1,﹣1),
∴AB=3,EF=1,BF=1﹣(﹣2)=3,
∵AB∥EF,
∴△ABN∽△EFN,
∴=,
∴=,
解得:BN=,
∴ON=﹣2=,
∴两个正方形的位似中心的坐标是:(,0).
(2)当点A和G是对应顶点,C和E是对应顶点时,位似中心就是AG与CE的交点,
如图所示:连接AG,DF,BH,CE并延长交于点M,
设AG所在直线解析式为:y=kx+b,把A(﹣2,3),G(2,0)代入得:
故,
解得:,
故y=﹣x+;
设BH所在直线解析式为:y=mx+n,把B(﹣2,0),H(2,﹣1)代入得:
,
故y=﹣x﹣,
,
解得:,
故M(4,﹣),
综上所述:两个正方形的位似中心的坐标是:(,0)或(4,﹣).
故答案为:(,0)或(4,﹣).
三.解答题(共4小题,满分35分)
18.解:(1)如图,△A1B1C1为所求作的三角形,C1(3,3).
(2)如图所示,则△A2B2C2为所求作的三角形,B2(2,8).
19.解:(1)A1(1,1),C1(,0);
故答案为:(1,1),(,0);
(2)如图所示:A2(4,4),C2(5,0);A3(﹣4,﹣4),C3(﹣5,0);
故答案为:(4,4),(5,0),(﹣4,﹣4),(﹣5,0);
(3)相似比为k,将△AOC放大,若△AOC边上有任意一点P的坐标为(x,y),
则放大后的图形上,点P的对应点Q的坐标为:(kx,ky)或(﹣kx,﹣ky).
故答案为:(kx,ky)或(﹣kx,﹣ky).
20.解:(1)∵A(﹣4,4),B(﹣1,2),C(﹣5,1),△ABC与△A1B1C1关于原点O中心对称;
∴A1(4,﹣4),B1(1,﹣2),C1(5,﹣1),连接各点即可.
(2)∵以O为位似中心,在x轴下方将△ABC放大为原来的2倍形成△A2B2C2;
∴A2(8,﹣8),B2(2,﹣4),C2(10,﹣2),连接即可;
(3)故答案为:(8,﹣8),(2,﹣4),(10,﹣2);
(4)故答案为:(2m,2n).
21.(1)证明∵∠DAP=∠CBP,∠DPA=∠CPB,
∴△ADP∽△BCP;
(2)解:△ADP与△BCP不是位似图形,
因为它们的对应点的连线不平行;
(3)解:∵△ADP∽△BCP,
∴=,又∠APB=∠DPC,
∴△APB∽△DPC,
∴=,即=,
解得,AP=6.
