北师大版八年级数学上册 7.5 三角形全等(1)(共33张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 7.5 三角形全等(1)(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 10:51:33 | ||
图片预览





文档简介
(共33张PPT)
17.1勾股定理
复习提问
1、任意三角形三边满足怎样的关系?
2、对于等腰三角形,三边之间存在怎样的特殊关系?等边三角形呢?
3、对于直角三角形,三边之间存在怎样的特殊关系?
2002年在北京召开了第24届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”,这就是本届大会会徽的图案。
这个图案就是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”
探索勾股定理
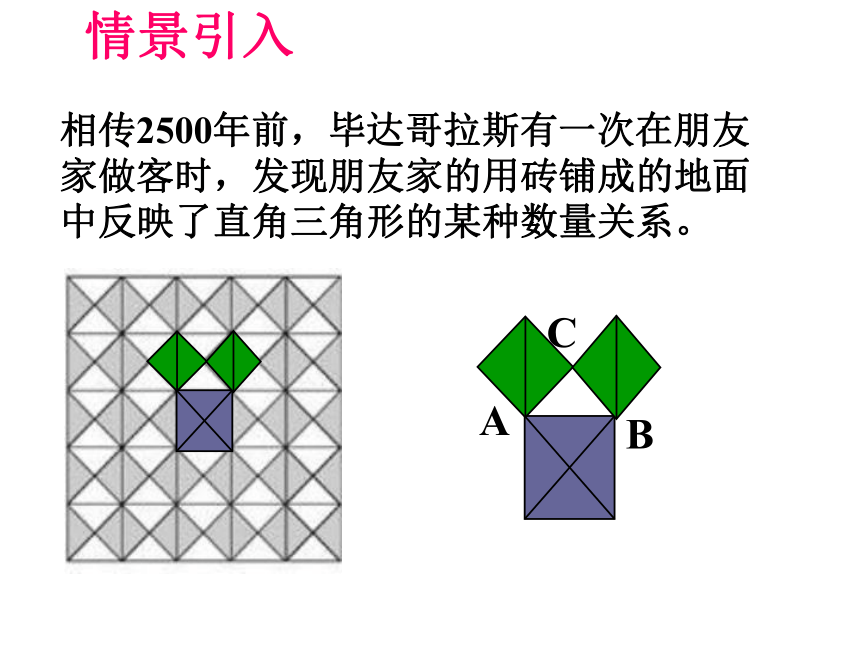
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形的某种数量关系。
C
B
A
情景引入
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
(1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
你是怎样得到C的面积的?与同伴交流交流。
1
2
3
(2)(3)
探究活动一:
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
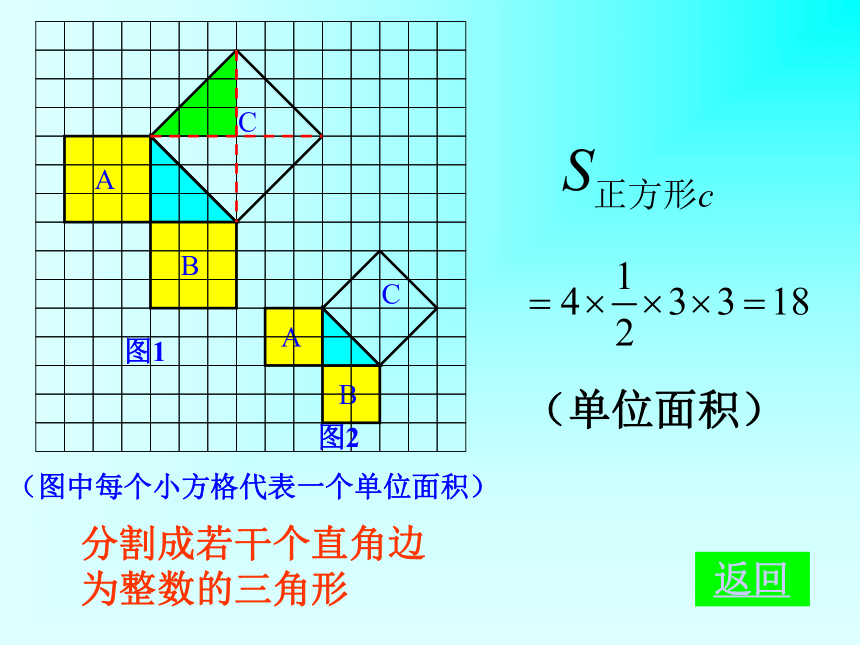
分割成若干个直角边为整数的三角形
(单位面积)
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
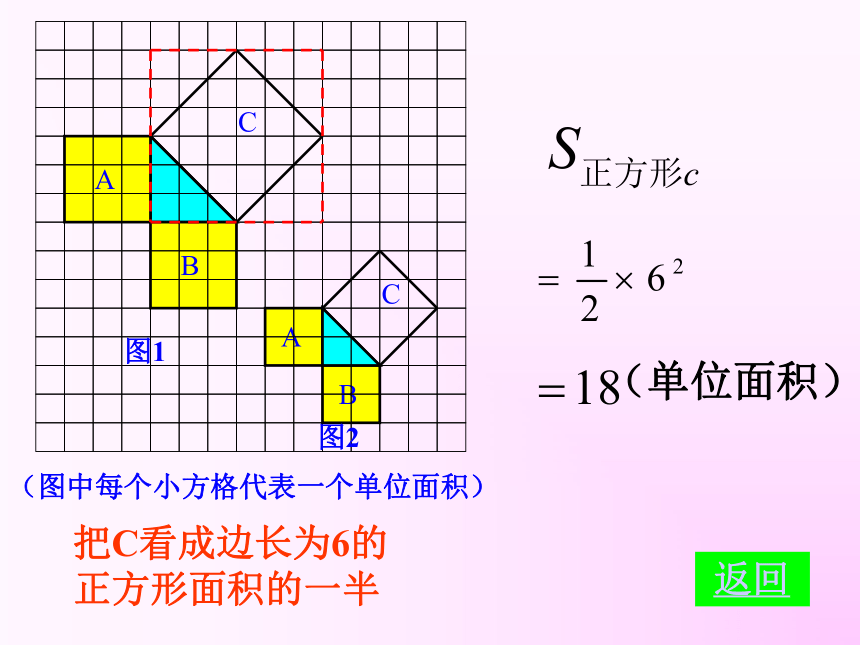
(单位面积)
把C看成边长为6的正方形面积的一半
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图 1
图 2
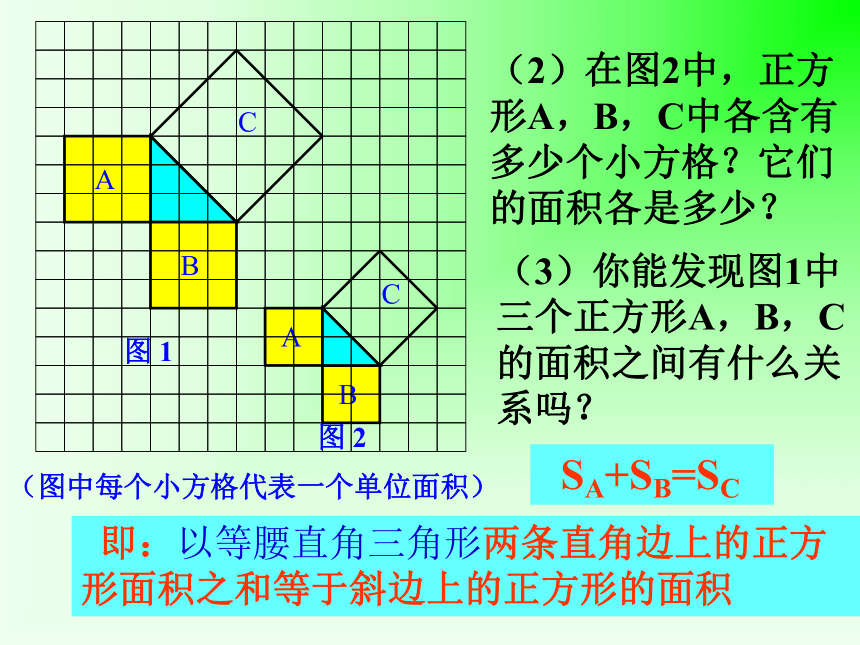
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:以等腰直角三角形两条直角边上的正方形面积之和等于斜边上的正方形的面积
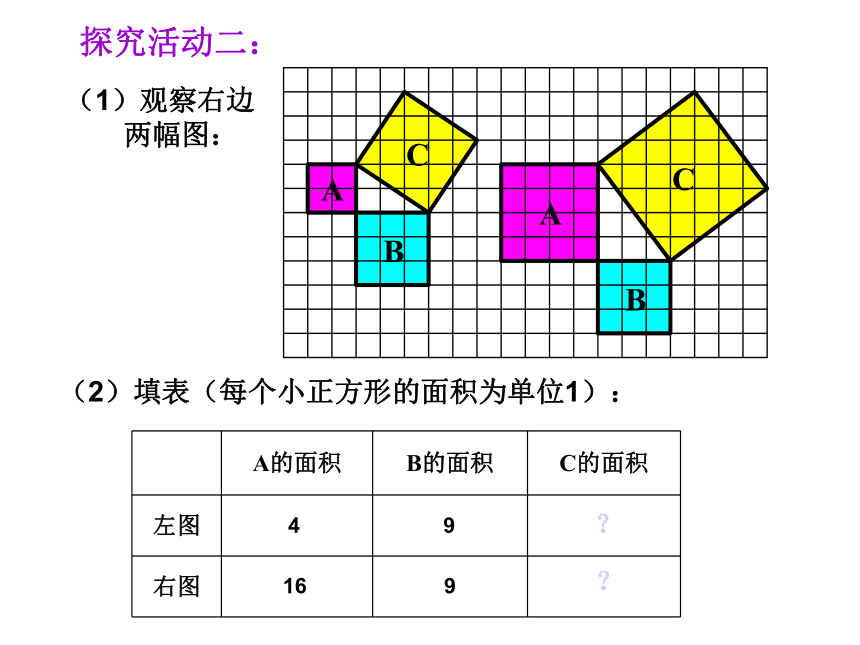
探究活动二:
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
?
?
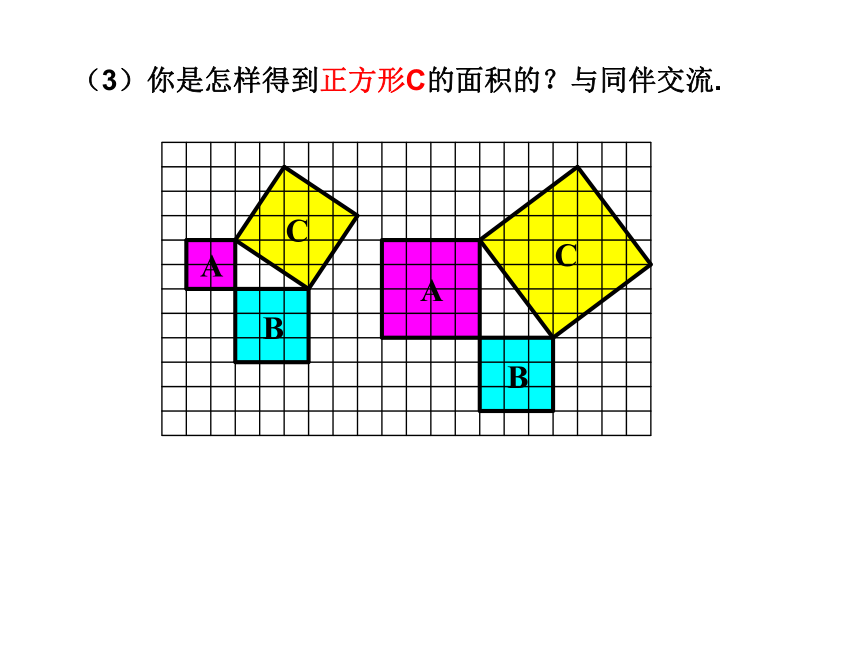
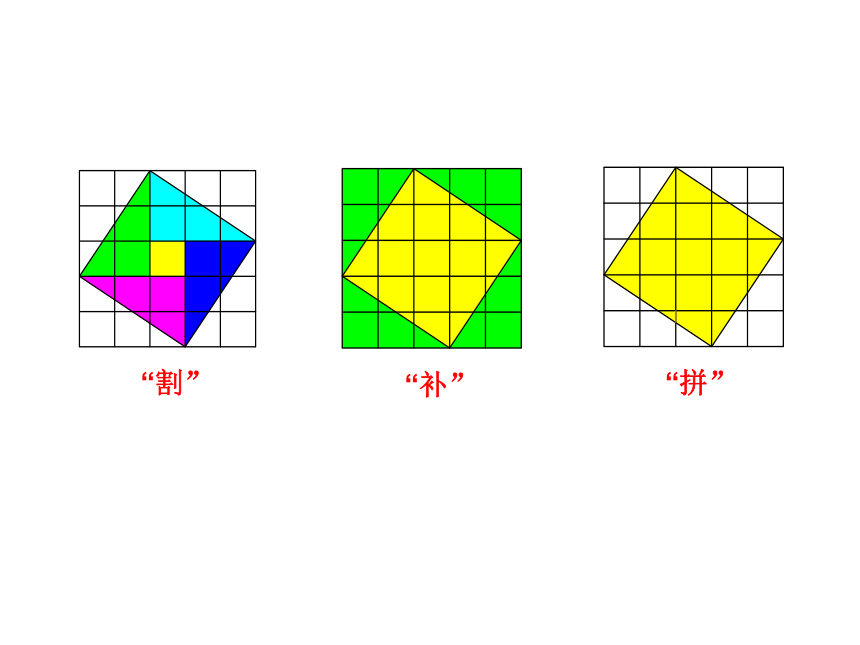
(3)你是怎样得到正方形C的面积的?与同伴交流.
“割”
“补”
“拼”
(4)分析填表数据,你发现了什么?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
议一议:
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么
关系吗?
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
表示为:Rt△ABC中,∠C=90°
则
议一议:判断下列说法是否正确,并说明理由:
(1)在△ABC中,若a=3,b=4,则c=5
(2)在Rt△ABC中,如果a=3,b=4,则c=5.
(3)在Rt△ABC中,∠C=90° , 如果a=3,b=4,则c=5.
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
探究活动
分成四人小组,每个小组课前准备好4个全等的直角三角形和以直角三角形各边为边长的3个正方形(如右图).
运用这些材料(不一定全用),你能另外拼出一些正方形吗?试试看,你能拼几种.
图1
图3
图2
方法一:
而
所以
即
,
,
.
.
因为
,
方法二:
,
化简得:
方法三:
,
化简得:
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
做一做
625
576
144
169
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
C
A.8 米 B.9 米 C.10米 D.14米
1、如图,一个长8 米,宽6 米的草地,需在相对角的顶点间加一条小路,则小路的长为 ( )
8m
6m
别踩我,我怕疼!
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
某楼房在20米高处的楼层失火,消防员取来25米长的云梯救火,已知梯子的底部离墙的距离是15米。问消防队员能否进入该楼层灭火?
已知两直角边求斜边
A
B
C
15
20
我国古代两种证法:
1、公元3世纪我国汉代数学家赵爽在为《周髀算经》作注时给出的“弦图”:
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的。每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图。2002年的国际数学家大会将此图作为大会会徽.
2、我国数学家刘徽在他的《九章算术注》中给出的“青朱出入图” :
证法四:(伽菲尔德证法1876年)
A
B
C
D
E
如图,Rt△ABE≌Rt△ECD,
可知∠AED=90°;
梯形ABCD的面积=
梯形ABCD的面积=
∴
∴
证法五:(欧几里得证法公元前3世纪)
“新娘的轿椅”或“修士的头巾”
如图,Rt△ ABC中,∠ACB=90°,四边形ACHK、BCGF、ABED都是正方形,CN⊥DE,连接BK、CD。
AK=AC
AB=AD
∠KAB=∠CAD
△KAB≌△CAD
S 正方形KACH = S 四边形ADNM
同理:S 正方形BCGF = S 四边形BENM
S 正方形KACH + S 正方形BCGF = S 四边形ADNM + S 四边形BENM
S △KAB = S △CAD
∴
S 正方形KACH + S 正方形BCGF = S 四边形ADEB
17.1勾股定理
复习提问
1、任意三角形三边满足怎样的关系?
2、对于等腰三角形,三边之间存在怎样的特殊关系?等边三角形呢?
3、对于直角三角形,三边之间存在怎样的特殊关系?
2002年在北京召开了第24届国际数学家大会,它是最高水平的全球性数学科学学术会议,被誉为数学界的“奥运会”,这就是本届大会会徽的图案。
这个图案就是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”
探索勾股定理
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形的某种数量关系。
C
B
A
情景引入
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
(1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
9
9
9
18
你是怎样得到C的面积的?与同伴交流交流。
1
2
3
(2)(3)
探究活动一:
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
分割成若干个直角边为整数的三角形
(单位面积)
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
(单位面积)
把C看成边长为6的正方形面积的一半
返回
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图 1
图 2
(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:以等腰直角三角形两条直角边上的正方形面积之和等于斜边上的正方形的面积
探究活动二:
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积 B的面积 C的面积
左图
右图
4 9
16 9
?
?
(3)你是怎样得到正方形C的面积的?与同伴交流.
“割”
“补”
“拼”
(4)分析填表数据,你发现了什么?
A的面积 B的面积 C的面积
左图 4 9 13
右图 16 9 25
结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
议一议:
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么
关系吗?
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
表示为:Rt△ABC中,∠C=90°
则
议一议:判断下列说法是否正确,并说明理由:
(1)在△ABC中,若a=3,b=4,则c=5
(2)在Rt△ABC中,如果a=3,b=4,则c=5.
(3)在Rt△ABC中,∠C=90° , 如果a=3,b=4,则c=5.
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
探究活动
分成四人小组,每个小组课前准备好4个全等的直角三角形和以直角三角形各边为边长的3个正方形(如右图).
运用这些材料(不一定全用),你能另外拼出一些正方形吗?试试看,你能拼几种.
图1
图3
图2
方法一:
而
所以
即
,
,
.
.
因为
,
方法二:
,
化简得:
方法三:
,
化简得:
1.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
做一做
625
576
144
169
比一比看看谁算得快!
2.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
8
x
17
16
20
x
12
5
x
做一做
C
A.8 米 B.9 米 C.10米 D.14米
1、如图,一个长8 米,宽6 米的草地,需在相对角的顶点间加一条小路,则小路的长为 ( )
8m
6m
别踩我,我怕疼!
2、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A
B
C
A.50米 B.120米 C.100米 D.130米
130
120
A
某楼房在20米高处的楼层失火,消防员取来25米长的云梯救火,已知梯子的底部离墙的距离是15米。问消防队员能否进入该楼层灭火?
已知两直角边求斜边
A
B
C
15
20
我国古代两种证法:
1、公元3世纪我国汉代数学家赵爽在为《周髀算经》作注时给出的“弦图”:
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的。每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图。2002年的国际数学家大会将此图作为大会会徽.
2、我国数学家刘徽在他的《九章算术注》中给出的“青朱出入图” :
证法四:(伽菲尔德证法1876年)
A
B
C
D
E
如图,Rt△ABE≌Rt△ECD,
可知∠AED=90°;
梯形ABCD的面积=
梯形ABCD的面积=
∴
∴
证法五:(欧几里得证法公元前3世纪)
“新娘的轿椅”或“修士的头巾”
如图,Rt△ ABC中,∠ACB=90°,四边形ACHK、BCGF、ABED都是正方形,CN⊥DE,连接BK、CD。
AK=AC
AB=AD
∠KAB=∠CAD
△KAB≌△CAD
S 正方形KACH = S 四边形ADNM
同理:S 正方形BCGF = S 四边形BENM
S 正方形KACH + S 正方形BCGF = S 四边形ADNM + S 四边形BENM
S △KAB = S △CAD
∴
S 正方形KACH + S 正方形BCGF = S 四边形ADEB
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
