2021—2022学年青岛版数学八年级上册1.2 怎样判定三角形全等 同步练习卷(Word版含答案)
文档属性
| 名称 | 2021—2022学年青岛版数学八年级上册1.2 怎样判定三角形全等 同步练习卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 104.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 09:21:17 | ||
图片预览

文档简介
2021年青岛版数学八年级上册
1.2《怎样判定三角形全等》同步练习卷
一、选择题
1.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
2.在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,若证△ABC≌△A′B′C′还要从下列条件中补选一个,错误的选法是( )
A.∠B=∠B′ B.∠C=∠C′ C.BC=B′C′ D.AC=A′C′
3.下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
4.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的有( )
A.∠BAD=∠CAE B.△ABD≌△ACE C.AB=BC D.BD=CE
5.如图,AD,BC相交于点O,OA=OD,OB=OC.下列结论正确的是( )
A.△AOB≌△DOC B.△ABO≌△DOC C.∠A=∠C D.∠B=∠D
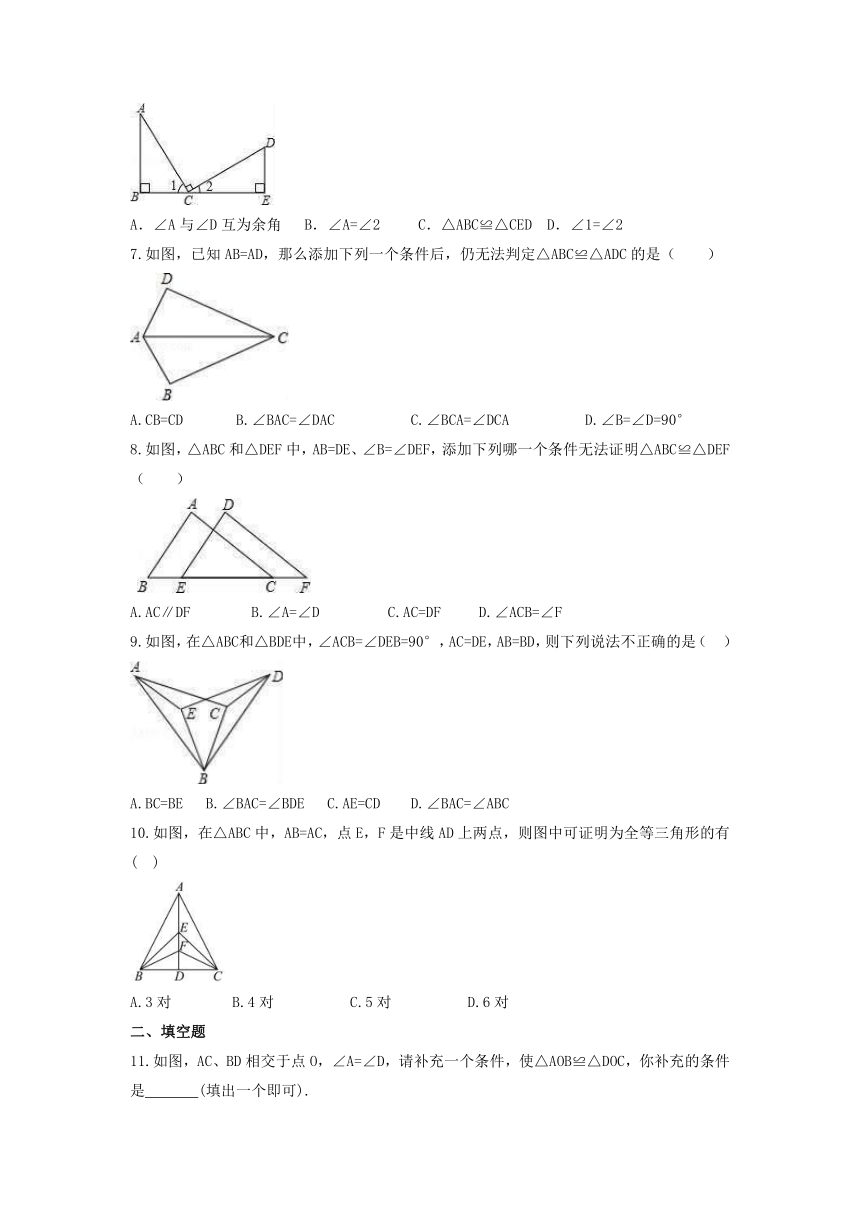
6.如图,已知AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
A.∠A与∠D互为余角 B.∠A=∠2 C.△ABC≌△CED D.∠1=∠2
7.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
8.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F
9.如图,在△ABC和△BDE中,∠ACB=∠DEB=90°,AC=DE,AB=BD,则下列说法不正确的是( )
A.BC=BE B.∠BAC=∠BDE C.AE=CD D.∠BAC=∠ABC
10.如图,在△ABC中,AB=AC,点E,F是中线AD上两点,则图中可证明为全等三角形的有( )
A.3对 B.4对 C.5对 D.6对
二、填空题
11.如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是 (填出一个即可).
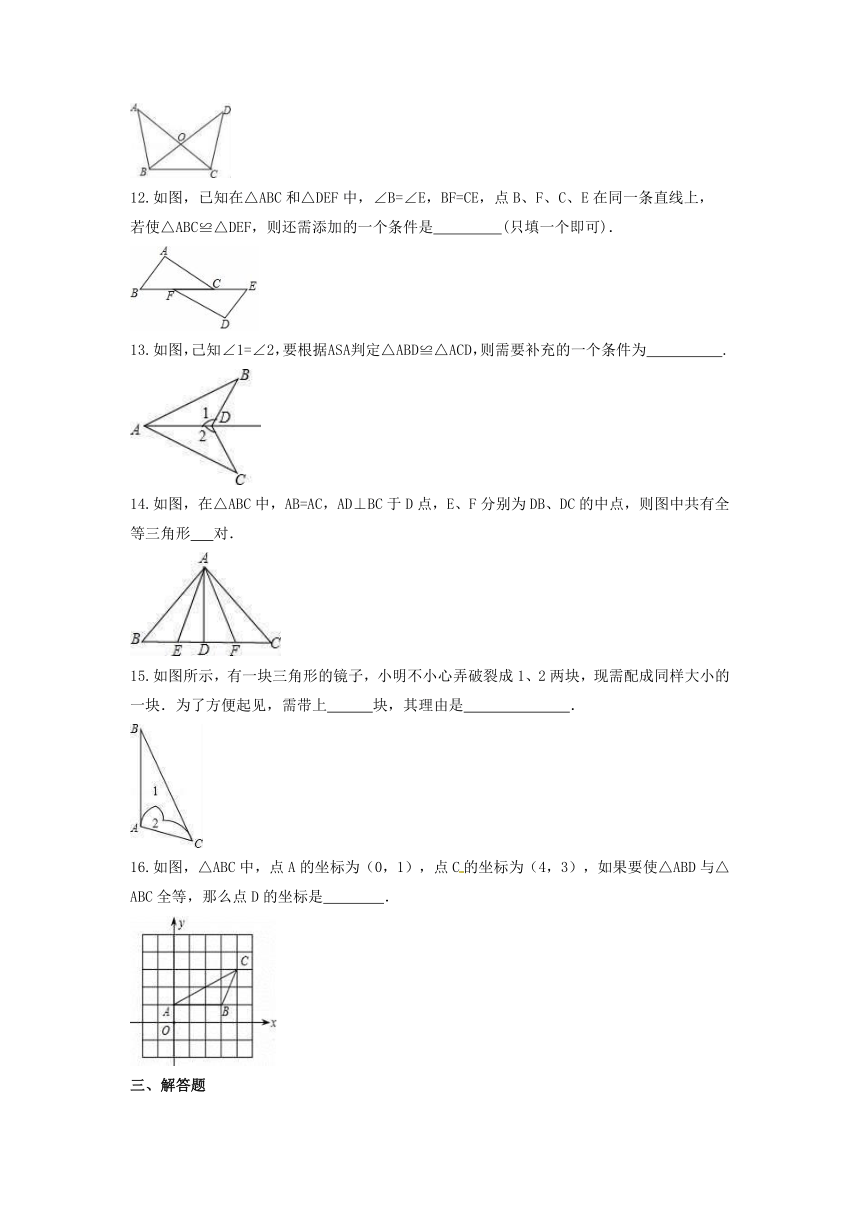
12.如图,已知在△ABC和△DEF中,∠B=∠E,BF=CE,点B、F、C、E在同一条直线上,
若使△ABC≌△DEF,则还需添加的一个条件是 (只填一个即可).
13.如图,己知∠1=∠2,要根据ASA判定△ABD≌△ACD,则需要补充的一个条件为 .
14.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.
15.如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上 块,其理由是 .
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 .
三、解答题
17.如图,A、B两个建筑分别位于河的两岸,要测得它们之间距离,可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E、A、C在同一条直线上,则DE长就是A、B之间的距离,请你说明道理.
18.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD,求证:AE=FB.
( http: / / www." \o "中国教育出版网 )
19.课间,小明拿着老师的等腰直角三角尺玩,不小心掉到两堆砖块之间,如图所示.
(1)求证:△ADC≌△CEB;
(2)已知DE=35cm,请你帮小明求出砖块的厚度a的大小(每块砖的厚度相同).
20.如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.
参考答案
1.C
2.C
3.B
4.C
5.A
6.D.
7.C.
8.C.
9.D;
10.D;
11.答案为:AB=CD(答案不唯一).
12.答案为:AB=DE.
13.答案为:AAS.
14.答案为:4
15.答案为:第1,利用SAS得出全等三角形,即可配成与原来同样大小的一块.
16.答案为:(4,﹣1)或(﹣1,3)或(﹣1,﹣1)
17.解:∵DE∥AB
∴∠A=∠E
在ABC和EDC中
∴△ABC≌△EDC (AAS)
∴AB=DE
即DE长就是A、B之间距离
18.证明:∵CE∥DF
∴∠ECA=∠FDB,
在△ECA和△FDB中
( http: / / www." \o "中国教育出版网 ),
∴△ECA≌△FDB,
∴AE=FB.
19.(1)证明:由题意得:
AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
∠ADC=∠CEB,∠DAC=∠BCE,AC=BC
∴△ADC≌△CEB(AAS);
(2)解:由题意得:∵一块墙砖的厚度为a,
∴AD=4a,BE=3a,
由(1)得:△ADC≌△CEB,
∴DC=BE=3a,AD=CE=4a,
∴DC+CE=BE+AD=7a=42,
∴a=6,
答:砌墙砖块的厚度a为6cm.
20.证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC,
∵AE=AD,
∴AB﹣AD=AC﹣AE,即BD=CE,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),
∴DF=EF.
1.2《怎样判定三角形全等》同步练习卷
一、选择题
1.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
2.在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,若证△ABC≌△A′B′C′还要从下列条件中补选一个,错误的选法是( )
A.∠B=∠B′ B.∠C=∠C′ C.BC=B′C′ D.AC=A′C′
3.下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
4.如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的有( )
A.∠BAD=∠CAE B.△ABD≌△ACE C.AB=BC D.BD=CE
5.如图,AD,BC相交于点O,OA=OD,OB=OC.下列结论正确的是( )
A.△AOB≌△DOC B.△ABO≌△DOC C.∠A=∠C D.∠B=∠D
6.如图,已知AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
A.∠A与∠D互为余角 B.∠A=∠2 C.△ABC≌△CED D.∠1=∠2
7.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
8.如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F
9.如图,在△ABC和△BDE中,∠ACB=∠DEB=90°,AC=DE,AB=BD,则下列说法不正确的是( )
A.BC=BE B.∠BAC=∠BDE C.AE=CD D.∠BAC=∠ABC
10.如图,在△ABC中,AB=AC,点E,F是中线AD上两点,则图中可证明为全等三角形的有( )
A.3对 B.4对 C.5对 D.6对
二、填空题
11.如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是 (填出一个即可).
12.如图,已知在△ABC和△DEF中,∠B=∠E,BF=CE,点B、F、C、E在同一条直线上,
若使△ABC≌△DEF,则还需添加的一个条件是 (只填一个即可).
13.如图,己知∠1=∠2,要根据ASA判定△ABD≌△ACD,则需要补充的一个条件为 .
14.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.
15.如图所示,有一块三角形的镜子,小明不小心弄破裂成1、2两块,现需配成同样大小的一块.为了方便起见,需带上 块,其理由是 .
16.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是 .
三、解答题
17.如图,A、B两个建筑分别位于河的两岸,要测得它们之间距离,可以从B出发沿河岸画一条射线BF,在BF上截取BC=CD,过D作DE∥AB,使E、A、C在同一条直线上,则DE长就是A、B之间的距离,请你说明道理.
18.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD,求证:AE=FB.
( http: / / www." \o "中国教育出版网 )
19.课间,小明拿着老师的等腰直角三角尺玩,不小心掉到两堆砖块之间,如图所示.
(1)求证:△ADC≌△CEB;
(2)已知DE=35cm,请你帮小明求出砖块的厚度a的大小(每块砖的厚度相同).
20.如图,已知△ABC中,∠1=∠2,AE=AD,求证:DF=EF.
参考答案
1.C
2.C
3.B
4.C
5.A
6.D.
7.C.
8.C.
9.D;
10.D;
11.答案为:AB=CD(答案不唯一).
12.答案为:AB=DE.
13.答案为:AAS.
14.答案为:4
15.答案为:第1,利用SAS得出全等三角形,即可配成与原来同样大小的一块.
16.答案为:(4,﹣1)或(﹣1,3)或(﹣1,﹣1)
17.解:∵DE∥AB
∴∠A=∠E
在ABC和EDC中
∴△ABC≌△EDC (AAS)
∴AB=DE
即DE长就是A、B之间距离
18.证明:∵CE∥DF
∴∠ECA=∠FDB,
在△ECA和△FDB中
( http: / / www." \o "中国教育出版网 ),
∴△ECA≌△FDB,
∴AE=FB.
19.(1)证明:由题意得:
AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
∠ADC=∠CEB,∠DAC=∠BCE,AC=BC
∴△ADC≌△CEB(AAS);
(2)解:由题意得:∵一块墙砖的厚度为a,
∴AD=4a,BE=3a,
由(1)得:△ADC≌△CEB,
∴DC=BE=3a,AD=CE=4a,
∴DC+CE=BE+AD=7a=42,
∴a=6,
答:砌墙砖块的厚度a为6cm.
20.证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC,
∵AE=AD,
∴AB﹣AD=AC﹣AE,即BD=CE,
在△BDF和△CEF中,
,
∴△BDF≌△CEF(AAS),
∴DF=EF.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
