2021-2022学年鲁教版(五四制)九年级数学下册5.3垂径定理 辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.3垂径定理 辅导训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 317.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 09:31:29 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学下册《5.3垂径定理》优生辅导训练(附答案)
1.下列语句中不正确的有( )
①长度相等的弧是等弧;
②垂直于弦的直径平分弦;
③圆是轴对称图形,任何一条直径都是它的对称轴;
④平分弦的直径也必平分弦所对的两条弧;
⑤弦所对的两条弧的中点连线垂直平分弦且过圆心.
A.1个 B.2个 C.3个 D.4个
2.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的半径为( )
A.8 B.10 C.16 D.20
3.如图,AB为⊙O的弦,点C为AB的中点,AB=8,OC=3,则⊙O的半径长为( )
A.4 B.5 C.6 D.7
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=1cm,CD=6cm,则AE为( )cm.
A.4 B.9 C.5 D.8
5.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
6.如图,⊙O的直径AB=20,CD是⊙O的弦,CD⊥AB,垂足为E,且BE:AE=1:4,则CD的长为( )
A.10 B.12 C.16 D.18
7.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于( )
A.5 B. C.2 D.
8.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为( )
A.2 B.2 C. D.
9.如图,将⊙O沿弦AB折叠,圆弧AB恰好经过圆心O,P是上一点,则∠APB的度数为( )
A.30° B.45° C.60° D.75°
10.⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
A.1cm B.7cm C.3cm或4cm D.1cm或7cm
11.如图,已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
12.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求线段AE的长.
13.已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D
(1)求证:AC=BD;
(2)若大圆的半径r=8,小圆的半径r=6,且圆心O到直线AB的距离为4,求AC的长.
14.如图,⊙O中的弦AB=6,CD过圆心O,且CD⊥AB于点D,CD=9,求圆的半径.
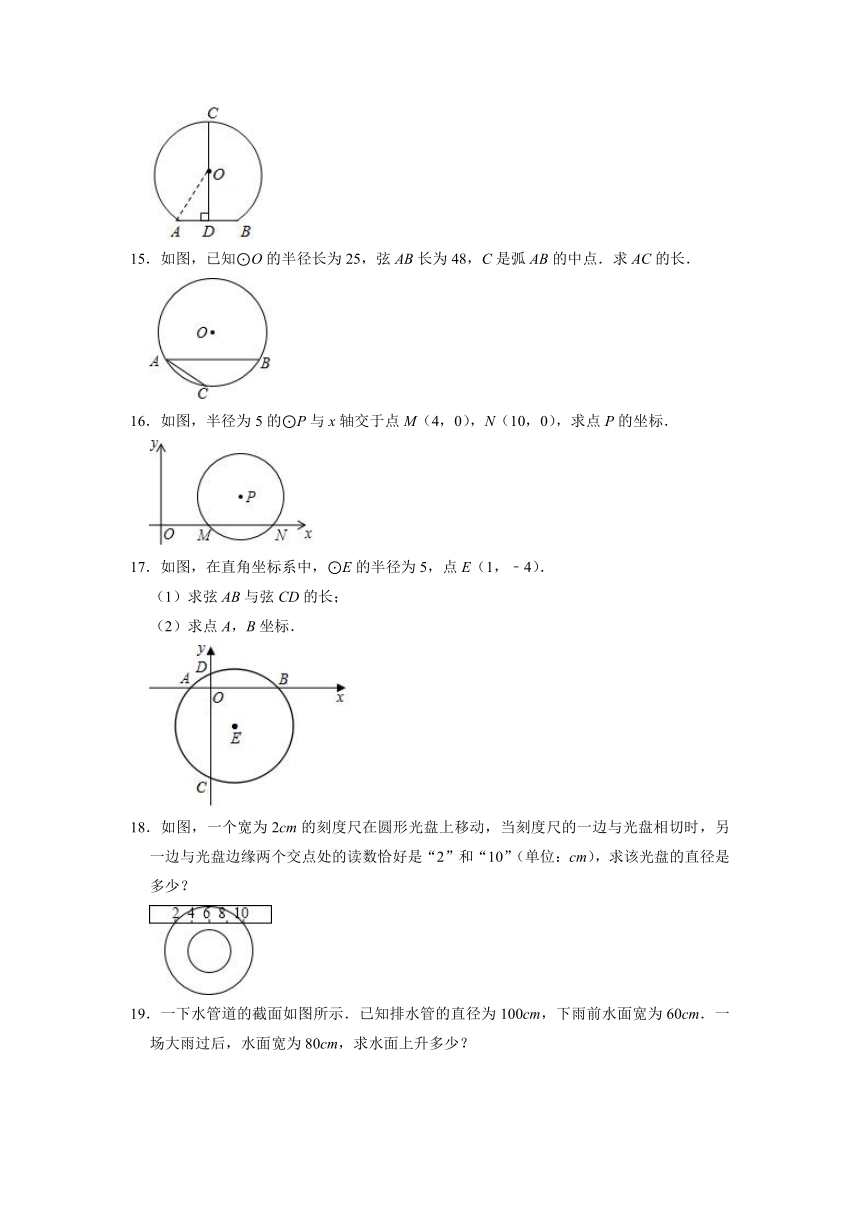
15.如图,已知⊙O的半径长为25,弦AB长为48,C是弧AB的中点.求AC的长.
16.如图,半径为5的⊙P与x轴交于点M(4,0),N(10,0),求点P的坐标.
17.如图,在直角坐标系中,⊙E的半径为5,点E(1,﹣4).
(1)求弦AB与弦CD的长;
(2)求点A,B坐标.
18.如图,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),求该光盘的直径是多少?
19.一下水管道的截面如图所示.已知排水管的直径为100cm,下雨前水面宽为60cm.一场大雨过后,水面宽为80cm,求水面上升多少?
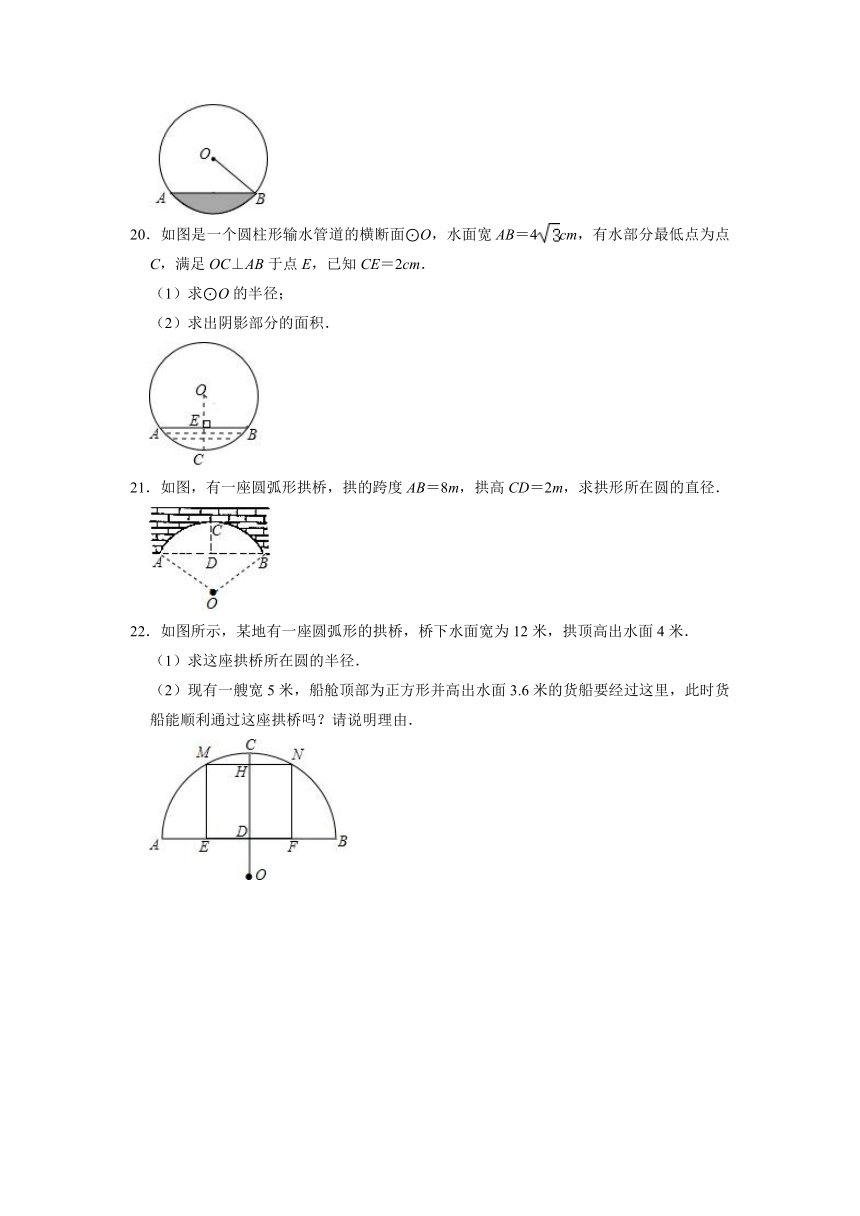
20.如图是一个圆柱形输水管道的横断面⊙O,水面宽AB=4cm,有水部分最低点为点C,满足OC⊥AB于点E,已知CE=2cm.
(1)求⊙O的半径;
(2)求出阴影部分的面积.
21.如图,有一座圆弧形拱桥,拱的跨度AB=8m,拱高CD=2m,求拱形所在圆的直径.
22.如图所示,某地有一座圆弧形的拱桥,桥下水面宽为12米,拱顶高出水面4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
参考答案
1.解:①∵能够完全重合的弧是等弧,
∴①不正确;
②∵垂直于弦的直径平分弦,
∴②正确;
③∵圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,
∴③不正确;
④∵平分弦(不是直径)的直径也必平分弦所对的两条弧,
∴④不正确
⑤∵弦所对的两条弧的中点连线垂直平分弦且过圆心,
∴⑤正确;
不正确的个数有3个,
故选:C.
2.解:连接OC,如图所示:
∵CD⊥AB,
∴CE=CD=6,
设⊙O的半径为x,则OE=x﹣2,
在Rt△OEC中,由勾股定理得:(x﹣2)2+62=x2
解得:x=10,
即⊙O的半径为10,
故选:B.
3.解:∵OC⊥AB于C,
∴AC=CB,
∵AB=8,
∴AC=CB=4,
在Rt△AOC中,OC=3,
根据勾股定理,
OA==5.
故选:B.
4.解:设OC=OB=xcm,
∵AB⊥CD,AB是直径,
∴EC=DE=3cm,
在Rt△OEC中,∵OC2=CE2+OE2,
∴x2=32+(x﹣1)2,
∴x=5,
∴OE=4cm,
∴AE=OA+OE=5+4=9cm,
故选:B.
5.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
6.解:连接OC,
∵直径AB=20,BE:AE=1:4,
∴OC=10,BE=4,
则OE=OB﹣BE=6,
∵CD⊥AB,
∴CD=2CE,∠OEC=90°,
∴CE===8,
∴CD=16,
故选:C.
7.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=2,
故选:C.
8.解:如图,连接OD,
∵CD⊥OC,
∴∠DCO=90°,
∴CD==,
当OC的值最小时,CD的值最大,
OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=2,
即CD的最大值为2,
故选:B.
9.解:作半径OC⊥AB于D,连接OA、OB,如图,
∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,
∴OD=CD,
∴OD=OC=OA,
∴∠OAD=30°,
又OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB=∠AOB=60°.
故选:C.
10.解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图1所示:
∵半径r=5cm,弦AB∥CD,且AB=8cm,CD=6cm,
∴OA=OC=5,CE=DE=3cm,AF=FB=4cm,E、F、O在一条直线上,
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE==4(cm),
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2,
∴OF==3(cm),
∴EF=OE+OF=4+3=7(cm),
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图2所示:
同①可得:OE=4cm,OF=3cm;
则AB与CD的距离为:OE﹣OF=1(cm).
故选:D.
11.解:如图所示:线段AB即为所求;
12.解:连接OC,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OA=5,
∵CD⊥AB,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
∴AE=OA﹣OE=5﹣3=2.
13.(1)证明:作OE⊥AB,则AE=BE,CE=DE,
故BE﹣DE=AE﹣CE;
即AC=BD;
(2)解:连接OC,OA,
∵OE⊥AB且OE⊥CD,
∴OE=4,CE=DE,
∴DE=CE===2,
AE===4,
∴AC=AE﹣CE=4﹣2.
14.解:设OA=OC=x,
∵OD⊥AB,
∴AD=DB=3,
在Rt△OAD中,∵OA2=OD2+AD2,
∴x2=((9﹣x)2+32,
∴x=5,
∴⊙O的半径为5.
15.解:如图,连接OA,OA交AB于H
∵C是弧AB的中点,
∴OH⊥AB,
在Rt△OAH中,OA=25,AH=24,
根据勾股定理得:OH==7,
∴HC=OC﹣OH=25﹣7=18,
在Rt△AHC中,根据勾股定理得:AC==30,
∴AC的长为30.
16.解:过点P作PA⊥MN,于点A,
∵M(4,0),N(10,0),
∴MN=6,
∵半径为5,PA⊥MN,
∴MA=3,则PA==4,AO=7,
∴P点坐标为:(7,4).
17.解:(1)如图所示,过E作EF⊥AB于F,作EG⊥CD于G,则BF=AB,CG=CD,
∵⊙E的半径为5,E(1,﹣4),
∴BE=5,EF=4,GE=1,
∴Rt△BEF中,BF==3,
Rt△CEG中,CG==2,
∴AB=2BF=6,CD=2CG=4;
(2)如图所示,∵E(1,﹣4),EF⊥AB,
∴F(1,0),
又∵AF=BF=3,
∴OB=1+3=4,AO=3﹣1=2,
∴A(﹣2,0),B(4,0).
18.解:过点O作OA垂直直尺与点A,连接OB,设OB=rcm,
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,
∴AB=4cm,
∵刻度尺宽2cm,
∴OA=(r﹣2)cm,
在Rt△OAB中,
OA2+AB2=OB2,即(r﹣2)2+42=r2,
解得r=5,
则该光盘的直径是10cm.
19.解:作半径OD⊥AB交AB于C,连接OB,如图所示,
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下,水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
20.解:(1)连接OA
设半径为r,则OE=r﹣2,
∵OE⊥AB,
∴AE=AB=2,
在Rt△OAE中,,
解得:r=4;
(2)在Rt△OAE中,OE=2,OA=4,
∴∠EOA=60°,
∵OE⊥AB,
∴,
∴∠AOB=120°,
∴阴影部分的面积=.
21.解:如图所示,连接OD,由题意O、D、C共线.
∵AB⊥CO,
∴AB=2AD,
∵AB=8m,CD=2m,
∴AD=4m,
设OA=r,则OD=r﹣2,
在Rt△AOD中,
∵OA2=AD2+OD2,即r2=42+(r﹣2)2,解得r=5m.
∴拱形所在圆的直径为10cm.
22.解:(1)连接OA,
根据题意得:CD=4米,AB=12米,
则AD=AB=6(米),
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC﹣CD=(x﹣4)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x﹣4)2+62,
解得:x=6.5,
故这座拱桥所在圆的半径为6.5米.
(2)货船不能顺利通过这座拱桥.理由:
连接OM,
设MN=5米,
∵OC⊥MN,
∴MH=MN=2.5(米),
在Rt△OMH中,OH==6(米),
∵OD=OC﹣CD=6.5﹣4=2.5(米)
∵OH﹣OD=6﹣2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.
1.下列语句中不正确的有( )
①长度相等的弧是等弧;
②垂直于弦的直径平分弦;
③圆是轴对称图形,任何一条直径都是它的对称轴;
④平分弦的直径也必平分弦所对的两条弧;
⑤弦所对的两条弧的中点连线垂直平分弦且过圆心.
A.1个 B.2个 C.3个 D.4个
2.如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的半径为( )
A.8 B.10 C.16 D.20
3.如图,AB为⊙O的弦,点C为AB的中点,AB=8,OC=3,则⊙O的半径长为( )
A.4 B.5 C.6 D.7
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,BE=1cm,CD=6cm,则AE为( )cm.
A.4 B.9 C.5 D.8
5.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
6.如图,⊙O的直径AB=20,CD是⊙O的弦,CD⊥AB,垂足为E,且BE:AE=1:4,则CD的长为( )
A.10 B.12 C.16 D.18
7.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于( )
A.5 B. C.2 D.
8.如图,在圆O中,弦AB=4,点C在AB上移动,连接OC,过点C做CD⊥OC交圆O于点D,则CD的最大值为( )
A.2 B.2 C. D.
9.如图,将⊙O沿弦AB折叠,圆弧AB恰好经过圆心O,P是上一点,则∠APB的度数为( )
A.30° B.45° C.60° D.75°
10.⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
A.1cm B.7cm C.3cm或4cm D.1cm或7cm
11.如图,已知⊙O与⊙O内一定点P,请用尺规作图法求作经过点P的最短弦AB.(保留作图痕迹,不写作法)
12.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,求线段AE的长.
13.已知在以点O为圆心的两个同心圆中,大圆的弦交小圆于点C、D
(1)求证:AC=BD;
(2)若大圆的半径r=8,小圆的半径r=6,且圆心O到直线AB的距离为4,求AC的长.
14.如图,⊙O中的弦AB=6,CD过圆心O,且CD⊥AB于点D,CD=9,求圆的半径.
15.如图,已知⊙O的半径长为25,弦AB长为48,C是弧AB的中点.求AC的长.
16.如图,半径为5的⊙P与x轴交于点M(4,0),N(10,0),求点P的坐标.
17.如图,在直角坐标系中,⊙E的半径为5,点E(1,﹣4).
(1)求弦AB与弦CD的长;
(2)求点A,B坐标.
18.如图,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),求该光盘的直径是多少?
19.一下水管道的截面如图所示.已知排水管的直径为100cm,下雨前水面宽为60cm.一场大雨过后,水面宽为80cm,求水面上升多少?
20.如图是一个圆柱形输水管道的横断面⊙O,水面宽AB=4cm,有水部分最低点为点C,满足OC⊥AB于点E,已知CE=2cm.
(1)求⊙O的半径;
(2)求出阴影部分的面积.
21.如图,有一座圆弧形拱桥,拱的跨度AB=8m,拱高CD=2m,求拱形所在圆的直径.
22.如图所示,某地有一座圆弧形的拱桥,桥下水面宽为12米,拱顶高出水面4米.
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽5米,船舱顶部为正方形并高出水面3.6米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
参考答案
1.解:①∵能够完全重合的弧是等弧,
∴①不正确;
②∵垂直于弦的直径平分弦,
∴②正确;
③∵圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,
∴③不正确;
④∵平分弦(不是直径)的直径也必平分弦所对的两条弧,
∴④不正确
⑤∵弦所对的两条弧的中点连线垂直平分弦且过圆心,
∴⑤正确;
不正确的个数有3个,
故选:C.
2.解:连接OC,如图所示:
∵CD⊥AB,
∴CE=CD=6,
设⊙O的半径为x,则OE=x﹣2,
在Rt△OEC中,由勾股定理得:(x﹣2)2+62=x2
解得:x=10,
即⊙O的半径为10,
故选:B.
3.解:∵OC⊥AB于C,
∴AC=CB,
∵AB=8,
∴AC=CB=4,
在Rt△AOC中,OC=3,
根据勾股定理,
OA==5.
故选:B.
4.解:设OC=OB=xcm,
∵AB⊥CD,AB是直径,
∴EC=DE=3cm,
在Rt△OEC中,∵OC2=CE2+OE2,
∴x2=32+(x﹣1)2,
∴x=5,
∴OE=4cm,
∴AE=OA+OE=5+4=9cm,
故选:B.
5.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
6.解:连接OC,
∵直径AB=20,BE:AE=1:4,
∴OC=10,BE=4,
则OE=OB﹣BE=6,
∵CD⊥AB,
∴CD=2CE,∠OEC=90°,
∴CE===8,
∴CD=16,
故选:C.
7.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=2,
故选:C.
8.解:如图,连接OD,
∵CD⊥OC,
∴∠DCO=90°,
∴CD==,
当OC的值最小时,CD的值最大,
OC⊥AB时,OC最小,此时D、B两点重合,
∴CD=CB=AB=2,
即CD的最大值为2,
故选:B.
9.解:作半径OC⊥AB于D,连接OA、OB,如图,
∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,
∴OD=CD,
∴OD=OC=OA,
∴∠OAD=30°,
又OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB=∠AOB=60°.
故选:C.
10.解:①当AB、CD在圆心两侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图1所示:
∵半径r=5cm,弦AB∥CD,且AB=8cm,CD=6cm,
∴OA=OC=5,CE=DE=3cm,AF=FB=4cm,E、F、O在一条直线上,
在Rt△OEC中,由勾股定理可得:
OE2=OC2﹣CE2
∴OE==4(cm),
在Rt△OFA中,由勾股定理可得:
OF2=OA2﹣AF2,
∴OF==3(cm),
∴EF=OE+OF=4+3=7(cm),
AB与CD的距离为7;
②当AB、CD在圆心同侧时;
过O作OE⊥CD交CD于E点,过O作OF⊥AB交AB于F点,连接OA、OC,如图2所示:
同①可得:OE=4cm,OF=3cm;
则AB与CD的距离为:OE﹣OF=1(cm).
故选:D.
11.解:如图所示:线段AB即为所求;
12.解:连接OC,如图,
∵AB是⊙O的直径,AB=10,
∴OC=OA=5,
∵CD⊥AB,
∴CE=DE=CD=×8=4,
在Rt△OCE中,OC=5,CE=4,
∴OE==3,
∴AE=OA﹣OE=5﹣3=2.
13.(1)证明:作OE⊥AB,则AE=BE,CE=DE,
故BE﹣DE=AE﹣CE;
即AC=BD;
(2)解:连接OC,OA,
∵OE⊥AB且OE⊥CD,
∴OE=4,CE=DE,
∴DE=CE===2,
AE===4,
∴AC=AE﹣CE=4﹣2.
14.解:设OA=OC=x,
∵OD⊥AB,
∴AD=DB=3,
在Rt△OAD中,∵OA2=OD2+AD2,
∴x2=((9﹣x)2+32,
∴x=5,
∴⊙O的半径为5.
15.解:如图,连接OA,OA交AB于H
∵C是弧AB的中点,
∴OH⊥AB,
在Rt△OAH中,OA=25,AH=24,
根据勾股定理得:OH==7,
∴HC=OC﹣OH=25﹣7=18,
在Rt△AHC中,根据勾股定理得:AC==30,
∴AC的长为30.
16.解:过点P作PA⊥MN,于点A,
∵M(4,0),N(10,0),
∴MN=6,
∵半径为5,PA⊥MN,
∴MA=3,则PA==4,AO=7,
∴P点坐标为:(7,4).
17.解:(1)如图所示,过E作EF⊥AB于F,作EG⊥CD于G,则BF=AB,CG=CD,
∵⊙E的半径为5,E(1,﹣4),
∴BE=5,EF=4,GE=1,
∴Rt△BEF中,BF==3,
Rt△CEG中,CG==2,
∴AB=2BF=6,CD=2CG=4;
(2)如图所示,∵E(1,﹣4),EF⊥AB,
∴F(1,0),
又∵AF=BF=3,
∴OB=1+3=4,AO=3﹣1=2,
∴A(﹣2,0),B(4,0).
18.解:过点O作OA垂直直尺与点A,连接OB,设OB=rcm,
∵一边与光盘边缘两个交点处的读数恰好是“2”和“10”,
∴AB=4cm,
∵刻度尺宽2cm,
∴OA=(r﹣2)cm,
在Rt△OAB中,
OA2+AB2=OB2,即(r﹣2)2+42=r2,
解得r=5,
则该光盘的直径是10cm.
19.解:作半径OD⊥AB交AB于C,连接OB,如图所示,
由垂径定理得:BC=AB=30cm,
在Rt△OBC中,OC==40cm,
当水位上升到圆心以下,水面宽80cm时,
则OC′==30cm,
水面上升的高度为:40﹣30=10cm;
当水位上升到圆心以上时,水面上升的高度为:40+30=70cm,
综上可得,水面上升的高度为10cm或70cm.
20.解:(1)连接OA
设半径为r,则OE=r﹣2,
∵OE⊥AB,
∴AE=AB=2,
在Rt△OAE中,,
解得:r=4;
(2)在Rt△OAE中,OE=2,OA=4,
∴∠EOA=60°,
∵OE⊥AB,
∴,
∴∠AOB=120°,
∴阴影部分的面积=.
21.解:如图所示,连接OD,由题意O、D、C共线.
∵AB⊥CO,
∴AB=2AD,
∵AB=8m,CD=2m,
∴AD=4m,
设OA=r,则OD=r﹣2,
在Rt△AOD中,
∵OA2=AD2+OD2,即r2=42+(r﹣2)2,解得r=5m.
∴拱形所在圆的直径为10cm.
22.解:(1)连接OA,
根据题意得:CD=4米,AB=12米,
则AD=AB=6(米),
设这座拱桥所在圆的半径为x米,
则OA=OC=x米,OD=OC﹣CD=(x﹣4)米,
在Rt△AOD中,OA2=OD2+AD2,
则x2=(x﹣4)2+62,
解得:x=6.5,
故这座拱桥所在圆的半径为6.5米.
(2)货船不能顺利通过这座拱桥.理由:
连接OM,
设MN=5米,
∵OC⊥MN,
∴MH=MN=2.5(米),
在Rt△OMH中,OH==6(米),
∵OD=OC﹣CD=6.5﹣4=2.5(米)
∵OH﹣OD=6﹣2.5=3.5(米)<3.6米,
∴货船不能顺利通过这座拱桥.
