2021——2022学年人教版九年级数学下册28.1 锐角三角函数-正弦 同步练习(word版含答案)
文档属性
| 名称 | 2021——2022学年人教版九年级数学下册28.1 锐角三角函数-正弦 同步练习(word版含答案) | 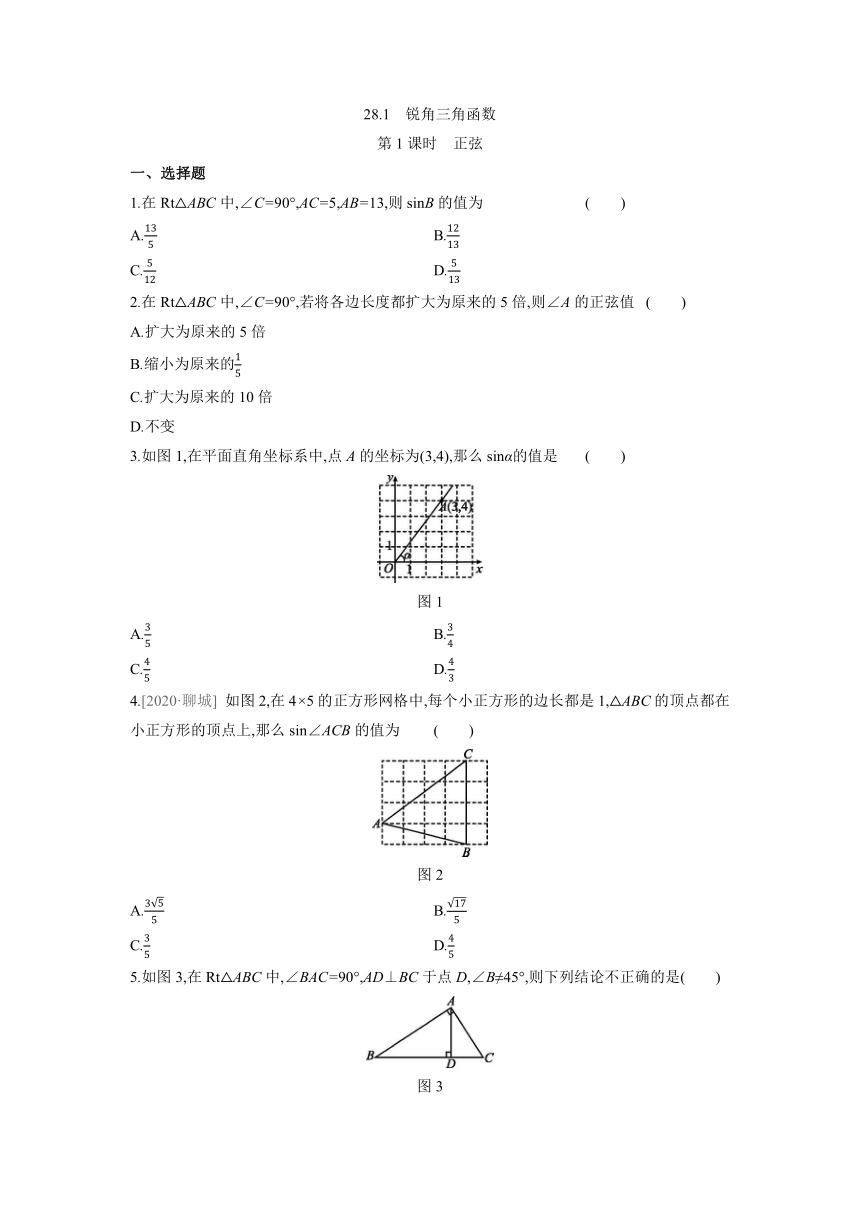 | |
| 格式 | docx | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 13:00:30 | ||
图片预览



文档简介
28.1 锐角三角函数
第1课时 正弦
一、选择题
1.在Rt△ABC中,∠C=90°,AC=5,AB=13,则sinB的值为 ( )
A. B.
C. D.
2.在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的5倍,则∠A的正弦值 ( )
A.扩大为原来的5倍
B.缩小为原来的
C.扩大为原来的10倍
D.不变
3.如图1,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是 ( )
图1
A. B.
C. D.
4.[2020·聊城] 如图2,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在小正方形的顶点上,那么sin∠ACB的值为 ( )
图2
A. B.
C. D.
5.如图3,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠B≠45°,则下列结论不正确的是( )
图3
A.sinB= B.sinB= C.sinB= D.sinB=
6.[2020·南充] 如图4所示,点A,B,C均在正方形网格的格点上,则sin∠BAC的值为 ( )
图4
A. B. C. D.
7.如图5,四边形ABCD内接于☉O,AB为直径,AD=CD.过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB=,DF=5,则BC的长为( )
图5
A.8 B.10 C.12 D.16
二、填空题
8.在Rt△ABC中,∠C=90°,AC∶BC=1∶2,则sinB= .
9.如图6,在△ABC中,∠C=90°,sinA=,则sinB= .
图6
10.在Rt△ABC中,∠ACB=90°,CD是斜边AB的中线,CD=4,AC=6,则sinB的值是 .
11.如图7,在☉O中,过直径AB延长线上的点C作☉O的一条切线,切点为D,连接OD.若AC=7,AB=4,则sinC的值为 .
图7
12.如图8,☉O是△ABC的外接圆,AD是☉O的直径.若☉O的半径为,AC=2,则sinB的值是 .
图8
13.如图9,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为 .
图9
三、解答题
14.在Rt△ABC中,∠C=90°,AC=1 cm,BC=2 cm,求sinA和sinB的值.
15.在Rt△ABC中,∠C=90°.
(1)若sinA=,BC=9,求AB的长;
(2)若sinB=,AB=10,求BC的长.
16.如图10,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,求sin∠BCD的值.
图10
17.已知:如图11,在△ABC中,AB=AC=13,BC=10.求∠BAC,∠ABC的正弦值.
图11
答案
1.D 2.D 3.C
4.D [解析]利用网格特征把∠ACB放置于直角三角形中再求正弦值.如图,在Rt△ACD中,由勾股定理,得AC===5,于是sin∠ACB==.
5.C
6.B [解析]如图,过点B作BD⊥AC于点D,则∠ADB=90°.设小正方形网格的边长均为1,根据勾股定理,得AB==,AC==3.
∵S△ABC=BC·3=AC·BD,
∴BD==,
∴在Rt△ABD中,sin∠BAC===.故选B.
7.C [解析]如图,连接BD.
∵AD=CD,
∴∠DAC=∠ACD.
∵AB为☉O的直径,
∴∠ADB=∠ACB=90°,
∴∠DAB+∠ABD=90°.
∵DE⊥AB,∴∠DAB+∠ADE=90°,
∴∠ADE=∠ABD.
∵∠ABD=∠ACD,
∴∠DAC=∠ADE,
∴AF=DF=5.
在Rt△AEF中,sin∠EAF==,
∴EF=3.由勾股定理可得AE=4,
∴DE=3+5=8.
易证△ADE∽△DBE,则=,
∴BE===16,
∴AB=16+4=20.
∵在Rt△ABC中,sin∠CAB==,
∴BC=12.
8. [解析]设AC=k,则BC=2k,由勾股定理,得AB==k,再由正弦的定义,得sinB=.
9.
10. [解析]∵在Rt△ABC中,CD是斜边AB的中线,CD=4,
∴AB=2CD=8,则sinB===.
11.
12. [解析]如图,连接CD.
∵AD是☉O的直径,
∴∠ACD=90°.
∵☉O的半径为,
∴AD=3,
∴在Rt△ACD中,sinD==.
又∵∠B=∠D,
∴sinB=sinD=.
13. [解析]由折叠的性质可知∠AFE=∠D=90°,AF=AD=5,
∴∠AFB+∠EFC=90°,BF==4.
∵∠AFB+∠BAF=90°,
∴∠EFC=∠BAF,
∴sin∠EFC=sin∠BAF==.
14.解:在Rt△ABC中,由勾股定理,得
AB===(cm),
∴sinA===,
sinB===.
故sinA=,sinB=.
15.解:(1)∵sinA=,∴=,
即=,∴AB=15.
(2)∵sinB=,∴=,
即=,∴AC=8,
∴BC===6.
16.解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠B=90°,∠BCD+∠B=90°,
∴∠A=∠BCD,
∴sin∠BCD=sinA==.
17.解:如图,过点A作AD⊥BC于点D,过点B作BE⊥AC于点E.
∵AB=AC,BC=10,
∴BD=BC=5.
∵AB=13,
∴AD===12,
∴sin∠ABC==.
∵S△ABC=BC·AD=AC·BE,
∴BE=,
∴sin∠BAC===.
故sin∠BAC=,sin∠ABC=.
第1课时 正弦
一、选择题
1.在Rt△ABC中,∠C=90°,AC=5,AB=13,则sinB的值为 ( )
A. B.
C. D.
2.在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的5倍,则∠A的正弦值 ( )
A.扩大为原来的5倍
B.缩小为原来的
C.扩大为原来的10倍
D.不变
3.如图1,在平面直角坐标系中,点A的坐标为(3,4),那么sinα的值是 ( )
图1
A. B.
C. D.
4.[2020·聊城] 如图2,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在小正方形的顶点上,那么sin∠ACB的值为 ( )
图2
A. B.
C. D.
5.如图3,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠B≠45°,则下列结论不正确的是( )
图3
A.sinB= B.sinB= C.sinB= D.sinB=
6.[2020·南充] 如图4所示,点A,B,C均在正方形网格的格点上,则sin∠BAC的值为 ( )
图4
A. B. C. D.
7.如图5,四边形ABCD内接于☉O,AB为直径,AD=CD.过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB=,DF=5,则BC的长为( )
图5
A.8 B.10 C.12 D.16
二、填空题
8.在Rt△ABC中,∠C=90°,AC∶BC=1∶2,则sinB= .
9.如图6,在△ABC中,∠C=90°,sinA=,则sinB= .
图6
10.在Rt△ABC中,∠ACB=90°,CD是斜边AB的中线,CD=4,AC=6,则sinB的值是 .
11.如图7,在☉O中,过直径AB延长线上的点C作☉O的一条切线,切点为D,连接OD.若AC=7,AB=4,则sinC的值为 .
图7
12.如图8,☉O是△ABC的外接圆,AD是☉O的直径.若☉O的半径为,AC=2,则sinB的值是 .
图8
13.如图9,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么sin∠EFC的值为 .
图9
三、解答题
14.在Rt△ABC中,∠C=90°,AC=1 cm,BC=2 cm,求sinA和sinB的值.
15.在Rt△ABC中,∠C=90°.
(1)若sinA=,BC=9,求AB的长;
(2)若sinB=,AB=10,求BC的长.
16.如图10,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,CD⊥AB于点D,求sin∠BCD的值.
图10
17.已知:如图11,在△ABC中,AB=AC=13,BC=10.求∠BAC,∠ABC的正弦值.
图11
答案
1.D 2.D 3.C
4.D [解析]利用网格特征把∠ACB放置于直角三角形中再求正弦值.如图,在Rt△ACD中,由勾股定理,得AC===5,于是sin∠ACB==.
5.C
6.B [解析]如图,过点B作BD⊥AC于点D,则∠ADB=90°.设小正方形网格的边长均为1,根据勾股定理,得AB==,AC==3.
∵S△ABC=BC·3=AC·BD,
∴BD==,
∴在Rt△ABD中,sin∠BAC===.故选B.
7.C [解析]如图,连接BD.
∵AD=CD,
∴∠DAC=∠ACD.
∵AB为☉O的直径,
∴∠ADB=∠ACB=90°,
∴∠DAB+∠ABD=90°.
∵DE⊥AB,∴∠DAB+∠ADE=90°,
∴∠ADE=∠ABD.
∵∠ABD=∠ACD,
∴∠DAC=∠ADE,
∴AF=DF=5.
在Rt△AEF中,sin∠EAF==,
∴EF=3.由勾股定理可得AE=4,
∴DE=3+5=8.
易证△ADE∽△DBE,则=,
∴BE===16,
∴AB=16+4=20.
∵在Rt△ABC中,sin∠CAB==,
∴BC=12.
8. [解析]设AC=k,则BC=2k,由勾股定理,得AB==k,再由正弦的定义,得sinB=.
9.
10. [解析]∵在Rt△ABC中,CD是斜边AB的中线,CD=4,
∴AB=2CD=8,则sinB===.
11.
12. [解析]如图,连接CD.
∵AD是☉O的直径,
∴∠ACD=90°.
∵☉O的半径为,
∴AD=3,
∴在Rt△ACD中,sinD==.
又∵∠B=∠D,
∴sinB=sinD=.
13. [解析]由折叠的性质可知∠AFE=∠D=90°,AF=AD=5,
∴∠AFB+∠EFC=90°,BF==4.
∵∠AFB+∠BAF=90°,
∴∠EFC=∠BAF,
∴sin∠EFC=sin∠BAF==.
14.解:在Rt△ABC中,由勾股定理,得
AB===(cm),
∴sinA===,
sinB===.
故sinA=,sinB=.
15.解:(1)∵sinA=,∴=,
即=,∴AB=15.
(2)∵sinB=,∴=,
即=,∴AC=8,
∴BC===6.
16.解:∵∠ACB=90°,CD⊥AB,
∴∠A+∠B=90°,∠BCD+∠B=90°,
∴∠A=∠BCD,
∴sin∠BCD=sinA==.
17.解:如图,过点A作AD⊥BC于点D,过点B作BE⊥AC于点E.
∵AB=AC,BC=10,
∴BD=BC=5.
∵AB=13,
∴AD===12,
∴sin∠ABC==.
∵S△ABC=BC·AD=AC·BE,
∴BE=,
∴sin∠BAC===.
故sin∠BAC=,sin∠ABC=.
