2021--2022学年湘教版九年级数学上册第2章 一元二次方程 检测试卷(word版含答案)
文档属性
| 名称 | 2021--2022学年湘教版九年级数学上册第2章 一元二次方程 检测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 191.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 13:03:33 | ||
图片预览


文档简介
湘教版数学九上 第2章 一元二次方程 检测试卷A卷(有答案)
一、选择题(每小题3分,共24分)
1. 某校羽毛球队有若干名队员,任意两名队员之间进行一场友谊赛,共进行了36场比赛.如果全队有名队员,根据题意下列方程正确的是( )
A. B.
C. D.
2. 已知一元二次方程,则该方程根的情况是
A.有两个不相等的实数根 B.有两个相等的实数根
C.两个根都是自然数 D.无实数根
3.一元二次方程x +4x-3=0的两根为x1,x2,则x1·x2+x1+x2的值时( )
A.1 B.7
C.-4 D.-7
4.若一元二次方程x2+2x+a=0有实数解,则a的取值范围是
A.a<1 B. a≤4
C.a≤1 D.a≥1
5.关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是( )
A.m≤3 B.m<3
C.m<3且m≠2 D.m≤3且m≠2
6.用配方法解方程x2-6x-8=0时,配方结果正确的是( )
A. B.
C. D.
7.若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m-1的图像不经过第( )象限。
A. 四 B. 三
C. 二 D.一
8.已知三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形的周长是( )
A.14 B.12
C.12或14 D.以上都不对
二.填空题(每小题3分,共30分)
9.若关于x的一元二次方程4x2-4x+c=0有两个相等的实数根,则c的值是
10.将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3,则原铁皮的边长为
11.如果x2-x-1=(x+1)0,那么x的值为( )
12.学校标准化建设,2019年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2021年投资7.2亿元人民币,那么每年投资的增长率为
13. 设、是一元二次方程的两实数根,则的值为 .
14.一元二次方程的解是 。
15.某商品每件元,经过两次降价后,售价为元,若每次降价的百分比相同,则第一次降价后的售价为每件__________元.
16.若x2-3x+1=0,则的值为________.
17.如果关于x的一元二次方程没有实数根,那么m的取值范围是________.
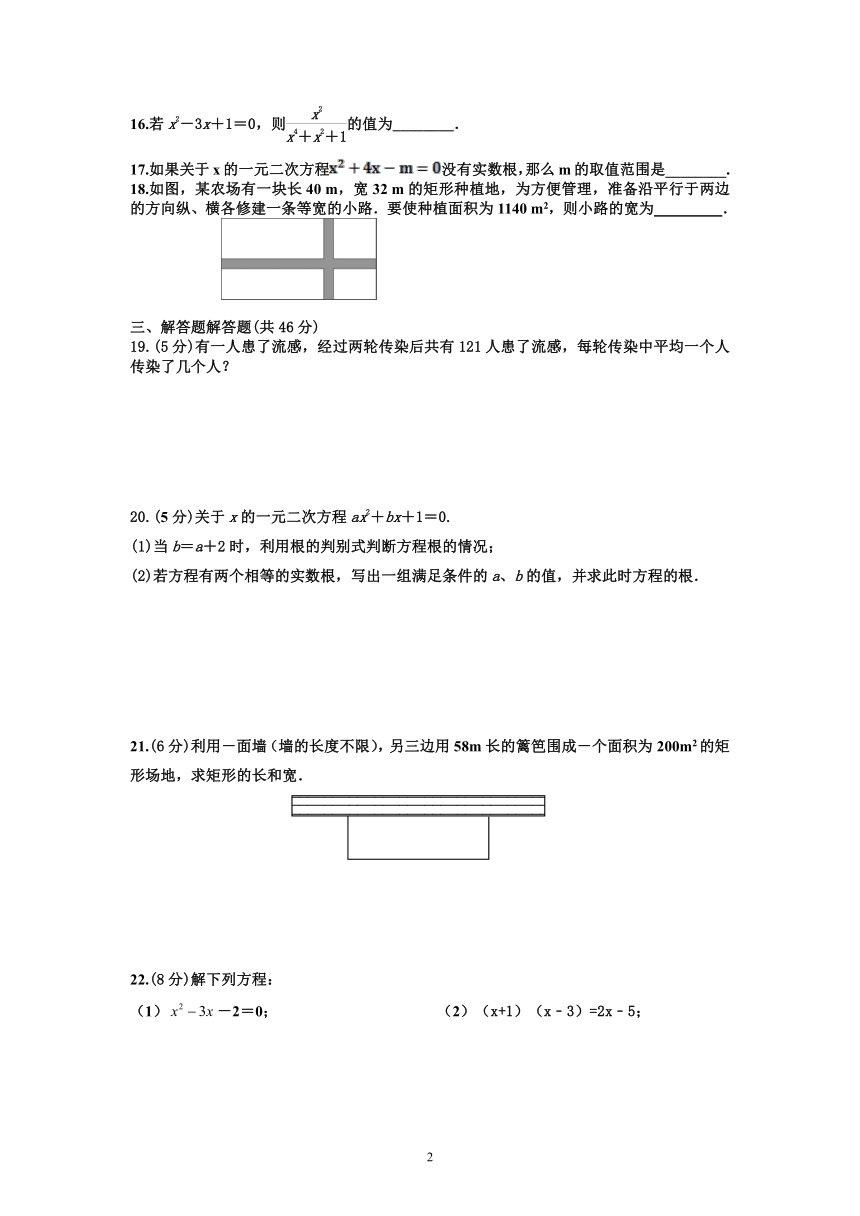
18.如图,某农场有一块长40 m,宽32 m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路.要使种植面积为1140 m2,则小路的宽为 .
三、解答题解答题(共46分)
19.(5分)有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
20.(5分)关于x的一元二次方程ax2+bx+1=0.
(1)当b=a+2时,利用根的判别式判断方程根的情况;
(2)若方程有两个相等的实数根,写出一组满足条件的a、b的值,并求此时方程的根.
21.(6分)利用-面墙(墙的长度不限),另三边用58m长的篱笆围成-个面积为200m2的矩形场地,求矩形的长和宽.
22.(8分)解下列方程:
(1)-2=0; (2)(x+1)(x﹣3)=2x﹣5;
(3)3x2﹣5x﹣2=0 (4)2x2﹣4x﹣1998=0.
23.(6分)如图,在长为10 cm,宽为8 cm的长方形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原长方形面积的80%,求截去的小正方形的边长.
24.(8分)在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) … 34.8 32 29.6 28 …
售价x(元/千克) … 22.6 24 25.2 26 …
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
25.(8分)某公司投资新建了一个商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?
一、选择题
1 2 3 4 5 6 7 8
C A D C D A D B
二.填空题
9 10 11 12 13 14 15 16 17 18
1 10 2 20﹪ 27 0或2 270 2
三、解答题
19.解:设每轮传染中平均每个人传染了x人,
依题意得1+x+x(1+x)=121,
∴x=10或x=﹣12(不合题意,舍去).
∴每轮传染中平均一个人传染了10个人
有两个相等的实数根,
∴△,
∴,
∴或.
20.解:(1)由题意知a≠0,
b2-4a=(a+2)2-4a=a2+4a+4-4a=a2+4.
∵a2>0,∴a2+4>0.
∴方程有两个不相等的实数根.
(2)∵方程有两个相等的实数根,
∴b2-4a=0,
若b=2,a=1,则方程为x2+2x+1=0,解得x1=x2=-1.(答案不唯一)
21.解:设垂直于墙的-边为米,得:
=200.
解得:=25,=4.
∴另-边为8米或50米.
答:矩形长为25米宽为8米或矩形长为50米宽为4米.
(1)-2=0,
∵a=1,b=-3,c=-2
∴△==17,
∴,
(2)整理得:x2﹣2x﹣3=2x﹣5,
则x2﹣4x+2=0,
(x﹣2)2=2,
解得:x1=2+,x2=2﹣,
(3)3x2﹣5x﹣2=0,
x2﹣x=,
x2﹣x+=+,
(x﹣)2=,
x﹣=±,
解得x1=﹣,x2=2;
(4)2x2﹣4x﹣1998=0,
x2﹣2x=999,
x2﹣2x+1=1000,
(x﹣1)2=1000,
x﹣1=±10,
解得x1=1﹣10,x2=1+10.
23.解:设截去的小正方形的边长为x cm,由题意得10×8-4x2=80%×10×8,
解得x1=2,x2=-2(不合题意,舍去).
所以x=2.
答:截去的小正方形的边长为2 cm.
24.解 (1)设y与x之间的函数关系式为y=kx+b,
将(22.6,34.8)、(24,32)代入y=kx+b,
,解得:,
∴y与x之间的函数关系式为y=﹣2x+80.
当x=23.5时,y=﹣2x+80=33.
答:当天该水果的销售量为33千克.
(2)根据题意得:(x﹣20)(﹣2x+80)=150,
解得:x1=35,x2=25.
∵20≤x≤32,
∴x=25.
答:如果某天销售这种水果获利150元,那么该天水果的售价为25元.
25.解:(1)∵(130 000-100 000)÷5 000=6(间),30-6=24(间),∴能租出24间.
(2)设每间商铺的年租金增加x万元,则
整理,得2x2-11x+5=0,解得x1=5,
x2=0.5,5+10=15(万元),0.5+10=10.5(万元).
∴当每间商铺的年租金定为10.5万元或15万元时,该公司的年收益为275万元.
一、选择题(每小题3分,共24分)
1. 某校羽毛球队有若干名队员,任意两名队员之间进行一场友谊赛,共进行了36场比赛.如果全队有名队员,根据题意下列方程正确的是( )
A. B.
C. D.
2. 已知一元二次方程,则该方程根的情况是
A.有两个不相等的实数根 B.有两个相等的实数根
C.两个根都是自然数 D.无实数根
3.一元二次方程x +4x-3=0的两根为x1,x2,则x1·x2+x1+x2的值时( )
A.1 B.7
C.-4 D.-7
4.若一元二次方程x2+2x+a=0有实数解,则a的取值范围是
A.a<1 B. a≤4
C.a≤1 D.a≥1
5.关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是( )
A.m≤3 B.m<3
C.m<3且m≠2 D.m≤3且m≠2
6.用配方法解方程x2-6x-8=0时,配方结果正确的是( )
A. B.
C. D.
7.若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m-1的图像不经过第( )象限。
A. 四 B. 三
C. 二 D.一
8.已知三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形的周长是( )
A.14 B.12
C.12或14 D.以上都不对
二.填空题(每小题3分,共30分)
9.若关于x的一元二次方程4x2-4x+c=0有两个相等的实数根,则c的值是
10.将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3,则原铁皮的边长为
11.如果x2-x-1=(x+1)0,那么x的值为( )
12.学校标准化建设,2019年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2021年投资7.2亿元人民币,那么每年投资的增长率为
13. 设、是一元二次方程的两实数根,则的值为 .
14.一元二次方程的解是 。
15.某商品每件元,经过两次降价后,售价为元,若每次降价的百分比相同,则第一次降价后的售价为每件__________元.
16.若x2-3x+1=0,则的值为________.
17.如果关于x的一元二次方程没有实数根,那么m的取值范围是________.
18.如图,某农场有一块长40 m,宽32 m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路.要使种植面积为1140 m2,则小路的宽为 .
三、解答题解答题(共46分)
19.(5分)有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?
20.(5分)关于x的一元二次方程ax2+bx+1=0.
(1)当b=a+2时,利用根的判别式判断方程根的情况;
(2)若方程有两个相等的实数根,写出一组满足条件的a、b的值,并求此时方程的根.
21.(6分)利用-面墙(墙的长度不限),另三边用58m长的篱笆围成-个面积为200m2的矩形场地,求矩形的长和宽.
22.(8分)解下列方程:
(1)-2=0; (2)(x+1)(x﹣3)=2x﹣5;
(3)3x2﹣5x﹣2=0 (4)2x2﹣4x﹣1998=0.
23.(6分)如图,在长为10 cm,宽为8 cm的长方形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原长方形面积的80%,求截去的小正方形的边长.
24.(8分)在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) … 34.8 32 29.6 28 …
售价x(元/千克) … 22.6 24 25.2 26 …
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
25.(8分)某公司投资新建了一个商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?
一、选择题
1 2 3 4 5 6 7 8
C A D C D A D B
二.填空题
9 10 11 12 13 14 15 16 17 18
1 10 2 20﹪ 27 0或2 270 2
三、解答题
19.解:设每轮传染中平均每个人传染了x人,
依题意得1+x+x(1+x)=121,
∴x=10或x=﹣12(不合题意,舍去).
∴每轮传染中平均一个人传染了10个人
有两个相等的实数根,
∴△,
∴,
∴或.
20.解:(1)由题意知a≠0,
b2-4a=(a+2)2-4a=a2+4a+4-4a=a2+4.
∵a2>0,∴a2+4>0.
∴方程有两个不相等的实数根.
(2)∵方程有两个相等的实数根,
∴b2-4a=0,
若b=2,a=1,则方程为x2+2x+1=0,解得x1=x2=-1.(答案不唯一)
21.解:设垂直于墙的-边为米,得:
=200.
解得:=25,=4.
∴另-边为8米或50米.
答:矩形长为25米宽为8米或矩形长为50米宽为4米.
(1)-2=0,
∵a=1,b=-3,c=-2
∴△==17,
∴,
(2)整理得:x2﹣2x﹣3=2x﹣5,
则x2﹣4x+2=0,
(x﹣2)2=2,
解得:x1=2+,x2=2﹣,
(3)3x2﹣5x﹣2=0,
x2﹣x=,
x2﹣x+=+,
(x﹣)2=,
x﹣=±,
解得x1=﹣,x2=2;
(4)2x2﹣4x﹣1998=0,
x2﹣2x=999,
x2﹣2x+1=1000,
(x﹣1)2=1000,
x﹣1=±10,
解得x1=1﹣10,x2=1+10.
23.解:设截去的小正方形的边长为x cm,由题意得10×8-4x2=80%×10×8,
解得x1=2,x2=-2(不合题意,舍去).
所以x=2.
答:截去的小正方形的边长为2 cm.
24.解 (1)设y与x之间的函数关系式为y=kx+b,
将(22.6,34.8)、(24,32)代入y=kx+b,
,解得:,
∴y与x之间的函数关系式为y=﹣2x+80.
当x=23.5时,y=﹣2x+80=33.
答:当天该水果的销售量为33千克.
(2)根据题意得:(x﹣20)(﹣2x+80)=150,
解得:x1=35,x2=25.
∵20≤x≤32,
∴x=25.
答:如果某天销售这种水果获利150元,那么该天水果的售价为25元.
25.解:(1)∵(130 000-100 000)÷5 000=6(间),30-6=24(间),∴能租出24间.
(2)设每间商铺的年租金增加x万元,则
整理,得2x2-11x+5=0,解得x1=5,
x2=0.5,5+10=15(万元),0.5+10=10.5(万元).
∴当每间商铺的年租金定为10.5万元或15万元时,该公司的年收益为275万元.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
