2020--2021学年北师大版九年级数学下册 2.3 确定二次函数表达式 课件(共22张PPT)
文档属性
| 名称 | 2020--2021学年北师大版九年级数学下册 2.3 确定二次函数表达式 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 62.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 13:30:29 | ||
图片预览




文档简介
(共22张PPT)
北师版九年级下册 二次函数
§2.3 确定二次函数的表达式
2.能够根据问题的变化,灵活选用“一般式、顶点式、交点式”来解决二次函数表达式的相关问题.
3.在解决实际问题时,要注意灵活选用适当的坐标系来构建图象,从而
利用合适的方法解决问题.
1.经历探索“确定二次函数表达式”的过程,体会“二次函数”这一数学模型在解决实际问题中的重要意义.
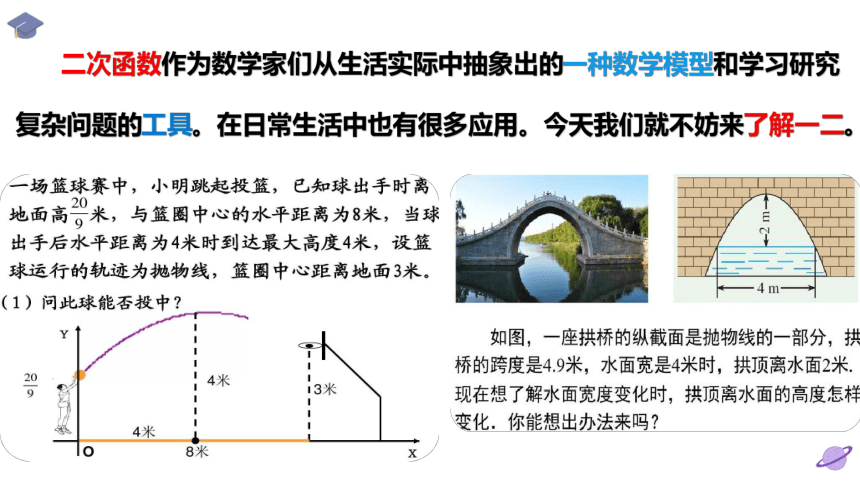
二次函数作为数学家们从生活实际中抽象出的一种数学模型和学习研究复杂问题的工具。在日常生活中也有很多应用。今天我们就不妨来了解一二。
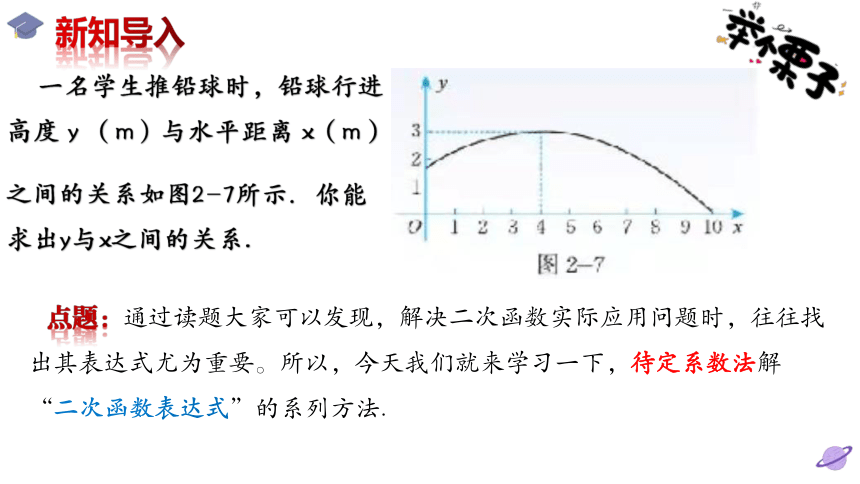
一名学生推铅球时,铅球行进高度 y (m)与水平距离 x(m)
之间的关系如图2-7所示.你能求出y与x之间的关系.
新知导入
点题:通过读题大家可以发现,解决二次函数实际应用问题时,往往找出其表达式尤为重要。所以,今天我们就来学习一下,待定系数法解“二次函数表达式”的系列方法.
知识提要:——待定系数法
解:设这个一次函数的解析式为y=kx+b,
∵一次函数图象经过点(1,3)和(-2,-12),
∴
k+b=3
-2k+b=-12
解得 k=3,b=-6
一次函数的解析式为y=3x-6.
观察右例,回顾后我们知道:
一、待定系数法解表达式的步骤:
1、设;2、代;3、列;4、解;5、列。
二、求一次函数解析式需要知道两点.
因为一次函数解析式中含有两个待定的字母——k,b。
那大家说一说,用待定系数法求二次函数解析式,里边有几个待定的字母?又需要几个已知点呢?
已知一次函数经过点(1,3)和(-2,-12),
求这个一次函数的解析式。
新知导入
问:前边我们学习了哪几类二次函数的表达形式?请大家举一下例子.
1、y=ax2;
2、y=ax2+c;
3、y=a(x-h)2;
4、y=a(x-h)2+K;
5、y=ax2+bx+c;
a≠0
一般式
顶点式
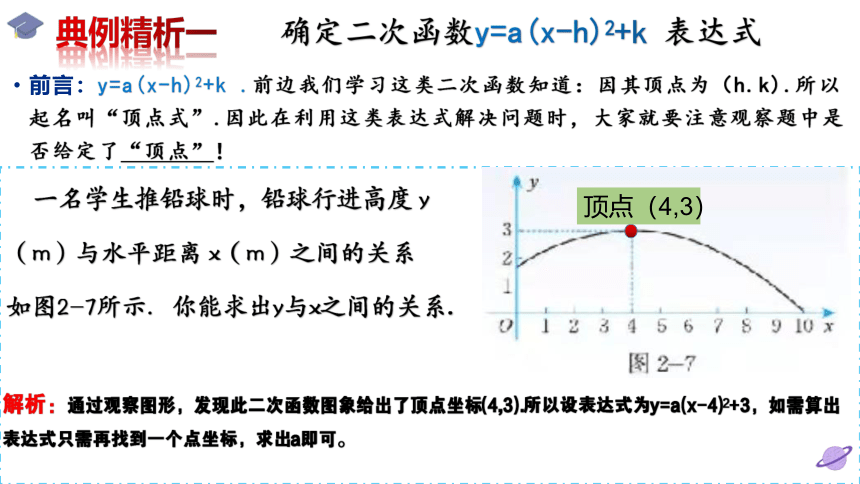
前言:y=a(x-h)2+k .前边我们学习这类二次函数知道:因其顶点为(h.k).所以起名叫“顶点式”.因此在利用这类表达式解决问题时,大家就要注意观察题中是否给定了“顶点”!
典例精析一
确定二次函数y=a(x-h)2+k 表达式
一名学生推铅球时,铅球行进高度 y
(m)与水平距离 x(m)之间的关系
如图2-7所示.你能求出y与x之间的关系.
顶点(4,3)
解析:通过观察图形,发现此二次函数图象给出了顶点坐标(4,3).所以设表达式为y=a(x-4)2+3,如需算出表达式只需再找到一个点坐标,求出a即可。
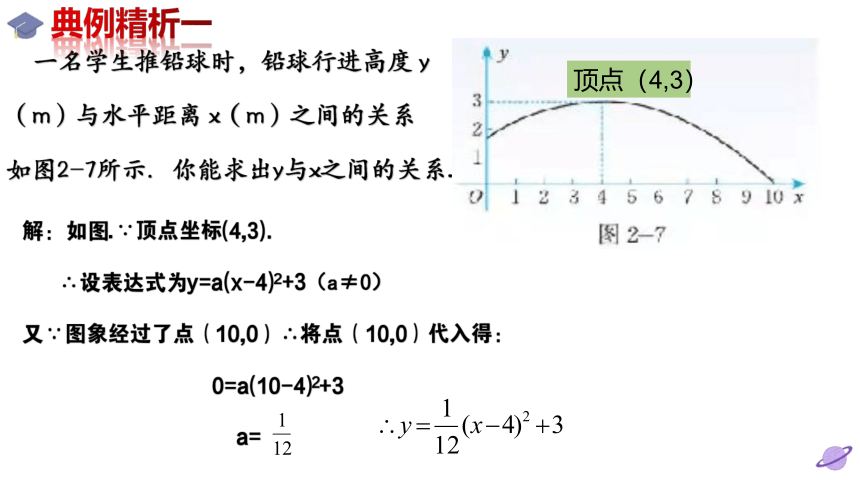
一名学生推铅球时,铅球行进高度 y
(m)与水平距离 x(m)之间的关系
如图2-7所示.你能求出y与x之间的关系.
顶点(4,3)
解:如图.∵顶点坐标(4,3).
∴设表达式为y=a(x-4)2+3(a≠0)
又∵图象经过了点(10,0)∴将点(10,0)代入得:
0=a(10-4)2+3
a=
典例精析一
小结一:二次函数表达式的解法-------顶点式算法.
1、适用于题目之中可以找到顶点坐标的问题;
2、依据顶点坐标直接设二次函数为:y=a(x-h)2+k;
3、将另一已知点代入,求出a的值;
4、列出二次函数表达式.
特别注意: 此种解法必须知道“顶点坐标”和“另一个已知点坐标”,
两个条件
已知次函数的图象与y轴交点的纵坐标为1,且经过点(2,5)和(-2,13)、求这个二次函数的表达式.
典例精析二
例
解析:本题中没有出现顶点坐标,所以可以将表达式设为y=ax2+bx+c(a≠0)
解:设二次函数为y=ax2+bx+c(a≠0)
由题意可得:图象经过(0,1)、(2,5)、(-2,13)三点.
∴将其代入得
∴y=2x2-2x+1
确定二次函数y=ax2+bx+c 表达式
1、此种解法一般适用于题中未给出“顶点坐标”;
2、设y=ax2+bx+c(a≠0);
3、找出题中三个已知点坐标代入求解;
4、利用“三元一次方程组”的解法求出a、b、c的值;
5、将a、b、c的值代入原式,列出二次函数表达式.
小结二:二次函数表达式的解法-------一般式算法.
特别注意: 一般情况下, 此种解法需要知道“三个已知点坐标”.当然,如果所给二次函数形式不完整,可根据待定字母的数量来寻找已知条件。
已知二次函数y=ax +c的图象经过点(2,3)和(-1.-3)、求这个二次函数的表达式.
跟踪练习
解∶将点(2,3)和(-1、-3)的坐标分别代入表达式y=ax +c得:
∴y=2x2+5
反思:此题适用一般式解法,且表达式中仅仅两个待定“字母”,所以仅需
两个已知点即可.
1.已知二次函数图象的顶点坐标是(-1,1),且经过点(1,-3),求这个二次函数的表达式;
2.(1)已知二次函数y=x2+bx+c的图象经过(1、1)与(2.3)两点、求这个二次函数的表达式;
跟踪练习
y=-(x+1)2+1
y=x2-x+1
1 已如二次函数图象的顶点坐标是(2,3) 且经过点(-1,0)),求这个二次函数的表达式;
2.己知二次函数图象与x轴交点的横坐标为-2和1,且经过点(0、3),求这个二次函数的表式.
合作共学
某高尔夫球手击出高尔夫球的运动路线是一条抛物线,当球水平运动了24m时,达到最高点;落球点比击球点的海拔低1m,水平距离为50m。
(1)求高度h与水平距离x的二次函数表达式;
(2)与击球点相比,球运动到最高点时有多高?
合作共学
如图,建立坐标系如下:
合作共学
解:(1)如右图,依题意可知.
图象经过(0,0)、(48,0)、(50,-1)
∴设y=ax2+bx+c(a≠0)
将以上三点代入得:
∴y=-0.01x2+0.48x
(2)如图,最高点是x=24
将x=24代入y=-0.01x2+0.48x可得
y=5.76
∴最高点5.76米.
解析:如右下图,依题意可知:此二次函数的图象与x轴有两个交点——(0,0),(48,0).采用一般式求解时,过程略微复杂,并且在今后解题过程中,常常会遇见图象与x轴的交点都已知的情况.所以,为了减少繁复的计算,我们还可以将表达式设为“y=a(x-x1)(x-x2)(其中x1,x2是图象与x轴的交点横坐标)”
拓展学习
交点式算法.
解:(1)如右图,依题意可知.
图象经过(0,0)、(48,0)∴设y=a(x-0)(x-48)
将(50,-1)代入得:
a=-0.01
∴y=-0.01x2+0.48x
已知二次函数y=ax2+bx+c的图像与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3), 求二次函数的顶点坐标.
跟踪练习
解:(1)依题意可知.
图象经过(1,0)、(3,0)∴设y=a(x-1)(x-3)
将(0,3)代入得:
a=1
∴y=x2-4x+3
注意:交点式求出以后,需要重新转化成“一般式”
有一个抛物线形的立交桥拱,这个桥拱最大高度为16m,跨度为40m.现把它的图形放在坐标系里(如图所示),求抛物线的解析式
跟踪练习
解:设抛物线的解析式为y=ax2+bx+c,
解法一:
由题意可知
抛物线经过(0,0),(20,16)和(40,0)三点
解:
根据题意可知
∵ 点(0,0)在抛物线上,
∴ 所求抛物线解析式为
本题也可选用 顶点式 来解答:
设抛物线为y=a(x-20)2+16
解法二:
根据题意可知
∵ 点(20,16)在抛物线上,
本题还可选用 交点式 来解答:
解:如右图 ,设抛物线为y=a(x-0)(x-40)
解法san:
求二次函数解析式的一般方法:
1 、已知图象上三点坐标或三对对应值,常选择一般式。
2、已知图象上顶点坐标或另一点坐标,通常选择顶点式。
3、已知图象与X轴两交点坐标,通常可选择交点式来简化计算。
课堂小结
北师版九年级下册 二次函数
§2.3 确定二次函数的表达式
2.能够根据问题的变化,灵活选用“一般式、顶点式、交点式”来解决二次函数表达式的相关问题.
3.在解决实际问题时,要注意灵活选用适当的坐标系来构建图象,从而
利用合适的方法解决问题.
1.经历探索“确定二次函数表达式”的过程,体会“二次函数”这一数学模型在解决实际问题中的重要意义.
二次函数作为数学家们从生活实际中抽象出的一种数学模型和学习研究复杂问题的工具。在日常生活中也有很多应用。今天我们就不妨来了解一二。
一名学生推铅球时,铅球行进高度 y (m)与水平距离 x(m)
之间的关系如图2-7所示.你能求出y与x之间的关系.
新知导入
点题:通过读题大家可以发现,解决二次函数实际应用问题时,往往找出其表达式尤为重要。所以,今天我们就来学习一下,待定系数法解“二次函数表达式”的系列方法.
知识提要:——待定系数法
解:设这个一次函数的解析式为y=kx+b,
∵一次函数图象经过点(1,3)和(-2,-12),
∴
k+b=3
-2k+b=-12
解得 k=3,b=-6
一次函数的解析式为y=3x-6.
观察右例,回顾后我们知道:
一、待定系数法解表达式的步骤:
1、设;2、代;3、列;4、解;5、列。
二、求一次函数解析式需要知道两点.
因为一次函数解析式中含有两个待定的字母——k,b。
那大家说一说,用待定系数法求二次函数解析式,里边有几个待定的字母?又需要几个已知点呢?
已知一次函数经过点(1,3)和(-2,-12),
求这个一次函数的解析式。
新知导入
问:前边我们学习了哪几类二次函数的表达形式?请大家举一下例子.
1、y=ax2;
2、y=ax2+c;
3、y=a(x-h)2;
4、y=a(x-h)2+K;
5、y=ax2+bx+c;
a≠0
一般式
顶点式
前言:y=a(x-h)2+k .前边我们学习这类二次函数知道:因其顶点为(h.k).所以起名叫“顶点式”.因此在利用这类表达式解决问题时,大家就要注意观察题中是否给定了“顶点”!
典例精析一
确定二次函数y=a(x-h)2+k 表达式
一名学生推铅球时,铅球行进高度 y
(m)与水平距离 x(m)之间的关系
如图2-7所示.你能求出y与x之间的关系.
顶点(4,3)
解析:通过观察图形,发现此二次函数图象给出了顶点坐标(4,3).所以设表达式为y=a(x-4)2+3,如需算出表达式只需再找到一个点坐标,求出a即可。
一名学生推铅球时,铅球行进高度 y
(m)与水平距离 x(m)之间的关系
如图2-7所示.你能求出y与x之间的关系.
顶点(4,3)
解:如图.∵顶点坐标(4,3).
∴设表达式为y=a(x-4)2+3(a≠0)
又∵图象经过了点(10,0)∴将点(10,0)代入得:
0=a(10-4)2+3
a=
典例精析一
小结一:二次函数表达式的解法-------顶点式算法.
1、适用于题目之中可以找到顶点坐标的问题;
2、依据顶点坐标直接设二次函数为:y=a(x-h)2+k;
3、将另一已知点代入,求出a的值;
4、列出二次函数表达式.
特别注意: 此种解法必须知道“顶点坐标”和“另一个已知点坐标”,
两个条件
已知次函数的图象与y轴交点的纵坐标为1,且经过点(2,5)和(-2,13)、求这个二次函数的表达式.
典例精析二
例
解析:本题中没有出现顶点坐标,所以可以将表达式设为y=ax2+bx+c(a≠0)
解:设二次函数为y=ax2+bx+c(a≠0)
由题意可得:图象经过(0,1)、(2,5)、(-2,13)三点.
∴将其代入得
∴y=2x2-2x+1
确定二次函数y=ax2+bx+c 表达式
1、此种解法一般适用于题中未给出“顶点坐标”;
2、设y=ax2+bx+c(a≠0);
3、找出题中三个已知点坐标代入求解;
4、利用“三元一次方程组”的解法求出a、b、c的值;
5、将a、b、c的值代入原式,列出二次函数表达式.
小结二:二次函数表达式的解法-------一般式算法.
特别注意: 一般情况下, 此种解法需要知道“三个已知点坐标”.当然,如果所给二次函数形式不完整,可根据待定字母的数量来寻找已知条件。
已知二次函数y=ax +c的图象经过点(2,3)和(-1.-3)、求这个二次函数的表达式.
跟踪练习
解∶将点(2,3)和(-1、-3)的坐标分别代入表达式y=ax +c得:
∴y=2x2+5
反思:此题适用一般式解法,且表达式中仅仅两个待定“字母”,所以仅需
两个已知点即可.
1.已知二次函数图象的顶点坐标是(-1,1),且经过点(1,-3),求这个二次函数的表达式;
2.(1)已知二次函数y=x2+bx+c的图象经过(1、1)与(2.3)两点、求这个二次函数的表达式;
跟踪练习
y=-(x+1)2+1
y=x2-x+1
1 已如二次函数图象的顶点坐标是(2,3) 且经过点(-1,0)),求这个二次函数的表达式;
2.己知二次函数图象与x轴交点的横坐标为-2和1,且经过点(0、3),求这个二次函数的表式.
合作共学
某高尔夫球手击出高尔夫球的运动路线是一条抛物线,当球水平运动了24m时,达到最高点;落球点比击球点的海拔低1m,水平距离为50m。
(1)求高度h与水平距离x的二次函数表达式;
(2)与击球点相比,球运动到最高点时有多高?
合作共学
如图,建立坐标系如下:
合作共学
解:(1)如右图,依题意可知.
图象经过(0,0)、(48,0)、(50,-1)
∴设y=ax2+bx+c(a≠0)
将以上三点代入得:
∴y=-0.01x2+0.48x
(2)如图,最高点是x=24
将x=24代入y=-0.01x2+0.48x可得
y=5.76
∴最高点5.76米.
解析:如右下图,依题意可知:此二次函数的图象与x轴有两个交点——(0,0),(48,0).采用一般式求解时,过程略微复杂,并且在今后解题过程中,常常会遇见图象与x轴的交点都已知的情况.所以,为了减少繁复的计算,我们还可以将表达式设为“y=a(x-x1)(x-x2)(其中x1,x2是图象与x轴的交点横坐标)”
拓展学习
交点式算法.
解:(1)如右图,依题意可知.
图象经过(0,0)、(48,0)∴设y=a(x-0)(x-48)
将(50,-1)代入得:
a=-0.01
∴y=-0.01x2+0.48x
已知二次函数y=ax2+bx+c的图像与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3), 求二次函数的顶点坐标.
跟踪练习
解:(1)依题意可知.
图象经过(1,0)、(3,0)∴设y=a(x-1)(x-3)
将(0,3)代入得:
a=1
∴y=x2-4x+3
注意:交点式求出以后,需要重新转化成“一般式”
有一个抛物线形的立交桥拱,这个桥拱最大高度为16m,跨度为40m.现把它的图形放在坐标系里(如图所示),求抛物线的解析式
跟踪练习
解:设抛物线的解析式为y=ax2+bx+c,
解法一:
由题意可知
抛物线经过(0,0),(20,16)和(40,0)三点
解:
根据题意可知
∵ 点(0,0)在抛物线上,
∴ 所求抛物线解析式为
本题也可选用 顶点式 来解答:
设抛物线为y=a(x-20)2+16
解法二:
根据题意可知
∵ 点(20,16)在抛物线上,
本题还可选用 交点式 来解答:
解:如右图 ,设抛物线为y=a(x-0)(x-40)
解法san:
求二次函数解析式的一般方法:
1 、已知图象上三点坐标或三对对应值,常选择一般式。
2、已知图象上顶点坐标或另一点坐标,通常选择顶点式。
3、已知图象与X轴两交点坐标,通常可选择交点式来简化计算。
课堂小结
