北师大版八年级数学上册 第三章 位置与坐标回顾与思考课件(共28张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 第三章 位置与坐标回顾与思考课件(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 13:44:04 | ||
图片预览








文档简介
(共28张PPT)
位置与坐标
回顾与思考
分析生活中确定位置的方法
总结平面内确定位置的规律
确定位置的方式及极坐标思想
平面直角坐标系的基本概念
各类点的坐标特点
轴对称与坐标之间的关系
位置与坐标
知识梳理问题
1.在平面内,确定点的位置一般需要几个数据?举例说明。
2.平面直角坐标系中,如何确定给定点的坐标?给定坐标,如何确定对应的点?分别举例说明。
3.平面直角坐标系中,坐标轴上的点具有什么特点?平行于坐标轴的线段上的点,它们的坐标之间有什么样的关系?分别举例说明。
知识梳理问题
4.平面直角坐标系中,关于坐标轴对称的点的坐标之间具有怎样的关系?反过来坐标具有这样的关系的点关于坐标轴对称吗?这些结论可以帮助你解决哪些问题?
5.通过上述知识的回顾,请你整理出本章的知识框架图:
一、确定平面上点的位置
的常用方法
1.如图,A、B、C是棋子在方格纸上摆出的三个位置,如果用(2,5)表示A的位置,则B表示为_________,C表示为_________。
2.如图是灯塔A的方位图,A的位置需要_____个数据来确定,它们是____________________ 。
A
B C
A
东
30°
0
2km
北
(一)确定平面上点的位置的常用方法
(1,4)
(4,4)
两
(方位角,A与O点的距离)
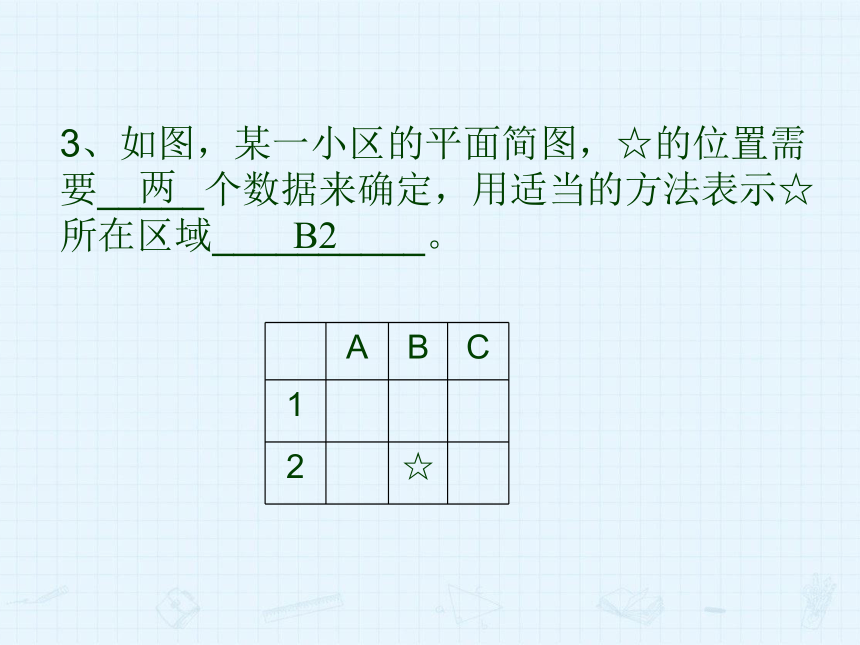
3、如图,某一小区的平面简图,☆的位置需要_____个数据来确定,用适当的方法表示☆所在区域__________。
A B C
1
2 ☆
两
B2
二、平面直角坐标系中点
的坐标特征
(二)平面直角坐标系中点的坐标特征
1.象限内点的坐标特征
点 P(x,-y)在第三象限,则Q(-x,y3 )在第______象限.
2.坐标轴上的点的坐标特征
已知点M(2+x,9-x2 )在x轴的负半轴上,则点M的坐标是 ;
3.平行坐标轴的直线上的点的坐标特征
已知线段AB平行于x轴,若点A的坐标为(-2,3),线段AB的长为5,则点B的坐标是 。
一
(-1,0)
(-7,3)或(3,3)
4. 对称点的坐标特征
点P(1,2)关于x轴对称的点的坐标是______ ,
点P(1,2)关 于原点对称的点的坐标是_______ ;
5. 象限角的平分线上的点的坐标特征
已知点P(a+3,7+a)位于二、四象限的角平分线上,则a=_______.
(1,-2)
(-1,-2)
-5
课堂练习
1. 已知平面内一点p,它的横坐标与纵坐标互为相反数,且与原点的距离为2,则点p坐标为( ).
(A)(-1,1)或(1,-1) (B)(1,-1)
(C)(- , )或( ,- ) (D)( ,- )
2. 一个点在y轴上,距原点的距离是6,则这个点的坐标是 。
C
(0,6)或(0,-6)
3.已知点M在y轴上,点P(3,-2),若线段MP的长为5,则点M的是 。
4.正△ABC的顶点A,B的坐标分别为A(0,0),B(2,0)则C点的坐标为 ;
5.将A( ,2)的坐标乘以-1得点B,则线段AB的长为________.
6.已知点A(4,y),B(x,-3),如果AB//x轴,且线段AB的长为5,则x的值为________,y的值为_____。
8
-1或9
-3
(0,-6)或(0,2)
三、图形的轴对称变换
(三)图形的轴对称变换
1. 将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系。
(1)纵坐标不变,横坐标乘以-1 ;
(2)横坐标不变.纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
1. 将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系。
(1)纵坐标不变,横坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
解:
图形变化前后点的坐标分别为:
(-5,4)
(-8,2)
(-7,2)
(-3,2)
(-2,2)
(-7,0)
(-3,0)
变化后
(5,4)
(8,2)
(7,2)
(3,2)
(2,2)
(7,0)
(3,0)
变化前
所得图形与原图形关于y轴对称.
(2)横坐标不变,纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
解:
图形变化前后点的坐标分别为:
变化前 (3,0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (3,0) (7,0) (2,-2) (3,-2) (7,-2) (8,-2) (5,-4)
-1
-2
-3
-4
所得图形与原图形关于x轴对称.
四、求点的坐标
X
Y
1
2
3
4
3
1
4
2
5
5
0
·
M(4,3)
4个单位长度
3个单位长度
点的坐标与点到坐标轴的距离关系
注意:点到坐标轴的距离是点的横纵坐标的绝对值
点P(x,y)到x轴的距离是IyI,到y轴的距离是IxI。
1.(1)如果点p在直角坐标系中到x轴的距离为2,到y轴的距离为3,则点p的坐标是 。
(2)已知点A(0,2),B(4,1),点P是x轴上的一点,则PA+PB的最小值是 。
(3,2)或(3,-2)或(-3,2)或(-3,-2)
5
(3)如图所示,在平面直角坐标系中,菱形MNPO的顶点P坐标是(3,4),则顶点M、N的坐标分别是 。
M(5,0),N(8,4)
(3,4)
E
F
(4)正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),则C点的坐标________.
证△ABO≌△BCE
E
(1,-3)
2.如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
(2,4)或(8,4)或(3,4)
P1
P3
P2
(1)以D为圆心,OD长(长为5)为半径画弧交BC于P1、P2点
(2)以O为圆心,OD长(长为5)为半径画弧交BC于P3点
3.已知点A(2,1),O(0,0),请你在数轴上确定点P,使得△AOP成为等腰三角形,写出所有存在的点P的坐标。
O
x
A
y
1.等边三角形的两个顶点的坐标分别为
(-4,0),(4,0),则第三个顶点的坐标为 。
2.菱形的边长为6,一个内角为120度,以对角线的交点为坐标原点建立坐标系,且较长的对角线与x轴重合,则菱形各顶点的坐标为 。
练习
3.在如图所示的平面直角坐标系中,圆的圆心
P的坐标为(2,0),圆的半径为3,求圆与坐标轴的交点A,B,C,D的坐标.
0
x
y
A
B
C
D
P
4.梯形ABCD中,AB=CD=DA=3,BC=5,求点A,D的坐标.
0
x
y
A
B
C
D
回顾与小结:
1.确定位置的方法:
(1)坐标定位法;
(2)方位角+距离;
(3)区域定位法.
2.平面直角坐标系
3.图形轴对称的关系
关于平面直角坐标系,你还学会了哪些 说说看
你说,我说,大家说
位置与坐标
回顾与思考
分析生活中确定位置的方法
总结平面内确定位置的规律
确定位置的方式及极坐标思想
平面直角坐标系的基本概念
各类点的坐标特点
轴对称与坐标之间的关系
位置与坐标
知识梳理问题
1.在平面内,确定点的位置一般需要几个数据?举例说明。
2.平面直角坐标系中,如何确定给定点的坐标?给定坐标,如何确定对应的点?分别举例说明。
3.平面直角坐标系中,坐标轴上的点具有什么特点?平行于坐标轴的线段上的点,它们的坐标之间有什么样的关系?分别举例说明。
知识梳理问题
4.平面直角坐标系中,关于坐标轴对称的点的坐标之间具有怎样的关系?反过来坐标具有这样的关系的点关于坐标轴对称吗?这些结论可以帮助你解决哪些问题?
5.通过上述知识的回顾,请你整理出本章的知识框架图:
一、确定平面上点的位置
的常用方法
1.如图,A、B、C是棋子在方格纸上摆出的三个位置,如果用(2,5)表示A的位置,则B表示为_________,C表示为_________。
2.如图是灯塔A的方位图,A的位置需要_____个数据来确定,它们是____________________ 。
A
B C
A
东
30°
0
2km
北
(一)确定平面上点的位置的常用方法
(1,4)
(4,4)
两
(方位角,A与O点的距离)
3、如图,某一小区的平面简图,☆的位置需要_____个数据来确定,用适当的方法表示☆所在区域__________。
A B C
1
2 ☆
两
B2
二、平面直角坐标系中点
的坐标特征
(二)平面直角坐标系中点的坐标特征
1.象限内点的坐标特征
点 P(x,-y)在第三象限,则Q(-x,y3 )在第______象限.
2.坐标轴上的点的坐标特征
已知点M(2+x,9-x2 )在x轴的负半轴上,则点M的坐标是 ;
3.平行坐标轴的直线上的点的坐标特征
已知线段AB平行于x轴,若点A的坐标为(-2,3),线段AB的长为5,则点B的坐标是 。
一
(-1,0)
(-7,3)或(3,3)
4. 对称点的坐标特征
点P(1,2)关于x轴对称的点的坐标是______ ,
点P(1,2)关 于原点对称的点的坐标是_______ ;
5. 象限角的平分线上的点的坐标特征
已知点P(a+3,7+a)位于二、四象限的角平分线上,则a=_______.
(1,-2)
(-1,-2)
-5
课堂练习
1. 已知平面内一点p,它的横坐标与纵坐标互为相反数,且与原点的距离为2,则点p坐标为( ).
(A)(-1,1)或(1,-1) (B)(1,-1)
(C)(- , )或( ,- ) (D)( ,- )
2. 一个点在y轴上,距原点的距离是6,则这个点的坐标是 。
C
(0,6)或(0,-6)
3.已知点M在y轴上,点P(3,-2),若线段MP的长为5,则点M的是 。
4.正△ABC的顶点A,B的坐标分别为A(0,0),B(2,0)则C点的坐标为 ;
5.将A( ,2)的坐标乘以-1得点B,则线段AB的长为________.
6.已知点A(4,y),B(x,-3),如果AB//x轴,且线段AB的长为5,则x的值为________,y的值为_____。
8
-1或9
-3
(0,-6)或(0,2)
三、图形的轴对称变换
(三)图形的轴对称变换
1. 将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系。
(1)纵坐标不变,横坐标乘以-1 ;
(2)横坐标不变.纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
1. 将图中的点(3,0),(7,0),(2,2)(3,2),(7,2),(8,2),(5,4)做如下变化,画出图形,说说变化前后图形的关系。
(1)纵坐标不变,横坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
解:
图形变化前后点的坐标分别为:
(-5,4)
(-8,2)
(-7,2)
(-3,2)
(-2,2)
(-7,0)
(-3,0)
变化后
(5,4)
(8,2)
(7,2)
(3,2)
(2,2)
(7,0)
(3,0)
变化前
所得图形与原图形关于y轴对称.
(2)横坐标不变,纵坐标分别乘以-1.
2 3 4 5 6 7 8
3
2
4
5
解:
图形变化前后点的坐标分别为:
变化前 (3,0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4)
变化后 (3,0) (7,0) (2,-2) (3,-2) (7,-2) (8,-2) (5,-4)
-1
-2
-3
-4
所得图形与原图形关于x轴对称.
四、求点的坐标
X
Y
1
2
3
4
3
1
4
2
5
5
0
·
M(4,3)
4个单位长度
3个单位长度
点的坐标与点到坐标轴的距离关系
注意:点到坐标轴的距离是点的横纵坐标的绝对值
点P(x,y)到x轴的距离是IyI,到y轴的距离是IxI。
1.(1)如果点p在直角坐标系中到x轴的距离为2,到y轴的距离为3,则点p的坐标是 。
(2)已知点A(0,2),B(4,1),点P是x轴上的一点,则PA+PB的最小值是 。
(3,2)或(3,-2)或(-3,2)或(-3,-2)
5
(3)如图所示,在平面直角坐标系中,菱形MNPO的顶点P坐标是(3,4),则顶点M、N的坐标分别是 。
M(5,0),N(8,4)
(3,4)
E
F
(4)正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),则C点的坐标________.
证△ABO≌△BCE
E
(1,-3)
2.如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
(2,4)或(8,4)或(3,4)
P1
P3
P2
(1)以D为圆心,OD长(长为5)为半径画弧交BC于P1、P2点
(2)以O为圆心,OD长(长为5)为半径画弧交BC于P3点
3.已知点A(2,1),O(0,0),请你在数轴上确定点P,使得△AOP成为等腰三角形,写出所有存在的点P的坐标。
O
x
A
y
1.等边三角形的两个顶点的坐标分别为
(-4,0),(4,0),则第三个顶点的坐标为 。
2.菱形的边长为6,一个内角为120度,以对角线的交点为坐标原点建立坐标系,且较长的对角线与x轴重合,则菱形各顶点的坐标为 。
练习
3.在如图所示的平面直角坐标系中,圆的圆心
P的坐标为(2,0),圆的半径为3,求圆与坐标轴的交点A,B,C,D的坐标.
0
x
y
A
B
C
D
P
4.梯形ABCD中,AB=CD=DA=3,BC=5,求点A,D的坐标.
0
x
y
A
B
C
D
回顾与小结:
1.确定位置的方法:
(1)坐标定位法;
(2)方位角+距离;
(3)区域定位法.
2.平面直角坐标系
3.图形轴对称的关系
关于平面直角坐标系,你还学会了哪些 说说看
你说,我说,大家说
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
