北师大版八年级数学上册 1.1 探索勾股定理 (2)课件(共19张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 1.1 探索勾股定理 (2)课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 14:33:55 | ||
图片预览

文档简介
(共19张PPT)
勾股定理的应用
最短路线问题
北师大版八年级上册
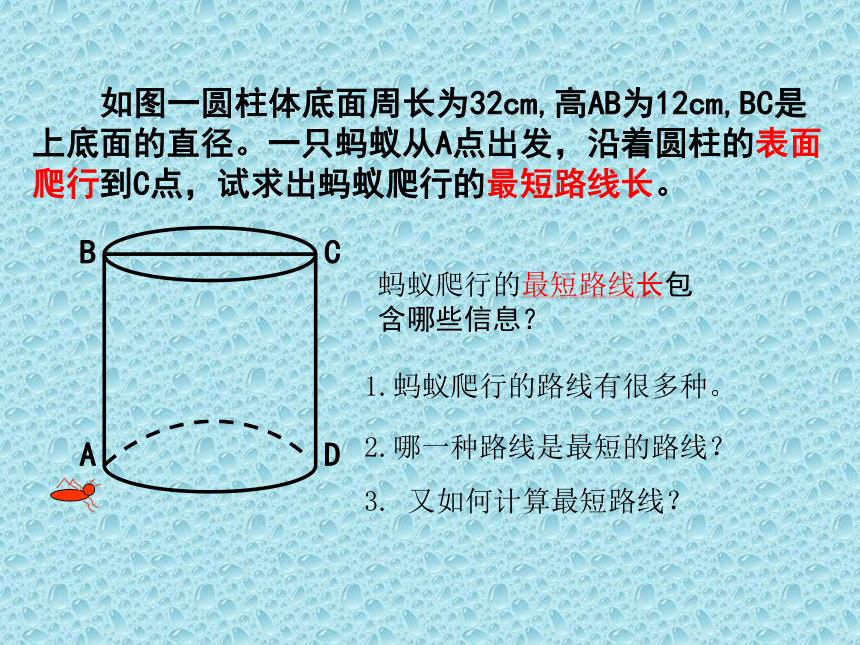
如图一圆柱体底面周长为32cm,高AB为12cm,BC是
上底面的直径。一只蚂蚁从A点出发,沿着圆柱的表面
爬行到C点,试求出蚂蚁爬行的最短路线长。
A
B
D
C
蚂蚁爬行的最短路线长包含哪些信息?
1.蚂蚁爬行的路线有很多种。
2.哪一种路线是最短的路线?
3. 又如何计算最短路线?
B
C
A
d
B
C
A
d
C
A
d
B
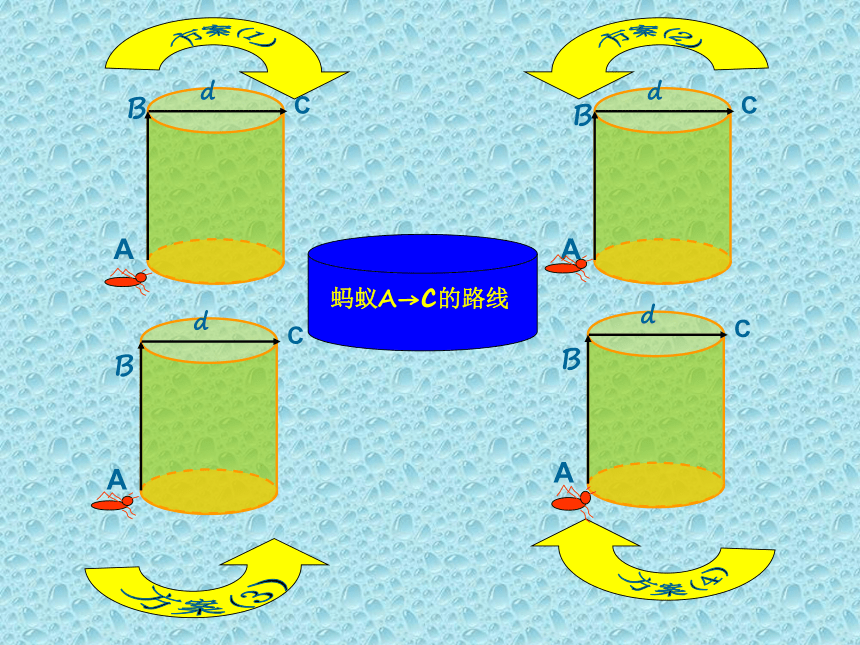
蚂蚁A→c的路线
C
A
B
d
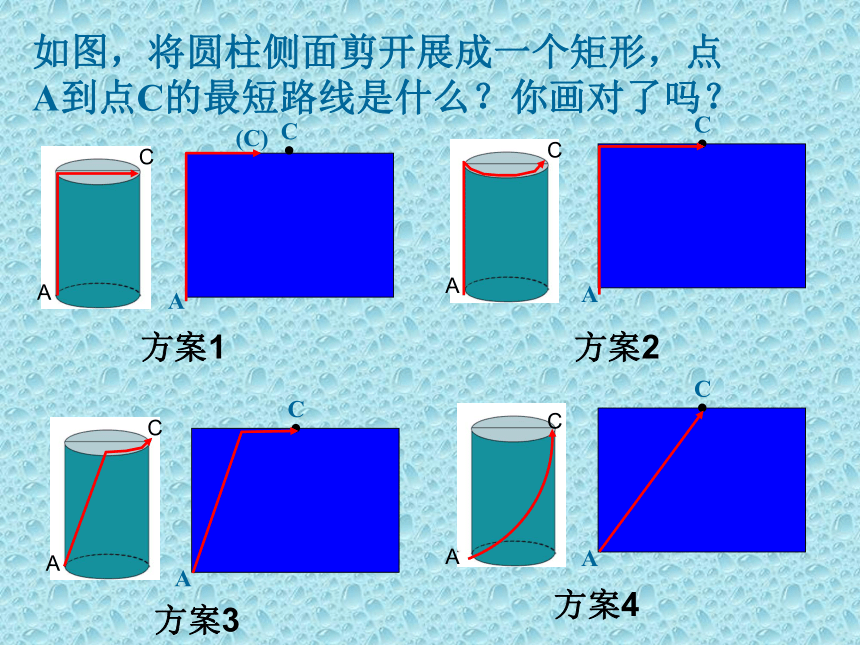
如图,将圆柱侧面剪开展成一个矩形,点
A到点C的最短路线是什么?你画对了吗?
A
C
(C)
A
C
A
C
A
C
方案1
方案2
方案4
方案3
C
A
C
A
C
A
C
A
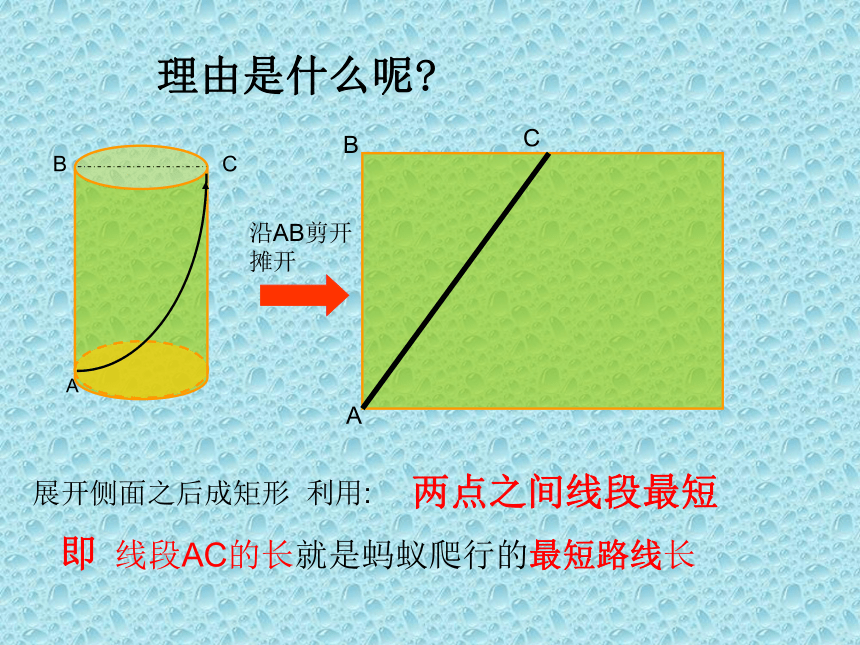
理由是什么呢
A
C
B
A
C
展开侧面之后成矩形 利用:
B
沿AB剪开 摊开
两点之间线段最短
即 线段AC的长就是蚂蚁爬行的最短路线长
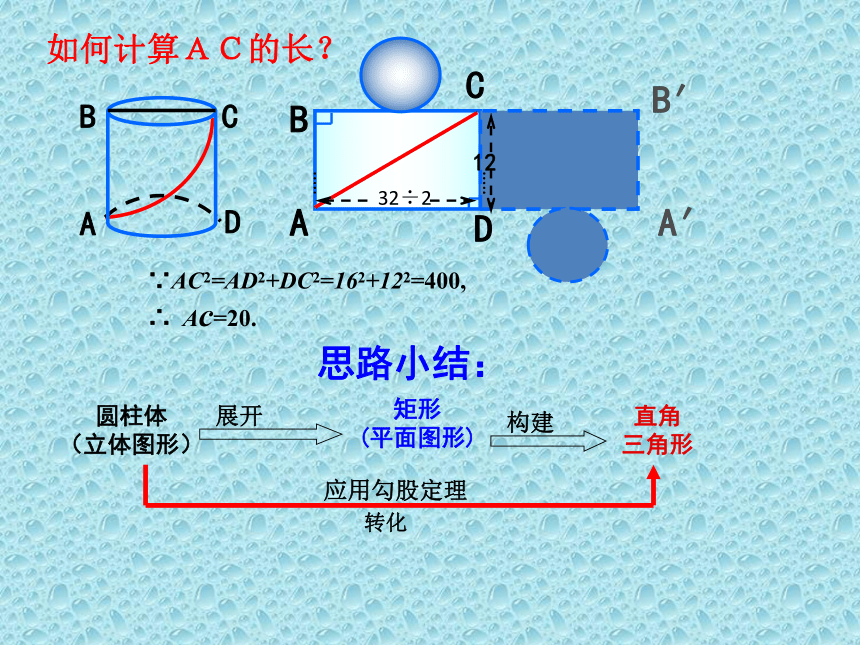
思路小结:
圆柱体
(立体图形)
矩形
(平面图形)
直角
三角形
展开
构建
转化
应用勾股定理
A
B
D
C
B
A
C
D
B′
A′
12
∵AC2=AD2+DC2=162+122=400,
∴ Ac=20.
32÷2
如何计算AC的长?
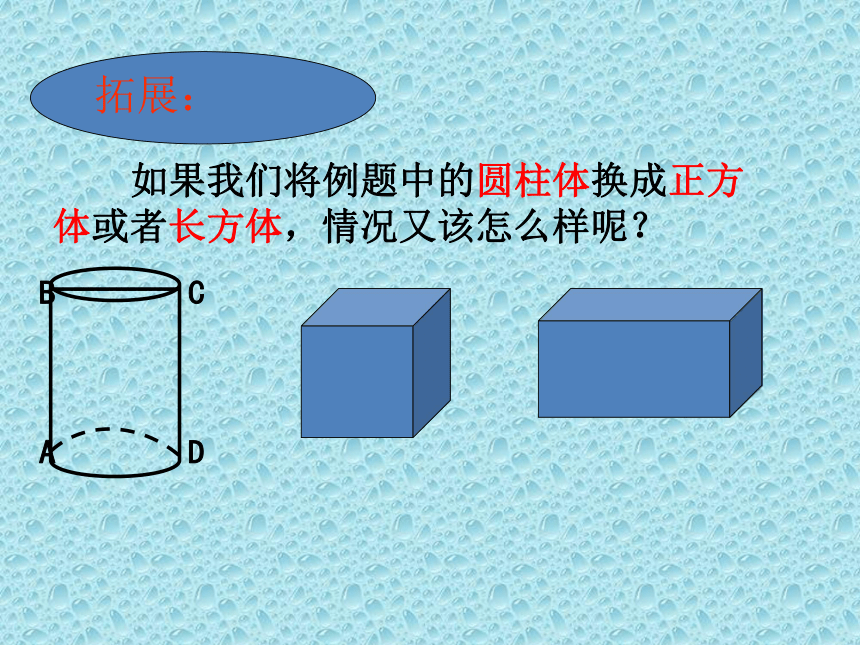
如果我们将例题中的圆柱体换成正方体或者长方体,情况又该怎么样呢?
拓展:
A
B
D
C
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面从A点爬行到B点的最短路线长又是多少呢?
A
B
B
A
B′
两条线路,看明白了吗
即 1、展 -----
(立体 平面)
起点A,终点B或B′
最短路线AB和AB ′
利用勾股定理
2、找------
3、连------
4、算------
A
B
A
B
10
10
10
B
C
A
总结: 展开任意两个面
( 因为每个面都一样)
∵ AB2=AC2+BC2=202+102=500
∴ AB=
如果正方体盒子换成长为4cm,宽为2cm,高为1cm的长方体盒子,蚂蚁沿着表面从A点爬行到B点的最短路线长又是多少呢?
A
B
线段AB是起点和终点所在的并且是相邻的两个平面图形所组成的矩形的对角线。
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
即起点和终点所在的并且是相邻的两个平面图形所组成的矩形会有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
A
B
2
4
A
B
1
C
4
2
1
B
D
A
4
2
1
B
E
A
C
D
E
F
G
H
蚂蚁沿着长方体表面从注爬到B的最短距离的平方分别是:
总结提升
给出一个长方体,设它的长、宽、高分别是a、b、c,且a你能用上述方法快速计算下面这只蚂蚁要爬行的距离吗?
1.如图,正方体的所有而是由3x3个边长为1cm的小正方形组成.蚂蚁从底而A出沿着表而爬到右侧点B处,至少要爬行 cm.
挑战自我
2.如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
∵ AB2=AC2+BC2=625,
∴ AB=25 dm
挑战自我
3.如图,一圆柱高9cm,底面半径2cm,一只蚂蚁从距上底面1厘米点A爬到对角B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
A
A
B
C
挑战自我
4.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离的平方是多少?
10
20
B
A
C
15
5
挑战自我
10
20
B
5
F
E
10
20
A
C
F
B
5
10
20
A
C
E
10
A
E
C
B
20
15
5
你学会了怎样的解题思路?
实际问题
数学问题
转化
直角三角形
课后反思
构建
勾股定理
应用
勾股定理的应用
最短路线问题
北师大版八年级上册
如图一圆柱体底面周长为32cm,高AB为12cm,BC是
上底面的直径。一只蚂蚁从A点出发,沿着圆柱的表面
爬行到C点,试求出蚂蚁爬行的最短路线长。
A
B
D
C
蚂蚁爬行的最短路线长包含哪些信息?
1.蚂蚁爬行的路线有很多种。
2.哪一种路线是最短的路线?
3. 又如何计算最短路线?
B
C
A
d
B
C
A
d
C
A
d
B
蚂蚁A→c的路线
C
A
B
d
如图,将圆柱侧面剪开展成一个矩形,点
A到点C的最短路线是什么?你画对了吗?
A
C
(C)
A
C
A
C
A
C
方案1
方案2
方案4
方案3
C
A
C
A
C
A
C
A
理由是什么呢
A
C
B
A
C
展开侧面之后成矩形 利用:
B
沿AB剪开 摊开
两点之间线段最短
即 线段AC的长就是蚂蚁爬行的最短路线长
思路小结:
圆柱体
(立体图形)
矩形
(平面图形)
直角
三角形
展开
构建
转化
应用勾股定理
A
B
D
C
B
A
C
D
B′
A′
12
∵AC2=AD2+DC2=162+122=400,
∴ Ac=20.
32÷2
如何计算AC的长?
如果我们将例题中的圆柱体换成正方体或者长方体,情况又该怎么样呢?
拓展:
A
B
D
C
如果圆柱换成如图的棱长为10cm的正方体盒子,蚂蚁沿着表面从A点爬行到B点的最短路线长又是多少呢?
A
B
B
A
B′
两条线路,看明白了吗
即 1、展 -----
(立体 平面)
起点A,终点B或B′
最短路线AB和AB ′
利用勾股定理
2、找------
3、连------
4、算------
A
B
A
B
10
10
10
B
C
A
总结: 展开任意两个面
( 因为每个面都一样)
∵ AB2=AC2+BC2=202+102=500
∴ AB=
如果正方体盒子换成长为4cm,宽为2cm,高为1cm的长方体盒子,蚂蚁沿着表面从A点爬行到B点的最短路线长又是多少呢?
A
B
线段AB是起点和终点所在的并且是相邻的两个平面图形所组成的矩形的对角线。
分析:蚂蚁由A爬到B过程中较短的路线有多少种情况?
即起点和终点所在的并且是相邻的两个平面图形所组成的矩形会有多少种情况?
(1)经过前面和上底面;
(2)经过前面和右面;
(3)经过左面和上底面.
A
B
2
4
A
B
1
C
4
2
1
B
D
A
4
2
1
B
E
A
C
D
E
F
G
H
蚂蚁沿着长方体表面从注爬到B的最短距离的平方分别是:
总结提升
给出一个长方体,设它的长、宽、高分别是a、b、c,且a
1.如图,正方体的所有而是由3x3个边长为1cm的小正方形组成.蚂蚁从底而A出沿着表而爬到右侧点B处,至少要爬行 cm.
挑战自我
2.如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
∵ AB2=AC2+BC2=625,
∴ AB=25 dm
挑战自我
3.如图,一圆柱高9cm,底面半径2cm,一只蚂蚁从距上底面1厘米点A爬到对角B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
A
A
B
C
挑战自我
4.如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离的平方是多少?
10
20
B
A
C
15
5
挑战自我
10
20
B
5
F
E
10
20
A
C
F
B
5
10
20
A
C
E
10
A
E
C
B
20
15
5
你学会了怎样的解题思路?
实际问题
数学问题
转化
直角三角形
课后反思
构建
勾股定理
应用
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
