2.4.1 面积最大问题 课件(共18张PPT)
文档属性
| 名称 | 2.4.1 面积最大问题 课件(共18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 61.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览




文档简介
(共18张PPT)
北师版九年级下册 二次函数
§2.4.1 二次函数的应用
——面积最大及其它
2.掌握有关平面图形中的面积最大值的解题方法.
3.学会通过建立适当的直角坐标系,来解决一些实际问题.
1.通过对两类应用问题的探究和学习,培养学生的数学建模意识和能力.
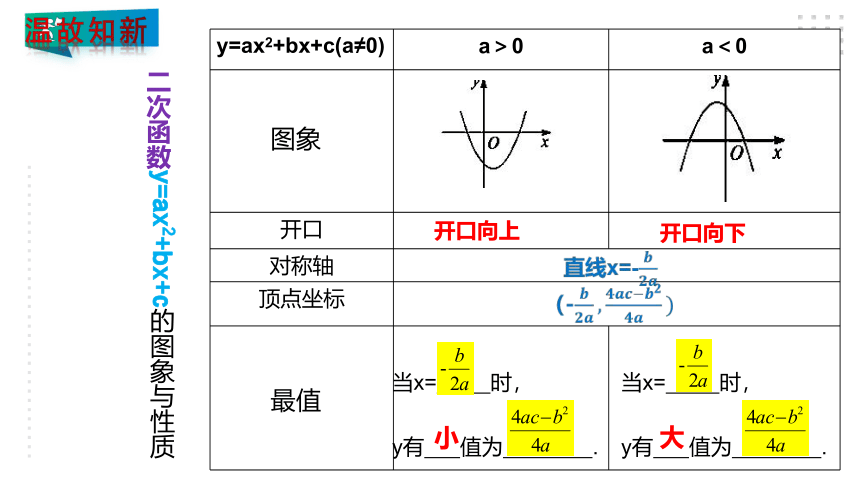
y=ax2+bx+c(a≠0) a>0 a<0
开口
对称轴 顶点坐标
图象
最值
当x= 时,
y有 值为 .
当x= 时,
y有 值为 .
开口向上
开口向下
小
大
二次函数y=ax2+bx+c的图象与性质
温故知新
典例精析一
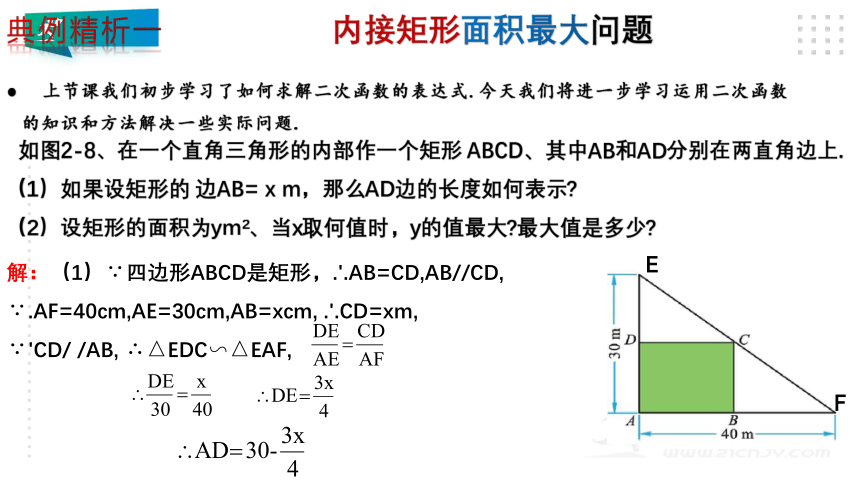
上节课我们初步学习了如何求解二次函数的表达式.今天我们将进一步学习运用二次函数的知识和方法解决一些实际问题.
如图2-8、在一个直角三角形的内部作一个矩形 ABCD、其中AB和AD分别在两直角边上.
(1)如果设矩形的 边AB= x m,那么AD边的长度如何表示
(2)设矩形的面积为ym 、当x取何值时,y的值最大 最大值是多少
内接矩形面积最大问题
解:(1)∵四边形ABCD是矩形,.'.AB=CD,AB//CD,
∵.AF=40cm,AE=30cm,AB=xcm, .'.CD=xm,
∵'CD/ /AB, ∴△EDC∽△EAF,
E
F
(2)矩形的面积∶
S=AB×AD=x(30-x)=-x2+30x(0E
F
典例精析一
内接矩形面积最大问题
在上面的问题中,如果把矩形改为如图所示的位置。其他条件不变,那么矩形的最大
面积是多少 你是怎样知道的
合作共学
解:如图所示,过点、E作EM⊥GF,交DA于点N,交 CB于点M. ∵DA// CB、EN⊥DA.
设矩形的宽是xm,面积是ym . ∵DA //GF,
.
∴EM=24m
在Rt△GEF中,
由勾股定理得 GF= 50(m)
因此,矩形的最大面积是 300m2.
内接矩形面积最大问题
小结一:
一、利用二次函数的方法解决面积(或其它)最大值问题的步骤:
1、结合题目所给条件,借助三角形相似的方式,构建二次函数的计算模型;
2、最大值计算模式:
二、通过对比两个问题的结论,我们可以发现一个猜想:
直角三角形内接矩形(各顶点均在三角形边上)面积最大值=直角三角形面积的一半;
合作共学
例:在锐角三角形ABC中,AB=12,BC=10,AC=8,BC边上的高AN=6,四边形 DEFG是矩形,求矩形面积的最大值.
在锐角三角形中截一个面积最大的正方形,
解:如图, ∵DG// CB、AN⊥BC.交DG于点M.
设矩形的宽是x,面积是y. ∵DA //GF,
.
∵DE =MN=x,∴AM=6-x
.
∴矩形面积的最大值是30.
(2)矩形的一边落在BC边上时(如图1).
(3)矩形的一边落在AC边上时(如图2).
通过对第一种情况的解答,可以初步验证“猜想”依然成立。不过,
锐角三角形的内接矩形还有另两种情况,这个留做作业,课下完成.
通过对“直角三角形内接矩形”、“锐角三角形内接矩形”面积最大值问题的讨论,
我们学习和了解到了:
一、涉及二次函数求其最大值的基本方法;
二、“猜想”——“任意已知三角形内接矩形”的面积最大值等于三角形面积的一半.
小结二:
除以上情况之外,在其它特定的图形中的内接矩形面积最大值是否也有这种规律呢?如果不是,又会有什么不同的规律呢?
如图,已知 OPQ是半径为1,圆心角为的扇形,C是扇形弧QPC上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形 ABCD的面积最大 并求出这个最大面积.
注意:本题是涉及高中数学知识的一道题目,不过所用到的方法大部分还是初中的内容。有兴趣的
同学可以想一想。
1、一根铝合金型材长为6m,用它制作一个“日”字型的窗框,如果恰好用完这根铝合金型材,那么窗架的长宽各为多少米时,窗架的面积最大?
课堂练习
答案:长为1.5米,宽为1米时,窗框的面积最大.
2、小亮父亲想用长80m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知外墙长为50m,设矩形 ABCD的边 AB=xm,面积为Sm
(1)写出S与x之间的关系式、并指出x的取值范围;
(2)当 AB,BC分别为多少求时,羊圈的面积最大 最大面积是多少
课堂练习
答案:(1)S= -2x2+80x(15≤x≤40);
(2)AB=20m,BC=40m时,羊圈面积最大,最大为800m2
【例】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)按如图所示的直角坐标系,求此抛物线的函数表达式;
合作共学
解:设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,设点B(10,n),点D(5,n+3),
由题意:
(2)有-条船以5km/h的速度向此桥径直驶来,当船距离此桥35km时.桥下水位正好在AB处.之后水位每小时上涨0.25m.当水位达到CD处时.将禁止船只通行,如果该船的速度不变,那么它能否安全通过此桥
解:由题意得:船行驶到桥下的时间为:35÷5=7小时,
水位上升的高度为:0.25×7=1.75米.
∵1.75<3
∴船的速度不变,它能安全通过此桥.
合作共学
如图,隧道的截面由抛物线和长方形构成,长方形的长为8m,宽是2m。可抛物线可以用y=-x2+4表示.
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗
(2)如果该隧道内设双向行车道,那么这辆货运卡车是可以通过
跟踪练习
(1)解:
当x=1时,y=3.75,
∵3.75+2=5.75>4,
∴能通过
(2)
当x=2时,y=3,
∵3+2=5.7>4,
∴该隧道设双向车道,这辆车也能通过.
(2010内蒙呼和浩特)如图①是抛物线形拱桥,当水面在n时,拱顶离水面2米,水面宽4米.若水面下降1米,则水面宽度将增加多少米?
跟踪练习
A
B
O
C
D
X
Y
解:按如左图所示的直角坐标系,设抛物线为y=ax2
由题意得:C(-2,-2)、D(2,-2),A,B两点
的纵坐标均为-3.
将C(-2,-2)代入y=ax2得,a=-0.5
∴y=-0.5x2
∴将y=-3代入y=-0.5x2得 x=±√6
∴AB=2√6
∴增加了AB-CD=(2√6-4)米
一、通过利用现实情景或者纯数学情景,培养学生的数学建模能力和应用意识。
它的基本思路是:
课堂小结
二、运用二次函数求最大值的基本模式:
北师版九年级下册 二次函数
§2.4.1 二次函数的应用
——面积最大及其它
2.掌握有关平面图形中的面积最大值的解题方法.
3.学会通过建立适当的直角坐标系,来解决一些实际问题.
1.通过对两类应用问题的探究和学习,培养学生的数学建模意识和能力.
y=ax2+bx+c(a≠0) a>0 a<0
开口
对称轴 顶点坐标
图象
最值
当x= 时,
y有 值为 .
当x= 时,
y有 值为 .
开口向上
开口向下
小
大
二次函数y=ax2+bx+c的图象与性质
温故知新
典例精析一
上节课我们初步学习了如何求解二次函数的表达式.今天我们将进一步学习运用二次函数的知识和方法解决一些实际问题.
如图2-8、在一个直角三角形的内部作一个矩形 ABCD、其中AB和AD分别在两直角边上.
(1)如果设矩形的 边AB= x m,那么AD边的长度如何表示
(2)设矩形的面积为ym 、当x取何值时,y的值最大 最大值是多少
内接矩形面积最大问题
解:(1)∵四边形ABCD是矩形,.'.AB=CD,AB//CD,
∵.AF=40cm,AE=30cm,AB=xcm, .'.CD=xm,
∵'CD/ /AB, ∴△EDC∽△EAF,
E
F
(2)矩形的面积∶
S=AB×AD=x(30-x)=-x2+30x(0
F
典例精析一
内接矩形面积最大问题
在上面的问题中,如果把矩形改为如图所示的位置。其他条件不变,那么矩形的最大
面积是多少 你是怎样知道的
合作共学
解:如图所示,过点、E作EM⊥GF,交DA于点N,交 CB于点M. ∵DA// CB、EN⊥DA.
设矩形的宽是xm,面积是ym . ∵DA //GF,
.
∴EM=24m
在Rt△GEF中,
由勾股定理得 GF= 50(m)
因此,矩形的最大面积是 300m2.
内接矩形面积最大问题
小结一:
一、利用二次函数的方法解决面积(或其它)最大值问题的步骤:
1、结合题目所给条件,借助三角形相似的方式,构建二次函数的计算模型;
2、最大值计算模式:
二、通过对比两个问题的结论,我们可以发现一个猜想:
直角三角形内接矩形(各顶点均在三角形边上)面积最大值=直角三角形面积的一半;
合作共学
例:在锐角三角形ABC中,AB=12,BC=10,AC=8,BC边上的高AN=6,四边形 DEFG是矩形,求矩形面积的最大值.
在锐角三角形中截一个面积最大的正方形,
解:如图, ∵DG// CB、AN⊥BC.交DG于点M.
设矩形的宽是x,面积是y. ∵DA //GF,
.
∵DE =MN=x,∴AM=6-x
.
∴矩形面积的最大值是30.
(2)矩形的一边落在BC边上时(如图1).
(3)矩形的一边落在AC边上时(如图2).
通过对第一种情况的解答,可以初步验证“猜想”依然成立。不过,
锐角三角形的内接矩形还有另两种情况,这个留做作业,课下完成.
通过对“直角三角形内接矩形”、“锐角三角形内接矩形”面积最大值问题的讨论,
我们学习和了解到了:
一、涉及二次函数求其最大值的基本方法;
二、“猜想”——“任意已知三角形内接矩形”的面积最大值等于三角形面积的一半.
小结二:
除以上情况之外,在其它特定的图形中的内接矩形面积最大值是否也有这种规律呢?如果不是,又会有什么不同的规律呢?
如图,已知 OPQ是半径为1,圆心角为的扇形,C是扇形弧QPC上的动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形 ABCD的面积最大 并求出这个最大面积.
注意:本题是涉及高中数学知识的一道题目,不过所用到的方法大部分还是初中的内容。有兴趣的
同学可以想一想。
1、一根铝合金型材长为6m,用它制作一个“日”字型的窗框,如果恰好用完这根铝合金型材,那么窗架的长宽各为多少米时,窗架的面积最大?
课堂练习
答案:长为1.5米,宽为1米时,窗框的面积最大.
2、小亮父亲想用长80m的栅栏,再借助房屋的外墙围成一个矩形羊圈ABCD,已知外墙长为50m,设矩形 ABCD的边 AB=xm,面积为Sm
(1)写出S与x之间的关系式、并指出x的取值范围;
(2)当 AB,BC分别为多少求时,羊圈的面积最大 最大面积是多少
课堂练习
答案:(1)S= -2x2+80x(15≤x≤40);
(2)AB=20m,BC=40m时,羊圈面积最大,最大为800m2
【例】如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m时,水面CD的宽是10m.
(1)按如图所示的直角坐标系,求此抛物线的函数表达式;
合作共学
解:设抛物线解析式为y=ax2,
因为抛物线关于y轴对称,AB=20,所以点B的横坐标为10,设点B(10,n),点D(5,n+3),
由题意:
(2)有-条船以5km/h的速度向此桥径直驶来,当船距离此桥35km时.桥下水位正好在AB处.之后水位每小时上涨0.25m.当水位达到CD处时.将禁止船只通行,如果该船的速度不变,那么它能否安全通过此桥
解:由题意得:船行驶到桥下的时间为:35÷5=7小时,
水位上升的高度为:0.25×7=1.75米.
∵1.75<3
∴船的速度不变,它能安全通过此桥.
合作共学
如图,隧道的截面由抛物线和长方形构成,长方形的长为8m,宽是2m。可抛物线可以用y=-x2+4表示.
(1)一辆货运卡车高4m,宽2m,它能通过该隧道吗
(2)如果该隧道内设双向行车道,那么这辆货运卡车是可以通过
跟踪练习
(1)解:
当x=1时,y=3.75,
∵3.75+2=5.75>4,
∴能通过
(2)
当x=2时,y=3,
∵3+2=5.7>4,
∴该隧道设双向车道,这辆车也能通过.
(2010内蒙呼和浩特)如图①是抛物线形拱桥,当水面在n时,拱顶离水面2米,水面宽4米.若水面下降1米,则水面宽度将增加多少米?
跟踪练习
A
B
O
C
D
X
Y
解:按如左图所示的直角坐标系,设抛物线为y=ax2
由题意得:C(-2,-2)、D(2,-2),A,B两点
的纵坐标均为-3.
将C(-2,-2)代入y=ax2得,a=-0.5
∴y=-0.5x2
∴将y=-3代入y=-0.5x2得 x=±√6
∴AB=2√6
∴增加了AB-CD=(2√6-4)米
一、通过利用现实情景或者纯数学情景,培养学生的数学建模能力和应用意识。
它的基本思路是:
课堂小结
二、运用二次函数求最大值的基本模式:
