安徽省安庆市外国语学校2021-2022学年九年级上学期期中数学试卷(word版含答案)
文档属性
| 名称 | 安徽省安庆市外国语学校2021-2022学年九年级上学期期中数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 612.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 08:09:47 | ||
图片预览




文档简介
安庆市外国语学校2021-2022学年九年级上学期期中数学试卷
一、选择题
1. 若,则下列变形错误的是( )
A. B. C. D.
2. 将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
A. y=(x+2)2+4 B. y=(x+2)2﹣4
C. y=(x﹣2)2+4 D. y=(x﹣2)2﹣4
3. 下面四组图形中,必是相似三角形为( )
A. 两个直角三角形
B. 两条边对应成比例,一个对应角相等的两个三角形
C. 有一个角为40°的两个等腰三角形
D. 有一个角为100°的两个等腰三角形
4. 如图,以为顶点的三角形与以为顶点的三角形相似,则这两个三角形的相似比为( )
A. 2:1 B. 3:1 C. 4:3 D. 3:2
5. 点 P 是长度为 1 的线段上的黄金分割点,则较短线段的长度为( )
A. B. 3 - C. D. -2
6. 下列函数中,当x>0时,y随x的增大而减小的是( )
A. y= B. y= C. y=3x+2 D. y=x2﹣3
7. 已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是 ( )
A. a>1 B. -1<a≤1 C. a>0 D. -1<a<2
8. 若P是RtABC直角边BC(∠C=90 ,∠B≠∠A)上异于B、C的一点,过点P作直线截ABC,截得的三角形与原ABC相似,满足这样条件的直线有( )条
A 1 B. 2 C. 3 D. 4
9. 如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
A. 乙>丙>甲 B. 丙>乙>甲 C. 甲>丙>乙 D. 无法判断
10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:①AEF∽CAB;②CF=2AF;③DF=DC;④S四边形CDEF=;其中正确的结论有( )个.
A. ①② B. ①②③ C. ①②④ D. ①②③④
二、填空题
11. 已知三条线段a、b、c,其中a=1cm,b=4cm,c是a、b的比例中项,则c=_____cm.
12. 抛物线y=-x2-2x+m2-1,若其顶点在x轴上,则m=__________.
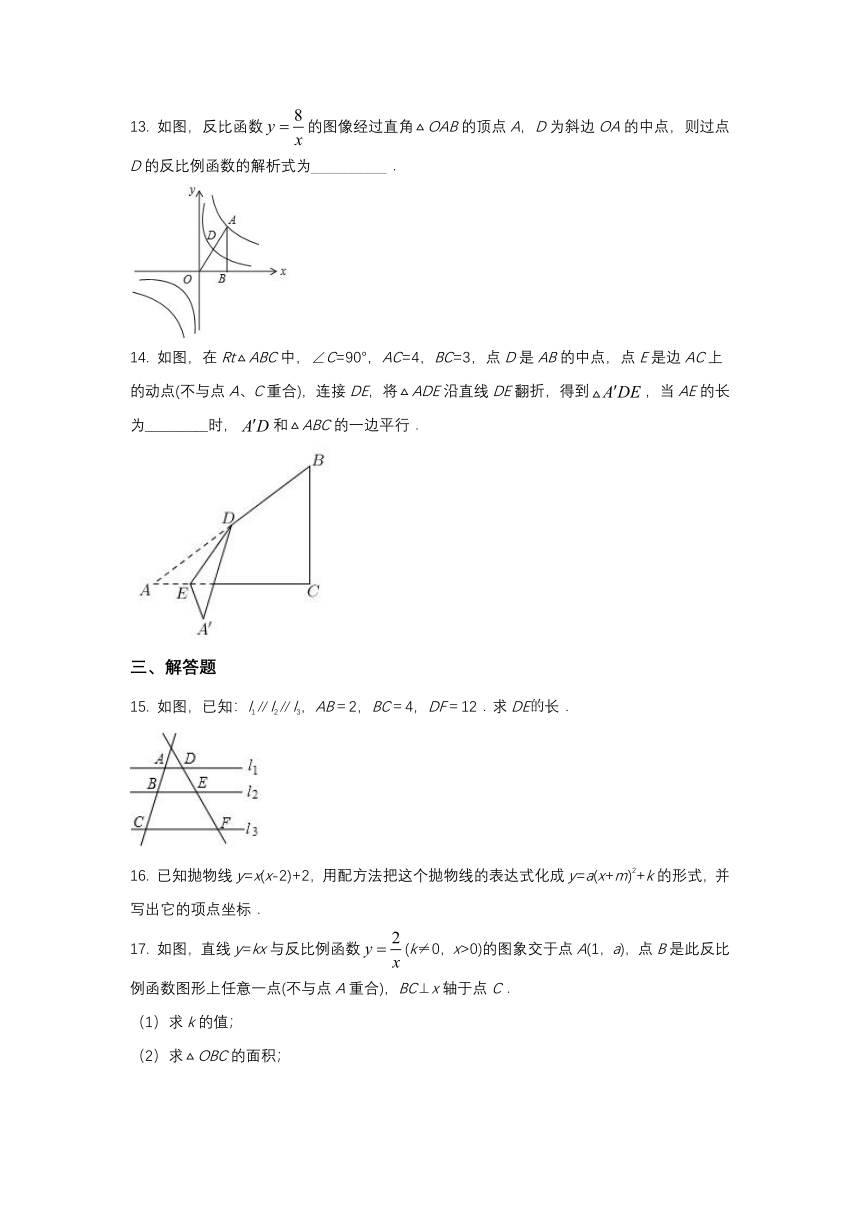
13. 如图,反比函数的图像经过直角OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为__________.
14. 如图,在RtABC中,∠C=90°,AC=4,BC=3,点D是AB的中点,点E是边AC上的动点(不与点A、C重合),连接DE,将ADE沿直线DE翻折,得到,当AE的长为__________时,和ABC的一边平行.
三、解答题
15. 如图,已知:l1∥l2∥l3,AB=2,BC=4,DF=12.求DE长.
16. 已知抛物线y=x(x-2)+2,用配方法把这个抛物线的表达式化成y=a(x+m)2+k的形式,并写出它的项点坐标.
17. 如图,直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求OBC的面积;
18. 如图,正方形网格中每个小正方形的边长为1,ABC 和EDF的点都在网格的格点上.求证:ABC~EDF.
19. 一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.
20. 如图,相邻两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4 m处,另一根电线杆钢索系在离地面6 m处,求中间两根钢索相交处点P离地面的距离.
21. 在ABC中,点D从A出发,在AB边上以每秒一个单位速度向B运动,同时点F从B出发,过点D作DEBC交AC于点E,在BC边上以相同的速度向C运动,运动时间为t秒.
(1) 若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;
(2)连接AF、CD,若BD=DE,求证:∠BAF=∠BCD.
22. 已知二次函数y=x2-2ax+4a+2.
(1)若该函数图象与x轴的一个交点为(-1,0),求a的值;
(2)不论a取何实数,该函数图象总经过一个定点.
①求出这个定点坐标;
②证明这个定点就是所有抛物线顶点纵坐标最大点.
23. 如图,锐角ADC,AO垂直平分BC交CD于O点,B是AD上一点,若记AOC面积为S1,BOD的面积S2,AOD的面积为S3;
(1)求证:;
(2)若= .
①求证: BD=AC·AD;
②若OA=1,求 的值.
安庆市外国语学校2021-2022学年九年级上学期期中数学试卷
一、选择题
1. 若,则下列变形错误的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据比例的性质分析即可,根据已知条件可得,再逐项分析即可
【详解】解:,
A. 由可得,,故该选项正确,不符合题意;
B. 由可得,,故该选项正确,不符合题意;
C. ,故该选项正确,不符合题意;
D. ,故该选项不正确,符合题意
故选D
【点睛】本题考查了比例的性质,掌握比例的性质是解题的关键.
2. 将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
A. y=(x+2)2+4 B. y=(x+2)2﹣4
C. y=(x﹣2)2+4 D. y=(x﹣2)2﹣4
【答案】C
【解析】
【详解】试题分析:抛物线y=x2先向右平移2个单位长度,得:y=(x﹣2)2;再向上平移4个单位长度,得:y=(x﹣2)2+4.故选C.
考点:二次函数表达式的确定.
3. 下面四组图形中,必是相似三角形的为( )
A. 两个直角三角形
B. 两条边对应成比例,一个对应角相等的两个三角形
C. 有一个角为40°的两个等腰三角形
D. 有一个角为100°的两个等腰三角形
【答案】D
【解析】
【分析】根据等腰三角形的性质、直角三角形的性质和相似三角形的判定方法即可判定.
【详解】解:两个直角三角形不一定相似,因为只有一个直角相等,∴A不一定相似;
两条边对应成比例,一个对应角相等的两个三角形不一定相似,因为这个对应角不一定是夹角;∴B不一定相似;
有一个角为40°的两个等腰三角形不一定相似,因为40°的角可能是顶角,也可能是底角,∴C不一定相似;
有一个角为100°的两个等腰三角形一定相似,因为100°的角只能是顶角,所以两个等腰三角形的顶角和底角分别相等,∴D一定相似;
故选D.
【点睛】本题考查了等腰三角形和直角三角形的性质以及相似三角形的判定,属于基础题型,熟练掌握相似三角形的判定方法是关键.
4. 如图,以为顶点的三角形与以为顶点的三角形相似,则这两个三角形的相似比为( )
A. 2:1 B. 3:1 C. 4:3 D. 3:2
【答案】A
【解析】
【分析】通过观察图形可知∠C和∠F是对应角,所以AB和DE是对应边;BC和EF是对应边,即可得出结论.
【详解】解:观察图形可知∠C和∠F对应角,所以AB和DE是对应边;BC和EF是对应边,∵BC=12,EF=6,∴.
故选A.
【点睛】此题重点考察学生对相似三角形性质的理解,掌握相似三角形性质是解题的关键.
5. 点 P 是长度为 1 线段上的黄金分割点,则较短线段的长度为( )
A. B. 3 - C. D. -2
【答案】C
【解析】
【分析】根据黄金分割的定义即把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比,分别进行计算即可.
【详解】点P是长度为 1 的线段上的黄金分割点,
∴较长的线段的长度为,则较短的线段的长度为:1-=;
故选C.
【点睛】此题考查了黄金分割,熟记黄金分割的公式:较短的线段=原线段的,较长的线段=原线段的是本题的关键.
6. 下列函数中,当x>0时,y随x的增大而减小的是( )
A. y= B. y= C. y=3x+2 D. y=x2﹣3
【答案】A
【解析】
【分析】根据一次函数,二次函数,反比例函数及正比例函数的性质判定即可.
【详解】解:A、y=,x>0时y随x的增大而减小,故本选项正确,
B、y=,y随x的增大而增大,故本选项错误,
C、y=3x+2,y随x的增大而增大,故本选项错误,
D、y=x2﹣3,当x>0时,y随x的增大而增大,故本选项错误.
故选A.
【点睛】本题考查了初中阶段常见的三种函数:一次函数,二次函数和反比例函数的性质,属于基本题型,熟练掌握三类常见函数的性质是关键.
7. 已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是 ( )
A. a>1 B. -1<a≤1 C. a>0 D. -1<a<2
【答案】B
【解析】
【详解】试题解析:由题可知,二次函数开口向下,对称轴为 ,所以在对称轴的左侧, 随 的增大而增大,那么 ,又 ,所以取值范围是 .
故本题应选B.
8. 若P是RtABC直角边BC(∠C=90 ,∠B≠∠A)上异于B、C的一点,过点P作直线截ABC,截得的三角形与原ABC相似,满足这样条件的直线有( )条
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
【分析】过点P作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.
【详解】解:由于△ABC是直角三角形,
过P点作直线截△ABC,则截得的三角形与△ABC有一公共角,
所以只要再作一个直角即可使截得的三角形与Rt△ABC相似,
过点P可作AB的垂线、AC的垂线、BC的垂线,共3条直线.
故选:C.
【点睛】本题考查了三角形相似判定定理及其运用.解题时运用了两角法(有两组角对应相等的两个三角形相似)来判定两个三角形相似.
9. 如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
A. 乙>丙>甲 B. 丙>乙>甲 C. 甲>丙>乙 D. 无法判断
【答案】B
【解析】
【分析】过点作于点,根据题意分别表示出甲、乙、丙的面积,然后进行比较即可求解.
【详解】如解图,过点作于点,
则,
,
,
,
则,
,
∴四边形是矩形,
∴甲<乙<丙.
故选:B.
【点睛】此题考查了相似三角形的性质和判定,三角形面积,解题的关键是熟练掌握相似三角形的性质和判定方法.
10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:①AEF∽CAB;②CF=2AF;③DF=DC;④S四边形CDEF=;其中正确的结论有( )个.
A. ①② B. ①②③ C. ①②④ D. ①②③④
【答案】B
【解析】
【分析】①四边形ABCD是矩形,BE⊥AC,则∠ABC=∠AFB=90°,又∠BFA=∠ABC,于是△AEF∽△CAB,故①正确;
②由AE=AD=BC,又AD∥BC,所以=,故②正确;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;
④根据△AEF∽△CBF得到=,求出S△AEF=S△ABF,S△ABF=S矩形ABCD,S四边形CDEF=S△ACD-S△AEF=S矩形ABCD-S矩形ABCD=S矩形ABCD,即可得到S四边形CDEF=5S△AEF,故④错误.
【详解】解:过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴,
∵AE=AD=BC,
∴=,
∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,故③正确;
∵△AEF∽△CBF,
∴=,
∴S△AEF=S△ABF,S△ABF=S矩形ABCD
∴S△AEF=S矩形ABCD,
又∵S四边形CDEF=S△ACD-S△AEF=S矩形ABCD-S矩形ABCD=S矩形ABCD,
∴S四边形CDEF=5S△AEF故④错误;
故选:B.
【点睛】本题考查了相似三角形的判定和性质,矩形的性质,图形面积的计算,正确的作出辅助线是解题的关键.
二、填空题
11. 已知三条线段a、b、c,其中a=1cm,b=4cm,c是a、b的比例中项,则c=_____cm.
【答案】2
【解析】
【分析】根据比例中项的定义,列出比例式即可得出线段c的长,注意线段不能为负.
【详解】解:∵c是a、b的比例中项,∴,即,所以c2=4×1,
解得:c=±2(线段是正数,负值舍去),则c=2cm.
故答案为2.
【点睛】本题考查了比例中项的定义和比例的性质,属于基本题型,熟知概念是关键.
12. 抛物线y=-x2-2x+m2-1,若其顶点在x轴上,则m=__________.
【答案】
【解析】
【分析】直接利用二次函数的性质得出,求出.
【详解】解:∵抛物线y=-x2-2x+m2-的顶点在x轴上,
∴,
解得:,
故答案为:.
【点睛】本题考查了二次函数的性质,正确得出的代数式是解题的关键.
13. 如图,反比函数的图像经过直角OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为__________.
【答案】
【解析】
【分析】过D作DM⊥x轴于M,根据三角形的中位线求出OM=OB,DM=AB,设A的坐标为(a,b),则D(a,b),根据A在反比例函数y=的图象上求出ab=8,即可求出答案.
【详解】解:过D作DM⊥x轴于M,
∵直角三角形OAB,
∴∠ABO=∠DMO=90°,
∴AB∥DM,
∵D为OA的中点,
∴M为OB的中点,
∴OM=OB,DM=AB,
设A的坐标为(a,b),
则OM=a,DM=b,D(a,b),
∵A在反比例函数y=的图象上,
则ab=8,
∴a b=2,
即过点D的反比例函数的解析式为y=,
故答案为:.
【点睛】本题考查了用待定系数法求出反比例函数的图象,直角三角形斜边上中线,三角形的中位线等知识点,能求出ab的值是解此题的关键.
14. 如图,在RtABC中,∠C=90°,AC=4,BC=3,点D是AB的中点,点E是边AC上的动点(不与点A、C重合),连接DE,将ADE沿直线DE翻折,得到,当AE的长为__________时,和ABC的一边平行.
【答案】或
【解析】
【分析】根据和两种情况,利用相似三角形或等腰三角形的性质,求解即可.
【详解】解:由勾股定理得:
当时,设交于点,则
∴
∵点D是AB的中点,可知为的中点,即
设,则,
∵,
∴
∴,即,解得,即
当时,,
又∵
∴
∴
综上可知,或
故答案为或
【点睛】此题考查了折叠的性质,勾股定理,相似三角形的判定与性质,等腰三角形的性质,解题的关键是熟练掌握相关基本性质,并利用分类讨论的思想解决问题.
三、解答题
15. 如图,已知:l1∥l2∥l3,AB=2,BC=4,DF=12.求DE的长.
【答案】4
【解析】
【分析】根据平行线分线段成比例定理列出比例式求解即可.
【详解】解:∵l1∥l2∥l3,AB=2,BC=4,DF=12,
∴,即,解得DE=4.
【点睛】本题考查了平行线分线段成比例定理,属于基础题型,掌握定理是关键.
16. 已知抛物线y=x(x-2)+2,用配方法把这个抛物线的表达式化成y=a(x+m)2+k的形式,并写出它的项点坐标.
【答案】,
【解析】
【分析】直接利用配方法求出二次函数的顶点坐标即可;
【详解】解:y=x(x-2)+2
=x2-2x+2
=(x-1)2+1,
它的顶点坐标为:(1,1);
【点睛】本题考查了二次函数图象与几何变换,正确得出抛物线的顶点式是解题的关键.
17. 如图,直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求OBC的面积;
【答案】(1)2;(2)1
【解析】
【分析】(1)将点A(1,a),代入反比例函数即可求出a=2,然后将A的坐标代入直线y=kx即可求出k的值.
(2)根据反比例函数k的几何意义求解即可.
【详解】解:(1)∵直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),
∴将A(1,a)代入得:a=2,
∴A(1,2),
将A(1,2)代入y=kx,得k=2;
(2)设点B的坐标为(x,y),
∴OC=x,BC=y,
∵点B在反比例函数上,
∴xy=2,
∴.
【点睛】此题考查了一次函数和反比例函数结合问题,反比例函数k的几何意义,解题的关键是根据题意求出a的值.
18. 如图,正方形网格中每个小正方形边长为1,ABC 和EDF的点都在网格的格点上.求证:ABC~EDF.
【答案】见解析
【解析】
【分析】利用勾股定理可分别求出两个三角形的各个边长,再验证对应边的比值相等即可证明.
【详解】解:∵,,,,,,
∴,
∴.
【点睛】本题考查了相似三角形的判定以及勾股定理的运用,验证两个三角形的对应边的比值相等是解题的关键.
19. 一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.
【答案】(1)y=-x2(2)
【解析】
【分析】(1)根据这个函数过原点,那么可设为y=kx2,有CO和AB的长,那么点A的坐标应该是(﹣0.8,﹣2.4),利用待定系数法即可解决;
(2)根据题意令y=﹣(2.4﹣1.5),求出x的值即可得.
【详解】解:(1)设为y=kx2,由CO和AB的长,
那么A的坐标应该是(﹣0.8,﹣2.4),
将其代入函数中得:﹣2.4=0.8×0.8×k,解得k=﹣.
那么函数的解析式就是:y=﹣x2;
(2)根据题意,当y=﹣0.9时,﹣x2=﹣0.9,
解得:x=±,
∴ED=.
【点睛】本题考查了用待定系数法求二次函数的解析式,根据图中信息得出函数经过的点的坐标是解题的关键.
20. 如图,相邻两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4 m处,另一根电线杆钢索系在离地面6 m处,求中间两根钢索相交处点P离地面的距离.
【答案】2.4 m
【解析】
【分析】可过点P作PQ⊥BD于Q,由平行线分线段成比例可得及,进而即可得出PQ的长.
【详解】解:作PQ⊥BD于Q,设BQ=x米,QD=y米,PQ=h米,
∵AB∥PQ∥CD,
∴,,
即及,
∴两式相加得,
由此得h=2.4米.
即点P离地面的高度为2.4米.
【点睛】本题主要考查了平行线分线段成比例的性质问题,应能够熟练运用.
21. 在ABC中,点D从A出发,在AB边上以每秒一个单位的速度向B运动,同时点F从B出发,过点D作DEBC交AC于点E,在BC边上以相同的速度向C运动,运动时间为t秒.
(1) 若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;
(2)连接AF、CD,若BD=DE,求证:∠BAF=∠BCD.
【答案】(1);(2)见解析
【解析】
【分析】(1)根据四边形DFCE是平行四边形,则有,当,根据相似三角形的性质得到关于t的方程,解方程求解即可;
(2)由,可以证得,继而证明,即可得到∠BAF=∠BCD.
【详解】(1)∵,当时,四边形是平行四边形.
∴
∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】此题考查了相似三角形的性质和判定,解题的关键是熟练掌握相似三角形的性质和判定方法.
22 已知二次函数y=x2-2ax+4a+2.
(1)若该函数图象与x轴的一个交点为(-1,0),求a的值;
(2)不论a取何实数,该函数图象总经过一个定点.
①求出这个定点坐标;
②证明这个定点就是所有抛物线顶点纵坐标最大的点.
【答案】(1);(2)①;②见解析
【解析】
分析】(1)把点(-1,0)代入解析式求出a即可;
(2)①整理解析式,令,代入解析式即可得解;②把一般式化为顶点式,根据最大值判断即可;
【详解】(1)把代入得,
∴,
∴.
(2)①整理得,令,代入解析式得,故定点为,
②∵,
∴顶点为,
又∵,
∴当时,纵坐标有最大值6,
∴,,顶点,故定点是所有顶点中纵坐标最大的点.
【点睛】本题主要考查了二次函数与坐标轴的交点和二次函数的顶点式,准确分析计算是解题的关键.
23. 如图,锐角ADC,AO垂直平分BC交CD于O点,B是AD上一点,若记AOC面积为S1,BOD的面积S2,AOD的面积为S3;
(1)求证:;
(2)若= .
①求证: BD=AC·AD;
②若OA=1,求 的值.
【答案】(1)见解析;(2)①见解析;②
【解析】
【分析】(1)通过证明,即可求解;
(2)①过O作交于点E,作交于点F,根据三角形面积公式化简即可;②过点作,根据相似三角形的性质求解即可.
【详解】解:(1)∵垂直平分,
∴
又∵
∴
∴
(2)①过O作交于点E,作交于点F,如下图:
由(1)知
∴,即平分
∴(角平分线的性质)
∵,
又∵,即
∴
∴
∴
②过点作,如下图:
由①可得:
由(1)得:
由题意可得:
∴,即
解得,负值舍去,
又∵
∴
∴
∴
由题意可得:
∵
∴,
∴,
解得:,
【点睛】此题考查了全等三角形的判定与性质,相似三角形的判定与性质,一元二次方程的求解,解题的关键是熟练掌握相关基本性质.
一、选择题
1. 若,则下列变形错误的是( )
A. B. C. D.
2. 将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
A. y=(x+2)2+4 B. y=(x+2)2﹣4
C. y=(x﹣2)2+4 D. y=(x﹣2)2﹣4
3. 下面四组图形中,必是相似三角形为( )
A. 两个直角三角形
B. 两条边对应成比例,一个对应角相等的两个三角形
C. 有一个角为40°的两个等腰三角形
D. 有一个角为100°的两个等腰三角形
4. 如图,以为顶点的三角形与以为顶点的三角形相似,则这两个三角形的相似比为( )
A. 2:1 B. 3:1 C. 4:3 D. 3:2
5. 点 P 是长度为 1 的线段上的黄金分割点,则较短线段的长度为( )
A. B. 3 - C. D. -2
6. 下列函数中,当x>0时,y随x的增大而减小的是( )
A. y= B. y= C. y=3x+2 D. y=x2﹣3
7. 已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是 ( )
A. a>1 B. -1<a≤1 C. a>0 D. -1<a<2
8. 若P是RtABC直角边BC(∠C=90 ,∠B≠∠A)上异于B、C的一点,过点P作直线截ABC,截得的三角形与原ABC相似,满足这样条件的直线有( )条
A 1 B. 2 C. 3 D. 4
9. 如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
A. 乙>丙>甲 B. 丙>乙>甲 C. 甲>丙>乙 D. 无法判断
10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:①AEF∽CAB;②CF=2AF;③DF=DC;④S四边形CDEF=;其中正确的结论有( )个.
A. ①② B. ①②③ C. ①②④ D. ①②③④
二、填空题
11. 已知三条线段a、b、c,其中a=1cm,b=4cm,c是a、b的比例中项,则c=_____cm.
12. 抛物线y=-x2-2x+m2-1,若其顶点在x轴上,则m=__________.
13. 如图,反比函数的图像经过直角OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为__________.
14. 如图,在RtABC中,∠C=90°,AC=4,BC=3,点D是AB的中点,点E是边AC上的动点(不与点A、C重合),连接DE,将ADE沿直线DE翻折,得到,当AE的长为__________时,和ABC的一边平行.
三、解答题
15. 如图,已知:l1∥l2∥l3,AB=2,BC=4,DF=12.求DE长.
16. 已知抛物线y=x(x-2)+2,用配方法把这个抛物线的表达式化成y=a(x+m)2+k的形式,并写出它的项点坐标.
17. 如图,直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求OBC的面积;
18. 如图,正方形网格中每个小正方形的边长为1,ABC 和EDF的点都在网格的格点上.求证:ABC~EDF.
19. 一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.
20. 如图,相邻两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4 m处,另一根电线杆钢索系在离地面6 m处,求中间两根钢索相交处点P离地面的距离.
21. 在ABC中,点D从A出发,在AB边上以每秒一个单位速度向B运动,同时点F从B出发,过点D作DEBC交AC于点E,在BC边上以相同的速度向C运动,运动时间为t秒.
(1) 若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;
(2)连接AF、CD,若BD=DE,求证:∠BAF=∠BCD.
22. 已知二次函数y=x2-2ax+4a+2.
(1)若该函数图象与x轴的一个交点为(-1,0),求a的值;
(2)不论a取何实数,该函数图象总经过一个定点.
①求出这个定点坐标;
②证明这个定点就是所有抛物线顶点纵坐标最大点.
23. 如图,锐角ADC,AO垂直平分BC交CD于O点,B是AD上一点,若记AOC面积为S1,BOD的面积S2,AOD的面积为S3;
(1)求证:;
(2)若= .
①求证: BD=AC·AD;
②若OA=1,求 的值.
安庆市外国语学校2021-2022学年九年级上学期期中数学试卷
一、选择题
1. 若,则下列变形错误的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据比例的性质分析即可,根据已知条件可得,再逐项分析即可
【详解】解:,
A. 由可得,,故该选项正确,不符合题意;
B. 由可得,,故该选项正确,不符合题意;
C. ,故该选项正确,不符合题意;
D. ,故该选项不正确,符合题意
故选D
【点睛】本题考查了比例的性质,掌握比例的性质是解题的关键.
2. 将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
A. y=(x+2)2+4 B. y=(x+2)2﹣4
C. y=(x﹣2)2+4 D. y=(x﹣2)2﹣4
【答案】C
【解析】
【详解】试题分析:抛物线y=x2先向右平移2个单位长度,得:y=(x﹣2)2;再向上平移4个单位长度,得:y=(x﹣2)2+4.故选C.
考点:二次函数表达式的确定.
3. 下面四组图形中,必是相似三角形的为( )
A. 两个直角三角形
B. 两条边对应成比例,一个对应角相等的两个三角形
C. 有一个角为40°的两个等腰三角形
D. 有一个角为100°的两个等腰三角形
【答案】D
【解析】
【分析】根据等腰三角形的性质、直角三角形的性质和相似三角形的判定方法即可判定.
【详解】解:两个直角三角形不一定相似,因为只有一个直角相等,∴A不一定相似;
两条边对应成比例,一个对应角相等的两个三角形不一定相似,因为这个对应角不一定是夹角;∴B不一定相似;
有一个角为40°的两个等腰三角形不一定相似,因为40°的角可能是顶角,也可能是底角,∴C不一定相似;
有一个角为100°的两个等腰三角形一定相似,因为100°的角只能是顶角,所以两个等腰三角形的顶角和底角分别相等,∴D一定相似;
故选D.
【点睛】本题考查了等腰三角形和直角三角形的性质以及相似三角形的判定,属于基础题型,熟练掌握相似三角形的判定方法是关键.
4. 如图,以为顶点的三角形与以为顶点的三角形相似,则这两个三角形的相似比为( )
A. 2:1 B. 3:1 C. 4:3 D. 3:2
【答案】A
【解析】
【分析】通过观察图形可知∠C和∠F是对应角,所以AB和DE是对应边;BC和EF是对应边,即可得出结论.
【详解】解:观察图形可知∠C和∠F对应角,所以AB和DE是对应边;BC和EF是对应边,∵BC=12,EF=6,∴.
故选A.
【点睛】此题重点考察学生对相似三角形性质的理解,掌握相似三角形性质是解题的关键.
5. 点 P 是长度为 1 线段上的黄金分割点,则较短线段的长度为( )
A. B. 3 - C. D. -2
【答案】C
【解析】
【分析】根据黄金分割的定义即把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比,分别进行计算即可.
【详解】点P是长度为 1 的线段上的黄金分割点,
∴较长的线段的长度为,则较短的线段的长度为:1-=;
故选C.
【点睛】此题考查了黄金分割,熟记黄金分割的公式:较短的线段=原线段的,较长的线段=原线段的是本题的关键.
6. 下列函数中,当x>0时,y随x的增大而减小的是( )
A. y= B. y= C. y=3x+2 D. y=x2﹣3
【答案】A
【解析】
【分析】根据一次函数,二次函数,反比例函数及正比例函数的性质判定即可.
【详解】解:A、y=,x>0时y随x的增大而减小,故本选项正确,
B、y=,y随x的增大而增大,故本选项错误,
C、y=3x+2,y随x的增大而增大,故本选项错误,
D、y=x2﹣3,当x>0时,y随x的增大而增大,故本选项错误.
故选A.
【点睛】本题考查了初中阶段常见的三种函数:一次函数,二次函数和反比例函数的性质,属于基本题型,熟练掌握三类常见函数的性质是关键.
7. 已知二次函数y=-x2+2x,当-1<x<a时,y随x的增大而增大,则实数a的取值范围是 ( )
A. a>1 B. -1<a≤1 C. a>0 D. -1<a<2
【答案】B
【解析】
【详解】试题解析:由题可知,二次函数开口向下,对称轴为 ,所以在对称轴的左侧, 随 的增大而增大,那么 ,又 ,所以取值范围是 .
故本题应选B.
8. 若P是RtABC直角边BC(∠C=90 ,∠B≠∠A)上异于B、C的一点,过点P作直线截ABC,截得的三角形与原ABC相似,满足这样条件的直线有( )条
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
【分析】过点P作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.
【详解】解:由于△ABC是直角三角形,
过P点作直线截△ABC,则截得的三角形与△ABC有一公共角,
所以只要再作一个直角即可使截得的三角形与Rt△ABC相似,
过点P可作AB的垂线、AC的垂线、BC的垂线,共3条直线.
故选:C.
【点睛】本题考查了三角形相似判定定理及其运用.解题时运用了两角法(有两组角对应相等的两个三角形相似)来判定两个三角形相似.
9. 如图,将一张三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )
A. 乙>丙>甲 B. 丙>乙>甲 C. 甲>丙>乙 D. 无法判断
【答案】B
【解析】
【分析】过点作于点,根据题意分别表示出甲、乙、丙的面积,然后进行比较即可求解.
【详解】如解图,过点作于点,
则,
,
,
,
则,
,
∴四边形是矩形,
∴甲<乙<丙.
故选:B.
【点睛】此题考查了相似三角形的性质和判定,三角形面积,解题的关键是熟练掌握相似三角形的性质和判定方法.
10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列四个结论:①AEF∽CAB;②CF=2AF;③DF=DC;④S四边形CDEF=;其中正确的结论有( )个.
A. ①② B. ①②③ C. ①②④ D. ①②③④
【答案】B
【解析】
【分析】①四边形ABCD是矩形,BE⊥AC,则∠ABC=∠AFB=90°,又∠BFA=∠ABC,于是△AEF∽△CAB,故①正确;
②由AE=AD=BC,又AD∥BC,所以=,故②正确;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;
④根据△AEF∽△CBF得到=,求出S△AEF=S△ABF,S△ABF=S矩形ABCD,S四边形CDEF=S△ACD-S△AEF=S矩形ABCD-S矩形ABCD=S矩形ABCD,即可得到S四边形CDEF=5S△AEF,故④错误.
【详解】解:过D作DM∥BE交AC于N,
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴,
∵AE=AD=BC,
∴=,
∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,故③正确;
∵△AEF∽△CBF,
∴=,
∴S△AEF=S△ABF,S△ABF=S矩形ABCD
∴S△AEF=S矩形ABCD,
又∵S四边形CDEF=S△ACD-S△AEF=S矩形ABCD-S矩形ABCD=S矩形ABCD,
∴S四边形CDEF=5S△AEF故④错误;
故选:B.
【点睛】本题考查了相似三角形的判定和性质,矩形的性质,图形面积的计算,正确的作出辅助线是解题的关键.
二、填空题
11. 已知三条线段a、b、c,其中a=1cm,b=4cm,c是a、b的比例中项,则c=_____cm.
【答案】2
【解析】
【分析】根据比例中项的定义,列出比例式即可得出线段c的长,注意线段不能为负.
【详解】解:∵c是a、b的比例中项,∴,即,所以c2=4×1,
解得:c=±2(线段是正数,负值舍去),则c=2cm.
故答案为2.
【点睛】本题考查了比例中项的定义和比例的性质,属于基本题型,熟知概念是关键.
12. 抛物线y=-x2-2x+m2-1,若其顶点在x轴上,则m=__________.
【答案】
【解析】
【分析】直接利用二次函数的性质得出,求出.
【详解】解:∵抛物线y=-x2-2x+m2-的顶点在x轴上,
∴,
解得:,
故答案为:.
【点睛】本题考查了二次函数的性质,正确得出的代数式是解题的关键.
13. 如图,反比函数的图像经过直角OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式为__________.
【答案】
【解析】
【分析】过D作DM⊥x轴于M,根据三角形的中位线求出OM=OB,DM=AB,设A的坐标为(a,b),则D(a,b),根据A在反比例函数y=的图象上求出ab=8,即可求出答案.
【详解】解:过D作DM⊥x轴于M,
∵直角三角形OAB,
∴∠ABO=∠DMO=90°,
∴AB∥DM,
∵D为OA的中点,
∴M为OB的中点,
∴OM=OB,DM=AB,
设A的坐标为(a,b),
则OM=a,DM=b,D(a,b),
∵A在反比例函数y=的图象上,
则ab=8,
∴a b=2,
即过点D的反比例函数的解析式为y=,
故答案为:.
【点睛】本题考查了用待定系数法求出反比例函数的图象,直角三角形斜边上中线,三角形的中位线等知识点,能求出ab的值是解此题的关键.
14. 如图,在RtABC中,∠C=90°,AC=4,BC=3,点D是AB的中点,点E是边AC上的动点(不与点A、C重合),连接DE,将ADE沿直线DE翻折,得到,当AE的长为__________时,和ABC的一边平行.
【答案】或
【解析】
【分析】根据和两种情况,利用相似三角形或等腰三角形的性质,求解即可.
【详解】解:由勾股定理得:
当时,设交于点,则
∴
∵点D是AB的中点,可知为的中点,即
设,则,
∵,
∴
∴,即,解得,即
当时,,
又∵
∴
∴
综上可知,或
故答案为或
【点睛】此题考查了折叠的性质,勾股定理,相似三角形的判定与性质,等腰三角形的性质,解题的关键是熟练掌握相关基本性质,并利用分类讨论的思想解决问题.
三、解答题
15. 如图,已知:l1∥l2∥l3,AB=2,BC=4,DF=12.求DE的长.
【答案】4
【解析】
【分析】根据平行线分线段成比例定理列出比例式求解即可.
【详解】解:∵l1∥l2∥l3,AB=2,BC=4,DF=12,
∴,即,解得DE=4.
【点睛】本题考查了平行线分线段成比例定理,属于基础题型,掌握定理是关键.
16. 已知抛物线y=x(x-2)+2,用配方法把这个抛物线的表达式化成y=a(x+m)2+k的形式,并写出它的项点坐标.
【答案】,
【解析】
【分析】直接利用配方法求出二次函数的顶点坐标即可;
【详解】解:y=x(x-2)+2
=x2-2x+2
=(x-1)2+1,
它的顶点坐标为:(1,1);
【点睛】本题考查了二次函数图象与几何变换,正确得出抛物线的顶点式是解题的关键.
17. 如图,直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),点B是此反比例函数图形上任意一点(不与点A重合),BC⊥x轴于点C.
(1)求k的值;
(2)求OBC的面积;
【答案】(1)2;(2)1
【解析】
【分析】(1)将点A(1,a),代入反比例函数即可求出a=2,然后将A的坐标代入直线y=kx即可求出k的值.
(2)根据反比例函数k的几何意义求解即可.
【详解】解:(1)∵直线y=kx与反比例函数(k≠0,x>0)的图象交于点A(1,a),
∴将A(1,a)代入得:a=2,
∴A(1,2),
将A(1,2)代入y=kx,得k=2;
(2)设点B的坐标为(x,y),
∴OC=x,BC=y,
∵点B在反比例函数上,
∴xy=2,
∴.
【点睛】此题考查了一次函数和反比例函数结合问题,反比例函数k的几何意义,解题的关键是根据题意求出a的值.
18. 如图,正方形网格中每个小正方形边长为1,ABC 和EDF的点都在网格的格点上.求证:ABC~EDF.
【答案】见解析
【解析】
【分析】利用勾股定理可分别求出两个三角形的各个边长,再验证对应边的比值相等即可证明.
【详解】解:∵,,,,,,
∴,
∴.
【点睛】本题考查了相似三角形的判定以及勾股定理的运用,验证两个三角形的对应边的比值相等是解题的关键.
19. 一个涵洞成抛物线形,它的截面如图,现测得:当水面宽AB=1.6 m时,涵洞顶点与水面的距离为2.4 m,离开水面1.5 m处是涵洞宽ED.
(1)求抛物线的解析式;
(2)求ED的长.
【答案】(1)y=-x2(2)
【解析】
【分析】(1)根据这个函数过原点,那么可设为y=kx2,有CO和AB的长,那么点A的坐标应该是(﹣0.8,﹣2.4),利用待定系数法即可解决;
(2)根据题意令y=﹣(2.4﹣1.5),求出x的值即可得.
【详解】解:(1)设为y=kx2,由CO和AB的长,
那么A的坐标应该是(﹣0.8,﹣2.4),
将其代入函数中得:﹣2.4=0.8×0.8×k,解得k=﹣.
那么函数的解析式就是:y=﹣x2;
(2)根据题意,当y=﹣0.9时,﹣x2=﹣0.9,
解得:x=±,
∴ED=.
【点睛】本题考查了用待定系数法求二次函数的解析式,根据图中信息得出函数经过的点的坐标是解题的关键.
20. 如图,相邻两根电线杆都用钢索在地面上固定,一根电线杆钢索系在离地面4 m处,另一根电线杆钢索系在离地面6 m处,求中间两根钢索相交处点P离地面的距离.
【答案】2.4 m
【解析】
【分析】可过点P作PQ⊥BD于Q,由平行线分线段成比例可得及,进而即可得出PQ的长.
【详解】解:作PQ⊥BD于Q,设BQ=x米,QD=y米,PQ=h米,
∵AB∥PQ∥CD,
∴,,
即及,
∴两式相加得,
由此得h=2.4米.
即点P离地面的高度为2.4米.
【点睛】本题主要考查了平行线分线段成比例的性质问题,应能够熟练运用.
21. 在ABC中,点D从A出发,在AB边上以每秒一个单位的速度向B运动,同时点F从B出发,过点D作DEBC交AC于点E,在BC边上以相同的速度向C运动,运动时间为t秒.
(1) 若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;
(2)连接AF、CD,若BD=DE,求证:∠BAF=∠BCD.
【答案】(1);(2)见解析
【解析】
【分析】(1)根据四边形DFCE是平行四边形,则有,当,根据相似三角形的性质得到关于t的方程,解方程求解即可;
(2)由,可以证得,继而证明,即可得到∠BAF=∠BCD.
【详解】(1)∵,当时,四边形是平行四边形.
∴
∵,
∴,
∴,
∴.
(2)证明:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
【点睛】此题考查了相似三角形的性质和判定,解题的关键是熟练掌握相似三角形的性质和判定方法.
22 已知二次函数y=x2-2ax+4a+2.
(1)若该函数图象与x轴的一个交点为(-1,0),求a的值;
(2)不论a取何实数,该函数图象总经过一个定点.
①求出这个定点坐标;
②证明这个定点就是所有抛物线顶点纵坐标最大的点.
【答案】(1);(2)①;②见解析
【解析】
分析】(1)把点(-1,0)代入解析式求出a即可;
(2)①整理解析式,令,代入解析式即可得解;②把一般式化为顶点式,根据最大值判断即可;
【详解】(1)把代入得,
∴,
∴.
(2)①整理得,令,代入解析式得,故定点为,
②∵,
∴顶点为,
又∵,
∴当时,纵坐标有最大值6,
∴,,顶点,故定点是所有顶点中纵坐标最大的点.
【点睛】本题主要考查了二次函数与坐标轴的交点和二次函数的顶点式,准确分析计算是解题的关键.
23. 如图,锐角ADC,AO垂直平分BC交CD于O点,B是AD上一点,若记AOC面积为S1,BOD的面积S2,AOD的面积为S3;
(1)求证:;
(2)若= .
①求证: BD=AC·AD;
②若OA=1,求 的值.
【答案】(1)见解析;(2)①见解析;②
【解析】
【分析】(1)通过证明,即可求解;
(2)①过O作交于点E,作交于点F,根据三角形面积公式化简即可;②过点作,根据相似三角形的性质求解即可.
【详解】解:(1)∵垂直平分,
∴
又∵
∴
∴
(2)①过O作交于点E,作交于点F,如下图:
由(1)知
∴,即平分
∴(角平分线的性质)
∵,
又∵,即
∴
∴
∴
②过点作,如下图:
由①可得:
由(1)得:
由题意可得:
∴,即
解得,负值舍去,
又∵
∴
∴
∴
由题意可得:
∵
∴,
∴,
解得:,
【点睛】此题考查了全等三角形的判定与性质,相似三角形的判定与性质,一元二次方程的求解,解题的关键是熟练掌握相关基本性质.
同课章节目录
