内蒙古自治区巴彦淖尔市临河区第三高级中学2021-2022学年高二上学期期中考试数学(理)试卷(Word版含答案)
文档属性
| 名称 | 内蒙古自治区巴彦淖尔市临河区第三高级中学2021-2022学年高二上学期期中考试数学(理)试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 772.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 20:58:03 | ||
图片预览



文档简介
临河三中2021~2022学年第一学期期中考试
高二(理科数学)试卷
试卷总分:150分 考试时间:120分钟
第Ⅰ卷(共60分)
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知直线过、两点,则直线的倾斜角的大小为( )
A. B. C. D.
2.若直线平分圆的周长,则( )
A.9 B.-9 C.1 D.-1
3.已知直线与直线互相平行,且两者之间的距离是,则等于( )
A.0 B.-1 C.1 D.2
4.如图所示的程序框图,若输出的,则输入的值为( )
A. B. C. D.或
5.以,为端点的线段的垂直平分线方程是( )
A. B. C. D.
6.已知圆与圆有3条公切线,则( )
A. B. C.或 D.或
7.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
A.20 B.10 C.30 D.60
8.若三棱锥的三条侧棱两两垂直,且三条侧棱长分别为1,,,则其外接球的表面积是( )
A. B. C. D.
9.已知圆,圆与圆关于直线对称,则圆的方程为( )
A. B.
C. D.
10.一条光线从点射出,经轴反射后与圆相切,则反射光线所在直线的斜率为( )
A.或 B.或 C.或 D.或
11.已知圆的方程为,设该圆过点的最长弦和最短弦分别为和,则四边形的面积为( )
A. B. C. D.
12.过点作直线(不同时为零)的垂线,垂足为,点,则的取值范围是( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本题共4小题,每小题5分,共20分。
13.在空间直角坐标系中,点P(2, -1, 1)在yOz平面内的射影为Q(x, y, z),则x+y+z =________.
14.已知两点,则以线段为直径的圆的标准方程为___________.
15.函数 且)的图象必过点A,则过点A且与直线2x+y-3=0平行的直线方程是____________________.
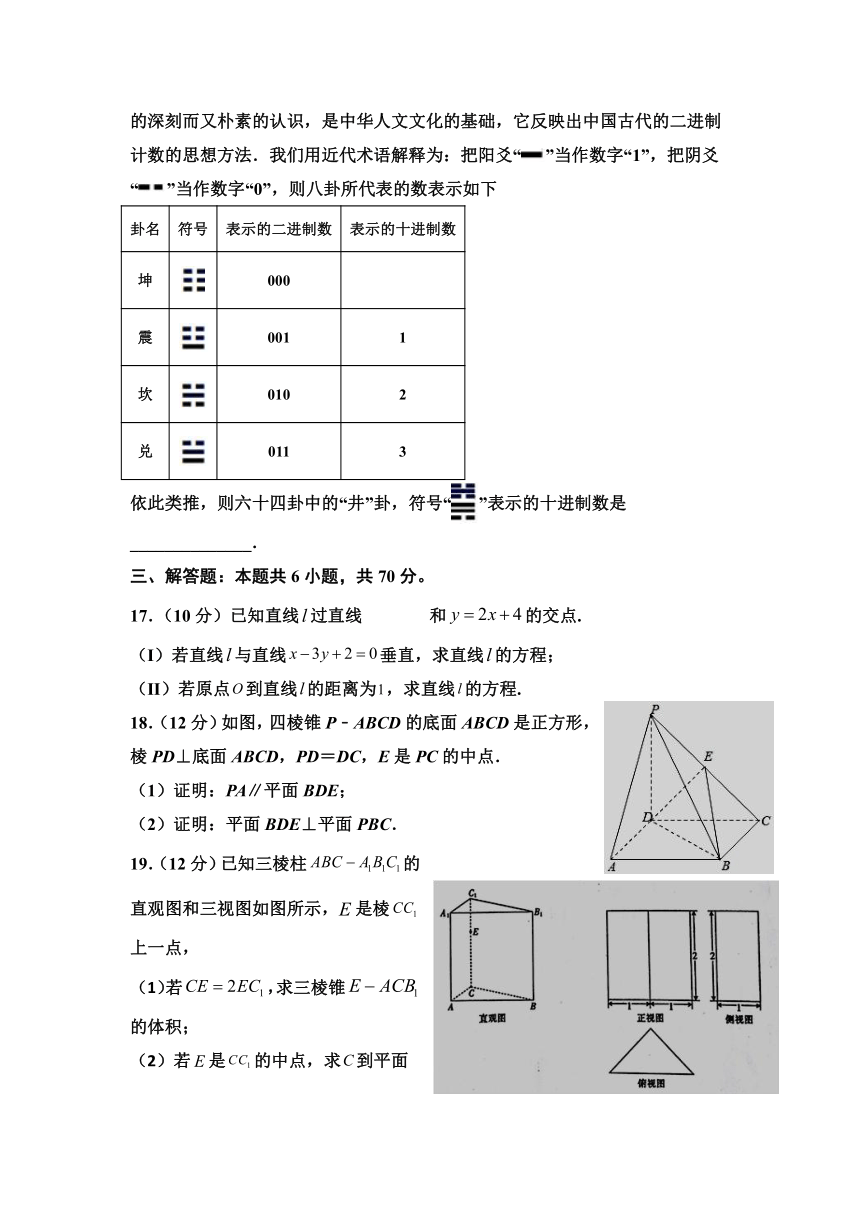
16.《周易》历来被人们视作儒家群经之首,它表现了古代中华民族对万事万物的深刻而又朴素的认识,是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法.我们用近代术语解释为:把阳爻“”当作数字“1”,把阴爻“”当作数字“0”,则八卦所代表的数表示如下
卦名 符号 表示的二进制数 表示的十进制数
坤 000
震 001 1
坎 010 2
兑 011 3
依此类推,则六十四卦中的“井”卦,符号“”表示的十进制数是______________.
三、解答题:本题共6小题,共70分。
17.(10分)已知直线过直线 和的交点.
(Ⅰ)若直线与直线垂直,求直线的方程;
(Ⅱ)若原点到直线的距离为,求直线的方程.
18.(12分)如图,四棱锥P﹣ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明:PA∥平面BDE;
(2)证明:平面BDE⊥平面PBC.
19.(12分)已知三棱柱的直观图和三视图如图所示,是棱上一点,
(1)若,求三棱锥的体积;
(2)若是的中点,求到平面的距离.
20.(12分)已知以点C为圆心的圆经过点和,且圆心在直线上.
(1)求圆C的方程; (2)设点P在圆C上,求△PAB的面积的最大值.
21.(12分)已知以点为圆心的圆与直线:相切,过点的动直线与圆相交于、两点,是的中点.
(1)求圆的方程;
(2)当时,求直线的方程.
22.(12分)在平面直角坐标系xOy中,已知直线l:x+y-1=0和圆C:,P是直线l上的一点,过点P可以作圆C的两条切线.
(1)求点P的横坐标的取值范围;
(2)若点P在第四象限,过点P的两条切线互相垂直,求这两条切线的方程.
参考答案
1.C 2.B 3.A 4.D 5.B 6.C 7.B 8.C 9.B 10.D 11.A 12.D
13.0 14. 15. 16.22
17.解(1)由,得交点,
由于直线与直线垂直,可设直线的方程为,
将交点坐标代入得,得,因此,所求直线的方程为;
(2)如果直线轴,则直线的方程为,且原点到直线的距离为,合乎题意;
如果直线的斜率存在时,可设直线的方程为,即,
原点到直线的距离为,解得,
此时,直线的方程为,即.
综上所述,直线的方程为和.
18.证明:(1)连结AC,设AC与BD交于O点,连结EO.
∵底面ABCD是正方形,
∴O为AC的中点,又E为PC的中点,
∴OE∥PA,
∵OE 平面BDE,PA 平面BDE,
∴PA∥平面BDE;
(2)∵PD=DC,E是PC的中点,
∴DE⊥PC,
∵PD⊥平面ABCD,平面ABCD,∴PD⊥AD,
又由于AD⊥CD,PD∩CD=D,故AD⊥平面PCD,
又平面PCD,所以AD⊥DE,
又由题意得AD∥BC,故BC⊥DE,
于是,由BC∩PC=C,DE⊥PC,BC⊥DE,可得DE⊥平面PBC,
又因平面BDE,所以平面BDE⊥平面PBC.
19.解(1)由三视图得,该三棱柱是侧棱长为2的直三棱柱,底面是以为斜边的等腰直角三角形,且,
∴平面,平面,
∵,,∴,又,
∴.
(2)∵是的中点,∴,
∴,即为等腰三角形,
∵,∴的高为,
设到平面的距离为,
∵,
∴,
解得.
20.解析:(1)依题意所求圆的圆心为的垂直平分线和直线的交点,
中点为斜率为,垂直平分线方程为,即.
联立解得即圆心,半径,
所求圆方程为.
(2),圆心到的距离为,
到距离的最大值为,
所以面积的最大值为
21.解(1)设圆的半径为,由于圆与直线相切,
,
圆的方程为;
(2)①当直线与轴垂直时,易知符合题意;
②当直线与轴不垂直时,
设直线的方程为,即,
连接,则
,,
则由,得,直线.
故直线的方程为或.
22.解(1)联立解得或
∴直线与圆的两个交点坐标分别为和.
∵过点可以作圆的两条切线,
∴点在圆外,
∴点的横坐标的取值范围.
(2)设,,过点可以作圆的两条切线,切点分别为,,
由两条切线互相垂直,
∴四边形为正方形,且边长为,则,
∴,解得或(舍去),则.
设切线方程为,,
则圆心到切线的距离,解得或.
∴切线方程为或,
即或.
高二(理科数学)试卷
试卷总分:150分 考试时间:120分钟
第Ⅰ卷(共60分)
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知直线过、两点,则直线的倾斜角的大小为( )
A. B. C. D.
2.若直线平分圆的周长,则( )
A.9 B.-9 C.1 D.-1
3.已知直线与直线互相平行,且两者之间的距离是,则等于( )
A.0 B.-1 C.1 D.2
4.如图所示的程序框图,若输出的,则输入的值为( )
A. B. C. D.或
5.以,为端点的线段的垂直平分线方程是( )
A. B. C. D.
6.已知圆与圆有3条公切线,则( )
A. B. C.或 D.或
7.某三棱锥的三视图如图所示,则该三棱锥的体积为( )
A.20 B.10 C.30 D.60
8.若三棱锥的三条侧棱两两垂直,且三条侧棱长分别为1,,,则其外接球的表面积是( )
A. B. C. D.
9.已知圆,圆与圆关于直线对称,则圆的方程为( )
A. B.
C. D.
10.一条光线从点射出,经轴反射后与圆相切,则反射光线所在直线的斜率为( )
A.或 B.或 C.或 D.或
11.已知圆的方程为,设该圆过点的最长弦和最短弦分别为和,则四边形的面积为( )
A. B. C. D.
12.过点作直线(不同时为零)的垂线,垂足为,点,则的取值范围是( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本题共4小题,每小题5分,共20分。
13.在空间直角坐标系中,点P(2, -1, 1)在yOz平面内的射影为Q(x, y, z),则x+y+z =________.
14.已知两点,则以线段为直径的圆的标准方程为___________.
15.函数 且)的图象必过点A,则过点A且与直线2x+y-3=0平行的直线方程是____________________.
16.《周易》历来被人们视作儒家群经之首,它表现了古代中华民族对万事万物的深刻而又朴素的认识,是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法.我们用近代术语解释为:把阳爻“”当作数字“1”,把阴爻“”当作数字“0”,则八卦所代表的数表示如下
卦名 符号 表示的二进制数 表示的十进制数
坤 000
震 001 1
坎 010 2
兑 011 3
依此类推,则六十四卦中的“井”卦,符号“”表示的十进制数是______________.
三、解答题:本题共6小题,共70分。
17.(10分)已知直线过直线 和的交点.
(Ⅰ)若直线与直线垂直,求直线的方程;
(Ⅱ)若原点到直线的距离为,求直线的方程.
18.(12分)如图,四棱锥P﹣ABCD的底面ABCD是正方形,棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明:PA∥平面BDE;
(2)证明:平面BDE⊥平面PBC.
19.(12分)已知三棱柱的直观图和三视图如图所示,是棱上一点,
(1)若,求三棱锥的体积;
(2)若是的中点,求到平面的距离.
20.(12分)已知以点C为圆心的圆经过点和,且圆心在直线上.
(1)求圆C的方程; (2)设点P在圆C上,求△PAB的面积的最大值.
21.(12分)已知以点为圆心的圆与直线:相切,过点的动直线与圆相交于、两点,是的中点.
(1)求圆的方程;
(2)当时,求直线的方程.
22.(12分)在平面直角坐标系xOy中,已知直线l:x+y-1=0和圆C:,P是直线l上的一点,过点P可以作圆C的两条切线.
(1)求点P的横坐标的取值范围;
(2)若点P在第四象限,过点P的两条切线互相垂直,求这两条切线的方程.
参考答案
1.C 2.B 3.A 4.D 5.B 6.C 7.B 8.C 9.B 10.D 11.A 12.D
13.0 14. 15. 16.22
17.解(1)由,得交点,
由于直线与直线垂直,可设直线的方程为,
将交点坐标代入得,得,因此,所求直线的方程为;
(2)如果直线轴,则直线的方程为,且原点到直线的距离为,合乎题意;
如果直线的斜率存在时,可设直线的方程为,即,
原点到直线的距离为,解得,
此时,直线的方程为,即.
综上所述,直线的方程为和.
18.证明:(1)连结AC,设AC与BD交于O点,连结EO.
∵底面ABCD是正方形,
∴O为AC的中点,又E为PC的中点,
∴OE∥PA,
∵OE 平面BDE,PA 平面BDE,
∴PA∥平面BDE;
(2)∵PD=DC,E是PC的中点,
∴DE⊥PC,
∵PD⊥平面ABCD,平面ABCD,∴PD⊥AD,
又由于AD⊥CD,PD∩CD=D,故AD⊥平面PCD,
又平面PCD,所以AD⊥DE,
又由题意得AD∥BC,故BC⊥DE,
于是,由BC∩PC=C,DE⊥PC,BC⊥DE,可得DE⊥平面PBC,
又因平面BDE,所以平面BDE⊥平面PBC.
19.解(1)由三视图得,该三棱柱是侧棱长为2的直三棱柱,底面是以为斜边的等腰直角三角形,且,
∴平面,平面,
∵,,∴,又,
∴.
(2)∵是的中点,∴,
∴,即为等腰三角形,
∵,∴的高为,
设到平面的距离为,
∵,
∴,
解得.
20.解析:(1)依题意所求圆的圆心为的垂直平分线和直线的交点,
中点为斜率为,垂直平分线方程为,即.
联立解得即圆心,半径,
所求圆方程为.
(2),圆心到的距离为,
到距离的最大值为,
所以面积的最大值为
21.解(1)设圆的半径为,由于圆与直线相切,
,
圆的方程为;
(2)①当直线与轴垂直时,易知符合题意;
②当直线与轴不垂直时,
设直线的方程为,即,
连接,则
,,
则由,得,直线.
故直线的方程为或.
22.解(1)联立解得或
∴直线与圆的两个交点坐标分别为和.
∵过点可以作圆的两条切线,
∴点在圆外,
∴点的横坐标的取值范围.
(2)设,,过点可以作圆的两条切线,切点分别为,,
由两条切线互相垂直,
∴四边形为正方形,且边长为,则,
∴,解得或(舍去),则.
设切线方程为,,
则圆心到切线的距离,解得或.
∴切线方程为或,
即或.
同课章节目录
