沪科版2021-2022学年八年级数学上册12.3 一次函数与二元一次方程 同步测试卷(word版、含答案)
文档属性
| 名称 | 沪科版2021-2022学年八年级数学上册12.3 一次函数与二元一次方程 同步测试卷(word版、含答案) | 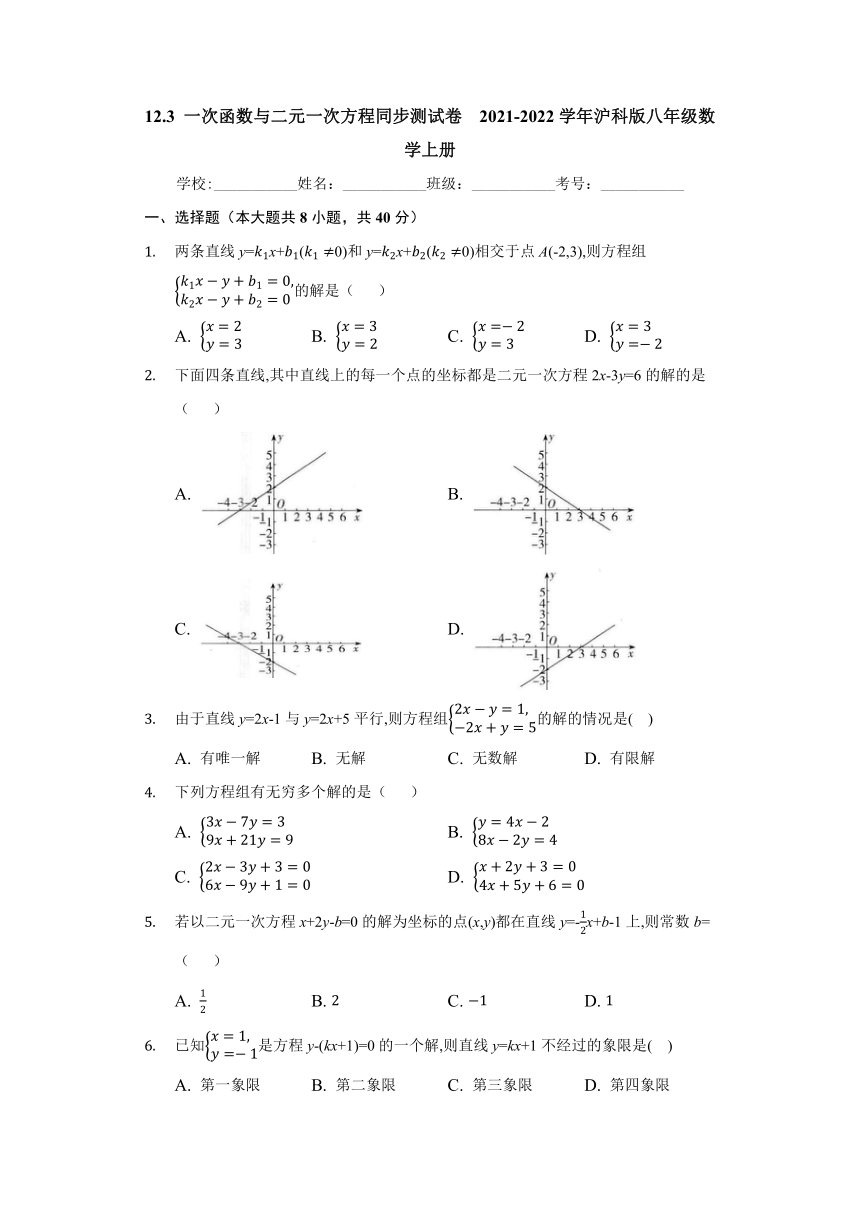 | |
| 格式 | docx | ||
| 文件大小 | 130.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 15:04:14 | ||
图片预览



文档简介
12.3 一次函数与二元一次方程同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
两条直线y=x+(0)和y=x+(0)相交于点A(-2,3),则方程组的解是( )
A. B. C. D.
下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x-3y=6的解的是( )
A. B.
C. D.
由于直线y=2x-1与y=2x+5平行,则方程组的解的情况是( )
A. 有唯一解 B. 无解 C. 无数解 D. 有限解
下列方程组有无穷多个解的是( )
A. B.
C. D.
若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-x+b-1上,则常数b=( )
A. B. C. D.
已知是方程y-(kx+1)=0的一个解,则直线y=kx+1不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
甲、乙两人登山,登山过程中,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示.乙提速后,乙的登山速度是甲登山速度的3倍,并先到达山顶.根据图象所提供的信息,下列说法正确的有( )
甲登山的速度是每分钟10米;
乙在A地时距地面的高度b为30米;
乙登山5.5分钟时追上甲;
登山时间为4分钟,9分钟或15分钟时,甲、乙两人距地面的高度差为50米.
A. 个 B. 个 C. 个 D. 个
已知直线y=kx+2与直线y=x交于点P,且点P的横坐标为2,下列结论正确的是( )
关于x的方程kx+2=0的解为x=3;对于直线y=kx+2,当x<3时,y>0;
不等式组0kx+2x的解集是2x3.
A. B. C. D.
二、填空题(本大题共4小题,共20分)
若方程组无解,则y=kx-2图象不经过第 象限.
元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之.”图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是_ ___.
利用图象法解关于x,y的方程组时,若表示两方程的直线重合,则m= ,n= ;若表示两方程的直线平行,则mn= 且n .
若一次函数y=kx+b(k0)的图象经过点A(2021,2020),
B(2020,2019),则 ____(填“是”或“不是”)二元一次方程kx-y+b=0的解.
三、解答题(本大题共3小题,共40分)
在同一直角坐标系中画出一次函数=-2x+2与=x-4的图象,并根据图象解答下列问题:
(1)直线=-2x+2,=x-4与y轴分别相交于点A,B,请写出A,B两点的坐标;
(2)根据图象写出方程组的解;
(3)若与相交于点P,求APB的面积.
如图,直线m:3x+3y=12与x轴交于点A,与y轴交于点B,直线n:ax+by=-5与x轴交于点C,与直线m交于点P,若点P的横坐标为1.
(1)求A,B两点的坐标;
(2)直接写出方程组的解;
(3)求a和b的值;
(4)求三角形PAC的面积.
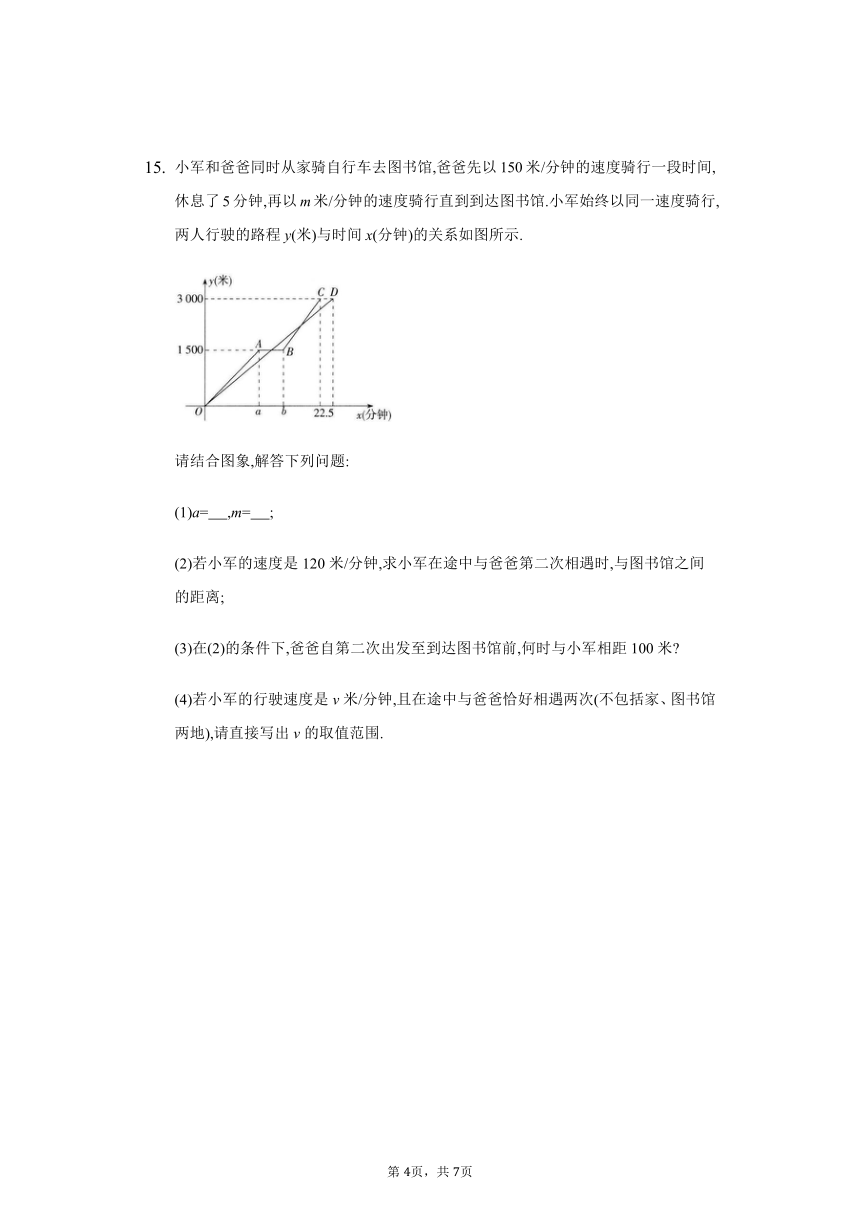
小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分钟的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度骑行直到到达图书馆.小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图所示.
请结合图象,解答下列问题:
(1)a= ,m= ;
(2)若小军的速度是120米/分钟,求小军在途中与爸爸第二次相遇时,与图书馆之间的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米
(4)若小军的行驶速度是v米/分钟,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
参考答案
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】一
10.【答案】(32,4800)
11.【答案】 -3 -4 -3
12.【答案】是
13.【答案】解:画一次函数=-2x+2与=x-4的图象如图.
(1)由图象可知,A,B两点的坐标分别为A(0,2),B(0,-4).
(2)由图象知,直线=-2x+2与=x-4的交点坐标为(2,-2),
所以方程组的解为
(3)=(2+4)2=6.
14.【答案】解:(1)令3x+3y=12中y=0,则3x=12,
解得x=4,
所以点A的坐标为(4,0).
令3x+3y=12中x=0,则3y=12,
解得y=4,
所以点B的坐标为(0,4).
(2)令3x+3y=12中x=1,则3+3y=12,
解得y=3,
所以点P的坐标为(1,3).
所以方程组的解是
(3)将C,P(1,3)代入ax+by=-5中,得解得
(4)AC=4-=,
所以=3=8.5.
15.【答案】解:(1)爸爸先以150米/分钟的速度骑行1500米,a==10.
爸爸休息了5分钟,b=a+5=10+5=15,m==200.
(2)设线段BC的解析式为y=kx+(k0),
B(15,1500),C(22.5,3000),解得
线段BC的解析式为y=200x-1500(15x22.5).
小军的速度是120米/分钟,
走完3000米所用时间为t==25(分钟),点D的坐标为(25,3000),
设线段OD的函数解析式为y=x(0),则=3000,解得=120.
线段OD的函数解析式为y=120x(0x25).
由题图知,第二次相遇点为OD与BC的交点,联立得解得
OD与BC的交点坐标为(,2250).
小军在途中与爸爸第二次相遇时,与图书馆之间的距离为3000-2250=750(米).
(3)爸爸自第二次出发,所行驶的路程y(米)与时间x(分钟)的函数解析式为y=200x-1500(15x22.5).
当<时,-=100,即120x-(200x-1500)=100,解得x=17.5.
15<17.5<22.5,x=17.5符合题意;
当>时,-=100,即200x-1500-120x=100,解得x=20.
15<20<22.5,x=20符合题意.
综上所述,爸爸自第二次出发至到达图书馆前,在17.5分钟和20分钟时与小军相距100米.
(4)如图,当线段OD过点B时,小军的速度为150015=100(米/分钟);
当线段OD过点C时,小军的速度为300022.5=(米/分钟).
结合图象可知,当100<v<时,小军在途中与爸爸恰好相遇两次(不包括家、图书馆两地).
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
两条直线y=x+(0)和y=x+(0)相交于点A(-2,3),则方程组的解是( )
A. B. C. D.
下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x-3y=6的解的是( )
A. B.
C. D.
由于直线y=2x-1与y=2x+5平行,则方程组的解的情况是( )
A. 有唯一解 B. 无解 C. 无数解 D. 有限解
下列方程组有无穷多个解的是( )
A. B.
C. D.
若以二元一次方程x+2y-b=0的解为坐标的点(x,y)都在直线y=-x+b-1上,则常数b=( )
A. B. C. D.
已知是方程y-(kx+1)=0的一个解,则直线y=kx+1不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
甲、乙两人登山,登山过程中,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示.乙提速后,乙的登山速度是甲登山速度的3倍,并先到达山顶.根据图象所提供的信息,下列说法正确的有( )
甲登山的速度是每分钟10米;
乙在A地时距地面的高度b为30米;
乙登山5.5分钟时追上甲;
登山时间为4分钟,9分钟或15分钟时,甲、乙两人距地面的高度差为50米.
A. 个 B. 个 C. 个 D. 个
已知直线y=kx+2与直线y=x交于点P,且点P的横坐标为2,下列结论正确的是( )
关于x的方程kx+2=0的解为x=3;对于直线y=kx+2,当x<3时,y>0;
不等式组0kx+2x的解集是2x3.
A. B. C. D.
二、填空题(本大题共4小题,共20分)
若方程组无解,则y=kx-2图象不经过第 象限.
元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之.”图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点P的坐标是_ ___.
利用图象法解关于x,y的方程组时,若表示两方程的直线重合,则m= ,n= ;若表示两方程的直线平行,则mn= 且n .
若一次函数y=kx+b(k0)的图象经过点A(2021,2020),
B(2020,2019),则 ____(填“是”或“不是”)二元一次方程kx-y+b=0的解.
三、解答题(本大题共3小题,共40分)
在同一直角坐标系中画出一次函数=-2x+2与=x-4的图象,并根据图象解答下列问题:
(1)直线=-2x+2,=x-4与y轴分别相交于点A,B,请写出A,B两点的坐标;
(2)根据图象写出方程组的解;
(3)若与相交于点P,求APB的面积.
如图,直线m:3x+3y=12与x轴交于点A,与y轴交于点B,直线n:ax+by=-5与x轴交于点C,与直线m交于点P,若点P的横坐标为1.
(1)求A,B两点的坐标;
(2)直接写出方程组的解;
(3)求a和b的值;
(4)求三角形PAC的面积.
小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分钟的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度骑行直到到达图书馆.小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图所示.
请结合图象,解答下列问题:
(1)a= ,m= ;
(2)若小军的速度是120米/分钟,求小军在途中与爸爸第二次相遇时,与图书馆之间的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米
(4)若小军的行驶速度是v米/分钟,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
参考答案
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】一
10.【答案】(32,4800)
11.【答案】 -3 -4 -3
12.【答案】是
13.【答案】解:画一次函数=-2x+2与=x-4的图象如图.
(1)由图象可知,A,B两点的坐标分别为A(0,2),B(0,-4).
(2)由图象知,直线=-2x+2与=x-4的交点坐标为(2,-2),
所以方程组的解为
(3)=(2+4)2=6.
14.【答案】解:(1)令3x+3y=12中y=0,则3x=12,
解得x=4,
所以点A的坐标为(4,0).
令3x+3y=12中x=0,则3y=12,
解得y=4,
所以点B的坐标为(0,4).
(2)令3x+3y=12中x=1,则3+3y=12,
解得y=3,
所以点P的坐标为(1,3).
所以方程组的解是
(3)将C,P(1,3)代入ax+by=-5中,得解得
(4)AC=4-=,
所以=3=8.5.
15.【答案】解:(1)爸爸先以150米/分钟的速度骑行1500米,a==10.
爸爸休息了5分钟,b=a+5=10+5=15,m==200.
(2)设线段BC的解析式为y=kx+(k0),
B(15,1500),C(22.5,3000),解得
线段BC的解析式为y=200x-1500(15x22.5).
小军的速度是120米/分钟,
走完3000米所用时间为t==25(分钟),点D的坐标为(25,3000),
设线段OD的函数解析式为y=x(0),则=3000,解得=120.
线段OD的函数解析式为y=120x(0x25).
由题图知,第二次相遇点为OD与BC的交点,联立得解得
OD与BC的交点坐标为(,2250).
小军在途中与爸爸第二次相遇时,与图书馆之间的距离为3000-2250=750(米).
(3)爸爸自第二次出发,所行驶的路程y(米)与时间x(分钟)的函数解析式为y=200x-1500(15x22.5).
当<时,-=100,即120x-(200x-1500)=100,解得x=17.5.
15<17.5<22.5,x=17.5符合题意;
当>时,-=100,即200x-1500-120x=100,解得x=20.
15<20<22.5,x=20符合题意.
综上所述,爸爸自第二次出发至到达图书馆前,在17.5分钟和20分钟时与小军相距100米.
(4)如图,当线段OD过点B时,小军的速度为150015=100(米/分钟);
当线段OD过点C时,小军的速度为300022.5=(米/分钟).
结合图象可知,当100<v<时,小军在途中与爸爸恰好相遇两次(不包括家、图书馆两地).
第2页,共3页
