沪科版2021-2022学年八年级数学上册15.2 线段的垂直平分线 同步测试卷(word版、含答案)
文档属性
| 名称 | 沪科版2021-2022学年八年级数学上册15.2 线段的垂直平分线 同步测试卷(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 175.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 15:17:24 | ||
图片预览

文档简介
15.2 线段的垂直平分线同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共35分)
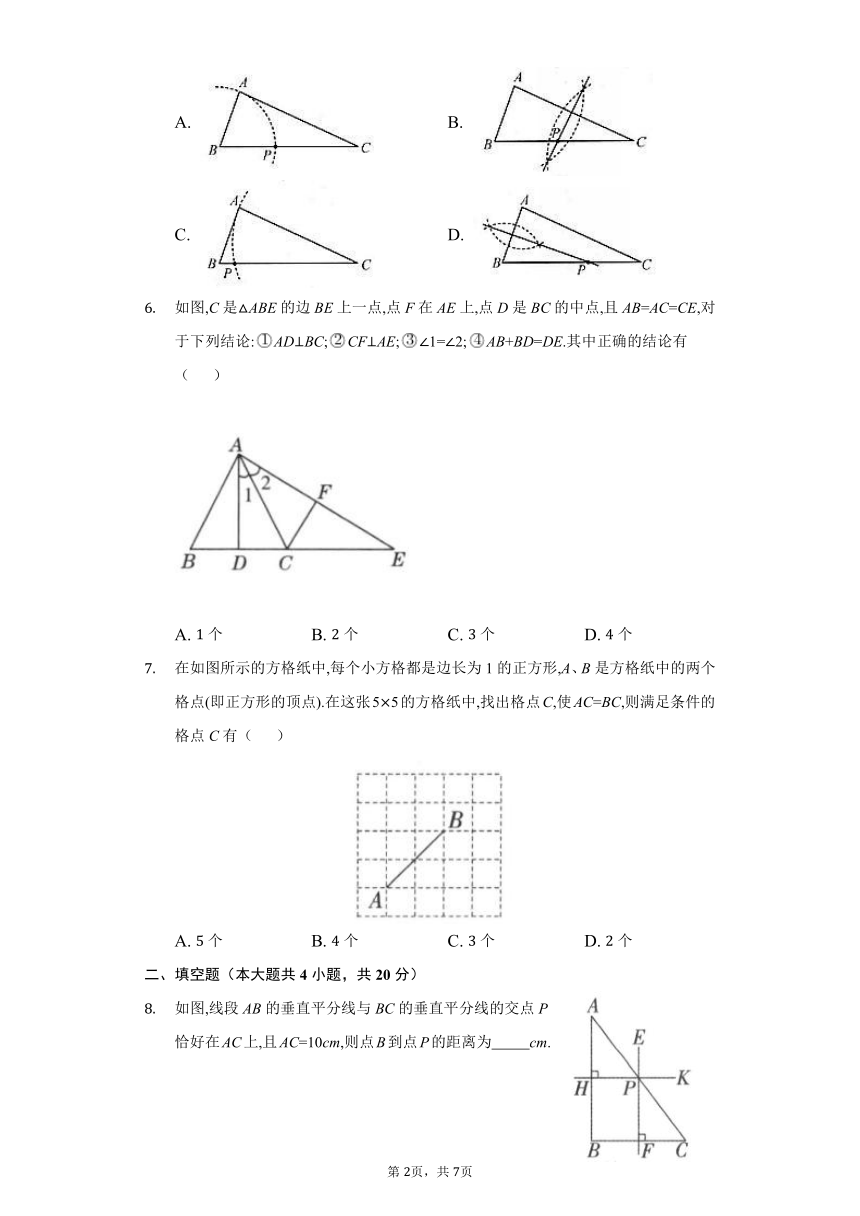
如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.线段PA=5,则线段PB的长为( )
A. B.
C. D.
如图,若AC=AD,BC=BD,则( )
A. 垂直平分 B. 垂直平分
C. 与互相垂直平分 D. 平分
如图,在ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于M,N,作直线MN,交BC于点D,连接AD.如果AD=5,CD=2,那么BC=( )
A. B. C. D.
如图,在ABC中,AB=6,BC=7,AC=4,直线m是ABC中BC边的垂直平分线,点P是直线m上的一动点,则APC周长的最小值为( )
A. B. C. D.
已知ABC(AC< BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
A. B.
C. D.
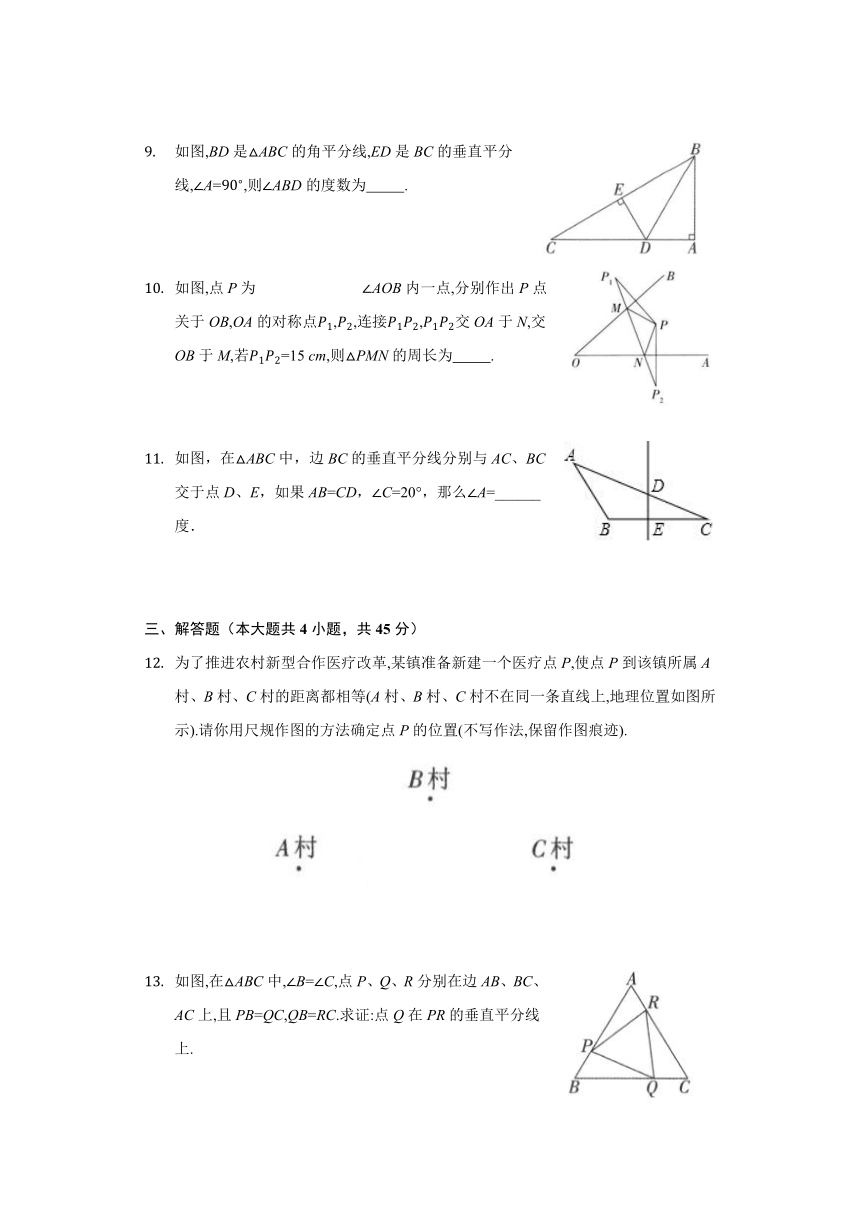
如图,C是ABE的边BE上一点,点F在AE上,点D是BC的中点,且AB=AC=CE,对于下列结论:ADBC;CFAE;1=2;AB+BD=DE.其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
在如图所示的方格纸中,每个小方格都是边长为1的正方形,A、B是方格纸中的两个格点(即正方形的顶点).在这张55的方格纸中,找出格点C,使AC=BC,则满足条件的格点C有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共4小题,共20分)
如图,线段AB的垂直平分线与BC的垂直平分线的交点P恰好在AC上,且AC=10cm,则点B到点P的距离为 cm.
如图,BD是ABC的角平分线,ED是BC的垂直平分线,A=,则ABD的度数为 .
如图,点P为 AOB内一点,分别作出P点关于OB,OA的对称点,,连接,交OA于N,交OB于M,若=15 cm,则PMN的周长为 .
如图,在△ABC中,边BC的垂直平分线分别与AC、BC交于点D、E,如果AB=CD,∠C=20°,那么∠A=______度.
三、解答题(本大题共4小题,共45分)
为了推进农村新型合作医疗改革,某镇准备新建一个医疗点P,使点P到该镇所属A村、B村、C村的距离都相等(A村、B村、C村不在同一条直线上,地理位置如图所示).请你用尺规作图的方法确定点P的位置(不写作法,保留作图痕迹).
如图,在ABC中,B=C,点P、Q、R分别在边AB、BC、AC上,且PB=QC,QB=RC.求证:点Q在PR的垂直平分线上.
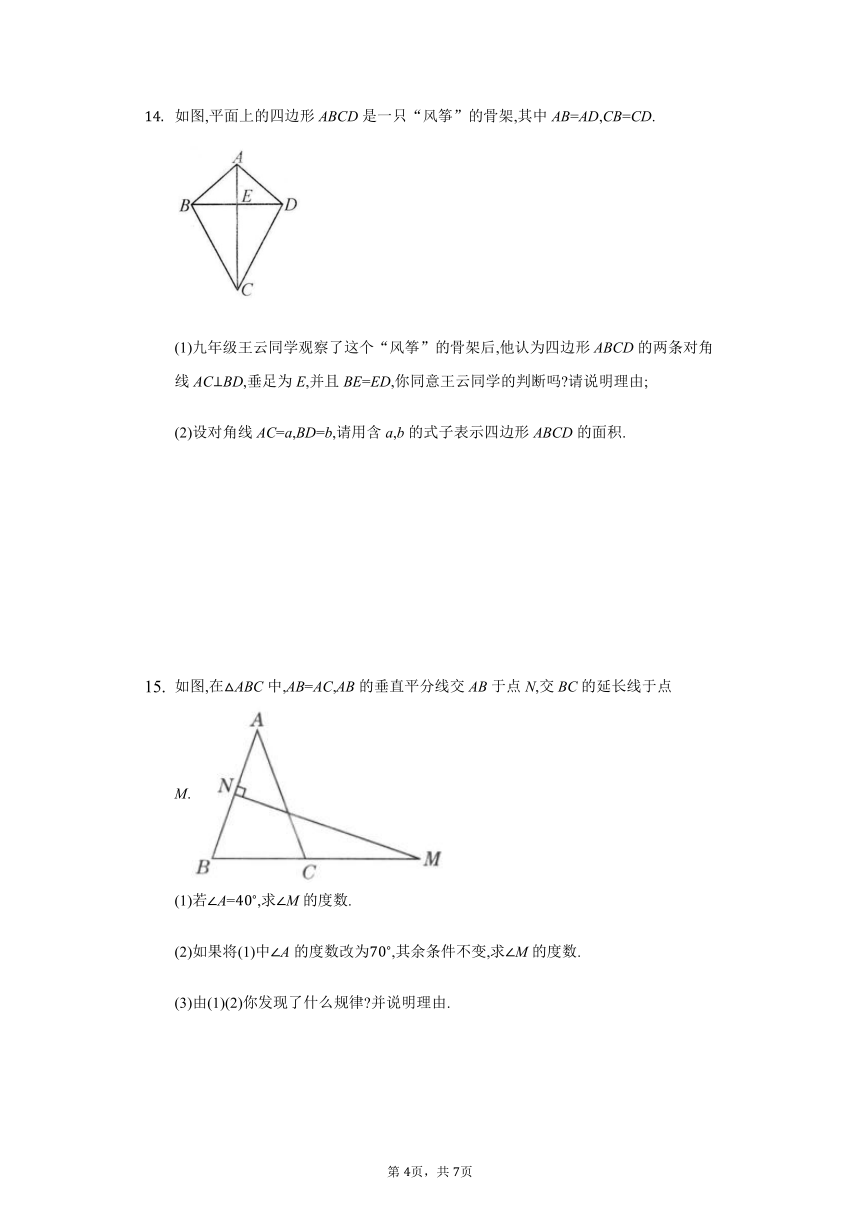
如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD.
(1)九年级王云同学观察了这个“风筝”的骨架后,他认为四边形ABCD的两条对角线ACBD,垂足为E,并且BE=ED,你同意王云同学的判断吗 请说明理由;
(2)设对角线AC=a,BD=b,请用含a,b的式子表示四边形ABCD的面积.
如图,在ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
(1)若A=,求M的度数.
(2)如果将(1)中A的度数改为,其余条件不变,求M的度数.
(3)由(1)(2)你发现了什么规律 并说明理由.
参考答案
1.【答案】D
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】A
8.【答案】5
9.【答案】30°
10.【答案】15 cm
11.【答案】40
12.【答案】解:如图,点P即为所求作.
13.【答案】证明:在BPQ和CQR中,
BPQCQR(SAS).
QP=RQ.
点Q在PR的垂直平分线上.
14.【答案】解:(1)王云同学的判断是正确的.
理由如下:AB=AD,
点A在BD的垂直平分线上.
CB=CD,
点C在BD的垂直平分线上.
AC为BD的垂直平分线.
BE=DE,ACBD.
(2)由(1)得ACBD.
=+
=BDCE+BDAE
=BDAC
=ab.
15.【答案】解:(1)AB=AC,A=,
B=ACB==.
又MN为AB的垂直平分线,
MNAB,MNB=,
M=--B=-=.
(2)过程同(1)可求得M=.
(3)规律:M=A.
理由:连接AM.
在ABC中,AB=AC,
ABC=ACB.
NM垂直平分AB,
BM=AM.
ABC=BAM.
BAM=ACB.
又BAM=BAC+CAM, ACB=CMA+CAM,
BAC=BMA.
易知BMN=AMN,
NMB=BMA=BAC.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共35分)
如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.线段PA=5,则线段PB的长为( )
A. B.
C. D.
如图,若AC=AD,BC=BD,则( )
A. 垂直平分 B. 垂直平分
C. 与互相垂直平分 D. 平分
如图,在ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于M,N,作直线MN,交BC于点D,连接AD.如果AD=5,CD=2,那么BC=( )
A. B. C. D.
如图,在ABC中,AB=6,BC=7,AC=4,直线m是ABC中BC边的垂直平分线,点P是直线m上的一动点,则APC周长的最小值为( )
A. B. C. D.
已知ABC(AC< BC),用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )
A. B.
C. D.
如图,C是ABE的边BE上一点,点F在AE上,点D是BC的中点,且AB=AC=CE,对于下列结论:ADBC;CFAE;1=2;AB+BD=DE.其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
在如图所示的方格纸中,每个小方格都是边长为1的正方形,A、B是方格纸中的两个格点(即正方形的顶点).在这张55的方格纸中,找出格点C,使AC=BC,则满足条件的格点C有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共4小题,共20分)
如图,线段AB的垂直平分线与BC的垂直平分线的交点P恰好在AC上,且AC=10cm,则点B到点P的距离为 cm.
如图,BD是ABC的角平分线,ED是BC的垂直平分线,A=,则ABD的度数为 .
如图,点P为 AOB内一点,分别作出P点关于OB,OA的对称点,,连接,交OA于N,交OB于M,若=15 cm,则PMN的周长为 .
如图,在△ABC中,边BC的垂直平分线分别与AC、BC交于点D、E,如果AB=CD,∠C=20°,那么∠A=______度.
三、解答题(本大题共4小题,共45分)
为了推进农村新型合作医疗改革,某镇准备新建一个医疗点P,使点P到该镇所属A村、B村、C村的距离都相等(A村、B村、C村不在同一条直线上,地理位置如图所示).请你用尺规作图的方法确定点P的位置(不写作法,保留作图痕迹).
如图,在ABC中,B=C,点P、Q、R分别在边AB、BC、AC上,且PB=QC,QB=RC.求证:点Q在PR的垂直平分线上.
如图,平面上的四边形ABCD是一只“风筝”的骨架,其中AB=AD,CB=CD.
(1)九年级王云同学观察了这个“风筝”的骨架后,他认为四边形ABCD的两条对角线ACBD,垂足为E,并且BE=ED,你同意王云同学的判断吗 请说明理由;
(2)设对角线AC=a,BD=b,请用含a,b的式子表示四边形ABCD的面积.
如图,在ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
(1)若A=,求M的度数.
(2)如果将(1)中A的度数改为,其余条件不变,求M的度数.
(3)由(1)(2)你发现了什么规律 并说明理由.
参考答案
1.【答案】D
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】D
6.【答案】B
7.【答案】A
8.【答案】5
9.【答案】30°
10.【答案】15 cm
11.【答案】40
12.【答案】解:如图,点P即为所求作.
13.【答案】证明:在BPQ和CQR中,
BPQCQR(SAS).
QP=RQ.
点Q在PR的垂直平分线上.
14.【答案】解:(1)王云同学的判断是正确的.
理由如下:AB=AD,
点A在BD的垂直平分线上.
CB=CD,
点C在BD的垂直平分线上.
AC为BD的垂直平分线.
BE=DE,ACBD.
(2)由(1)得ACBD.
=+
=BDCE+BDAE
=BDAC
=ab.
15.【答案】解:(1)AB=AC,A=,
B=ACB==.
又MN为AB的垂直平分线,
MNAB,MNB=,
M=--B=-=.
(2)过程同(1)可求得M=.
(3)规律:M=A.
理由:连接AM.
在ABC中,AB=AC,
ABC=ACB.
NM垂直平分AB,
BM=AM.
ABC=BAM.
BAM=ACB.
又BAM=BAC+CAM, ACB=CMA+CAM,
BAC=BMA.
易知BMN=AMN,
NMB=BMA=BAC.
第2页,共2页
