沪科版2021-2022学年八年级数学上册15.3 等腰三角形 同步测试卷(word版、含答案)
文档属性
| 名称 | 沪科版2021-2022学年八年级数学上册15.3 等腰三角形 同步测试卷(word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 244.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 15:18:59 | ||
图片预览



文档简介
15.3 等腰三角形同步测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共16小题,共48分)
如图,在ABC中,AB=AC,A=,CDAB,则BCD=( )
A. B. C. D.
如图,在ABC中,AB=AC,ADBC,以下结论中错误的是( )
A.
B.
C. 为的中点
D. 是的角平分线
若等腰三角形的一个内角为,则另外两个内角的度数分别是( )
A. , B. ,或,
C. , D. ,或,
“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”(图为图的示意图)能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若BDE=,则CDE的度数是( )
A. B. C. D.
如图,已知等腰ABC,AB=AC,若以点B为圆心,BC的长为半径画弧,交腰AC于点E,连接BE,则下列结论一定正确的是( )
A. B.
C. D.
下列条件中,不能判定ABC是等腰三角形的是( )
A. ,, B.
C. , D.
如图,直线分别与直线AB,CD相交于点E,F,EG平分BEF交直线CD于点G.若1=BEF,EF=3,则FG=( )
A. B. C. D.
如图,上午8时,一艘船从海岛A出发,以15 n mile/h的速度向正北方向航行,10时到达海岛B处,分别从A,B处观测灯塔C,测得NAC=,NBC=,则从海岛B到灯塔C的距离为( )
A. B.
C. D.
在如图所示的三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A. B. C. D.
如图,B=C=,ADE=AED=,则图中的等腰三角形有( )
A. 个 B. 个 C. 个 D. 个
如图所示,一场暴雨过后,垂直于地面的一棵树在距地面3米处折断,树尖B恰好碰到地面,经测量ABC=,则树高为( )
A. 米 B. 米 C. 米 D. 米
如图,在ABC中,ACB=,CDAB于点D,A=,以下说法错误的是( )
A. B.
C. D.
如图,在ABC中,AB=AC,C=,ABAD,AD=4 cm,则BC的长为( )
A. B.
C. D.
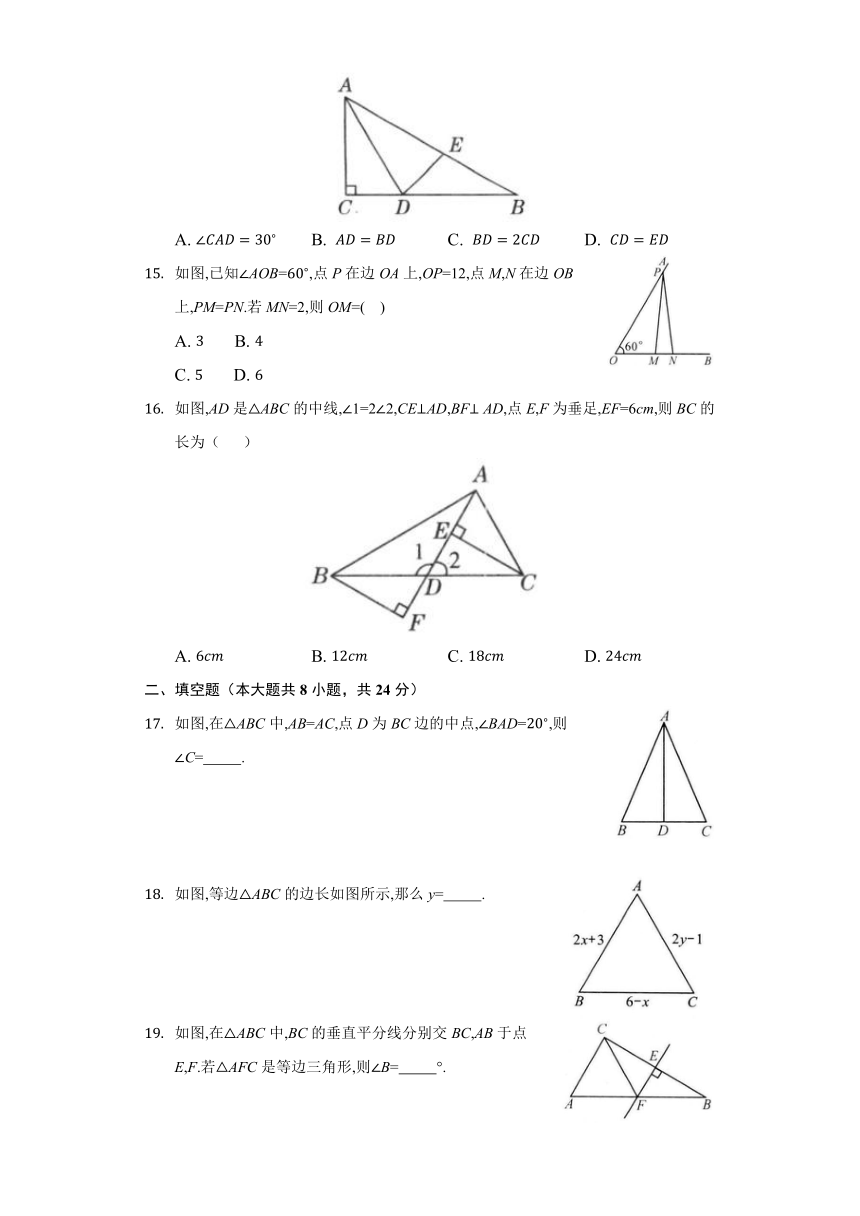
如图,在ABC中,C=,B=,AD平分CAB交BC于点D,E为AB上一点,连接DE,则下列说法错误的是( )
A. B. C. D.
如图,已知AOB=,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=( )
A. B.
C. D.
如图,AD是ABC的中线,1=22,CEAD,BF AD,点E,F为垂足,EF=6cm,则BC的长为( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
如图,在ABC中,AB=AC,点D为BC边的中点,BAD=,则C= .
如图,等边ABC的边长如图所示,那么y= .
如图,在ABC中,BC的垂直平分线分别交BC,AB于点E,F.若AFC是等边三角形,则B= °.
如图,在一个池塘两旁有一条笔直的小路(B,C为小路端点)和一棵小树(A为小树的位置),测得的相关数据为ABC=,ACB=,BC=48米,则AC= 米.
在下列命题中:有一个角是的等腰三角形是等边三角形;有两个外角相等的等腰三角形是等边三角形;一边上的高也是这边上的中线的等腰三角形是等边三角形;三个外角都相等的三角形是等边三角形.其中正确的是 .(只需填写序号)
如图,在ABC中,AB=6 cm,A=,分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于两点,过这两点的直线交AC于点D,连接BD,则ABD的周长为 cm.
如图,在ABC中,C=,B=,AD平分CAB,交BC于点D.若CD=1,则BD= .
如图,在ABC中,B=,ED垂直平分BC,ED=3,则CE的长为 .
三、解答题(本大题共6小题,共48分)
如图,在等边三角形ABC中,BD是ABC的角平分线,延长BC到点E,使CE=CD,AB=6 cm.
求:(1)E的度数;
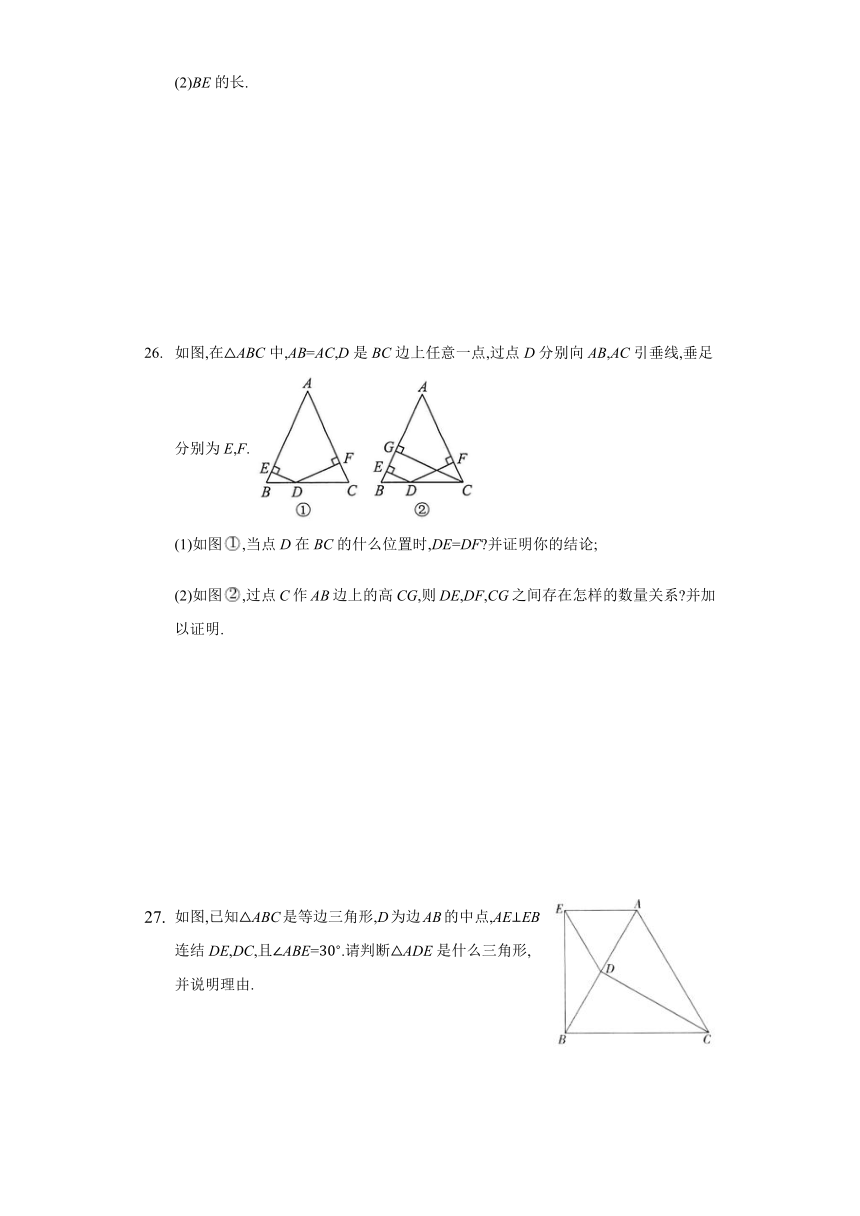
(2)BE的长.
如图,在ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图,当点D在BC的什么位置时,DE=DF 并证明你的结论;
(2)如图,过点C作AB边上的高CG,则DE,DF,CG之间存在怎样的数量关系 并加以证明.
如图,已知ABC是等边三角形,D为边AB的中点,AEEB,连结DE,DC,且ABE=.请判断ADE是什么三角形,并说明理由.
如图,点E在ABC的AC边的延长线上,点D在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:ABC是等腰三角形.
如图,在ABC中,AB=AC,BAC=,D为BC的中点,DEAC于点E,AE=8,求CE的长.
如图,在ABC中,A=,ABC=,BC的垂直平分线交BC于点D,交AC于点E.
(1)求证:AE=DE;
(2)若AE=6,求CE的长.
参考答案
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】B
9.【答案】D
10.【答案】D
11.【答案】B
12.【答案】B
13.【答案】B
14.【答案】D
15.【答案】C
16.【答案】B
17.【答案】
18.【答案】3
19.【答案】30
20.【答案】48
21.【答案】
22.【答案】18
23.【答案】2
24.【答案】6
25.【答案】解:(1) ;
(2)9 cm.
26.【答案】解:(1)当D是BC的中点时,DE=DF.
证明:AB=AC,B=C.
DEAB,DFAC,
DEB=DFC.
D是BC的中点,BD=CD.
在DEB和DFC中,
DEBDFC.
DE=DF.
(2)DE+DF=CG.
证明:如图,连接AD.
由题意,知 =ABDE,=ACDF,=ABCG.
+=,
ABDE+ACDF=ABCG.
又AB=AC,
DE+DF=CG.
27.【答案】ADE为等边三角形.
理由:ABC为等边三角形,
AB=BC=AC,BAC=,
D是AB的中点,
CDAB,
AEEB,
ADC=AEB=,
ABE=,BAE=,
BAE=BAC,
在ADC和AEB中,
ADCAEB(AAS),
AE=AD,
BAE=,
ADE是等边三角形.
28.【答案】证明:过点D作DGAC交BC于点G,如图所示.
DGAC,
GDF=E,DGB=ACB.
在GDF和CEF中,
GDFCEF(ASA),
GD=CE.
BD=CE,BD=GD,
B=DGB,
B=ACB,
则AB=AC,
ABC是等腰三角形.
29.【答案】解:连接AD,
AB=AC,BAC=,D为BC的中点,
ADBC,AD平分BAC,B=C=.
DAC=BAC=.
DEAC于点E,
AED=.
ADE=.
在RtADE中,AE=8,ADE=,
AD=2AE=16.
在RtADC中,AD=16,C=,
AC=2AD=32.
CE=AC-AE=32-8=24.
30.【答案】解:(1)证明:连接BE,
A=,ABC=,
C=.
BC的垂直平分线交BC于点D,交AC于点E,
BE=CE.
C=EBC=.
ABE=.
AE=BE,DE=BE.
AE=DE.
(2)12.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共16小题,共48分)
如图,在ABC中,AB=AC,A=,CDAB,则BCD=( )
A. B. C. D.
如图,在ABC中,AB=AC,ADBC,以下结论中错误的是( )
A.
B.
C. 为的中点
D. 是的角平分线
若等腰三角形的一个内角为,则另外两个内角的度数分别是( )
A. , B. ,或,
C. , D. ,或,
“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”(图为图的示意图)能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若BDE=,则CDE的度数是( )
A. B. C. D.
如图,已知等腰ABC,AB=AC,若以点B为圆心,BC的长为半径画弧,交腰AC于点E,连接BE,则下列结论一定正确的是( )
A. B.
C. D.
下列条件中,不能判定ABC是等腰三角形的是( )
A. ,, B.
C. , D.
如图,直线分别与直线AB,CD相交于点E,F,EG平分BEF交直线CD于点G.若1=BEF,EF=3,则FG=( )
A. B. C. D.
如图,上午8时,一艘船从海岛A出发,以15 n mile/h的速度向正北方向航行,10时到达海岛B处,分别从A,B处观测灯塔C,测得NAC=,NBC=,则从海岛B到灯塔C的距离为( )
A. B.
C. D.
在如图所示的三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
A. B. C. D.
如图,B=C=,ADE=AED=,则图中的等腰三角形有( )
A. 个 B. 个 C. 个 D. 个
如图所示,一场暴雨过后,垂直于地面的一棵树在距地面3米处折断,树尖B恰好碰到地面,经测量ABC=,则树高为( )
A. 米 B. 米 C. 米 D. 米
如图,在ABC中,ACB=,CDAB于点D,A=,以下说法错误的是( )
A. B.
C. D.
如图,在ABC中,AB=AC,C=,ABAD,AD=4 cm,则BC的长为( )
A. B.
C. D.
如图,在ABC中,C=,B=,AD平分CAB交BC于点D,E为AB上一点,连接DE,则下列说法错误的是( )
A. B. C. D.
如图,已知AOB=,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=( )
A. B.
C. D.
如图,AD是ABC的中线,1=22,CEAD,BF AD,点E,F为垂足,EF=6cm,则BC的长为( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
如图,在ABC中,AB=AC,点D为BC边的中点,BAD=,则C= .
如图,等边ABC的边长如图所示,那么y= .
如图,在ABC中,BC的垂直平分线分别交BC,AB于点E,F.若AFC是等边三角形,则B= °.
如图,在一个池塘两旁有一条笔直的小路(B,C为小路端点)和一棵小树(A为小树的位置),测得的相关数据为ABC=,ACB=,BC=48米,则AC= 米.
在下列命题中:有一个角是的等腰三角形是等边三角形;有两个外角相等的等腰三角形是等边三角形;一边上的高也是这边上的中线的等腰三角形是等边三角形;三个外角都相等的三角形是等边三角形.其中正确的是 .(只需填写序号)
如图,在ABC中,AB=6 cm,A=,分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于两点,过这两点的直线交AC于点D,连接BD,则ABD的周长为 cm.
如图,在ABC中,C=,B=,AD平分CAB,交BC于点D.若CD=1,则BD= .
如图,在ABC中,B=,ED垂直平分BC,ED=3,则CE的长为 .
三、解答题(本大题共6小题,共48分)
如图,在等边三角形ABC中,BD是ABC的角平分线,延长BC到点E,使CE=CD,AB=6 cm.
求:(1)E的度数;
(2)BE的长.
如图,在ABC中,AB=AC,D是BC边上任意一点,过点D分别向AB,AC引垂线,垂足分别为E,F.
(1)如图,当点D在BC的什么位置时,DE=DF 并证明你的结论;
(2)如图,过点C作AB边上的高CG,则DE,DF,CG之间存在怎样的数量关系 并加以证明.
如图,已知ABC是等边三角形,D为边AB的中点,AEEB,连结DE,DC,且ABE=.请判断ADE是什么三角形,并说明理由.
如图,点E在ABC的AC边的延长线上,点D在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:ABC是等腰三角形.
如图,在ABC中,AB=AC,BAC=,D为BC的中点,DEAC于点E,AE=8,求CE的长.
如图,在ABC中,A=,ABC=,BC的垂直平分线交BC于点D,交AC于点E.
(1)求证:AE=DE;
(2)若AE=6,求CE的长.
参考答案
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】B
9.【答案】D
10.【答案】D
11.【答案】B
12.【答案】B
13.【答案】B
14.【答案】D
15.【答案】C
16.【答案】B
17.【答案】
18.【答案】3
19.【答案】30
20.【答案】48
21.【答案】
22.【答案】18
23.【答案】2
24.【答案】6
25.【答案】解:(1) ;
(2)9 cm.
26.【答案】解:(1)当D是BC的中点时,DE=DF.
证明:AB=AC,B=C.
DEAB,DFAC,
DEB=DFC.
D是BC的中点,BD=CD.
在DEB和DFC中,
DEBDFC.
DE=DF.
(2)DE+DF=CG.
证明:如图,连接AD.
由题意,知 =ABDE,=ACDF,=ABCG.
+=,
ABDE+ACDF=ABCG.
又AB=AC,
DE+DF=CG.
27.【答案】ADE为等边三角形.
理由:ABC为等边三角形,
AB=BC=AC,BAC=,
D是AB的中点,
CDAB,
AEEB,
ADC=AEB=,
ABE=,BAE=,
BAE=BAC,
在ADC和AEB中,
ADCAEB(AAS),
AE=AD,
BAE=,
ADE是等边三角形.
28.【答案】证明:过点D作DGAC交BC于点G,如图所示.
DGAC,
GDF=E,DGB=ACB.
在GDF和CEF中,
GDFCEF(ASA),
GD=CE.
BD=CE,BD=GD,
B=DGB,
B=ACB,
则AB=AC,
ABC是等腰三角形.
29.【答案】解:连接AD,
AB=AC,BAC=,D为BC的中点,
ADBC,AD平分BAC,B=C=.
DAC=BAC=.
DEAC于点E,
AED=.
ADE=.
在RtADE中,AE=8,ADE=,
AD=2AE=16.
在RtADC中,AD=16,C=,
AC=2AD=32.
CE=AC-AE=32-8=24.
30.【答案】解:(1)证明:连接BE,
A=,ABC=,
C=.
BC的垂直平分线交BC于点D,交AC于点E,
BE=CE.
C=EBC=.
ABE=.
AE=BE,DE=BE.
AE=DE.
(2)12.
第2页,共3页
