人教版 2020—2021学年九年级数学下册28.1 锐角三角函数——余弦和正切同步练习(word版、含答案)
文档属性
| 名称 | 人教版 2020—2021学年九年级数学下册28.1 锐角三角函数——余弦和正切同步练习(word版、含答案) | 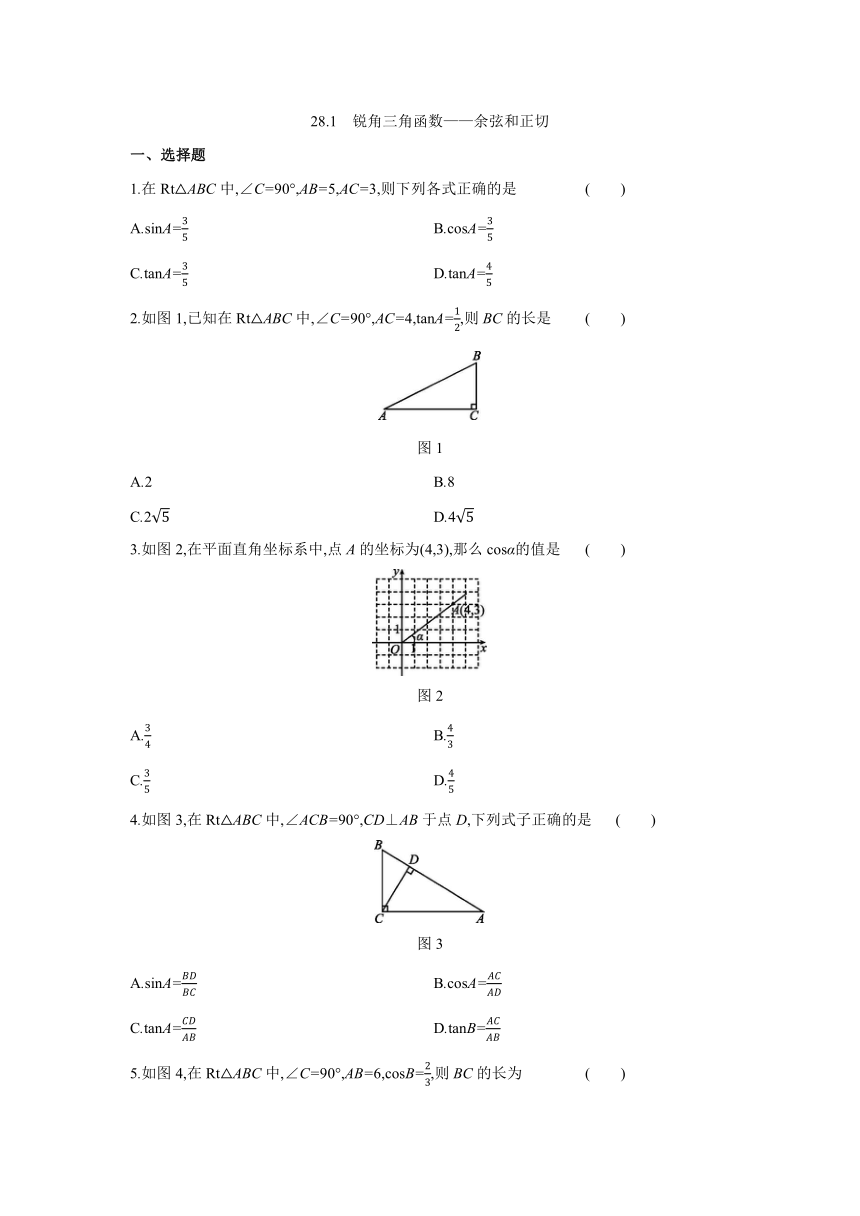 | |
| 格式 | docx | ||
| 文件大小 | 194.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 15:22:49 | ||
图片预览




文档简介
28.1 锐角三角函数——余弦和正切
一、选择题
1.在Rt△ABC中,∠C=90°,AB=5,AC=3,则下列各式正确的是 ( )
A.sinA= B.cosA=
C.tanA= D.tanA=
2.如图1,已知在Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是 ( )
图1
A.2 B.8
C.2 D.4
3.如图2,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是 ( )
图2
A. B.
C. D.
4.如图3,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列式子正确的是 ( )
图3
A.sinA= B.cosA=
C.tanA= D.tanB=
5.如图4,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为 ( )
图4
A.4 B.2
C. D.
6.如图5,在△ABC中,∠C=90°,tanA=2,则cosA的值为 ( )
图5
A. B. C. D.
7.[2020·凉山州] 如图6所示,△ABC的顶点都在正方形网格的格点上,则tanA的值为( )
图6
A. B. C.2 D.2
8.如图7,半径为3的☉A经过原点O和点C(0,2),B是y轴左侧☉A上的一点,则tan∠OBC的值为 ( )
图7
A. B.2 C. D.
9.如图8,在△ABC中,AC⊥BC,∠ABC=30°,D是CB延长线上的一点,且BD=AB,则tanD的值为 ( )
图8
A.2 B.3 C.2+ D.2-
二、填空题
10.在Rt△ABC中,∠C=90°,tanA=,BC=8,则△ABC的面积为 .
11.在△ABC中,∠C=90°,tanA=,则cosB= .
12.如图9所示,在平面直角坐标系中,已知点A的坐标为(2,0),点B的坐标为(0,4),且∠1=∠2,则tan∠OCA= .
图9
13.[2020·扬州] 如图10,在由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为 .
图10
三、解答题
14.如图11,在Rt△ABC中,∠C=90°,tanA=,求sinA和cosA的值.
图11
15.如图12,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
图12
16.[2020·杭州改编] 如图13所示,已知AB是☉O的直径,∠ABC=90°,连接AC,OC.若sin∠BAC=,求sin∠BOC,cos∠BOC和tan∠BOC的值.
图13
17.如图14,已知AB是☉O的直径,点C,D在☉O上,且AB=5,BC=3.
(1)求sin∠BAC的值;
(2)如果OE⊥AC,垂足为E,求OE的长;
(3)求tan∠ADC的值.
图14
答案
1.B 2.A
3.D [解析]由勾股定理得OA==5,所以cosα=.故选D.
4.A [解析]∵∠ACB=90°,CD⊥AB,
∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,
∴∠A=∠BCD,
则sinA=sin∠BCD=.
5.A [解析]∵cosB=,∴=.∵AB=6,
∴BC=×6=4.故选A.
6.B [解析]∵在△ABC中,∠C=90°,
∴tanA==2,∴设BC=2k,AC=k,
∴AB==k,
∴cosA===.
7.A [解析]如图,取格点D,连接BD.设小正方形的边长均为1,由勾股定理,得DB=,AD=2,AB=,则AD2+DB2=AB2,所以△ABD是直角三角形,且∠ADB=90°,所以在Rt△ADB中,tanA===.故选A.
8.D [解析]如图,设☉A与x轴的另一个交点为D,连接CD.
因为∠COD=90°,所以CD为☉A的直径.
在Rt△OCD中,CD=6,OC=2,
则OD==4,
所以tan∠CDO==.
由圆周角定理,得∠OBC=∠CDO,
则tan∠OBC=tan∠CDO=.
9.D [解析]法一:设AC=m.
在Rt△ABC中,∵∠C=90°,∠ABC=30°,
∴AB=2AC=2m,
∴BD=AB=2m,BC==m,
则CD=2m+m,
∴tanD===2-.
法二:可用特殊值法,取AC=1,然后分别计算需要的边长求值即可.
10.24
11. [解析]∵在Rt△ABC中,∠C=90°,tanA=,
∴可设BC=x,AC=3x,则AB=2x,
∴cosB==.
12.2 [解析]∵∠1=∠2,∠1+∠OCA=∠2+∠BAO=90°,∴∠OCA=∠BAO.
∵A(2,0),B(0,4),
∴tan∠OCA=tan∠BAO==2.
13. [解析]如图,连接AC,BC.
∵∠ADC和∠ABC所对的弧都是,
∴根据圆周角定理知,∠ADC=∠ABC.
∵AB是圆的直径,
∴∠ACB=90°,
∴在Rt△ACB中,根据锐角三角函数的定义知,sin∠ABC=.
∵AC=2,CB=3,∴AB=,
∴sin∠ABC==,
∴sin∠ADC=sin∠ABC=.
14.解:∵tanA==,
故设BC=2k,AC=3k,
∴AB===k,
∴sinA===,
cosA===.
15.解:在Rt△ACD中,CD=6,tanA=,
∴AD=4,
∴BD=AB-AD=8.
在Rt△BCD中,由勾股定理,得BC==10,
∴sinB==,cosB==,
∴sinB+cosB=+=.
16.解:∵AB是☉O的直径,∠ABC=90°,
sin∠BAC==,
∴可设BC=x,AC=3x,
则AB===2x,
∴OB=AB=x,
∴OC==x,
∴sin∠BOC===,cos∠BOC===,tan∠BOC===.
17.解:(1)∵AB是☉O的直径,
∴∠ACB=90°.
∵AB=5,BC=3,
∴sin∠BAC==.
(2)∵OE⊥AC,∠ACB=90°,
∴OE∥BC.
又∵O是AB的中点,
∴OE是△ABC的中位线,
∴OE=BC=.
(3)∵AC==4,
∴tan∠ADC=tan∠ABC==.
一、选择题
1.在Rt△ABC中,∠C=90°,AB=5,AC=3,则下列各式正确的是 ( )
A.sinA= B.cosA=
C.tanA= D.tanA=
2.如图1,已知在Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是 ( )
图1
A.2 B.8
C.2 D.4
3.如图2,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是 ( )
图2
A. B.
C. D.
4.如图3,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列式子正确的是 ( )
图3
A.sinA= B.cosA=
C.tanA= D.tanB=
5.如图4,在Rt△ABC中,∠C=90°,AB=6,cosB=,则BC的长为 ( )
图4
A.4 B.2
C. D.
6.如图5,在△ABC中,∠C=90°,tanA=2,则cosA的值为 ( )
图5
A. B. C. D.
7.[2020·凉山州] 如图6所示,△ABC的顶点都在正方形网格的格点上,则tanA的值为( )
图6
A. B. C.2 D.2
8.如图7,半径为3的☉A经过原点O和点C(0,2),B是y轴左侧☉A上的一点,则tan∠OBC的值为 ( )
图7
A. B.2 C. D.
9.如图8,在△ABC中,AC⊥BC,∠ABC=30°,D是CB延长线上的一点,且BD=AB,则tanD的值为 ( )
图8
A.2 B.3 C.2+ D.2-
二、填空题
10.在Rt△ABC中,∠C=90°,tanA=,BC=8,则△ABC的面积为 .
11.在△ABC中,∠C=90°,tanA=,则cosB= .
12.如图9所示,在平面直角坐标系中,已知点A的坐标为(2,0),点B的坐标为(0,4),且∠1=∠2,则tan∠OCA= .
图9
13.[2020·扬州] 如图10,在由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则sin∠ADC的值为 .
图10
三、解答题
14.如图11,在Rt△ABC中,∠C=90°,tanA=,求sinA和cosA的值.
图11
15.如图12,在△ABC中,CD⊥AB,垂足为D.若AB=12,CD=6,tanA=,求sinB+cosB的值.
图12
16.[2020·杭州改编] 如图13所示,已知AB是☉O的直径,∠ABC=90°,连接AC,OC.若sin∠BAC=,求sin∠BOC,cos∠BOC和tan∠BOC的值.
图13
17.如图14,已知AB是☉O的直径,点C,D在☉O上,且AB=5,BC=3.
(1)求sin∠BAC的值;
(2)如果OE⊥AC,垂足为E,求OE的长;
(3)求tan∠ADC的值.
图14
答案
1.B 2.A
3.D [解析]由勾股定理得OA==5,所以cosα=.故选D.
4.A [解析]∵∠ACB=90°,CD⊥AB,
∴∠A+∠DCA=90°,∠DCA+∠BCD=90°,
∴∠A=∠BCD,
则sinA=sin∠BCD=.
5.A [解析]∵cosB=,∴=.∵AB=6,
∴BC=×6=4.故选A.
6.B [解析]∵在△ABC中,∠C=90°,
∴tanA==2,∴设BC=2k,AC=k,
∴AB==k,
∴cosA===.
7.A [解析]如图,取格点D,连接BD.设小正方形的边长均为1,由勾股定理,得DB=,AD=2,AB=,则AD2+DB2=AB2,所以△ABD是直角三角形,且∠ADB=90°,所以在Rt△ADB中,tanA===.故选A.
8.D [解析]如图,设☉A与x轴的另一个交点为D,连接CD.
因为∠COD=90°,所以CD为☉A的直径.
在Rt△OCD中,CD=6,OC=2,
则OD==4,
所以tan∠CDO==.
由圆周角定理,得∠OBC=∠CDO,
则tan∠OBC=tan∠CDO=.
9.D [解析]法一:设AC=m.
在Rt△ABC中,∵∠C=90°,∠ABC=30°,
∴AB=2AC=2m,
∴BD=AB=2m,BC==m,
则CD=2m+m,
∴tanD===2-.
法二:可用特殊值法,取AC=1,然后分别计算需要的边长求值即可.
10.24
11. [解析]∵在Rt△ABC中,∠C=90°,tanA=,
∴可设BC=x,AC=3x,则AB=2x,
∴cosB==.
12.2 [解析]∵∠1=∠2,∠1+∠OCA=∠2+∠BAO=90°,∴∠OCA=∠BAO.
∵A(2,0),B(0,4),
∴tan∠OCA=tan∠BAO==2.
13. [解析]如图,连接AC,BC.
∵∠ADC和∠ABC所对的弧都是,
∴根据圆周角定理知,∠ADC=∠ABC.
∵AB是圆的直径,
∴∠ACB=90°,
∴在Rt△ACB中,根据锐角三角函数的定义知,sin∠ABC=.
∵AC=2,CB=3,∴AB=,
∴sin∠ABC==,
∴sin∠ADC=sin∠ABC=.
14.解:∵tanA==,
故设BC=2k,AC=3k,
∴AB===k,
∴sinA===,
cosA===.
15.解:在Rt△ACD中,CD=6,tanA=,
∴AD=4,
∴BD=AB-AD=8.
在Rt△BCD中,由勾股定理,得BC==10,
∴sinB==,cosB==,
∴sinB+cosB=+=.
16.解:∵AB是☉O的直径,∠ABC=90°,
sin∠BAC==,
∴可设BC=x,AC=3x,
则AB===2x,
∴OB=AB=x,
∴OC==x,
∴sin∠BOC===,cos∠BOC===,tan∠BOC===.
17.解:(1)∵AB是☉O的直径,
∴∠ACB=90°.
∵AB=5,BC=3,
∴sin∠BAC==.
(2)∵OE⊥AC,∠ACB=90°,
∴OE∥BC.
又∵O是AB的中点,
∴OE是△ABC的中位线,
∴OE=BC=.
(3)∵AC==4,
∴tan∠ADC=tan∠ABC==.
