人教版2021——2022学年九年级数学下册28.2.1解直角三角形同步练习 (word版、含答案)
文档属性
| 名称 | 人教版2021——2022学年九年级数学下册28.2.1解直角三角形同步练习 (word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 15:25:38 | ||
图片预览



文档简介
28.2.1解直角三角形
一、选择题
1.[2021·云南] 在△ABC中,∠ABC=90°,若AC=100,sinA=,则AB的长是 ( )
A. B.
C.60 D.80
2.[2020·杭州] 如图1,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则 ( )
图1
A.c=bsinB B.b=csinB
C.a=btanB D.b=ctanB
3.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A的度数为 ( )
A.90° B.60°
C.45° D.30°
4.在直角三角形中,下列条件中不能解直角三角形的是 ( )
A.已知一直角边和一锐角
B.已知斜边和一锐角
C.已知两边
D.已知两角
5.如图2,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是 ( )
图2
A. B.12
C.14 D.21
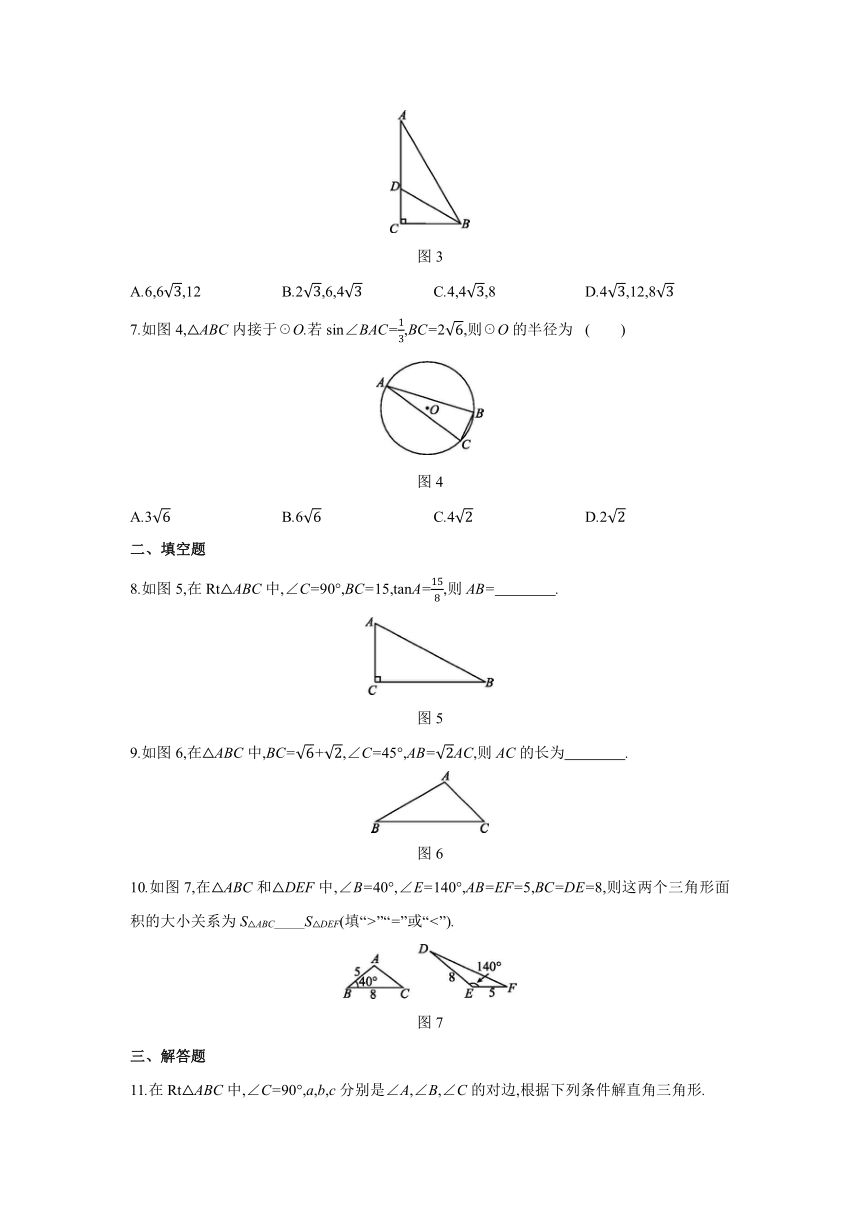
6.如图3,在△ABC中,∠C=90°,∠A=30°.若BD是△ABC的角平分线,BD=8,则△ABC的三边长分别是 ( )
图3
A.6,6,12 B.2,6,4 C.4,4,8 D.4,12,8
7.如图4,△ABC内接于☉O.若sin∠BAC=,BC=2,则☉O的半径为 ( )
图4
A.3 B.6 C.4 D.2
二、填空题
8.如图5,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB= .
图5
9.如图6,在△ABC中,BC=+,∠C=45°,AB=AC,则AC的长为 .
图6
10.如图7,在△ABC和△DEF中,∠B=40°,∠E=140°,AB=EF=5,BC=DE=8,则这两个三角形面积的大小关系为S△ABC S△DEF(填“>”“=”或“<”).
图7
三、解答题
11.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据下列条件解直角三角形.
(1)b=10,∠A=60°;
(2)a=2,b=2 .
12.[2020·安徽改编] 如图8,在Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA=,求BD的长度.
图8
13.[2020·盐城] 如图9,在Rt△ABC中,∠C=90°,tanA=,∠ABC的平分线BD交AC于点D,CD=.求AB的长.
图9
14.如图10,AD是△ABC的中线,tanB=,cosC=,AC=.
求:(1)BC的长;
(2)sin∠ADC的值.
图10
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢 如图11,在锐角三角形ABC中,∠A,∠B,∠ACB所对的边分别为a,b,c(注:sin2A+cos2A=1),过点C作CD⊥AB于点D,在Rt△ADC中,CD=bsinA,AD=bcosA,∴BD=c-bcosA.
在Rt△BDC中,由勾股定理,得CD2+BD2=BC2,
即(bsinA)2+(c-bcosA)2=a2,
整理,得a2=b2+c2-2bccosA.
同理可得b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
(注:上述三个公式对直角三角形和钝角三角形也成立,推理过程同上)
利用上述结论解答下列问题:
(1)在△ABC中,∠A=45°,b=2,c=2,求a的长和∠C的度数;
(2)在△ABC中,a=,b=,∠B=45°,c>a>b,求c的长.
图11
答案
1.D 2.B 3.D 4.D
5.A [解析]如图,过点A作AD⊥BC于点D.
∵在△ABC中,cosB=,
∴∠B=45°,∴BD=AD.
∵sinC==,AC=5,
∴=,
∴AD=3,∴CD=4,BD=3,
则△ABC的面积是·AD·BC=×3×(3+4)=.
6.D [解析]∵∠A=30°,∠C=90°,
∴∠ABC=60°.
∵BD是△ABC的角平分线,
∴∠CBD=30°.
解Rt△BCD,Rt△ABC,即可得△ABC的三边长.
7.A [解析]如图,连接OB,OC,过点O作OD⊥BC于点D,
则∠COD=∠COB=∠BAC,CD=BC=,
∴sin∠COD=sin∠BAC=.又sin∠COD=,
∴=,即=.
∴OC=3.故选A.
8.17 [解析]∵在Rt△ABC中,∠C=90°,tanA==,BC=15,∴=,解得AC=8.根据勾股定理,得AB===17.故答案为17.
9.2 [解析]过点A作AD⊥BC,垂足为D,如图所示.
设AC=x,则AB=x.
在Rt△ACD中,AD=AC·sinC=x,
CD=AC·cosC=x.
在Rt△ABD中,AB=x,AD=x,
∴BD==x.
∴BC=BD+CD=x+x=+,
解得x=2.即AC=2.
10.= [解析]如图,在△ABC中,过点A作AG⊥BC,垂足为G.在△DEF中,过点F作FH⊥DE,交DE的延长线于点H,
则AG=AB·sinB=5sin40°.
∵∠DEF=140°,
∴∠FEH=40°,
∴FH=EF·sin∠FEH=5sin40°,
∴AG=FH.
又∵BC=DE,
∴S△ABC=S△DEF.
11.解:(1)∠B=90°-∠A=90°-60°=30°.
∵cosA=,
∴c====20,
∴a===10.
(2)c===4.
∵tanA===,
∴∠A=30°,
∴∠B=90°-∠A=90°-30°=60°.
12.解:在Rt△ABC中,cosA==,则AB=AC=5,
∴BC==3.
在Rt△BCD中,
∵cos∠DBC=,∠DBC=∠A,
∴=,
∴BD=BC=×3=.
13.解:在Rt△ABC中,∠C=90°,tanA=,
∴∠A=30°,则∠ABC=60°.
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD=30°.
又∵CD=,
∴BC==3.
在Rt△ABC中,∵∠C=90°,∠A=30°,
∴AB==6.
14.[解析](1)过点A作AE⊥BC于点E,根据cosC=,求出∠C=45°,根据AC=,求出AE=CE=1,根据tanB=,求出BE的长;
(2)根据AD是△ABC的中线,求出CD的长,得到DE的长,进而求得sin∠ADC的值.
解:(1)如图,过点A作AE⊥BC于点E.
∵cosC=,
∴∠C=45°.
在Rt△ACE中,CE=AC·cosC=×=1,∴AE=CE=1.
在Rt△ABE中,tanB=,即=,
∴BE=3AE=3,
∴BC=BE+CE=4.
(2)∵AD是△ABC的中线,∴CD=BD=2,
∴DE=CD-CE=1.
∵AE⊥BC,DE=AE=1,∴∠ADC=45°,
∴sin∠ADC=.
15.解:(1)在△ABC中,a2=b2+c2-2bccosA=(2)2+22-2×2×2×=4,则a=2(负值已舍去).
∵22+22=(2)2,即a2+c2=b2,
∴△ABC为直角三角形.
又∵a=c=2,∴∠C=45°.
(2)∵b2=a2+c2-2accosB,a=,b=,cosB=cos45°=,
∴c2-c+1=0,
解得c=.
∵c>a>b,∴c=.
一、选择题
1.[2021·云南] 在△ABC中,∠ABC=90°,若AC=100,sinA=,则AB的长是 ( )
A. B.
C.60 D.80
2.[2020·杭州] 如图1,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则 ( )
图1
A.c=bsinB B.b=csinB
C.a=btanB D.b=ctanB
3.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A的度数为 ( )
A.90° B.60°
C.45° D.30°
4.在直角三角形中,下列条件中不能解直角三角形的是 ( )
A.已知一直角边和一锐角
B.已知斜边和一锐角
C.已知两边
D.已知两角
5.如图2,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是 ( )
图2
A. B.12
C.14 D.21
6.如图3,在△ABC中,∠C=90°,∠A=30°.若BD是△ABC的角平分线,BD=8,则△ABC的三边长分别是 ( )
图3
A.6,6,12 B.2,6,4 C.4,4,8 D.4,12,8
7.如图4,△ABC内接于☉O.若sin∠BAC=,BC=2,则☉O的半径为 ( )
图4
A.3 B.6 C.4 D.2
二、填空题
8.如图5,在Rt△ABC中,∠C=90°,BC=15,tanA=,则AB= .
图5
9.如图6,在△ABC中,BC=+,∠C=45°,AB=AC,则AC的长为 .
图6
10.如图7,在△ABC和△DEF中,∠B=40°,∠E=140°,AB=EF=5,BC=DE=8,则这两个三角形面积的大小关系为S△ABC S△DEF(填“>”“=”或“<”).
图7
三、解答题
11.在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,根据下列条件解直角三角形.
(1)b=10,∠A=60°;
(2)a=2,b=2 .
12.[2020·安徽改编] 如图8,在Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A.若AC=4,cosA=,求BD的长度.
图8
13.[2020·盐城] 如图9,在Rt△ABC中,∠C=90°,tanA=,∠ABC的平分线BD交AC于点D,CD=.求AB的长.
图9
14.如图10,AD是△ABC的中线,tanB=,cosC=,AC=.
求:(1)BC的长;
(2)sin∠ADC的值.
图10
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢 如图11,在锐角三角形ABC中,∠A,∠B,∠ACB所对的边分别为a,b,c(注:sin2A+cos2A=1),过点C作CD⊥AB于点D,在Rt△ADC中,CD=bsinA,AD=bcosA,∴BD=c-bcosA.
在Rt△BDC中,由勾股定理,得CD2+BD2=BC2,
即(bsinA)2+(c-bcosA)2=a2,
整理,得a2=b2+c2-2bccosA.
同理可得b2=a2+c2-2accosB,c2=a2+b2-2abcosC.
(注:上述三个公式对直角三角形和钝角三角形也成立,推理过程同上)
利用上述结论解答下列问题:
(1)在△ABC中,∠A=45°,b=2,c=2,求a的长和∠C的度数;
(2)在△ABC中,a=,b=,∠B=45°,c>a>b,求c的长.
图11
答案
1.D 2.B 3.D 4.D
5.A [解析]如图,过点A作AD⊥BC于点D.
∵在△ABC中,cosB=,
∴∠B=45°,∴BD=AD.
∵sinC==,AC=5,
∴=,
∴AD=3,∴CD=4,BD=3,
则△ABC的面积是·AD·BC=×3×(3+4)=.
6.D [解析]∵∠A=30°,∠C=90°,
∴∠ABC=60°.
∵BD是△ABC的角平分线,
∴∠CBD=30°.
解Rt△BCD,Rt△ABC,即可得△ABC的三边长.
7.A [解析]如图,连接OB,OC,过点O作OD⊥BC于点D,
则∠COD=∠COB=∠BAC,CD=BC=,
∴sin∠COD=sin∠BAC=.又sin∠COD=,
∴=,即=.
∴OC=3.故选A.
8.17 [解析]∵在Rt△ABC中,∠C=90°,tanA==,BC=15,∴=,解得AC=8.根据勾股定理,得AB===17.故答案为17.
9.2 [解析]过点A作AD⊥BC,垂足为D,如图所示.
设AC=x,则AB=x.
在Rt△ACD中,AD=AC·sinC=x,
CD=AC·cosC=x.
在Rt△ABD中,AB=x,AD=x,
∴BD==x.
∴BC=BD+CD=x+x=+,
解得x=2.即AC=2.
10.= [解析]如图,在△ABC中,过点A作AG⊥BC,垂足为G.在△DEF中,过点F作FH⊥DE,交DE的延长线于点H,
则AG=AB·sinB=5sin40°.
∵∠DEF=140°,
∴∠FEH=40°,
∴FH=EF·sin∠FEH=5sin40°,
∴AG=FH.
又∵BC=DE,
∴S△ABC=S△DEF.
11.解:(1)∠B=90°-∠A=90°-60°=30°.
∵cosA=,
∴c====20,
∴a===10.
(2)c===4.
∵tanA===,
∴∠A=30°,
∴∠B=90°-∠A=90°-30°=60°.
12.解:在Rt△ABC中,cosA==,则AB=AC=5,
∴BC==3.
在Rt△BCD中,
∵cos∠DBC=,∠DBC=∠A,
∴=,
∴BD=BC=×3=.
13.解:在Rt△ABC中,∠C=90°,tanA=,
∴∠A=30°,则∠ABC=60°.
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD=30°.
又∵CD=,
∴BC==3.
在Rt△ABC中,∵∠C=90°,∠A=30°,
∴AB==6.
14.[解析](1)过点A作AE⊥BC于点E,根据cosC=,求出∠C=45°,根据AC=,求出AE=CE=1,根据tanB=,求出BE的长;
(2)根据AD是△ABC的中线,求出CD的长,得到DE的长,进而求得sin∠ADC的值.
解:(1)如图,过点A作AE⊥BC于点E.
∵cosC=,
∴∠C=45°.
在Rt△ACE中,CE=AC·cosC=×=1,∴AE=CE=1.
在Rt△ABE中,tanB=,即=,
∴BE=3AE=3,
∴BC=BE+CE=4.
(2)∵AD是△ABC的中线,∴CD=BD=2,
∴DE=CD-CE=1.
∵AE⊥BC,DE=AE=1,∴∠ADC=45°,
∴sin∠ADC=.
15.解:(1)在△ABC中,a2=b2+c2-2bccosA=(2)2+22-2×2×2×=4,则a=2(负值已舍去).
∵22+22=(2)2,即a2+c2=b2,
∴△ABC为直角三角形.
又∵a=c=2,∴∠C=45°.
(2)∵b2=a2+c2-2accosB,a=,b=,cosB=cos45°=,
∴c2-c+1=0,
解得c=.
∵c>a>b,∴c=.
