2021—2022学年人教版九年级数学下册29.2三视图(第3课时)同步练习(word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册29.2三视图(第3课时)同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 16:22:42 | ||
图片预览

文档简介
29.2三视图
第3课时 由三视图到展开图
一、选择题
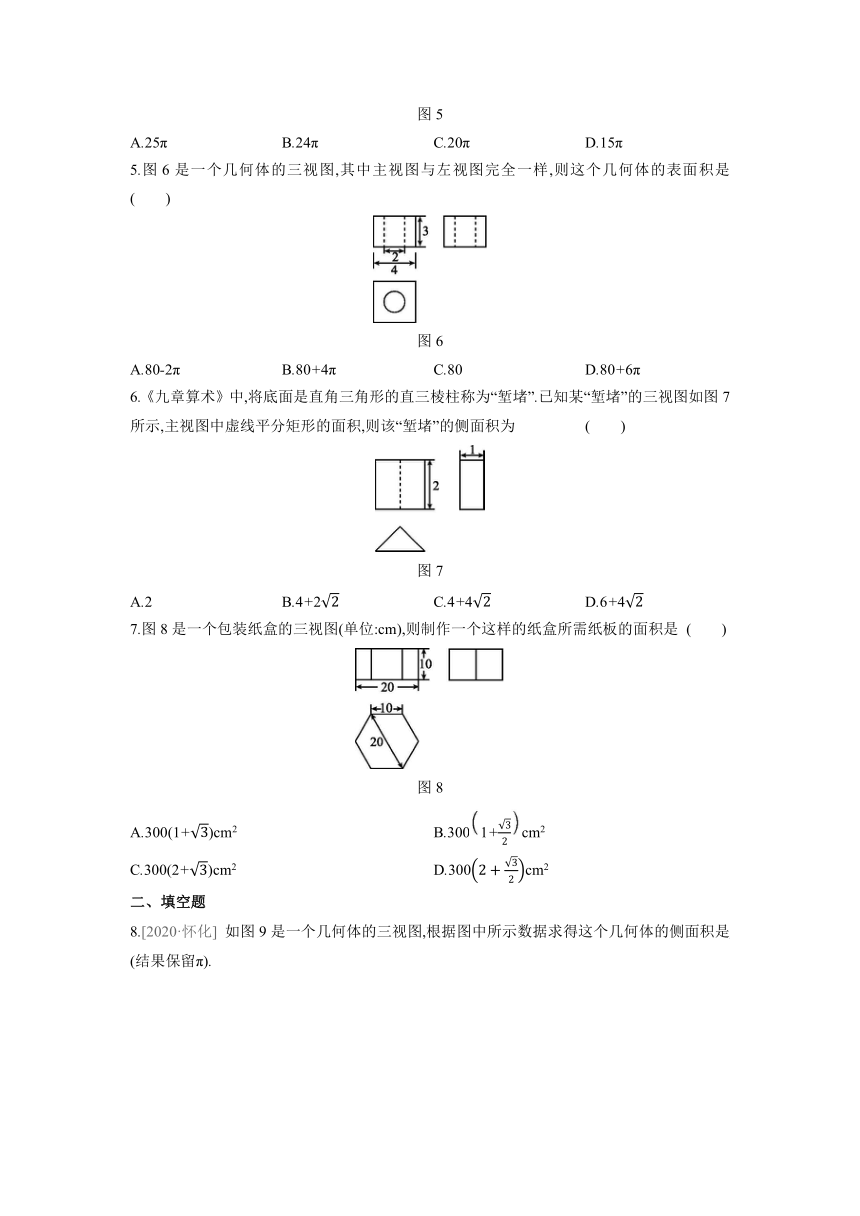
1.图1是一个几何体的展开图,不能作为该几何体的三视图之一的是 ( )
图1
图2
2.某几何体的三视图如图3所示,则下列说法错误的是 ( )
图3
A.该几何体是长方体 B.该几何体的高是3
C.该几何体底面有一边的长是1 D.该几何体的表面积为18
3.[2020·济宁] 如图4是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是 ( )
图4
A.12π cm2 B.15π cm2 C.24π cm2 D.30π cm2
4.图5是某圆锥的主视图和左视图,则该圆锥的侧面积是 ( )
图5
A.25π B.24π C.20π D.15π
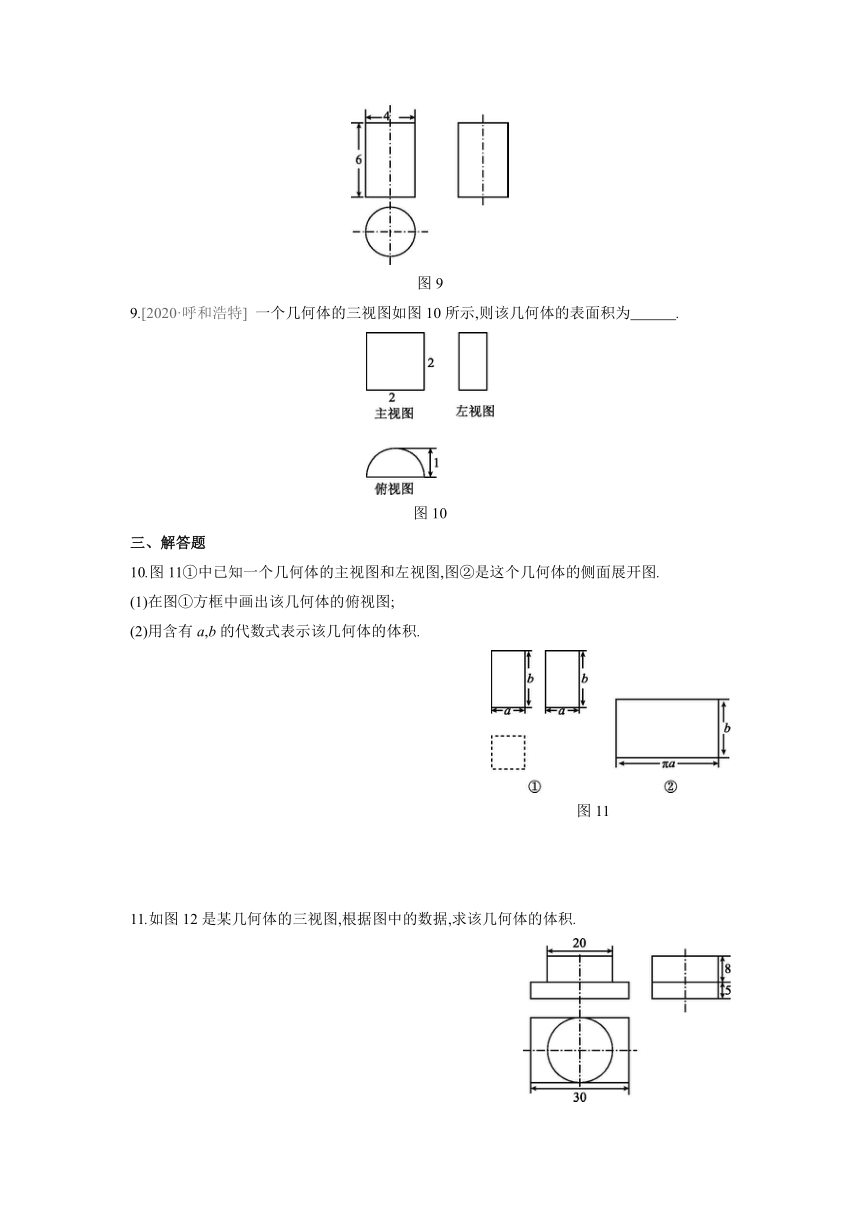
5.图6是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是 ( )
图6
A.80-2π B.80+4π C.80 D.80+6π
6.《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.已知某“堑堵”的三视图如图7所示,主视图中虚线平分矩形的面积,则该“堑堵”的侧面积为 ( )
图7
A.2 B.4+2 C.4+4 D.6+4
7.图8是一个包装纸盒的三视图(单位:cm),则制作一个这样的纸盒所需纸板的面积是 ( )
图8
A.300(1+)cm2 B.3001+cm2
C.300(2+)cm2 D.300cm2
二、填空题
8.[2020·怀化] 如图9是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是 (结果保留π).
图9
9.[2020·呼和浩特] 一个几何体的三视图如图10所示,则该几何体的表面积为 .
图10
三、解答题
10.图11①中已知一个几何体的主视图和左视图,图②是这个几何体的侧面展开图.
(1)在图①方框中画出该几何体的俯视图;
(2)用含有a,b的代数式表示该几何体的体积.
图11
11.如图12是某几何体的三视图,根据图中的数据,求该几何体的体积.
图12
12.[2020·杭州一模] 一个直四棱柱的三视图如图13所示,俯视图是一个菱形,求这个直四棱柱的表面积.
图13
13.图14是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所标数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体的点B出发,沿表面爬到AC的中点D处,请求出蚂蚁爬行的最短路程.
图14
答案
1.D
2.D [解析]该几何体的表面积为2×(1×2+2×3+1×3)=22.故选D.
3.B [解析]由三视图可知这个几何体是圆锥.
∵圆锥底面圆的直径是6cm,
∴圆锥底面圆的半径为3cm.
又∵圆锥的高为4cm,
∴圆锥的母线长为=5(cm),
∴圆锥的侧面积为πrl=π×3×5=15π(cm2).
4.C [解析]根据圆锥的主视图和左视图可知,该圆锥的轴截面是一个底边长为8,高为3的等腰三角形(如图),
AB==5,底面圆半径为4,底面圆周长=8π,∴侧面积为×8π×5=20π.故选C.
5.B [解析]由三视图可知,该几何体是长方体,中间是空心圆柱体,长方体的长、宽、高分别为4,4,3,圆柱体的底面圆直径为2,高为3,长方体的表面积为4×4×2+4×3×4=80,圆柱体的侧面积为2π×3=6π,上、下表面空心圆的面积和为2π,
∴这个几何体的表面积是80+6π-2π=80+4π.
6.C [解析]如图所示,在俯视图中过点C作CD⊥AB,垂足为D,则
由左视图可知CD=1.
∵主视图中虚线平分矩形的面积,∴AD=BD,∴AC=BC,即△ABC是等腰直角三角形.
又∵CD=1,∴AD=BD=CD=1,AC=BC=,
∴该“堑堵”的侧面积为2×(2+2)=4+4.
7.C [解析]包装纸盒的侧面展开图是一个长方形,长方形的长为(10×6)cm,宽为10cm,面积为60×10=600(cm2),包装纸盒的底面是一个正六边形,面积为6××10×10×=150(cm2),故包装纸盒的表面积为600+2×150=600+300=300(2+)cm2.
故选C.
8.24π [解析]由三视图可知该几何体是圆柱体,其底面半径是4÷2=2,高是6,圆柱的侧面展开图是一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,且底面周长为2π×2=4π,∴这个圆柱的侧面积是4π×6=24π.
9.3π+4 [解析]由三视图可知该几何体为半个圆柱,
半个圆柱的底面直径为2,高为2,
故其表面积为π×12+(π+2)×2=3π+4.
故答案为3π+4.
10.解:(1)该几何体的俯视图如图所示.
(2)该几何体的体积为π×a2·b=πa2b.
11.解:由三视图可知,该几何体是由一个圆柱和一个长方体组成的.
圆柱底面圆的直径为20,高为8,长方体的长为30,宽为20,高为5,
故该几何体的体积为π×2×8+30×20×5=800π+3000.
12.解:∵俯视图是菱形,
∴底面菱形的边长为=2.5(cm),面积为×3×4=6(cm2),
则该直四棱柱的侧面积为2.5×8×4=80(cm2),
∴这个直四棱柱的表面积为2×6+80=92(cm2).
13.解:(1)圆锥.
(2)由三视图知该圆锥的底面圆直径为4cm,母线长为6cm,
∴圆锥的侧面积为×4π×6=12π(cm2),底面圆的面积为π×2=4π(cm2),故该几何体的表面积为12π+4π=16π(cm2).
(3)由圆锥母线长为6cm,底面圆半径为2cm,可得此圆锥侧面展开图(扇形)的圆心角为120°,半径为6cm,如图,连接AB',B'C,B'D,则∠B'AC=60°,
∴△AB'C为等边三角形,B'D的长为蚂蚁所爬行的最短路程.
∵D为AC的中点,∴B'D⊥AC,
∴B'D===3(cm),
即蚂蚁爬行的最短路程为3cm.
第3课时 由三视图到展开图
一、选择题
1.图1是一个几何体的展开图,不能作为该几何体的三视图之一的是 ( )
图1
图2
2.某几何体的三视图如图3所示,则下列说法错误的是 ( )
图3
A.该几何体是长方体 B.该几何体的高是3
C.该几何体底面有一边的长是1 D.该几何体的表面积为18
3.[2020·济宁] 如图4是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是 ( )
图4
A.12π cm2 B.15π cm2 C.24π cm2 D.30π cm2
4.图5是某圆锥的主视图和左视图,则该圆锥的侧面积是 ( )
图5
A.25π B.24π C.20π D.15π
5.图6是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是 ( )
图6
A.80-2π B.80+4π C.80 D.80+6π
6.《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.已知某“堑堵”的三视图如图7所示,主视图中虚线平分矩形的面积,则该“堑堵”的侧面积为 ( )
图7
A.2 B.4+2 C.4+4 D.6+4
7.图8是一个包装纸盒的三视图(单位:cm),则制作一个这样的纸盒所需纸板的面积是 ( )
图8
A.300(1+)cm2 B.3001+cm2
C.300(2+)cm2 D.300cm2
二、填空题
8.[2020·怀化] 如图9是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是 (结果保留π).
图9
9.[2020·呼和浩特] 一个几何体的三视图如图10所示,则该几何体的表面积为 .
图10
三、解答题
10.图11①中已知一个几何体的主视图和左视图,图②是这个几何体的侧面展开图.
(1)在图①方框中画出该几何体的俯视图;
(2)用含有a,b的代数式表示该几何体的体积.
图11
11.如图12是某几何体的三视图,根据图中的数据,求该几何体的体积.
图12
12.[2020·杭州一模] 一个直四棱柱的三视图如图13所示,俯视图是一个菱形,求这个直四棱柱的表面积.
图13
13.图14是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所标数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体的点B出发,沿表面爬到AC的中点D处,请求出蚂蚁爬行的最短路程.
图14
答案
1.D
2.D [解析]该几何体的表面积为2×(1×2+2×3+1×3)=22.故选D.
3.B [解析]由三视图可知这个几何体是圆锥.
∵圆锥底面圆的直径是6cm,
∴圆锥底面圆的半径为3cm.
又∵圆锥的高为4cm,
∴圆锥的母线长为=5(cm),
∴圆锥的侧面积为πrl=π×3×5=15π(cm2).
4.C [解析]根据圆锥的主视图和左视图可知,该圆锥的轴截面是一个底边长为8,高为3的等腰三角形(如图),
AB==5,底面圆半径为4,底面圆周长=8π,∴侧面积为×8π×5=20π.故选C.
5.B [解析]由三视图可知,该几何体是长方体,中间是空心圆柱体,长方体的长、宽、高分别为4,4,3,圆柱体的底面圆直径为2,高为3,长方体的表面积为4×4×2+4×3×4=80,圆柱体的侧面积为2π×3=6π,上、下表面空心圆的面积和为2π,
∴这个几何体的表面积是80+6π-2π=80+4π.
6.C [解析]如图所示,在俯视图中过点C作CD⊥AB,垂足为D,则
由左视图可知CD=1.
∵主视图中虚线平分矩形的面积,∴AD=BD,∴AC=BC,即△ABC是等腰直角三角形.
又∵CD=1,∴AD=BD=CD=1,AC=BC=,
∴该“堑堵”的侧面积为2×(2+2)=4+4.
7.C [解析]包装纸盒的侧面展开图是一个长方形,长方形的长为(10×6)cm,宽为10cm,面积为60×10=600(cm2),包装纸盒的底面是一个正六边形,面积为6××10×10×=150(cm2),故包装纸盒的表面积为600+2×150=600+300=300(2+)cm2.
故选C.
8.24π [解析]由三视图可知该几何体是圆柱体,其底面半径是4÷2=2,高是6,圆柱的侧面展开图是一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,且底面周长为2π×2=4π,∴这个圆柱的侧面积是4π×6=24π.
9.3π+4 [解析]由三视图可知该几何体为半个圆柱,
半个圆柱的底面直径为2,高为2,
故其表面积为π×12+(π+2)×2=3π+4.
故答案为3π+4.
10.解:(1)该几何体的俯视图如图所示.
(2)该几何体的体积为π×a2·b=πa2b.
11.解:由三视图可知,该几何体是由一个圆柱和一个长方体组成的.
圆柱底面圆的直径为20,高为8,长方体的长为30,宽为20,高为5,
故该几何体的体积为π×2×8+30×20×5=800π+3000.
12.解:∵俯视图是菱形,
∴底面菱形的边长为=2.5(cm),面积为×3×4=6(cm2),
则该直四棱柱的侧面积为2.5×8×4=80(cm2),
∴这个直四棱柱的表面积为2×6+80=92(cm2).
13.解:(1)圆锥.
(2)由三视图知该圆锥的底面圆直径为4cm,母线长为6cm,
∴圆锥的侧面积为×4π×6=12π(cm2),底面圆的面积为π×2=4π(cm2),故该几何体的表面积为12π+4π=16π(cm2).
(3)由圆锥母线长为6cm,底面圆半径为2cm,可得此圆锥侧面展开图(扇形)的圆心角为120°,半径为6cm,如图,连接AB',B'C,B'D,则∠B'AC=60°,
∴△AB'C为等边三角形,B'D的长为蚂蚁所爬行的最短路程.
∵D为AC的中点,∴B'D⊥AC,
∴B'D===3(cm),
即蚂蚁爬行的最短路程为3cm.
