2021-2022学年沪科版八年级数学上册第14章 全等三角形 单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版八年级数学上册第14章 全等三角形 单元测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 213.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 16:41:31 | ||
图片预览

文档简介
第14章全等三角形单元测试卷 2021-2022学年沪科版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,ABCCDA,AC=7 cm,AB=5 cm,BC=8 cm,则CD的长是( )
A. B.
C. D.
如图所示,AB=CD,AC=BD,则下列说法正确的是( )
A. 可用“”直接证明
B. 可用“”直接证明
C. 可用“”直接证明
D. 可用“”直接证明
要测量池塘的宽度AB,画出如图所示的两个三角形,下面所测出的条件中不能得出CD=AB的是( )
A. ,
B. ,
C. ,
D. ,
根据下列条件,能唯一画出ABC的是( )
A. ,,
B. ,,
C. ,,
D. ,
如图,在PAB中,A=B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若MKN=,则P的度数为( )
A. B.
C. D.
如图,已知AB,CD相交于点O,AOCBOD,E,F分别在OA,OB上,要使EOCFOD,添加的一个条件不可以是( )
A.
B.
C.
D.
如图,点A在DE上,AC=CE,1=2=3,则DE的长等于( )
A. B.
C. D.
如图,AD,BE是锐角ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为( )
A. B.
C. D.
如图是55的正方形网格,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与ABC全等,这样的格点三角形最多可以画出( )
A. 个 B. 个
C. 个 D. 个
如图,已知AC与BD相交于点O,ADBC,且AD=BC,过O点作任意一条直线与AD,BC交于点E,F,则下列结论:OA=OC;OE=OF;AE=CF;OB=OD.其中成立的有( )
A. 个 B. 个
C. 个 D. 个
二、填空题(本大题共4小题,共12分)
如图,ABCEDF,AE=20 cm,FC=10 cm,则AC的长为 cm.
如图,在ABC中,C=BED=,AC=AE,且CDA=,则BDE= .
如图,已知ABBD,垂足为B,EDBD,垂足为D,AB=CD,AC=CE.若连接AE,则ACE是 三角形.(填“锐角”“直角”或“钝角”)
如图,AB=AC,CD和BE相交于点O,连接BC.
(1)要使ABEACD,应添加的条件是 (添加一个条件即可).
(2)在(1)的条件下,图中全等的三角形(不包括ABEACD)还有 对.
三、解答题(本大题共9小题,共78分)
如图,C是线段AB的中点,CD=BE,CDBE.求证:D=E.
如图,已知A,F,C,D在同一直线上,BC=EF,AB=DE,AF=CD.求证:BCEF.
如图,AD是ABC的高,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD.求证:BEAC.
下面四个条件中,请以其中两个为已知条件,第三个为结论,推出一个真命题(只需写出一种情况)并证明.条件:AE=AD;AB=AC;OB=OC;B=C.
已知: .
求证: .
证明:
如图,在ABC中,ACB=,AC=BC,BECE于点E,ADCE于点D.求证:BECCDA.
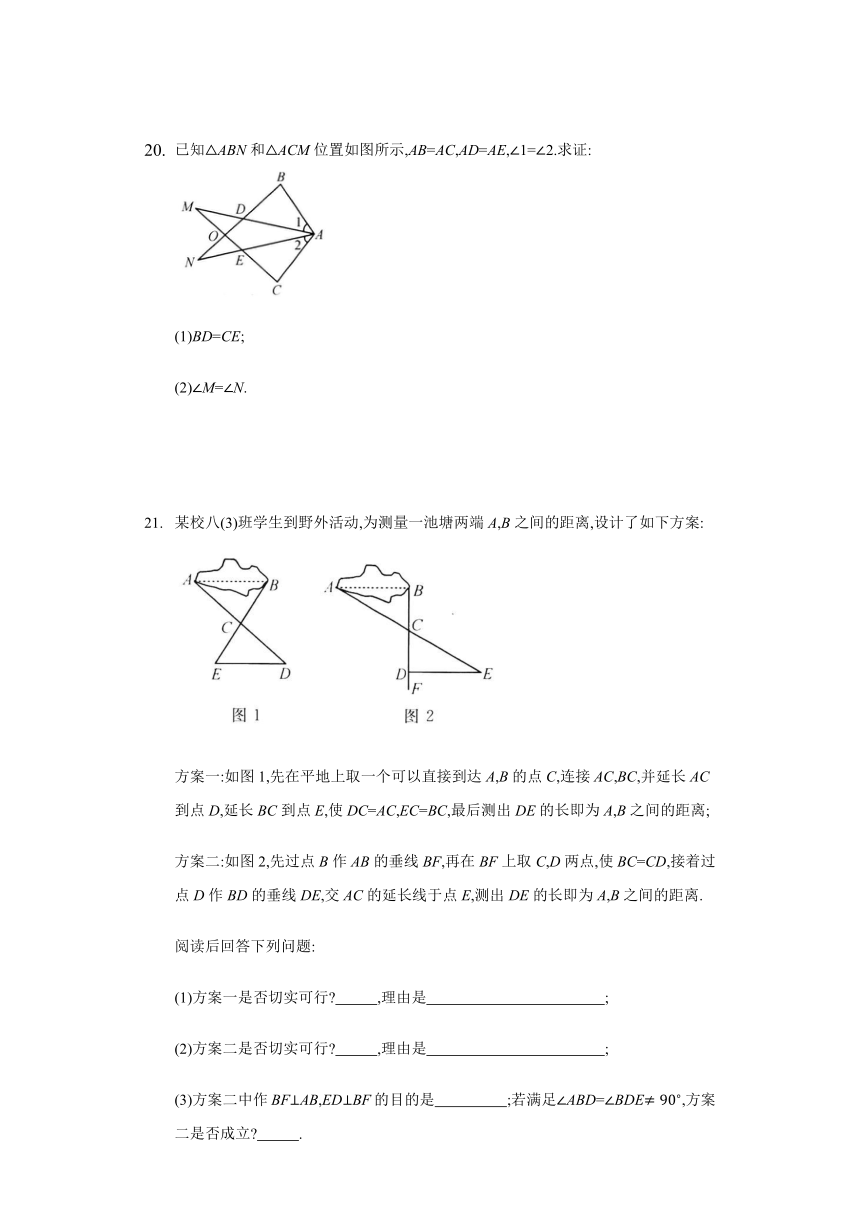
已知ABN和ACM位置如图所示,AB=AC,AD=AE,1=2.求证:
(1)BD=CE;
(2)M=N.
某校八(3)班学生到野外活动,为测量一池塘两端A,B之间的距离,设计了如下方案:
方案一:如图1,先在平地上取一个可以直接到达A,B的点C,连接AC,BC,并延长AC到点D,延长BC到点E,使DC=AC,EC=BC,最后测出DE的长即为A,B之间的距离;
方案二:如图2,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,测出DE的长即为A,B之间的距离.
阅读后回答下列问题:
(1)方案一是否切实可行 ,理由是 ;
(2)方案二是否切实可行 ,理由是 ;
(3)方案二中作BFAB,EDBF的目的是 ;若满足ABD=BDE,方案二是否成立 .
如图所示,ABCADE,BC的延长线交AD于点F,交DE于点G.若CAD=,B=D=,EAB=,求AED,BFD以及DGB的度数.
(1)如图1,MAN=,射线AE在这个角的内部,点B,C分别在MAN的边AM,AN上,且AB=AC,CFAE于点F,BDAE于点D.求证:ABDCAF;
(2)如图2,点B,C分别在MAN的边AM,AN上,点E,F都在MAN内部的射线AD上,1,2分别是ABE,CAF的外角.已知AB=AC,且1=2=BAC.求证:ABECAF;
(3)如图3,在ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E,F在线段AD上,1=2=BAC.若ABC的面积为15,求ACF与BDE的面积之和.
参考答案
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】15
12.【答案】
13.【答案】直角
14.【答案】AD=AE(答案不唯一) 2
15.【答案】证明:C是线段AB的中点,
AC=CB.
CDBE,
ACD=B.
在ACD和CBE中,
ACDCBE(SAS).
D=E.
16.【答案】证明:AF=CD,
AF+CF=CD+CF,即AC=DF.
在ABC和DEF中,
ABCDEF(SSS).
BCA=EFD.
BCEF.
17.【答案】证明:ADBC,
ADC=BDF=.
在RtADC和RtBDF中,
RtADCRtBDF(HL).
CAD=FBD.
AEB=C+FBD=C+CAD=.
BEAC.
18.【答案】解:
证明:在ACD和ABE中,
ACDABE(SAS).
B=C.(答案不唯一)
19.【答案】证明:BECE于点E,ADCE于点D,
BEC=CDA=.
在RtBEC中,BCE+CBE=,
在RtBCA中,BCE+ACD=,
CBE=ACD.
在BEC和CDA中,
BECCDA(AAS).
20.【答案】证明:(1)在ABD和ACE中,
ABDACE(SAS).
BD=CE.
(2)1=2,
1+DAE=2+DAE,即BAN=CAM.
由(1)ABDACE,
B=C.
在ACM和ABN中,
ACMABN(ASA).
M=N.
21.【答案】解:(1)可行,满足边角边判定法,可判定ABCDEC,因而AB=DE;
(2)可行,满足角边角判定法,可判定ABCEDC,因而AB=DE;
(3)使ABC=EDC,成立.
22.【答案】解:ABCADE,
BAC=DAE,
EAB=120°,
DAE+CAD+BAC=120°,
CAD=20°,
BAC=DAE=(120°-20°)=,
AED=180°-50°-35°=95°,
BAF=BAC+CAD=70°,
BFD=BAF+B=+=;
BFD=D+DGB,
DGB=-=,
即AED、BFD和DGB的度数分别为、、.
23.【答案】解:(1)证明:CFAE,BDAE,MAN=,
BDA=AFC=.
ABD+BAD=,BAD+CAF=.
ABD=CAF.
在ABD和CAF中,
ABDCAF(AAS).
(2)证明:1=2=BAC,1=BAE+ABE,BAC=BAE+CAF,2=FCA+CAF,
ABE=CAF,BAE=FCA.
在ABE和CAF中,
ABECAF(ASA).
(3)ABC的面积为15,CD=2BD,
ABD的面积为15=5.
ABECAF,
ACF与BDE的面积之和等于ABE与BDE的面积之和,即等于ABD的面积5.第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
如图,ABCCDA,AC=7 cm,AB=5 cm,BC=8 cm,则CD的长是( )
A. B.
C. D.
如图所示,AB=CD,AC=BD,则下列说法正确的是( )
A. 可用“”直接证明
B. 可用“”直接证明
C. 可用“”直接证明
D. 可用“”直接证明
要测量池塘的宽度AB,画出如图所示的两个三角形,下面所测出的条件中不能得出CD=AB的是( )
A. ,
B. ,
C. ,
D. ,
根据下列条件,能唯一画出ABC的是( )
A. ,,
B. ,,
C. ,,
D. ,
如图,在PAB中,A=B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若MKN=,则P的度数为( )
A. B.
C. D.
如图,已知AB,CD相交于点O,AOCBOD,E,F分别在OA,OB上,要使EOCFOD,添加的一个条件不可以是( )
A.
B.
C.
D.
如图,点A在DE上,AC=CE,1=2=3,则DE的长等于( )
A. B.
C. D.
如图,AD,BE是锐角ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为( )
A. B.
C. D.
如图是55的正方形网格,以点D,E为两个顶点作位置不同的格点三角形,使所作的格点三角形与ABC全等,这样的格点三角形最多可以画出( )
A. 个 B. 个
C. 个 D. 个
如图,已知AC与BD相交于点O,ADBC,且AD=BC,过O点作任意一条直线与AD,BC交于点E,F,则下列结论:OA=OC;OE=OF;AE=CF;OB=OD.其中成立的有( )
A. 个 B. 个
C. 个 D. 个
二、填空题(本大题共4小题,共12分)
如图,ABCEDF,AE=20 cm,FC=10 cm,则AC的长为 cm.
如图,在ABC中,C=BED=,AC=AE,且CDA=,则BDE= .
如图,已知ABBD,垂足为B,EDBD,垂足为D,AB=CD,AC=CE.若连接AE,则ACE是 三角形.(填“锐角”“直角”或“钝角”)
如图,AB=AC,CD和BE相交于点O,连接BC.
(1)要使ABEACD,应添加的条件是 (添加一个条件即可).
(2)在(1)的条件下,图中全等的三角形(不包括ABEACD)还有 对.
三、解答题(本大题共9小题,共78分)
如图,C是线段AB的中点,CD=BE,CDBE.求证:D=E.
如图,已知A,F,C,D在同一直线上,BC=EF,AB=DE,AF=CD.求证:BCEF.
如图,AD是ABC的高,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD.求证:BEAC.
下面四个条件中,请以其中两个为已知条件,第三个为结论,推出一个真命题(只需写出一种情况)并证明.条件:AE=AD;AB=AC;OB=OC;B=C.
已知: .
求证: .
证明:
如图,在ABC中,ACB=,AC=BC,BECE于点E,ADCE于点D.求证:BECCDA.
已知ABN和ACM位置如图所示,AB=AC,AD=AE,1=2.求证:
(1)BD=CE;
(2)M=N.
某校八(3)班学生到野外活动,为测量一池塘两端A,B之间的距离,设计了如下方案:
方案一:如图1,先在平地上取一个可以直接到达A,B的点C,连接AC,BC,并延长AC到点D,延长BC到点E,使DC=AC,EC=BC,最后测出DE的长即为A,B之间的距离;
方案二:如图2,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,测出DE的长即为A,B之间的距离.
阅读后回答下列问题:
(1)方案一是否切实可行 ,理由是 ;
(2)方案二是否切实可行 ,理由是 ;
(3)方案二中作BFAB,EDBF的目的是 ;若满足ABD=BDE,方案二是否成立 .
如图所示,ABCADE,BC的延长线交AD于点F,交DE于点G.若CAD=,B=D=,EAB=,求AED,BFD以及DGB的度数.
(1)如图1,MAN=,射线AE在这个角的内部,点B,C分别在MAN的边AM,AN上,且AB=AC,CFAE于点F,BDAE于点D.求证:ABDCAF;
(2)如图2,点B,C分别在MAN的边AM,AN上,点E,F都在MAN内部的射线AD上,1,2分别是ABE,CAF的外角.已知AB=AC,且1=2=BAC.求证:ABECAF;
(3)如图3,在ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E,F在线段AD上,1=2=BAC.若ABC的面积为15,求ACF与BDE的面积之和.
参考答案
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】15
12.【答案】
13.【答案】直角
14.【答案】AD=AE(答案不唯一) 2
15.【答案】证明:C是线段AB的中点,
AC=CB.
CDBE,
ACD=B.
在ACD和CBE中,
ACDCBE(SAS).
D=E.
16.【答案】证明:AF=CD,
AF+CF=CD+CF,即AC=DF.
在ABC和DEF中,
ABCDEF(SSS).
BCA=EFD.
BCEF.
17.【答案】证明:ADBC,
ADC=BDF=.
在RtADC和RtBDF中,
RtADCRtBDF(HL).
CAD=FBD.
AEB=C+FBD=C+CAD=.
BEAC.
18.【答案】解:
证明:在ACD和ABE中,
ACDABE(SAS).
B=C.(答案不唯一)
19.【答案】证明:BECE于点E,ADCE于点D,
BEC=CDA=.
在RtBEC中,BCE+CBE=,
在RtBCA中,BCE+ACD=,
CBE=ACD.
在BEC和CDA中,
BECCDA(AAS).
20.【答案】证明:(1)在ABD和ACE中,
ABDACE(SAS).
BD=CE.
(2)1=2,
1+DAE=2+DAE,即BAN=CAM.
由(1)ABDACE,
B=C.
在ACM和ABN中,
ACMABN(ASA).
M=N.
21.【答案】解:(1)可行,满足边角边判定法,可判定ABCDEC,因而AB=DE;
(2)可行,满足角边角判定法,可判定ABCEDC,因而AB=DE;
(3)使ABC=EDC,成立.
22.【答案】解:ABCADE,
BAC=DAE,
EAB=120°,
DAE+CAD+BAC=120°,
CAD=20°,
BAC=DAE=(120°-20°)=,
AED=180°-50°-35°=95°,
BAF=BAC+CAD=70°,
BFD=BAF+B=+=;
BFD=D+DGB,
DGB=-=,
即AED、BFD和DGB的度数分别为、、.
23.【答案】解:(1)证明:CFAE,BDAE,MAN=,
BDA=AFC=.
ABD+BAD=,BAD+CAF=.
ABD=CAF.
在ABD和CAF中,
ABDCAF(AAS).
(2)证明:1=2=BAC,1=BAE+ABE,BAC=BAE+CAF,2=FCA+CAF,
ABE=CAF,BAE=FCA.
在ABE和CAF中,
ABECAF(ASA).
(3)ABC的面积为15,CD=2BD,
ABD的面积为15=5.
ABECAF,
ACF与BDE的面积之和等于ABE与BDE的面积之和,即等于ABD的面积5.第2页,共2页
