2021—2022学年人教版九年级数学下册第二十九章 投影与视图单元测试题(word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册第二十九章 投影与视图单元测试题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 280.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 00:00:00 | ||
图片预览


文档简介
第二十九章 投影与视图
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列物体的光线所形成的投影是平行投影的是 ( )
A.台灯 B.手电筒
C.太阳 D.路灯
2.正方形的正投影不可能是 ( )
A.线段 B.矩形
C.正方形 D.梯形
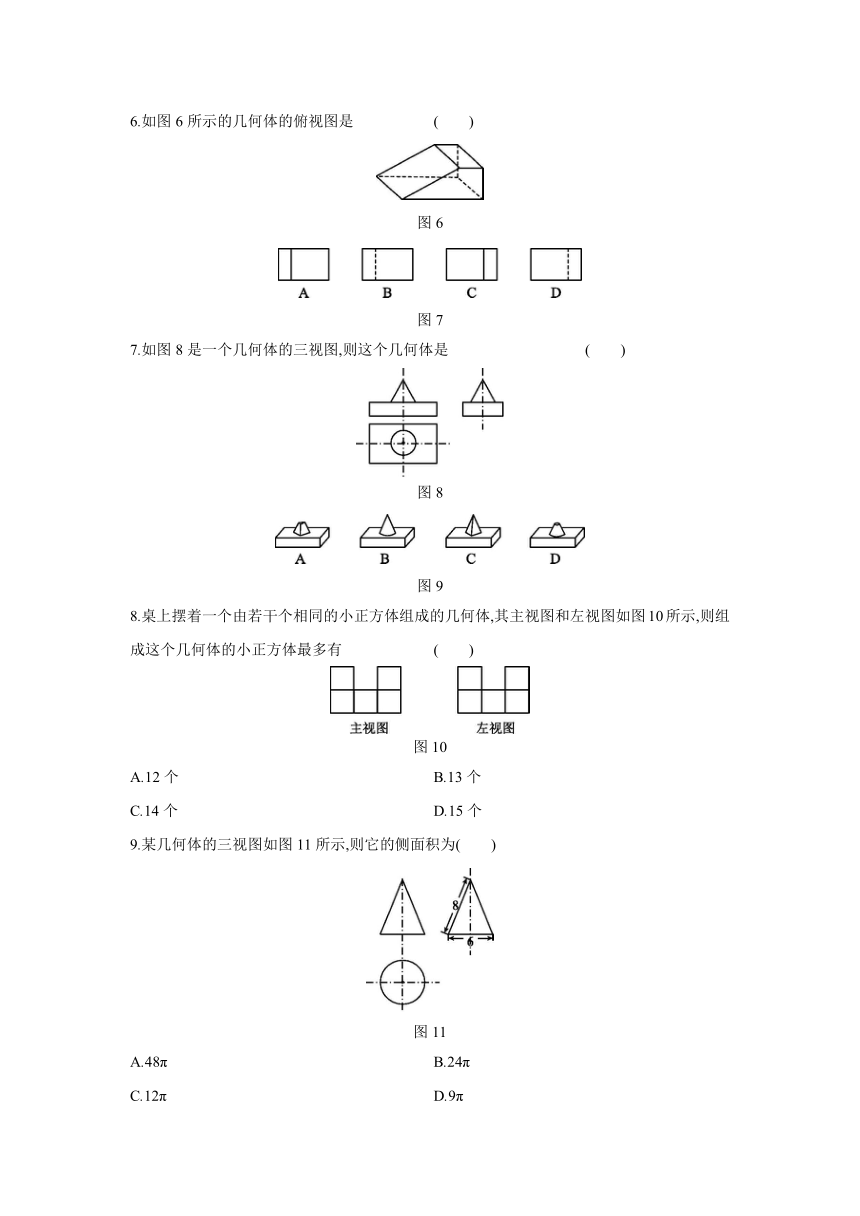
3.四个相同的小正方体组成的立体图形如图1所示,它的主视图为 ( )
图1
图2
4.五个大小相同的小正方体搭成的几何体如图3所示,其左视图是 ( )
图3
图4
5.下列立体图形中,俯视图不是圆的是 ( )
图5
6.如图6所示的几何体的俯视图是 ( )
图6
图7
7.如图8是一个几何体的三视图,则这个几何体是 ( )
图8
图9
8.桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图10所示,则组成这个几何体的小正方体最多有 ( )
图10
A.12个 B.13个
C.14个 D.15个
9.某几何体的三视图如图11所示,则它的侧面积为( )
图11
A.48π B.24π
C.12π D.9π
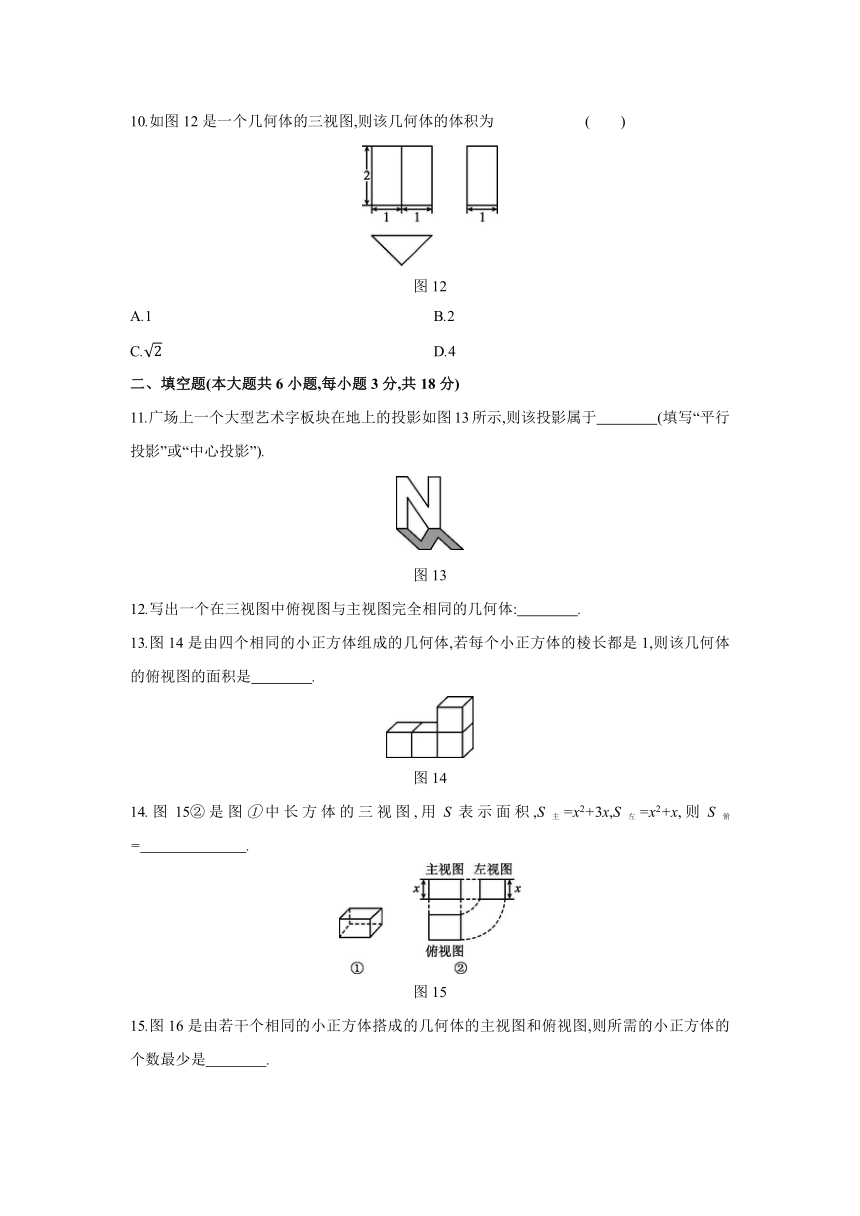
10.如图12是一个几何体的三视图,则该几何体的体积为 ( )
图12
A.1 B.2
C. D.4
二、填空题(本大题共6小题,每小题3分,共18分)
11.广场上一个大型艺术字板块在地上的投影如图13所示,则该投影属于 (填写“平行投影”或“中心投影”).
图13
12.写出一个在三视图中俯视图与主视图完全相同的几何体: .
13.图14是由四个相同的小正方体组成的几何体,若每个小正方体的棱长都是1,则该几何体的俯视图的面积是 .
图14
14.图15②是图①中长方体的三视图,用S表示面积,S主=x2+3x,S左=x2+x,则S俯= .
图15
15.图16是由若干个相同的小正方体搭成的几何体的主视图和俯视图,则所需的小正方体的个数最少是 .
图16
16.如图17,小超想要测量窗外的路灯PH的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点C的影子落在地板上的B处、窗户的最低点D的影子落在地板上的A处,小超测得窗户距地面的高度QD=1 m,窗高CD=1.5 m,并测得AQ=1 m,AB=2 m(点P,Q,A,B在同一直线上,点C,D,Q在同一直线上).则窗外的路灯PH的高度为 .
图17
三、解答题(本大题共7小题,共52分)
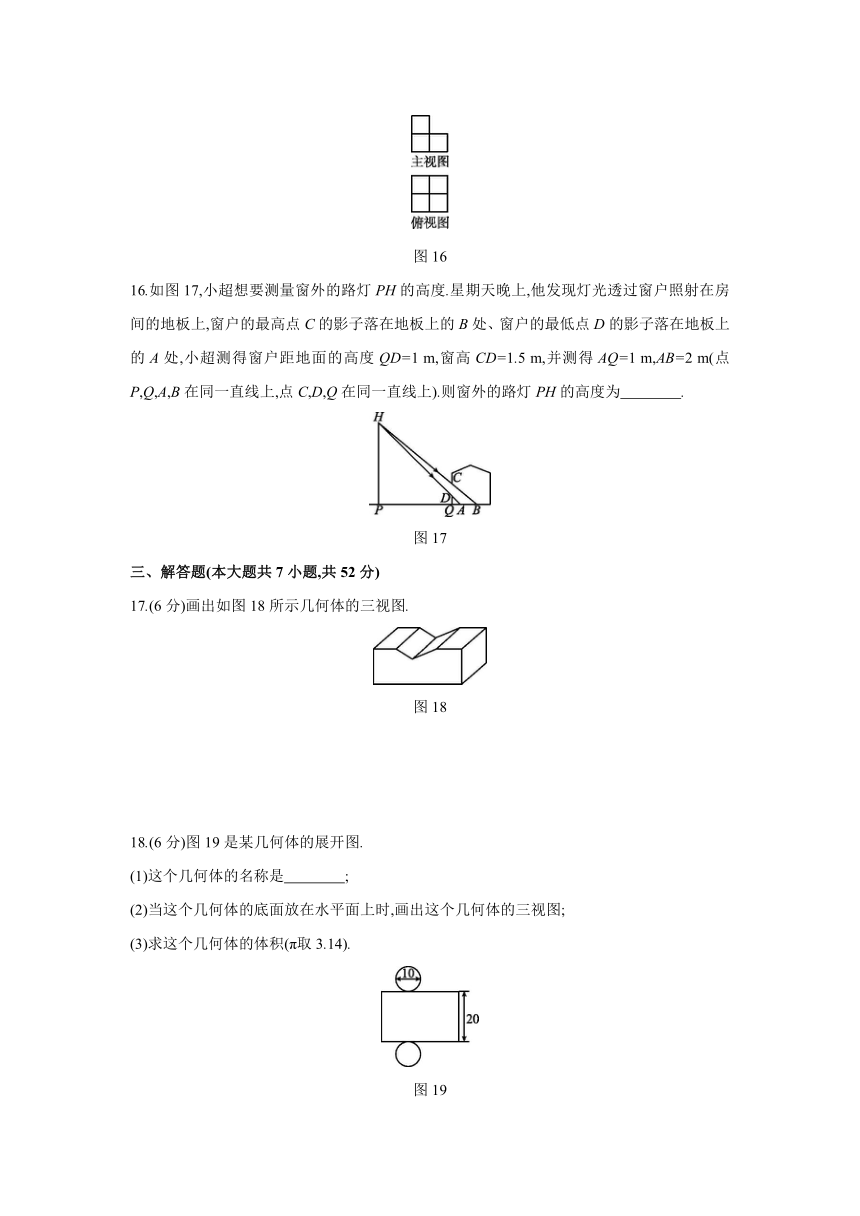
17.(6分)画出如图18所示几何体的三视图.
图18
18.(6分)图19是某几何体的展开图.
(1)这个几何体的名称是 ;
(2)当这个几何体的底面放在水平面上时,画出这个几何体的三视图;
(3)求这个几何体的体积(π取3.14).
图19
19.(7分)如图20,AB和DE是直立在地面上的两根立柱.AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
图20
20.(8分)如图21,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,留在墙上的影高为2米,求旗杆的高度.
图21
21.(8分)如图22,在同一时刻,身高为1.6 m的小明(AB)在路灯下的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方点H处,并测得HB=6 m.
(1)在图中画出路灯灯泡所在的位置G,并求路灯灯泡的垂直高度GH;
(2)如果小明沿线段BH向小颖(点H)走去,当小明走到BH的中点B1处时,画出小明的影子B1C1,并求出B1C1的长.
图22
22.(8分)如图23,AB是公园的一圆形桌面的主视图,MN表示该桌面在路灯下的影子;CD是一个圆形凳子的主视图.(桌面、凳面均与地面平行)
(1)请你在图中标出路灯O的位置,并画出CD的影子PQ(要求保留画图痕迹,光线用虚线表示);
(2)若桌面直径和桌面与地面的距离均为1.2 m,测得影子的最大跨度MN为2 m,求路灯O与地面的距离.
图23
23.(9分)如图24,一个几何体的三视图是两个矩形、一个扇形,求这个几何体的表面积(结果保留π).
图24
答案
1.C 2.D 3.A 4.C 5.C 6.C 7.B
8.B [解析]底层最多有9个小正方体,第二层最多有4个小正方体,所以组成这个几何体的小正方体最多有13个.
9.B [解析]由几何体的三视图判断出已知几何体为圆锥,再根据已知数据求出圆锥的侧面积.由已知三视图可求出圆锥的底面半径为3,母线长为8,故圆锥的侧面积为π×3×8=24π.
10.B [解析]这是一个直三棱柱,其底面是斜边为2的等腰直角三角形,且棱柱的高是2,因此其体积=×2×1×2=2.故选B.
11.平行投影
12.球(答案不唯一)
13.3 [解析]俯视图是由三个小正方形组成的矩形,矩形的面积为1×3=3.
14.x2+4x+3 [解析]由S主=x2+3x=x(x+3),S左=x2+x=x(1+x),及“长对正,高平齐,宽相等”可知:长方体的长为(x+3),宽为(1+x),高为x.长方体的俯视图是由长和宽组成的矩形,所以S俯=(x+3)(1+x)=x2+4x+3.
15.5
16.10m [解析]连接CD.
∵DQ⊥PB,
∴∠CQB=90°.
∵QD=1m,AQ=1m,
∴∠ADQ=∠QAD=45°.
∵PH⊥PB,
∴∠HPA=90°,
∴∠AHP=45°,
∴PH=PA.
设PH=PA=xm.
∵PH⊥PB,CQ⊥PB,
∴PH∥CQ,
∴△PBH∽△QBC,
∴=,即=,
解得x=10,经检验,x=10是原方程的解,且符合题意.
故窗外的路灯PH的高度为10m.
17.解:几何体的三视图如图所示.
18.[解析](1)两底面为圆,侧面展开图为矩形,很显然是圆柱体;(2)主视图、左视图、俯视图分别为矩形、矩形、圆;(3)底面圆半径为5,高为20,由圆柱体的体积公式即可求解.
解:(1)圆柱
(2)如图所示.
(3)这个几何体的体积为π×52×20=500π≈1570.
19.解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为此时DE在阳光下的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
又∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴AB∶DE=BC∶EF.
∵AB=4m,BC=3m,EF=8m,
∴4∶DE=3∶8,
∴DE=(m).
20.解:过点C作CE⊥AB于点E,如图.
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,
∴四边形CDBE为矩形,
∴CE=BD=21米,BE=CD=2米.
设AE=x米,
则=,
解得x=14,
∴旗杆的高AB=AE+BE=14+2=16(米).
答:旗杆的高度为16米.
21.解:(1)路灯灯泡所在的位置G如图所示.
∵AB∥GH,∴△ABC∽△GHC,
∴=,即=,
解得GH=4.8(m).
即路灯灯泡的垂直高度GH是4.8m.
(2)小明的影子B1C1如图所示.
∵A1B1∥GH,
∴△A1B1C1∽△GHC1,
∴=.
设B1C1的长为xm,则=,
解得x=1.5.
经检验,x=1.5是原方程的解,且符合题意.
即B1C1的长为1.5m.
22.解:(1)如图,连接MA,NB并延长,它们交于点O,连接OC,OD并延长,分别交地面于点P,Q,则PQ为CD的影子.
(2)过点O作OF⊥MN于点F,交AB于点E,如图,则OE⊥AB.
由题意得AB=1.2m,EF=1.2m,MN=2m.
∵AB∥MN,∴△OAB∽△OMN,
∴AB∶MN=OE∶OF,
即1.2∶2=(OF-1.2)∶OF,
解得OF=3(m).
答:路灯O与地面的距离为3m.
23.解:由几何体的三视图可得:
该几何体是一个残缺的圆柱,侧面是由一个曲的面和两个长方形构成的,上、下底面是两个扇形,
该几何体的侧面积为3××2π×2+2+2=9π+12,
上、下底面的面积和为2××π×22=6π,
故这个几何体的表面积为9π+12+6π=15π+12.
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列物体的光线所形成的投影是平行投影的是 ( )
A.台灯 B.手电筒
C.太阳 D.路灯
2.正方形的正投影不可能是 ( )
A.线段 B.矩形
C.正方形 D.梯形
3.四个相同的小正方体组成的立体图形如图1所示,它的主视图为 ( )
图1
图2
4.五个大小相同的小正方体搭成的几何体如图3所示,其左视图是 ( )
图3
图4
5.下列立体图形中,俯视图不是圆的是 ( )
图5
6.如图6所示的几何体的俯视图是 ( )
图6
图7
7.如图8是一个几何体的三视图,则这个几何体是 ( )
图8
图9
8.桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图10所示,则组成这个几何体的小正方体最多有 ( )
图10
A.12个 B.13个
C.14个 D.15个
9.某几何体的三视图如图11所示,则它的侧面积为( )
图11
A.48π B.24π
C.12π D.9π
10.如图12是一个几何体的三视图,则该几何体的体积为 ( )
图12
A.1 B.2
C. D.4
二、填空题(本大题共6小题,每小题3分,共18分)
11.广场上一个大型艺术字板块在地上的投影如图13所示,则该投影属于 (填写“平行投影”或“中心投影”).
图13
12.写出一个在三视图中俯视图与主视图完全相同的几何体: .
13.图14是由四个相同的小正方体组成的几何体,若每个小正方体的棱长都是1,则该几何体的俯视图的面积是 .
图14
14.图15②是图①中长方体的三视图,用S表示面积,S主=x2+3x,S左=x2+x,则S俯= .
图15
15.图16是由若干个相同的小正方体搭成的几何体的主视图和俯视图,则所需的小正方体的个数最少是 .
图16
16.如图17,小超想要测量窗外的路灯PH的高度.星期天晚上,他发现灯光透过窗户照射在房间的地板上,窗户的最高点C的影子落在地板上的B处、窗户的最低点D的影子落在地板上的A处,小超测得窗户距地面的高度QD=1 m,窗高CD=1.5 m,并测得AQ=1 m,AB=2 m(点P,Q,A,B在同一直线上,点C,D,Q在同一直线上).则窗外的路灯PH的高度为 .
图17
三、解答题(本大题共7小题,共52分)
17.(6分)画出如图18所示几何体的三视图.
图18
18.(6分)图19是某几何体的展开图.
(1)这个几何体的名称是 ;
(2)当这个几何体的底面放在水平面上时,画出这个几何体的三视图;
(3)求这个几何体的体积(π取3.14).
图19
19.(7分)如图20,AB和DE是直立在地面上的两根立柱.AB=4 m,某一时刻AB在阳光下的投影BC=3 m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8 m,请你计算DE的长.
图20
20.(8分)如图21,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,留在墙上的影高为2米,求旗杆的高度.
图21
21.(8分)如图22,在同一时刻,身高为1.6 m的小明(AB)在路灯下的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方点H处,并测得HB=6 m.
(1)在图中画出路灯灯泡所在的位置G,并求路灯灯泡的垂直高度GH;
(2)如果小明沿线段BH向小颖(点H)走去,当小明走到BH的中点B1处时,画出小明的影子B1C1,并求出B1C1的长.
图22
22.(8分)如图23,AB是公园的一圆形桌面的主视图,MN表示该桌面在路灯下的影子;CD是一个圆形凳子的主视图.(桌面、凳面均与地面平行)
(1)请你在图中标出路灯O的位置,并画出CD的影子PQ(要求保留画图痕迹,光线用虚线表示);
(2)若桌面直径和桌面与地面的距离均为1.2 m,测得影子的最大跨度MN为2 m,求路灯O与地面的距离.
图23
23.(9分)如图24,一个几何体的三视图是两个矩形、一个扇形,求这个几何体的表面积(结果保留π).
图24
答案
1.C 2.D 3.A 4.C 5.C 6.C 7.B
8.B [解析]底层最多有9个小正方体,第二层最多有4个小正方体,所以组成这个几何体的小正方体最多有13个.
9.B [解析]由几何体的三视图判断出已知几何体为圆锥,再根据已知数据求出圆锥的侧面积.由已知三视图可求出圆锥的底面半径为3,母线长为8,故圆锥的侧面积为π×3×8=24π.
10.B [解析]这是一个直三棱柱,其底面是斜边为2的等腰直角三角形,且棱柱的高是2,因此其体积=×2×1×2=2.故选B.
11.平行投影
12.球(答案不唯一)
13.3 [解析]俯视图是由三个小正方形组成的矩形,矩形的面积为1×3=3.
14.x2+4x+3 [解析]由S主=x2+3x=x(x+3),S左=x2+x=x(1+x),及“长对正,高平齐,宽相等”可知:长方体的长为(x+3),宽为(1+x),高为x.长方体的俯视图是由长和宽组成的矩形,所以S俯=(x+3)(1+x)=x2+4x+3.
15.5
16.10m [解析]连接CD.
∵DQ⊥PB,
∴∠CQB=90°.
∵QD=1m,AQ=1m,
∴∠ADQ=∠QAD=45°.
∵PH⊥PB,
∴∠HPA=90°,
∴∠AHP=45°,
∴PH=PA.
设PH=PA=xm.
∵PH⊥PB,CQ⊥PB,
∴PH∥CQ,
∴△PBH∽△QBC,
∴=,即=,
解得x=10,经检验,x=10是原方程的解,且符合题意.
故窗外的路灯PH的高度为10m.
17.解:几何体的三视图如图所示.
18.[解析](1)两底面为圆,侧面展开图为矩形,很显然是圆柱体;(2)主视图、左视图、俯视图分别为矩形、矩形、圆;(3)底面圆半径为5,高为20,由圆柱体的体积公式即可求解.
解:(1)圆柱
(2)如图所示.
(3)这个几何体的体积为π×52×20=500π≈1570.
19.解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为此时DE在阳光下的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
又∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴AB∶DE=BC∶EF.
∵AB=4m,BC=3m,EF=8m,
∴4∶DE=3∶8,
∴DE=(m).
20.解:过点C作CE⊥AB于点E,如图.
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,
∴四边形CDBE为矩形,
∴CE=BD=21米,BE=CD=2米.
设AE=x米,
则=,
解得x=14,
∴旗杆的高AB=AE+BE=14+2=16(米).
答:旗杆的高度为16米.
21.解:(1)路灯灯泡所在的位置G如图所示.
∵AB∥GH,∴△ABC∽△GHC,
∴=,即=,
解得GH=4.8(m).
即路灯灯泡的垂直高度GH是4.8m.
(2)小明的影子B1C1如图所示.
∵A1B1∥GH,
∴△A1B1C1∽△GHC1,
∴=.
设B1C1的长为xm,则=,
解得x=1.5.
经检验,x=1.5是原方程的解,且符合题意.
即B1C1的长为1.5m.
22.解:(1)如图,连接MA,NB并延长,它们交于点O,连接OC,OD并延长,分别交地面于点P,Q,则PQ为CD的影子.
(2)过点O作OF⊥MN于点F,交AB于点E,如图,则OE⊥AB.
由题意得AB=1.2m,EF=1.2m,MN=2m.
∵AB∥MN,∴△OAB∽△OMN,
∴AB∶MN=OE∶OF,
即1.2∶2=(OF-1.2)∶OF,
解得OF=3(m).
答:路灯O与地面的距离为3m.
23.解:由几何体的三视图可得:
该几何体是一个残缺的圆柱,侧面是由一个曲的面和两个长方形构成的,上、下底面是两个扇形,
该几何体的侧面积为3××2π×2+2+2=9π+12,
上、下底面的面积和为2××π×22=6π,
故这个几何体的表面积为9π+12+6π=15π+12.
