2021——2022学年人教版九年级数学下册第二十七章 相似单元测试题(word版含答案)
文档属性
| 名称 | 2021——2022学年人教版九年级数学下册第二十七章 相似单元测试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 322.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 16:51:38 | ||
图片预览



文档简介
第二十七章 相似
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知=,则的值为 ( )
A. B.
C. D.
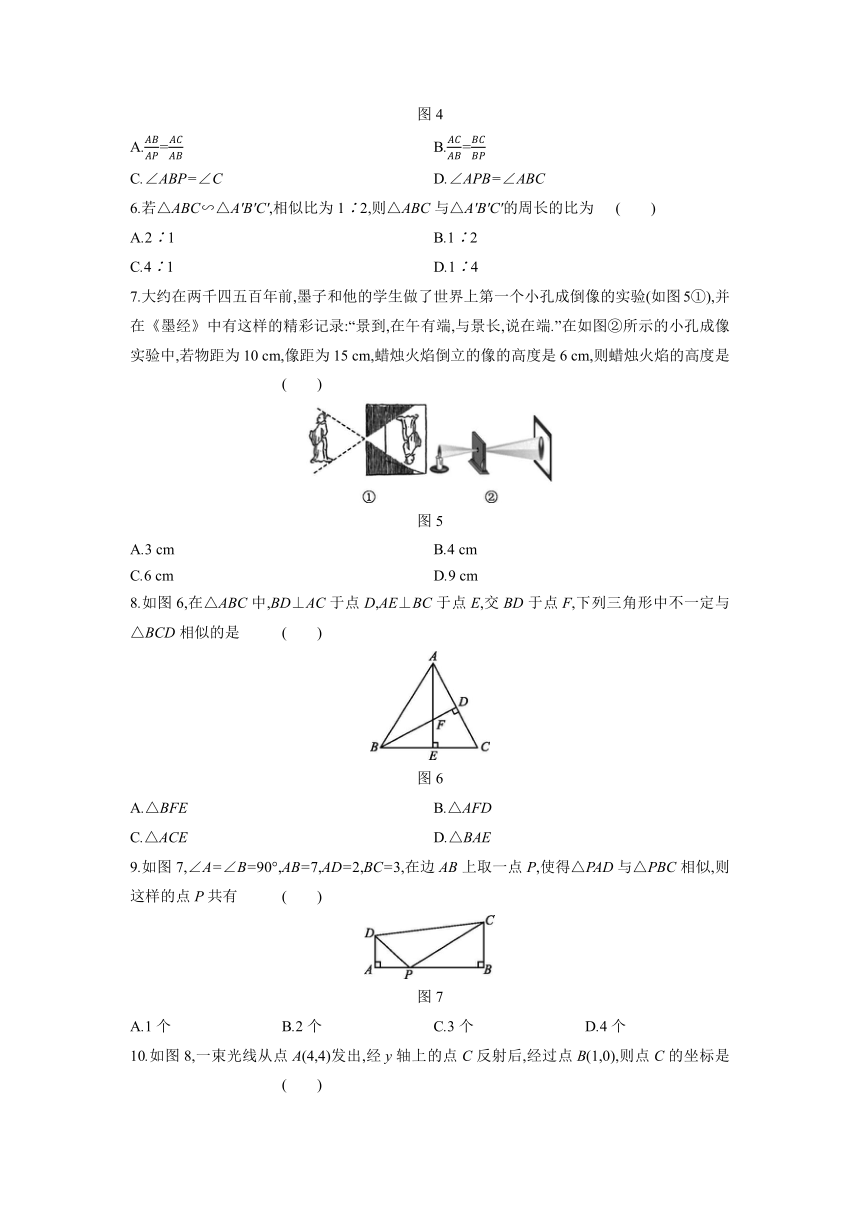
2.已知线段a,b,c,求作线段x,使x=,以下作法中正确的是 ( )
图1
3.如图2,在△ABC中,D,E分别是AB和AC的中点,S四边形BCED=15,则S△ABC等于 ( )
图2
A.30 B.25
C.22.5 D.20
4.如图3,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是 ( )
图3
A.= B.=
C.= D.=
5.如图4所示,P是△ABC的边AC上的一点,连接BP,以下条件中不能判定△ABP∽△ACB的是 ( )
图4
A.= B.=
C.∠ABP=∠C D.∠APB=∠ABC
6.若△ABC∽△A'B'C',相似比为1∶2,则△ABC与△A'B'C'的周长的比为 ( )
A.2∶1 B.1∶2
C.4∶1 D.1∶4
7.大约在两千四五百年前,墨子和他的学生做了世界上第一个小孔成倒像的实验(如图5①),并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端.”在如图②所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是 ( )
图5
A.3 cm B.4 cm
C.6 cm D.9 cm
8.如图6,在△ABC中,BD⊥AC于点D,AE⊥BC于点E,交BD于点F,下列三角形中不一定与△BCD相似的是 ( )
图6
A.△BFE B.△AFD
C.△ACE D.△BAE
9.如图7,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取一点P,使得△PAD与△PBC相似,则这样的点P共有 ( )
图7
A.1个 B.2个 C.3个 D.4个
10.如图8,一束光线从点A(4,4)发出,经y轴上的点C反射后,经过点B(1,0),则点C的坐标是 ( )
图8
A.0, B.0, C.(0,1) D.(0,2)
二、填空题(本大题共6小题,每小题3分,共18分)
11.若△ABC∽△A'B'C',∠A=35°,∠C'=85°,则∠B= °,∠B'= °.
12.若两个相似三角形的一组对应边长分别为3 cm和5 cm,且较小三角形的周长为15 cm,则较大三角形的周长为 cm.
13.如图9,☉O的半径为5,点P在☉O上,点A在☉O内,且PA=3,过点A作AP的垂线交☉O于点B,C.设PB=x,PC=y,则y与x之间的函数解析式为 .
图9
14.如图10所示,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时点O与竹竿的距离DO=6 m,竹竿与旗杆的距离DB=12 m,则旗杆AB的高为 m.
图10
15.如图11,已知矩形OABC与矩形ODEF是位似图形,P是位似中心.若点B的坐标为(1,2),点E的坐标为-,1,则点P的坐标为 .
图11
16.在 ABCD中,E是AD上一点,且点E将AD分为2∶3的两部分,连接BE,AC交于点F,则S△AEF∶S△CBF= .
三、解答题(本大题共7小题,共52分)
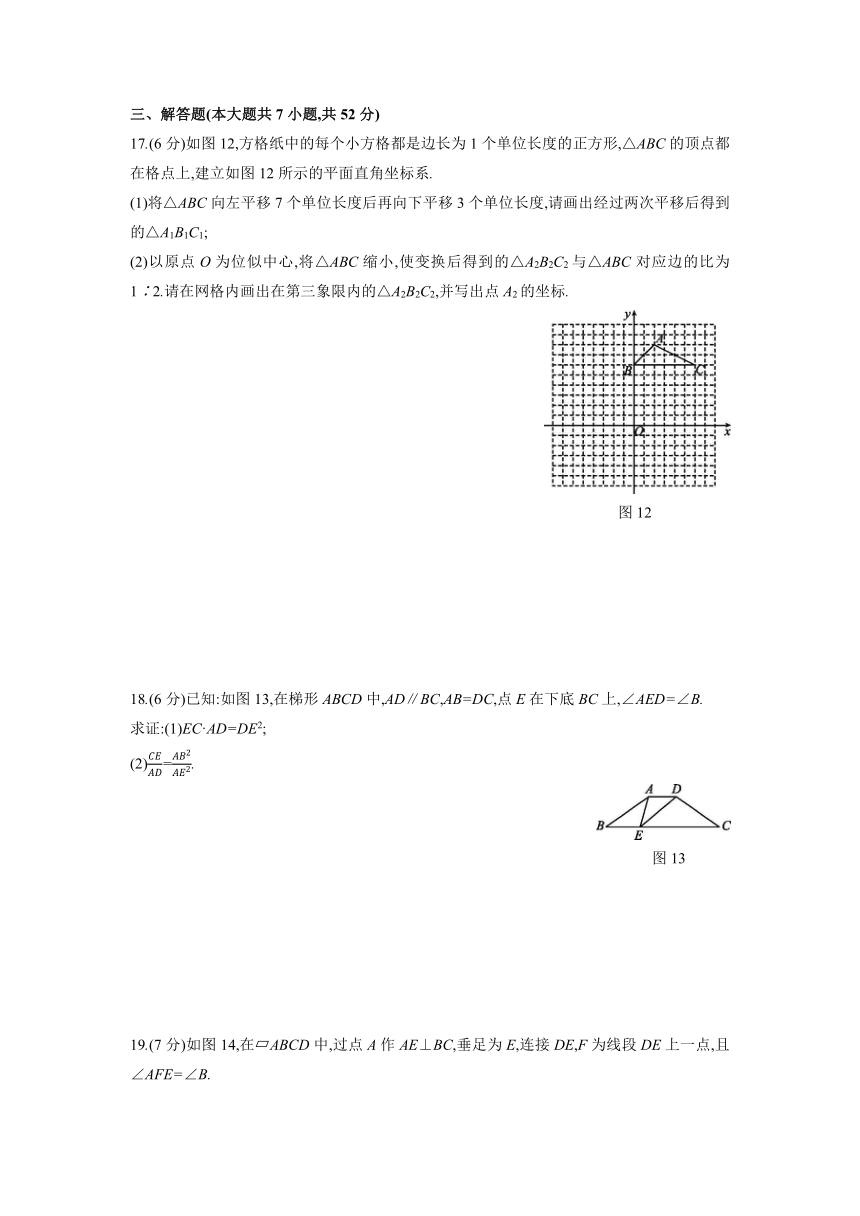
17.(6分)如图12,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图12所示的平面直角坐标系.
(1)将△ABC向左平移7个单位长度后再向下平移3个单位长度,请画出经过两次平移后得到的△A1B1C1;
(2)以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1∶2.请在网格内画出在第三象限内的△A2B2C2,并写出点A2的坐标.
图12
18.(6分)已知:如图13,在梯形ABCD中,AD∥BC,AB=DC,点E在下底BC上,∠AED=∠B.
求证:(1)EC·AD=DE2;
(2)=.
图13
19.(7分)如图14,在 ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
图14
20.(8分)如图15,已知AB是☉O的直径,直线BC与☉O相切于点B,过点A作AD∥OC交☉O于点D,连接CD.
(1)求证:CD是☉O的切线;
(2)若AD=4,直径AB=12,求线段BC的长.
图15
21.(8分)如图16,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADE∽△ACB;
(2)若=,求的值.
图16
22.(8分)如图17所示,BE是锐角三角形ABC的外接圆☉O的直径,CD是△ABC的高.
(1)求证:AC·BC=BE·CD;
(2)若CD=6,AD=8,BD=3,求☉O的直径BE.
图17
23.(9分)如图18,在Rt△ABC中,∠C=90°,BC=5 cm,AC=12 cm.点M在边AB上,以2 cm/s的速度由点B出发沿BA向点A匀速运动;同时点N在边AC上,以1 cm/s的速度由点A出发沿AC向点C匀速运动.当点M到达点A时,点M,N同时停止运动.连接MN,设点M运动的时间为t s.
(1)求AB的长.
(2)当t为何值时,△AMN的面积为△ABC面积的
(3)是否存在t值,使得以A,M,N为顶点的三角形与△ABC相似 若存在,请求出t的值;若不存在,请说明理由.
图18
答案
1.D [解析]由=,可得2y=5(x-2y),
解得5x=12y,
所以的值为.
2.B
3.D [解析]因为D,E分别是AB和AC的中点,所以DE∥BC且DE=BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知S△ADE∶S△ABC=1∶4,则S四边形BCED∶S△ABC=3∶4.题中已知S四边形BCED=15,故可得S△ABC=20,因此本题选D.
4.C [解析]∵EF∥BC,∴=.∵EG∥AB,∴=,∴=.因此本题选C.
5.B [解析]A项,符合两边成比例且夹角相等的两个三角形相似,能判定△ABP∽△ACB.
B项,成比例的两边所夹的角不一定相等,不能判定△ABP∽△ACB.
C项,符合两角分别相等的两个三角形相似,能判定△ABP∽△ACB.
D项,符合两角分别相等的两个三角形相似,能判定△ABP∽△ACB.故选B.
6.B
7.B [解析]设蜡烛火焰的高度是xcm,
由相似三角形的性质得到=,
解得x=4.
即蜡烛火焰的高度是4cm.
8.D [解析]∵BD⊥AC,AE⊥BC,
∴∠BDC=∠AEC=90°,
∴∠DBC+∠C=∠EAC+∠C=90°,
∴∠DBC=∠EAC,
∴△ACE∽△BCD.
∵∠ADF=∠BDC=90°,∠DAF=∠DBC,
∴△AFD∽△BCD.
∵∠EBF=∠DBC,∠BEF=∠BDC=90°,
∴△BFE∽△BCD,
∴一定与△BCD相似的是△BFE,△AFD,△ACE.
故不一定与△BCD相似的是△BAE.故选D.
9.C [解析]设AP=x,则有PB=AB-AP=7-x.若△PDA∽△CPB,则=,即=,解得x=1或x=6.若△PDA∽△PCB,则=,即=,解得x=.故这样的点P共有3个.故选C.
10.B [解析]过点A作AD⊥y轴于点D.
∵∠ADC=∠BOC=90°,∠ACD=∠BCO,
∴△OBC∽△DAC,∴=,∴=,解得OC=,∴点C的坐标为0,.故选B.
11.60 60 [解析]相似三角形的对应角相等,故∠A=∠A'=35°,∠C=∠C'=85°,所以∠B=∠B'=60°.
12.25
13.y= [解析]如图,连接PO并延长交☉O于点D,连接BD,
则∠C=∠D,∠PBD=90°.
∵PA⊥BC,
∴∠PAC=90°,
∴∠PAC=∠PBD,
∴△PAC∽△PBD,
∴=.
∵☉O的半径为5,PA=3,PB=x,PC=y,
∴=,∴y=.
14.9 [解析]由题意,得CD∥AB,
∴△OCD∽△OAB,∴=,
即=,解得AB=9(m).
15.(-1,0) [解析]∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点B的坐标为(1,2),点E的坐标为-,1,
∴EF=1,CO=2,FO=.
∵EF∥CO,
∴△PEF∽△PCO,
∴=,则=,
解得PF=,
故PO=+=1,
则点P的坐标为(-1,0).
16.4∶25或9∶25 [解析]在 ABCD中,
∵AD∥BC,∴△AEF∽△CBF.
如图①,当AE∶DE=2∶3时,AE∶AD=2∶5.
∵AD=BC,
∴AE∶BC=2∶5,
∴S△AEF∶S△CBF=4∶25;
如图②,当AE∶DE=3∶2时,AE∶AD=3∶5.
∵AD=BC,∴AE∶BC=3∶5,
∴S△AEF∶S△CBF=9∶25.
故答案为4∶25或9∶25.
17.解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示,点A2的坐标为(-1,-4).
18.证明:(1)∵在梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C,∠ADE=∠DEC.
∵∠AED=∠B,
∴∠C=∠AED,
∴△ADE∽△DEC,
∴=,
∴EC·AD=DE2.
(2)∵△ADE∽△DEC,
∴==,
∴·=·.
又∵AB=DC,
∴=.
19.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°.
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC.
(2)∵四边形ABCD是平行四边形,
∴DC=AB=8.
∵△ADF∽△DEC,
∴=,即=,
∴DE=12.
∵AD∥BC,AE⊥BC,
∴AE⊥AD.
在Rt△ADE中,∵∠EAD=90°,DE=12,AD=6,
∴AE===6.
20.解:(1)证明:连接OD,如图.
∵BC与☉O相切,
∴∠CBO=90°.
∵AD∥OC,
∴∠COB=∠A,∠COD=∠ODA.
∵OA=OD,∴∠A=∠ODA.
∴∠COB=∠COD.
又OB=OD,OC=OC,∴△COB≌△COD,
∴∠CDO=∠CBO=90°,即OD⊥CD.
又∵点D在☉O上,
∴CD是☉O的切线.
(2)连接BD,如图.
∵AB是☉O的直径,∴∠ADB=90°,
∴BD==8,∠OBC=∠ADB.
又∠COB=∠A,
∴△COB∽△BAD,
∴=,即=,
∴BC=12.
21.解:(1)证明:∵∠AED=∠B,∠DAE=∠CAB,∴△ADE∽△ACB.
(2)∵△ADE∽△ACB,∴∠ADF=∠C.
∵=,∴=,
∴△ADF∽△ACG,
∴==,∴==2.
22.解:(1)证明:连接CE.
由BE为☉O的直径知∠ECB=90°.
∵CD是△ABC的高,
∴CD⊥AB,
∴∠ADC=90°=∠ECB.
又∵∠A=∠E,
∴△ADC∽△ECB,
∴=,
∴AC·BC=BE·CD.
(2)由勾股定理,知AC==10,BC==3.
又∵AC·BC=BE·CD,
∴10×3=6BE,解得BE=5.
解:(1)在Rt△ABC中,BC=5cm,AC=12cm,由勾股定理,得
AB===13(cm).
(2)如图,过点M作MH⊥AC于点H,
则MH∥BC,
∴△AMH∽△ABC,
∴=.
由题意,得BM=2tcm,AN=tcm,则AM=(13-2t)cm,
∴=,解得MH=(cm).
由题意,得·t·=×5×12×,
解得t1=2,t2=.
答:当t的值为2或时,△AMN的面积为△ABC面积的.
(3)存在.
由题意可知分两种情况.
①若△AMN∽△ABC,则=,
∴=,解得t=.
②若△ANM∽△ABC,则=,
∴=,解得t=.
综上,当t的值为或时,以A,M,N为顶点的三角形与△ABC相似.
一、选择题(本大题共10小题,每小题3分,共30分)
1.已知=,则的值为 ( )
A. B.
C. D.
2.已知线段a,b,c,求作线段x,使x=,以下作法中正确的是 ( )
图1
3.如图2,在△ABC中,D,E分别是AB和AC的中点,S四边形BCED=15,则S△ABC等于 ( )
图2
A.30 B.25
C.22.5 D.20
4.如图3,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是 ( )
图3
A.= B.=
C.= D.=
5.如图4所示,P是△ABC的边AC上的一点,连接BP,以下条件中不能判定△ABP∽△ACB的是 ( )
图4
A.= B.=
C.∠ABP=∠C D.∠APB=∠ABC
6.若△ABC∽△A'B'C',相似比为1∶2,则△ABC与△A'B'C'的周长的比为 ( )
A.2∶1 B.1∶2
C.4∶1 D.1∶4
7.大约在两千四五百年前,墨子和他的学生做了世界上第一个小孔成倒像的实验(如图5①),并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端.”在如图②所示的小孔成像实验中,若物距为10 cm,像距为15 cm,蜡烛火焰倒立的像的高度是6 cm,则蜡烛火焰的高度是 ( )
图5
A.3 cm B.4 cm
C.6 cm D.9 cm
8.如图6,在△ABC中,BD⊥AC于点D,AE⊥BC于点E,交BD于点F,下列三角形中不一定与△BCD相似的是 ( )
图6
A.△BFE B.△AFD
C.△ACE D.△BAE
9.如图7,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取一点P,使得△PAD与△PBC相似,则这样的点P共有 ( )
图7
A.1个 B.2个 C.3个 D.4个
10.如图8,一束光线从点A(4,4)发出,经y轴上的点C反射后,经过点B(1,0),则点C的坐标是 ( )
图8
A.0, B.0, C.(0,1) D.(0,2)
二、填空题(本大题共6小题,每小题3分,共18分)
11.若△ABC∽△A'B'C',∠A=35°,∠C'=85°,则∠B= °,∠B'= °.
12.若两个相似三角形的一组对应边长分别为3 cm和5 cm,且较小三角形的周长为15 cm,则较大三角形的周长为 cm.
13.如图9,☉O的半径为5,点P在☉O上,点A在☉O内,且PA=3,过点A作AP的垂线交☉O于点B,C.设PB=x,PC=y,则y与x之间的函数解析式为 .
图9
14.如图10所示,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好在地面的同一点O,此时点O与竹竿的距离DO=6 m,竹竿与旗杆的距离DB=12 m,则旗杆AB的高为 m.
图10
15.如图11,已知矩形OABC与矩形ODEF是位似图形,P是位似中心.若点B的坐标为(1,2),点E的坐标为-,1,则点P的坐标为 .
图11
16.在 ABCD中,E是AD上一点,且点E将AD分为2∶3的两部分,连接BE,AC交于点F,则S△AEF∶S△CBF= .
三、解答题(本大题共7小题,共52分)
17.(6分)如图12,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图12所示的平面直角坐标系.
(1)将△ABC向左平移7个单位长度后再向下平移3个单位长度,请画出经过两次平移后得到的△A1B1C1;
(2)以原点O为位似中心,将△ABC缩小,使变换后得到的△A2B2C2与△ABC对应边的比为1∶2.请在网格内画出在第三象限内的△A2B2C2,并写出点A2的坐标.
图12
18.(6分)已知:如图13,在梯形ABCD中,AD∥BC,AB=DC,点E在下底BC上,∠AED=∠B.
求证:(1)EC·AD=DE2;
(2)=.
图13
19.(7分)如图14,在 ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
图14
20.(8分)如图15,已知AB是☉O的直径,直线BC与☉O相切于点B,过点A作AD∥OC交☉O于点D,连接CD.
(1)求证:CD是☉O的切线;
(2)若AD=4,直径AB=12,求线段BC的长.
图15
21.(8分)如图16,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADE∽△ACB;
(2)若=,求的值.
图16
22.(8分)如图17所示,BE是锐角三角形ABC的外接圆☉O的直径,CD是△ABC的高.
(1)求证:AC·BC=BE·CD;
(2)若CD=6,AD=8,BD=3,求☉O的直径BE.
图17
23.(9分)如图18,在Rt△ABC中,∠C=90°,BC=5 cm,AC=12 cm.点M在边AB上,以2 cm/s的速度由点B出发沿BA向点A匀速运动;同时点N在边AC上,以1 cm/s的速度由点A出发沿AC向点C匀速运动.当点M到达点A时,点M,N同时停止运动.连接MN,设点M运动的时间为t s.
(1)求AB的长.
(2)当t为何值时,△AMN的面积为△ABC面积的
(3)是否存在t值,使得以A,M,N为顶点的三角形与△ABC相似 若存在,请求出t的值;若不存在,请说明理由.
图18
答案
1.D [解析]由=,可得2y=5(x-2y),
解得5x=12y,
所以的值为.
2.B
3.D [解析]因为D,E分别是AB和AC的中点,所以DE∥BC且DE=BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知S△ADE∶S△ABC=1∶4,则S四边形BCED∶S△ABC=3∶4.题中已知S四边形BCED=15,故可得S△ABC=20,因此本题选D.
4.C [解析]∵EF∥BC,∴=.∵EG∥AB,∴=,∴=.因此本题选C.
5.B [解析]A项,符合两边成比例且夹角相等的两个三角形相似,能判定△ABP∽△ACB.
B项,成比例的两边所夹的角不一定相等,不能判定△ABP∽△ACB.
C项,符合两角分别相等的两个三角形相似,能判定△ABP∽△ACB.
D项,符合两角分别相等的两个三角形相似,能判定△ABP∽△ACB.故选B.
6.B
7.B [解析]设蜡烛火焰的高度是xcm,
由相似三角形的性质得到=,
解得x=4.
即蜡烛火焰的高度是4cm.
8.D [解析]∵BD⊥AC,AE⊥BC,
∴∠BDC=∠AEC=90°,
∴∠DBC+∠C=∠EAC+∠C=90°,
∴∠DBC=∠EAC,
∴△ACE∽△BCD.
∵∠ADF=∠BDC=90°,∠DAF=∠DBC,
∴△AFD∽△BCD.
∵∠EBF=∠DBC,∠BEF=∠BDC=90°,
∴△BFE∽△BCD,
∴一定与△BCD相似的是△BFE,△AFD,△ACE.
故不一定与△BCD相似的是△BAE.故选D.
9.C [解析]设AP=x,则有PB=AB-AP=7-x.若△PDA∽△CPB,则=,即=,解得x=1或x=6.若△PDA∽△PCB,则=,即=,解得x=.故这样的点P共有3个.故选C.
10.B [解析]过点A作AD⊥y轴于点D.
∵∠ADC=∠BOC=90°,∠ACD=∠BCO,
∴△OBC∽△DAC,∴=,∴=,解得OC=,∴点C的坐标为0,.故选B.
11.60 60 [解析]相似三角形的对应角相等,故∠A=∠A'=35°,∠C=∠C'=85°,所以∠B=∠B'=60°.
12.25
13.y= [解析]如图,连接PO并延长交☉O于点D,连接BD,
则∠C=∠D,∠PBD=90°.
∵PA⊥BC,
∴∠PAC=90°,
∴∠PAC=∠PBD,
∴△PAC∽△PBD,
∴=.
∵☉O的半径为5,PA=3,PB=x,PC=y,
∴=,∴y=.
14.9 [解析]由题意,得CD∥AB,
∴△OCD∽△OAB,∴=,
即=,解得AB=9(m).
15.(-1,0) [解析]∵矩形OABC与矩形ODEF是位似图形,P是位似中心,点B的坐标为(1,2),点E的坐标为-,1,
∴EF=1,CO=2,FO=.
∵EF∥CO,
∴△PEF∽△PCO,
∴=,则=,
解得PF=,
故PO=+=1,
则点P的坐标为(-1,0).
16.4∶25或9∶25 [解析]在 ABCD中,
∵AD∥BC,∴△AEF∽△CBF.
如图①,当AE∶DE=2∶3时,AE∶AD=2∶5.
∵AD=BC,
∴AE∶BC=2∶5,
∴S△AEF∶S△CBF=4∶25;
如图②,当AE∶DE=3∶2时,AE∶AD=3∶5.
∵AD=BC,∴AE∶BC=3∶5,
∴S△AEF∶S△CBF=9∶25.
故答案为4∶25或9∶25.
17.解:(1)△A1B1C1如图所示.
(2)△A2B2C2如图所示,点A2的坐标为(-1,-4).
18.证明:(1)∵在梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠C,∠ADE=∠DEC.
∵∠AED=∠B,
∴∠C=∠AED,
∴△ADE∽△DEC,
∴=,
∴EC·AD=DE2.
(2)∵△ADE∽△DEC,
∴==,
∴·=·.
又∵AB=DC,
∴=.
19.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°.
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC.
(2)∵四边形ABCD是平行四边形,
∴DC=AB=8.
∵△ADF∽△DEC,
∴=,即=,
∴DE=12.
∵AD∥BC,AE⊥BC,
∴AE⊥AD.
在Rt△ADE中,∵∠EAD=90°,DE=12,AD=6,
∴AE===6.
20.解:(1)证明:连接OD,如图.
∵BC与☉O相切,
∴∠CBO=90°.
∵AD∥OC,
∴∠COB=∠A,∠COD=∠ODA.
∵OA=OD,∴∠A=∠ODA.
∴∠COB=∠COD.
又OB=OD,OC=OC,∴△COB≌△COD,
∴∠CDO=∠CBO=90°,即OD⊥CD.
又∵点D在☉O上,
∴CD是☉O的切线.
(2)连接BD,如图.
∵AB是☉O的直径,∴∠ADB=90°,
∴BD==8,∠OBC=∠ADB.
又∠COB=∠A,
∴△COB∽△BAD,
∴=,即=,
∴BC=12.
21.解:(1)证明:∵∠AED=∠B,∠DAE=∠CAB,∴△ADE∽△ACB.
(2)∵△ADE∽△ACB,∴∠ADF=∠C.
∵=,∴=,
∴△ADF∽△ACG,
∴==,∴==2.
22.解:(1)证明:连接CE.
由BE为☉O的直径知∠ECB=90°.
∵CD是△ABC的高,
∴CD⊥AB,
∴∠ADC=90°=∠ECB.
又∵∠A=∠E,
∴△ADC∽△ECB,
∴=,
∴AC·BC=BE·CD.
(2)由勾股定理,知AC==10,BC==3.
又∵AC·BC=BE·CD,
∴10×3=6BE,解得BE=5.
解:(1)在Rt△ABC中,BC=5cm,AC=12cm,由勾股定理,得
AB===13(cm).
(2)如图,过点M作MH⊥AC于点H,
则MH∥BC,
∴△AMH∽△ABC,
∴=.
由题意,得BM=2tcm,AN=tcm,则AM=(13-2t)cm,
∴=,解得MH=(cm).
由题意,得·t·=×5×12×,
解得t1=2,t2=.
答:当t的值为2或时,△AMN的面积为△ABC面积的.
(3)存在.
由题意可知分两种情况.
①若△AMN∽△ABC,则=,
∴=,解得t=.
②若△ANM∽△ABC,则=,
∴=,解得t=.
综上,当t的值为或时,以A,M,N为顶点的三角形与△ABC相似.
