2021-2022学年沪科版九年级数学上册 21.1 二次函数 同步测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册 21.1 二次函数 同步测试卷 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 44.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 20:41:11 | ||
图片预览

文档简介
21.1 二次函数同步测试卷 2021-2022学年沪科版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共5小题,共25分)
下列函数中,y关于x的二次函数是( )
A. B.
C. D.
若y=(a-2)-3x+2是二次函数,则a的取值范围是( )
A. B. C. D.
若函数y=+1的函数值为5,则自变量x的值应为( )
A. B. C. D.
用一段20米长的铁丝在平地上围成一个长方形,则长方形的面积y(平方米)和长方形的一边长x(米)的关系式为( )
A. B. C. D.
在RtABC中,C=,BC=a,AC=b,AB=c,若a+b =5,则RtABC的面积S关于边长c的函数关系式为( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
已知二次函数y=1-5x+,则二次项系数a= ,一次项系数b= ,常数项c= .
如果函数y= ( k-3)+7x+2是关于x的二次函数,那么k的值是 .
一台机器原价为60万元,如果每年价格的下降率为x,两年后这台机器的价格为y万元,则y关于x的函数关系式为 .
某企业因生产转型,二月份产值比一月份下降20%,转型成功后生产呈现良好上升势头,三、四月份稳步增长,月平均增长率为x.设该企业一月份的产值为a,则该企业四月份的产值y关于x的函数表达式为 (不用体现自变量的取值范围).
三、解答题(本大题共6小题,共55分)
已知y与成正比例,且当x=3时,y=-18,写出y与x之间的函数解析式,它是二次函数吗
某大型超市将进价为40元/套的某种服装按50元/套售出时,每天可以售出300套,据市场调查发现,这种服装售价每提高1元,销售量就减少5套,如果超市将售价定为x元/套(x50),请你求出每天的销售利润y元与售价x元/套之间的函数表达式.
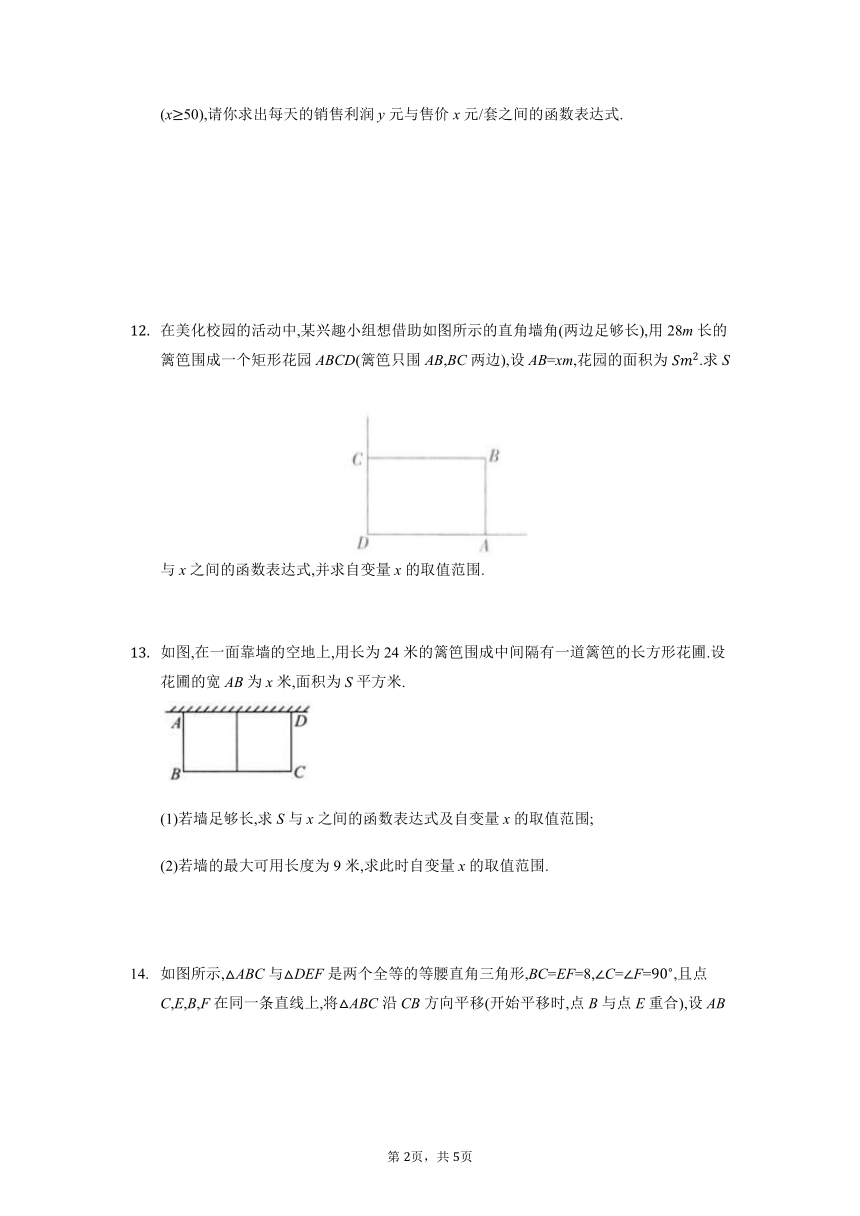
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为.求S与x之间的函数表达式,并求自变量x的取值范围.
如图,在一面靠墙的空地上,用长为24米的篱笆围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)若墙足够长,求S与x之间的函数表达式及自变量x的取值范围;
(2)若墙的最大可用长度为9米,求此时自变量x的取值范围.
如图所示,ABC与DEF是两个全等的等腰直角三角形,BC=EF=8,C=F=,且点C,E,B,F在同一条直线上,将ABC沿CB方向平移(开始平移时,点B与点E重合),设AB与DE相交于点P,当点C与点E重合时,停止平移,设CE=x,PBE的面积为S,求:
(1)S与x之间的函数表达式,并指出自变量的取值范围;
(2)当x=3时,求PBE的面积.
如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,求出发时间t秒与BPQ的面积S平方厘米的函数关系式,并写出t的取值范围.
参考答案
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】A
6.【答案】3 -5 1
7.【答案】0
8.【答案】 y=60
9.【答案】y=0.8 +1.6ax+0.8a
10.【答案】解:y与成正比例,
设y=(k0),
当x=3时,y=-18,
-18=k,
k=-2,
y与x之间的函数解析式为y=-.
y=-符合二次函数的定义,属于二次函数.
11.【答案】解:根据题意可得,
y=(x-40)[300-5(x-50)]=(x-40)(550-5x)=-+750x-22000 ( x50).
12.【答案】解:AB=xm,
BC=(28-x)m,
则S=ABBC=x(28-x)=-+28x,
篱笆的长为28m,
,
即S
13.【答案】解:(1)S=BCAB=(24-3x)x=-+24x.
由题意得
解得0< x<8.
S=-+24x(0< x<8).
(2)由题意,得24-3x9,
x5.
结合(1)得x的取值范围是5x<8.
14.【答案】解:(1)CE=x,BC=8,
EB=8-x.
ABC与DEF是两个全等的等腰直角三角形,
ABC=DEF=,
PBE是等腰直角三角形,
则易得PB=PE=EB=(8-x),
S=PBPE=(8-x)(8-x)==-4x+16,
即S=-4x+16.
由题意,得0<8-x8,
0x<8.
(2)当x=3时,S==.
15.【答案】易知PB=(6-t)厘米,BQ=BE+EQ=(6+t)厘米,
S=PBBQ=(6-t)(6+t)=-+18,
S=-+18(0t<6).
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共5小题,共25分)
下列函数中,y关于x的二次函数是( )
A. B.
C. D.
若y=(a-2)-3x+2是二次函数,则a的取值范围是( )
A. B. C. D.
若函数y=+1的函数值为5,则自变量x的值应为( )
A. B. C. D.
用一段20米长的铁丝在平地上围成一个长方形,则长方形的面积y(平方米)和长方形的一边长x(米)的关系式为( )
A. B. C. D.
在RtABC中,C=,BC=a,AC=b,AB=c,若a+b =5,则RtABC的面积S关于边长c的函数关系式为( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
已知二次函数y=1-5x+,则二次项系数a= ,一次项系数b= ,常数项c= .
如果函数y= ( k-3)+7x+2是关于x的二次函数,那么k的值是 .
一台机器原价为60万元,如果每年价格的下降率为x,两年后这台机器的价格为y万元,则y关于x的函数关系式为 .
某企业因生产转型,二月份产值比一月份下降20%,转型成功后生产呈现良好上升势头,三、四月份稳步增长,月平均增长率为x.设该企业一月份的产值为a,则该企业四月份的产值y关于x的函数表达式为 (不用体现自变量的取值范围).
三、解答题(本大题共6小题,共55分)
已知y与成正比例,且当x=3时,y=-18,写出y与x之间的函数解析式,它是二次函数吗
某大型超市将进价为40元/套的某种服装按50元/套售出时,每天可以售出300套,据市场调查发现,这种服装售价每提高1元,销售量就减少5套,如果超市将售价定为x元/套(x50),请你求出每天的销售利润y元与售价x元/套之间的函数表达式.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为.求S与x之间的函数表达式,并求自变量x的取值范围.
如图,在一面靠墙的空地上,用长为24米的篱笆围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
(1)若墙足够长,求S与x之间的函数表达式及自变量x的取值范围;
(2)若墙的最大可用长度为9米,求此时自变量x的取值范围.
如图所示,ABC与DEF是两个全等的等腰直角三角形,BC=EF=8,C=F=,且点C,E,B,F在同一条直线上,将ABC沿CB方向平移(开始平移时,点B与点E重合),设AB与DE相交于点P,当点C与点E重合时,停止平移,设CE=x,PBE的面积为S,求:
(1)S与x之间的函数表达式,并指出自变量的取值范围;
(2)当x=3时,求PBE的面积.
如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,求出发时间t秒与BPQ的面积S平方厘米的函数关系式,并写出t的取值范围.
参考答案
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】C
5.【答案】A
6.【答案】3 -5 1
7.【答案】0
8.【答案】 y=60
9.【答案】y=0.8 +1.6ax+0.8a
10.【答案】解:y与成正比例,
设y=(k0),
当x=3时,y=-18,
-18=k,
k=-2,
y与x之间的函数解析式为y=-.
y=-符合二次函数的定义,属于二次函数.
11.【答案】解:根据题意可得,
y=(x-40)[300-5(x-50)]=(x-40)(550-5x)=-+750x-22000 ( x50).
12.【答案】解:AB=xm,
BC=(28-x)m,
则S=ABBC=x(28-x)=-+28x,
篱笆的长为28m,
,
即S
13.【答案】解:(1)S=BCAB=(24-3x)x=-+24x.
由题意得
解得0< x<8.
S=-+24x(0< x<8).
(2)由题意,得24-3x9,
x5.
结合(1)得x的取值范围是5x<8.
14.【答案】解:(1)CE=x,BC=8,
EB=8-x.
ABC与DEF是两个全等的等腰直角三角形,
ABC=DEF=,
PBE是等腰直角三角形,
则易得PB=PE=EB=(8-x),
S=PBPE=(8-x)(8-x)==-4x+16,
即S=-4x+16.
由题意,得0<8-x8,
0x<8.
(2)当x=3时,S==.
15.【答案】易知PB=(6-t)厘米,BQ=BE+EQ=(6+t)厘米,
S=PBBQ=(6-t)(6+t)=-+18,
S=-+18(0t<6).
第2页,共2页
