甘肃省白银市靖远县第二高级中学2021-2022学年高二上学期期中考试(一)数学试卷(Word版含答案)
文档属性
| 名称 | 甘肃省白银市靖远县第二高级中学2021-2022学年高二上学期期中考试(一)数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 619.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-22 21:27:49 | ||
图片预览


文档简介
靖远县第二高级中学2021-2022学年度第一学期期中考试
高二数学
时间:120分钟 分值:150分
一、单选题(每小题5分,共60分)
1.等差数列中,已知,,当时,则序号等于( )
A.90 B.96 C.98 D.100
2.对于任意实数给定下列命题正确的是( )
A.若,则 B.若则
C.若则 D.若则
3.在中,,,,则A为( )
A.或 B. C.或 D.
4.已知数列{an}是等比数列,其前n项和为Sn,则下列结论正确的是( )
A.若a1+a2>0,则a1+a3>0 B.若a1+a3>0,则a1+a2>0
C.若a1>0,则S2021>0 D.若a1>0,则S2020>0
5.在中,,,,则的面积为( )
A.15 B. C.40 D.
6.不等式组的解集为( )
A. B. C. D.
7.在中,已知,那么一定是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.形状无法确定
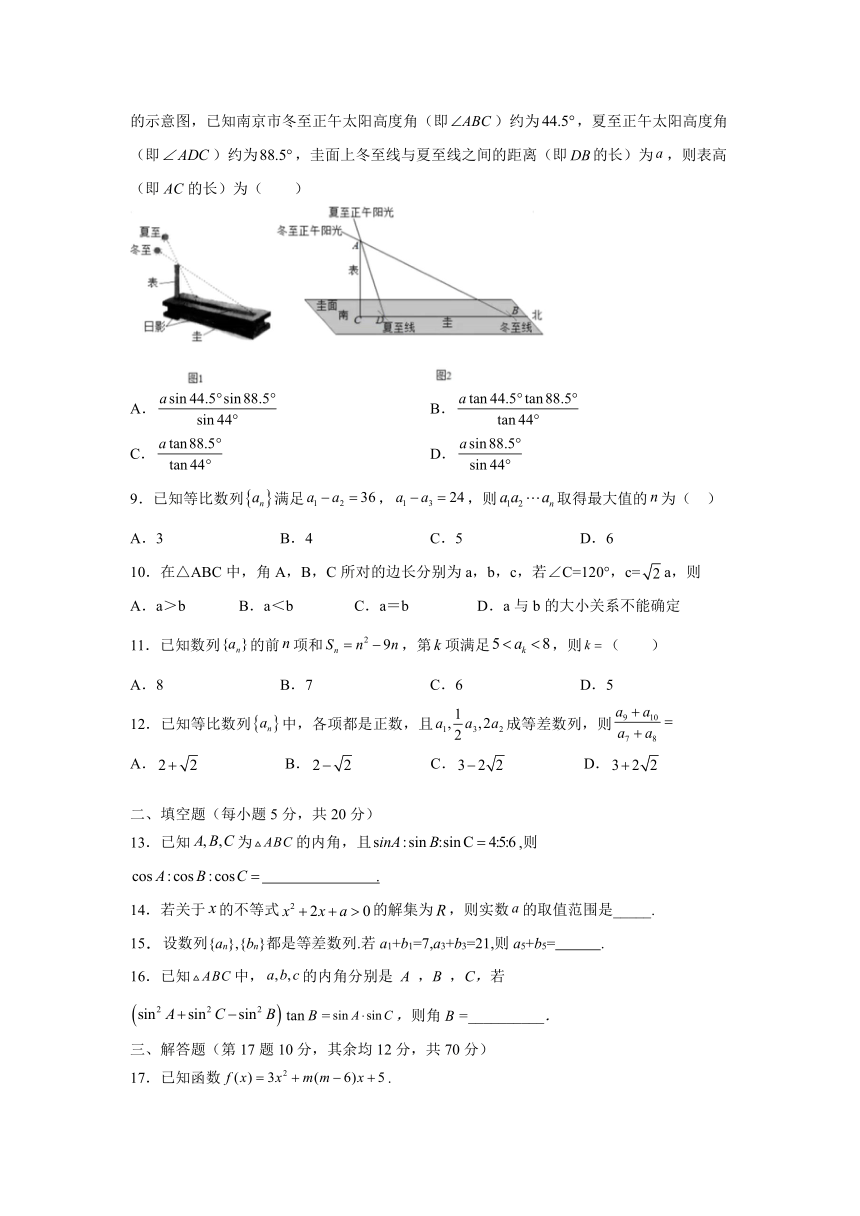
8.圭表(如图)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为“表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为“圭”).当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图是一个根据南京市的地理位置设计的圭表的示意图,已知南京市冬至正午太阳高度角(即)约为,夏至正午太阳高度角(即)约为,圭面上冬至线与夏至线之间的距离(即的长)为,则表高(即的长)为( )
A. B.
C. D.
9.已知等比数列满足,,则取得最大值的为( )
A.3 B.4 C.5 D.6
10.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=a,则
A.a>b B.a<b C.a=b D.a与b的大小关系不能确定
11.已知数列的前项和,第项满足,则( )
A.8 B.7 C.6 D.5
12.已知等比数列中,各项都是正数,且成等差数列,则
A. B. C. D.
二、填空题(每小题5分,共20分)
13.已知为的内角,且,则 .
14.若关于的不等式的解集为,则实数的取值范围是_____.
15.设数列{an},{bn}都是等差数列.若a1+b1=7,a3+b3=21,则a5+b5= .
16.已知中,的内角分别是 A ,B ,C,若=,则角B =__________.
三、解答题(第17题10分,其余均12分,共70分)
17.已知函数.
(1)若,求实数的取值范围;
(2)若关于的不等式的解集为(-1,4),求实数,的值.
18.如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.
(1)求cos∠CBE的值;
(2)求AE.
19.已知等差数列满足,.
(1)求的通项公式;
(2)设是等比数列的前n项和,若,,求.
20.在 中, , , 分别是角 , , 的对边, , .
(1)求 的面积;
(2)若 ,求角 .
21.设数列前项和为,满足.
(1)求数列的通项公式;
(2)令,求数列的前项和.
22.在△ABC中,角A,B,C所对的边分别为a,b,c,满足cos C+cos Acos B=2sin Acos B.
(1)求cos B的值;
(2)若a+c=2,求b的取值范围.
高二期中考试参考答案
一、选择题
1-5 DCCCB 6-10 CAABA 11-12 AD
二、填空题
13. 14. 15.35 16.或
17.(1)或;(2),.
【详解】
(1)由已知,∴
得或;
(2)∵,∴
由-1,4是方程的两根,得
,∴,.
18.(1)因为,所以,.
(2)在中,,由正弦定理得,
故
19.(1);(2),或.
【详解】
(1)设等差数列的公差为d,∵.∴,
,解得,,∴.
(2)设等比数列的公比为q,,,联立解得,,∴,或.
20.(1)14;(2) .
【详解】
(1)∵ , ,
∴ ,∵ ,∴ ,∴
(2) , ,∴
由余弦定理得,
∴ ,由正弦定理: ,∴
∵ 且 为锐角,∴ 一定是锐角,
∴
21.(1);(2).
【详解】
(1)
两式相减,得.
所以,,
又,即∴
∴是首项为2,公比是4的等比数列.
.
(2).
①
②
①-②,得,
故.
22.(1);(2).
【详解】
(1)因为cos C+cos Acos B=sin Acos B,
所以-cos(A+B)+cos Acos B=sin Acos B,
即sin Asin B=sin Acos B,
因为sin A≠0,所以sin B=cos B>0,
又因为sin 2B+cos 2B=1,解得cos B=.
(2)由a+c=2,可得c=2-a,
由余弦定理,得
b2=a2+c2-2accos B=a2+c2-ac=a2+(2-a)2-a(2-a)=(a-1)2+,
因为0所以b的取值范围为.
高二数学
时间:120分钟 分值:150分
一、单选题(每小题5分,共60分)
1.等差数列中,已知,,当时,则序号等于( )
A.90 B.96 C.98 D.100
2.对于任意实数给定下列命题正确的是( )
A.若,则 B.若则
C.若则 D.若则
3.在中,,,,则A为( )
A.或 B. C.或 D.
4.已知数列{an}是等比数列,其前n项和为Sn,则下列结论正确的是( )
A.若a1+a2>0,则a1+a3>0 B.若a1+a3>0,则a1+a2>0
C.若a1>0,则S2021>0 D.若a1>0,则S2020>0
5.在中,,,,则的面积为( )
A.15 B. C.40 D.
6.不等式组的解集为( )
A. B. C. D.
7.在中,已知,那么一定是( )
A.等腰三角形 B.直角三角形 C.等边三角形 D.形状无法确定
8.圭表(如图)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为“表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为“圭”).当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图是一个根据南京市的地理位置设计的圭表的示意图,已知南京市冬至正午太阳高度角(即)约为,夏至正午太阳高度角(即)约为,圭面上冬至线与夏至线之间的距离(即的长)为,则表高(即的长)为( )
A. B.
C. D.
9.已知等比数列满足,,则取得最大值的为( )
A.3 B.4 C.5 D.6
10.在△ABC中,角A,B,C所对的边长分别为a,b,c,若∠C=120°,c=a,则
A.a>b B.a<b C.a=b D.a与b的大小关系不能确定
11.已知数列的前项和,第项满足,则( )
A.8 B.7 C.6 D.5
12.已知等比数列中,各项都是正数,且成等差数列,则
A. B. C. D.
二、填空题(每小题5分,共20分)
13.已知为的内角,且,则 .
14.若关于的不等式的解集为,则实数的取值范围是_____.
15.设数列{an},{bn}都是等差数列.若a1+b1=7,a3+b3=21,则a5+b5= .
16.已知中,的内角分别是 A ,B ,C,若=,则角B =__________.
三、解答题(第17题10分,其余均12分,共70分)
17.已知函数.
(1)若,求实数的取值范围;
(2)若关于的不等式的解集为(-1,4),求实数,的值.
18.如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.
(1)求cos∠CBE的值;
(2)求AE.
19.已知等差数列满足,.
(1)求的通项公式;
(2)设是等比数列的前n项和,若,,求.
20.在 中, , , 分别是角 , , 的对边, , .
(1)求 的面积;
(2)若 ,求角 .
21.设数列前项和为,满足.
(1)求数列的通项公式;
(2)令,求数列的前项和.
22.在△ABC中,角A,B,C所对的边分别为a,b,c,满足cos C+cos Acos B=2sin Acos B.
(1)求cos B的值;
(2)若a+c=2,求b的取值范围.
高二期中考试参考答案
一、选择题
1-5 DCCCB 6-10 CAABA 11-12 AD
二、填空题
13. 14. 15.35 16.或
17.(1)或;(2),.
【详解】
(1)由已知,∴
得或;
(2)∵,∴
由-1,4是方程的两根,得
,∴,.
18.(1)因为,所以,.
(2)在中,,由正弦定理得,
故
19.(1);(2),或.
【详解】
(1)设等差数列的公差为d,∵.∴,
,解得,,∴.
(2)设等比数列的公比为q,,,联立解得,,∴,或.
20.(1)14;(2) .
【详解】
(1)∵ , ,
∴ ,∵ ,∴ ,∴
(2) , ,∴
由余弦定理得,
∴ ,由正弦定理: ,∴
∵ 且 为锐角,∴ 一定是锐角,
∴
21.(1);(2).
【详解】
(1)
两式相减,得.
所以,,
又,即∴
∴是首项为2,公比是4的等比数列.
.
(2).
①
②
①-②,得,
故.
22.(1);(2).
【详解】
(1)因为cos C+cos Acos B=sin Acos B,
所以-cos(A+B)+cos Acos B=sin Acos B,
即sin Asin B=sin Acos B,
因为sin A≠0,所以sin B=cos B>0,
又因为sin 2B+cos 2B=1,解得cos B=.
(2)由a+c=2,可得c=2-a,
由余弦定理,得
b2=a2+c2-2accos B=a2+c2-ac=a2+(2-a)2-a(2-a)=(a-1)2+,
因为0
同课章节目录
