选修1-2,2-2推理与证明 的教材分析及教学指导
文档属性
| 名称 | 选修1-2,2-2推理与证明 的教材分析及教学指导 |  | |
| 格式 | zip | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-02 20:18:35 | ||
图片预览










文档简介
(共41张PPT)
普通高中课程标准实验教科书
(A版)
选修1-2,2-2
推理与证明
一、内容结构
二、教学目标
三、教材特点与教学建议
四、需要注意的问题
一、内容结构
“推理与证明”是数学的基本思维过程,也是人们学习和生活中经常使用的思维方式.推理一般包括合情推理和演绎推理.在本章中,学生将通过对已学知识的回顾,进一步体会合情推理、演绎推理以及二者之间的联系与差异;体会数学证明的特点,了解数学证明的基本方法,包括直接证明的方法(如分析法、综合法、数学归纳法)和间接证明的方法(如反证法);感受逻辑证明在数学以及日常生活中的作用,养成言之有理、论证有据的习惯。
文科(10课时)
2.1合情推理与演绎推理 约5课时
2.2直接证明与间接证明 约4课时
小结 约1课时
理科(8课时)
2.1合情推理与演绎推理 约3课时
2.2直接证明与间接证明 约3课时
2.3数学归纳法 约2课时
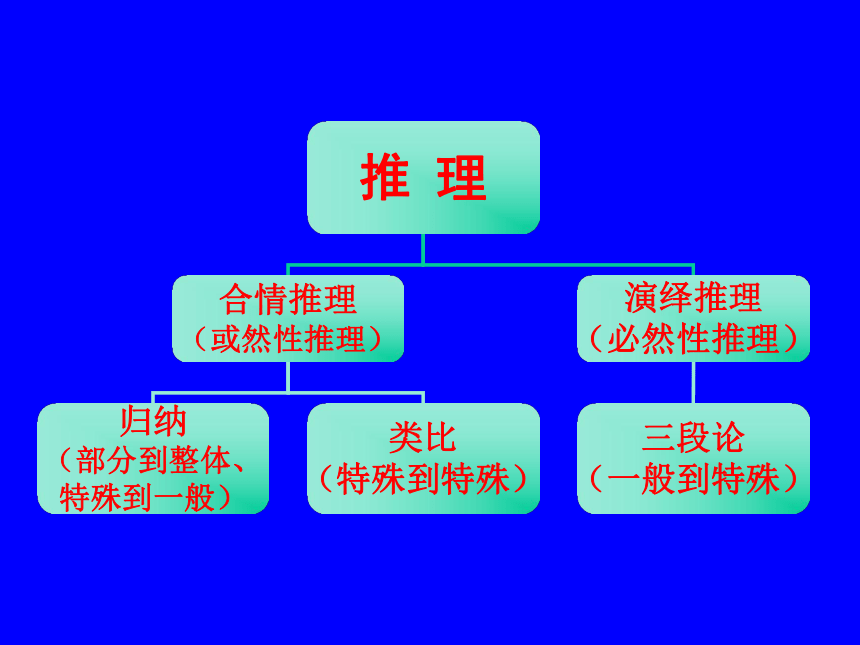
推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(部分到整体、
特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
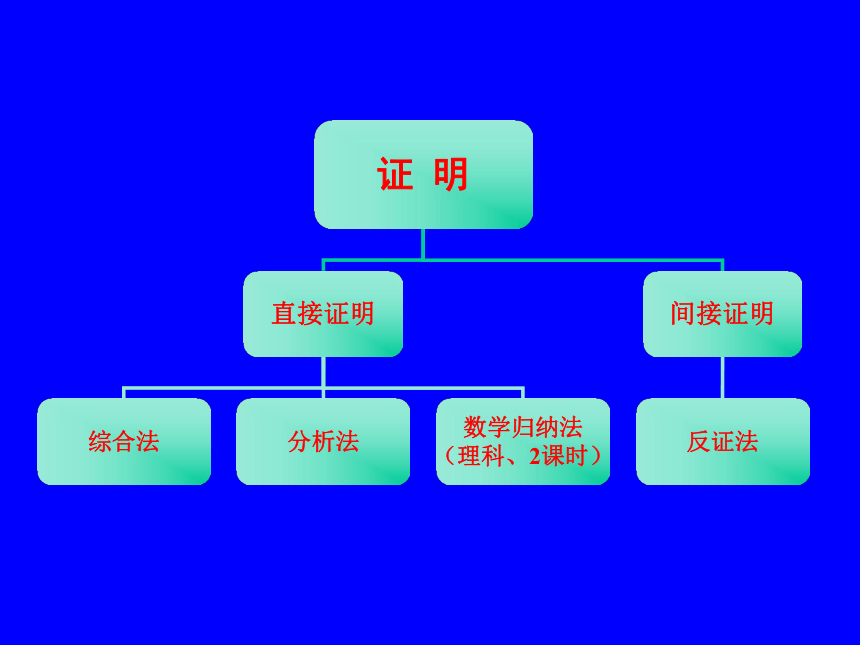
证 明
直接证明
间接证明
综合法
分析法
反证法
数学归纳法
(理科、2课时)
内容与要求
1. 合情推理与演绎推理
⑴ 结合已学过的数学实例和生活中的实例,了解合情推理的含义,能利用归纳和类比等进行简单的推理,体会并认识合情推理在数学发现中的作用.
⑵ 结合已学过的数学实例和生活中的实例,体会演绎推理的重要性,掌握演绎推理的基本方法,并能运用它们进行一些简单推理.
⑶ 通过具体实例,了解合情推理和演绎推理之间的联系和差异.
2. 直接证明与间接证明
⑴ 结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点.
⑵ 结合已经学过的数学实例,了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点.
3. 数学文化
(1)通过对实例的介绍(如欧几里得《几何原本》、马克思《资本论》、杰弗逊《独立宣言》、牛顿三定律),体会公理化思想.
(2)介绍计算机在自动推理领域和数学证明中的作用。
4.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题(仅对理科学生).
二、教学目标
1.了解合情推理和演绎推理的含义。
2.能正确地运用合情推理和演绎推理进行简单的推理。
3.了解合情推理与演绎推理之间的联系与差别。
4.了解直接证明的两种基本方法——分析法和综合法的思考过程、特点。
5.了解间接证明的一种基本方法──反证法的思考过程、特点。
6.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
以学过的知识为载体讲推理和证明方法。
证明方法(除数学归纳法外)是学生在以前的学习中遇到过的,但对它们的特点和内涵不很明确,被动地、不自觉地使用。故本章的主要任务:将推理与证明的方法明确化、显性化,通过具体例子(已学的内容)总结各种证明方法的思考过程和特点、明确它们的内涵,通过应用进行强化,让学生能逐步主动、自觉地使用之。
1. 结合实例了解推理(引入、应用)
紧密结合已学过的数学实例和生活中的实例,以具体的例子为载体,了解合情推理和演绎推理,避免空泛地讲推理。
三、教材特点与教学建议
归纳推理
歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30,
10=3+7,20=3+17,30=13+17.
偶数=奇质数+奇质数
6=3+3,8=3+5,10=5+5,12=5+7,14=7+7,
16=5+11,…, 1 000=29+971,…
⑴ 一个偶数(大于6)总可以表示成两个奇质数之和;
⑵ 没有发现反例 。
歌德巴赫猜想:
任何一个不小于6的偶数都等于两个奇质数之和。
总结特点:
这种由某类事物的部分对象具有某些特征,推出该类事物也具有这些特征的推理,或者由个别事实概括出一般结论的推理,通常称为归纳推理(简称归纳).简言之,归纳推理是由部分到整体、由个别到一般的推理.
归纳推理的一般步骤:
⑴ 对某类事物的部分对象(有限的资料)进行观察、分析、整理;
⑵ 提出猜想;
⑶ 检验猜想!!!
类比推理
“火星上是否有生命”
这种由两类对象具有某些类似特
征,和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比).简言之,类比推理是由特殊到特殊的推理.
总结特点:
类比推理的一般步骤:
⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
⑶ 检验猜想(通过证明确认猜想的正确性,或举出反例否定猜想)!!!
类比推理举例
直角三角形 3个面两两垂直的四面体
∠C=90°
3个边的长度a,b,c
2条直角边a,b和1条斜边c ∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S
类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.
归纳推理、类比推理统称为合情推理.
演绎推理
举例归纳出演绎推理的含义
特点:前提和推理形式(规则)正确,结论正确!
证明函数f(x)=-x2+2x 在(-∞,1)内是增函数.
分析:证明本例所依据的大前提是:在某个区间(a,b)内,如果f’(x)>0,那么函数f(x)在这个区间内单调递增.
小前提是f(x) =-x2+2x 在(-∞,1)内满足f’(x)>0,这是证明本例的关键.
注:很多情况下,省略大前提。
2.纠正典型错误,进一步理解推理
⑴ 合情推理的结论不一定正确
费马猜想:任何形如 (n∈N*)的数都是质数.
反例:
(初步体验证明的必要性)
“平面内,两组对边分别相等的四边形是平行四边形” ;
“平面内,同时垂直于一条直线的两条直线互相平行” .
“空间中,两组对边分别相等的四边形是平
行四边形”;
“空间中,同时垂直于一条直线的两条直线
互相平行”.
类比
⑵ 演绎推理的形式正确,大前提错误,结论也是错误的
3.结合实例讲“证明”
通过熟悉的例子总结各种证明方法的特点、明确它们的内涵,并应用于数学证明,使学生真正作到“论证有据”:
回忆遇到过的某类证明方法的特点
通过证明典型且简单的数学问题或实际问题,体验证明方法的特点
总结特点,给出证明方法的定义
证明的流程框图(提炼特点)
证明数学命题(强化、自觉使用)
综合法
(1)回忆、描述
在数学证明中,我们经常从已知条件和某些学过的定义、定理、公理等出发,通过推理推导出所要的结论.
(2)举例——体验特点
(3)总结特点
一般地,利用已知条件和某些已经学过的定义、公理、定理等,经过一系列的推理、论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法 。
(4)证明数学命题(强化、自觉使用)
分析法
(1)回忆、描述
在数学证明中,我们还经常从要证的结论出发,反推回去,寻求保证结论成立的条件,知道找到一个明显成立的条件为止.
(2)举例、体验特点
(3)总结特点
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
(4)证明数学命题(强化、自觉使用)
反证法
反证法的特点(选修1-2):
选修2-2中的引例稍复杂,解决问题的过程均为:
假设原结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.
应用反证法证明数学命题(强化、自觉使用)
应用反证法的情形:
直接证法难找到证明思路(例题)、需分成很多类进行讨论(引例).
数学归纳法
数学归纳法是一种特殊的证明方法,主要用于证明与正整数有关的数学命题。
特点:通过有限个步骤的推理,证明n取无限多个正整数的情形.
归纳出数学归纳法的原理
一个数学问题(需要探索新的证明方法)
“对于数列{an},已知a1=1,an+1= (n=1,2,…),通过对n = 1,2, 3, 4前4项的归纳,我们已经猜想出其通项公式为 an= .”
逐一验证是不可能的,需要寻求一种方法:通过有限个步骤的推理,证明n取所有正整数都成立.
“多米诺骨牌”全部倒下的原理
使“多米诺骨牌”全部倒下的两个条件:
⑴ 第一块骨牌倒下;
⑵ 任意相邻的两块骨牌,前一块倒下一定导 致后一块倒下.
两个条件的作用:
条件⑴:奠基;条件⑵:递推关系
利用“多米诺骨牌”原理证明这个数学猜想
(经历利用合情推理提出猜想
逻辑推理进行证明)
数学归纳法的原理:
⑴(归纳奠基):命题对n=n0成立(n0为使猜想成立的最小的正整数);
⑵(归纳递推):命题若对n=k成立,则对k+1也成立(k≥n0).
学生普遍存在的问题:
为什么第二步能在假设下进行证明?
第二步实际上是证明一个命题:“假设n=k(k≥n0)时命题成立,证明当n=k+1时命题也成立.”
其本质是证明一个递推关系,归纳递推的作用是从前往后传递.
四、需要注意的问题
1.推理部分的教学重点(发现问题、解决问题)
(1)教学的重点在于通过具体实例理解合情推理与演绎推理,而不追求对概念的抽象表述。
(2)用合情推理探索、猜测结论,并体会证明的必要性
通过实例,引导学生运用合情推理去探索、猜测一些数学结论,并用演绎推理确认所得结论的正确性,或者用反例推翻错误的猜想。(这也是学习和研究的一般方法)
2.根据命题的特点,选择证明方法,并体会证明的必要性
(1)充分重视解决问题的分析过程,引导学生分析命题中条件与结论的特点,选择合适的证明方法。使学生逐步由被动地、不自觉地进行证明,转向主动地、自觉地利用所学方法进行证明。
(2)综合利用各种方法进行证明
在证明一些数学问题时,仅用单一的证明方法很难解决问题,往往需要综合利用各种方法进行证明。例如:
“两头挤”
把分析法和综合法结合起来使用:根据结论的结构特点去转化条件,得到中间结论P;根据条件的结构特点去转化结论,得到中间结论Q.若由P可以推出Q成立,就可以证明结论成立.
3.以已学知识为载体,讲推理、证明方法
例题是以前所学的内容,通过挖掘、提炼、明确其中的推理方法和证明方法,详细分析推理和证明的思路,而不只是表述解题的过程。
4.对证明的技巧性不宜作过高的要求
(讲清楚数学归纳法的原理,但只需用数学归纳法证明一些简单的数学命题。)
5.文理差异
普通高中课程标准实验教科书
(A版)
选修1-2,2-2
推理与证明
一、内容结构
二、教学目标
三、教材特点与教学建议
四、需要注意的问题
一、内容结构
“推理与证明”是数学的基本思维过程,也是人们学习和生活中经常使用的思维方式.推理一般包括合情推理和演绎推理.在本章中,学生将通过对已学知识的回顾,进一步体会合情推理、演绎推理以及二者之间的联系与差异;体会数学证明的特点,了解数学证明的基本方法,包括直接证明的方法(如分析法、综合法、数学归纳法)和间接证明的方法(如反证法);感受逻辑证明在数学以及日常生活中的作用,养成言之有理、论证有据的习惯。
文科(10课时)
2.1合情推理与演绎推理 约5课时
2.2直接证明与间接证明 约4课时
小结 约1课时
理科(8课时)
2.1合情推理与演绎推理 约3课时
2.2直接证明与间接证明 约3课时
2.3数学归纳法 约2课时
推 理
合情推理
(或然性推理)
演绎推理
(必然性推理)
归纳
(部分到整体、
特殊到一般)
类比
(特殊到特殊)
三段论
(一般到特殊)
证 明
直接证明
间接证明
综合法
分析法
反证法
数学归纳法
(理科、2课时)
内容与要求
1. 合情推理与演绎推理
⑴ 结合已学过的数学实例和生活中的实例,了解合情推理的含义,能利用归纳和类比等进行简单的推理,体会并认识合情推理在数学发现中的作用.
⑵ 结合已学过的数学实例和生活中的实例,体会演绎推理的重要性,掌握演绎推理的基本方法,并能运用它们进行一些简单推理.
⑶ 通过具体实例,了解合情推理和演绎推理之间的联系和差异.
2. 直接证明与间接证明
⑴ 结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点.
⑵ 结合已经学过的数学实例,了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点.
3. 数学文化
(1)通过对实例的介绍(如欧几里得《几何原本》、马克思《资本论》、杰弗逊《独立宣言》、牛顿三定律),体会公理化思想.
(2)介绍计算机在自动推理领域和数学证明中的作用。
4.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题(仅对理科学生).
二、教学目标
1.了解合情推理和演绎推理的含义。
2.能正确地运用合情推理和演绎推理进行简单的推理。
3.了解合情推理与演绎推理之间的联系与差别。
4.了解直接证明的两种基本方法——分析法和综合法的思考过程、特点。
5.了解间接证明的一种基本方法──反证法的思考过程、特点。
6.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
以学过的知识为载体讲推理和证明方法。
证明方法(除数学归纳法外)是学生在以前的学习中遇到过的,但对它们的特点和内涵不很明确,被动地、不自觉地使用。故本章的主要任务:将推理与证明的方法明确化、显性化,通过具体例子(已学的内容)总结各种证明方法的思考过程和特点、明确它们的内涵,通过应用进行强化,让学生能逐步主动、自觉地使用之。
1. 结合实例了解推理(引入、应用)
紧密结合已学过的数学实例和生活中的实例,以具体的例子为载体,了解合情推理和演绎推理,避免空泛地讲推理。
三、教材特点与教学建议
归纳推理
歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30,
10=3+7,20=3+17,30=13+17.
偶数=奇质数+奇质数
6=3+3,8=3+5,10=5+5,12=5+7,14=7+7,
16=5+11,…, 1 000=29+971,…
⑴ 一个偶数(大于6)总可以表示成两个奇质数之和;
⑵ 没有发现反例 。
歌德巴赫猜想:
任何一个不小于6的偶数都等于两个奇质数之和。
总结特点:
这种由某类事物的部分对象具有某些特征,推出该类事物也具有这些特征的推理,或者由个别事实概括出一般结论的推理,通常称为归纳推理(简称归纳).简言之,归纳推理是由部分到整体、由个别到一般的推理.
归纳推理的一般步骤:
⑴ 对某类事物的部分对象(有限的资料)进行观察、分析、整理;
⑵ 提出猜想;
⑶ 检验猜想!!!
类比推理
“火星上是否有生命”
这种由两类对象具有某些类似特
征,和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比).简言之,类比推理是由特殊到特殊的推理.
总结特点:
类比推理的一般步骤:
⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
⑶ 检验猜想(通过证明确认猜想的正确性,或举出反例否定猜想)!!!
类比推理举例
直角三角形 3个面两两垂直的四面体
∠C=90°
3个边的长度a,b,c
2条直角边a,b和1条斜边c ∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S
类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.
归纳推理、类比推理统称为合情推理.
演绎推理
举例归纳出演绎推理的含义
特点:前提和推理形式(规则)正确,结论正确!
证明函数f(x)=-x2+2x 在(-∞,1)内是增函数.
分析:证明本例所依据的大前提是:在某个区间(a,b)内,如果f’(x)>0,那么函数f(x)在这个区间内单调递增.
小前提是f(x) =-x2+2x 在(-∞,1)内满足f’(x)>0,这是证明本例的关键.
注:很多情况下,省略大前提。
2.纠正典型错误,进一步理解推理
⑴ 合情推理的结论不一定正确
费马猜想:任何形如 (n∈N*)的数都是质数.
反例:
(初步体验证明的必要性)
“平面内,两组对边分别相等的四边形是平行四边形” ;
“平面内,同时垂直于一条直线的两条直线互相平行” .
“空间中,两组对边分别相等的四边形是平
行四边形”;
“空间中,同时垂直于一条直线的两条直线
互相平行”.
类比
⑵ 演绎推理的形式正确,大前提错误,结论也是错误的
3.结合实例讲“证明”
通过熟悉的例子总结各种证明方法的特点、明确它们的内涵,并应用于数学证明,使学生真正作到“论证有据”:
回忆遇到过的某类证明方法的特点
通过证明典型且简单的数学问题或实际问题,体验证明方法的特点
总结特点,给出证明方法的定义
证明的流程框图(提炼特点)
证明数学命题(强化、自觉使用)
综合法
(1)回忆、描述
在数学证明中,我们经常从已知条件和某些学过的定义、定理、公理等出发,通过推理推导出所要的结论.
(2)举例——体验特点
(3)总结特点
一般地,利用已知条件和某些已经学过的定义、公理、定理等,经过一系列的推理、论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法 。
(4)证明数学命题(强化、自觉使用)
分析法
(1)回忆、描述
在数学证明中,我们还经常从要证的结论出发,反推回去,寻求保证结论成立的条件,知道找到一个明显成立的条件为止.
(2)举例、体验特点
(3)总结特点
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
(4)证明数学命题(强化、自觉使用)
反证法
反证法的特点(选修1-2):
选修2-2中的引例稍复杂,解决问题的过程均为:
假设原结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.
应用反证法证明数学命题(强化、自觉使用)
应用反证法的情形:
直接证法难找到证明思路(例题)、需分成很多类进行讨论(引例).
数学归纳法
数学归纳法是一种特殊的证明方法,主要用于证明与正整数有关的数学命题。
特点:通过有限个步骤的推理,证明n取无限多个正整数的情形.
归纳出数学归纳法的原理
一个数学问题(需要探索新的证明方法)
“对于数列{an},已知a1=1,an+1= (n=1,2,…),通过对n = 1,2, 3, 4前4项的归纳,我们已经猜想出其通项公式为 an= .”
逐一验证是不可能的,需要寻求一种方法:通过有限个步骤的推理,证明n取所有正整数都成立.
“多米诺骨牌”全部倒下的原理
使“多米诺骨牌”全部倒下的两个条件:
⑴ 第一块骨牌倒下;
⑵ 任意相邻的两块骨牌,前一块倒下一定导 致后一块倒下.
两个条件的作用:
条件⑴:奠基;条件⑵:递推关系
利用“多米诺骨牌”原理证明这个数学猜想
(经历利用合情推理提出猜想
逻辑推理进行证明)
数学归纳法的原理:
⑴(归纳奠基):命题对n=n0成立(n0为使猜想成立的最小的正整数);
⑵(归纳递推):命题若对n=k成立,则对k+1也成立(k≥n0).
学生普遍存在的问题:
为什么第二步能在假设下进行证明?
第二步实际上是证明一个命题:“假设n=k(k≥n0)时命题成立,证明当n=k+1时命题也成立.”
其本质是证明一个递推关系,归纳递推的作用是从前往后传递.
四、需要注意的问题
1.推理部分的教学重点(发现问题、解决问题)
(1)教学的重点在于通过具体实例理解合情推理与演绎推理,而不追求对概念的抽象表述。
(2)用合情推理探索、猜测结论,并体会证明的必要性
通过实例,引导学生运用合情推理去探索、猜测一些数学结论,并用演绎推理确认所得结论的正确性,或者用反例推翻错误的猜想。(这也是学习和研究的一般方法)
2.根据命题的特点,选择证明方法,并体会证明的必要性
(1)充分重视解决问题的分析过程,引导学生分析命题中条件与结论的特点,选择合适的证明方法。使学生逐步由被动地、不自觉地进行证明,转向主动地、自觉地利用所学方法进行证明。
(2)综合利用各种方法进行证明
在证明一些数学问题时,仅用单一的证明方法很难解决问题,往往需要综合利用各种方法进行证明。例如:
“两头挤”
把分析法和综合法结合起来使用:根据结论的结构特点去转化条件,得到中间结论P;根据条件的结构特点去转化结论,得到中间结论Q.若由P可以推出Q成立,就可以证明结论成立.
3.以已学知识为载体,讲推理、证明方法
例题是以前所学的内容,通过挖掘、提炼、明确其中的推理方法和证明方法,详细分析推理和证明的思路,而不只是表述解题的过程。
4.对证明的技巧性不宜作过高的要求
(讲清楚数学归纳法的原理,但只需用数学归纳法证明一些简单的数学命题。)
5.文理差异
