4.3.1 角
图片预览
文档简介
(共20张PPT)
今日的课题:
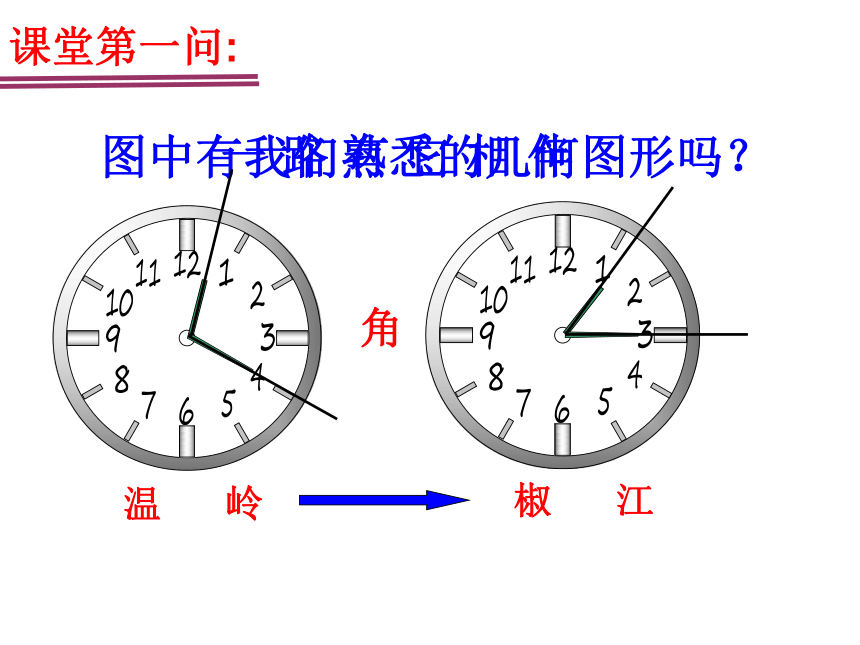
课堂第一问:
温 岭
椒 江
图中有我们熟悉的几何图形吗?
一 路 有 它 相 伴
角
课堂第一问:
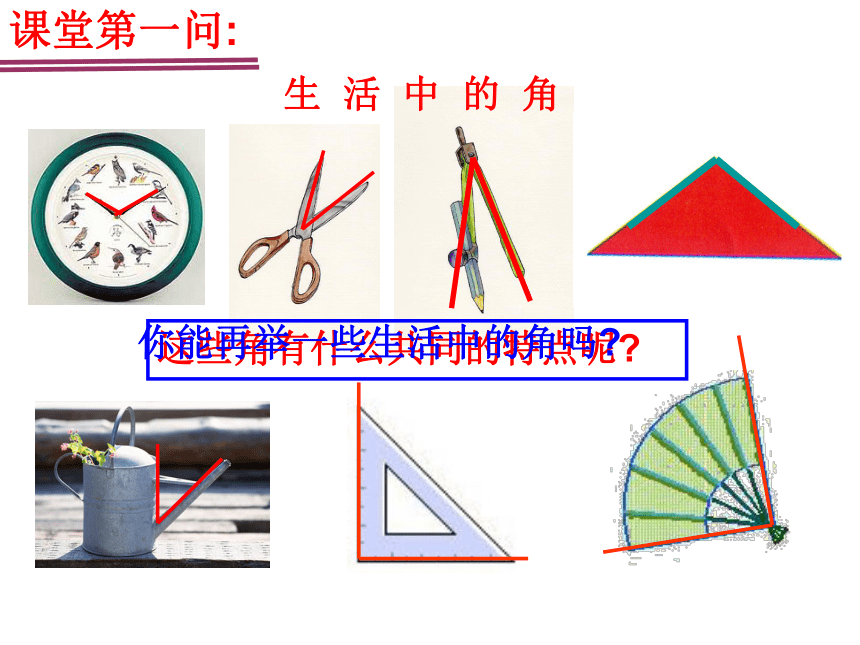
这些角有什么共同的特点呢
生 活 中 的 角
你能再举一些生活中的角吗
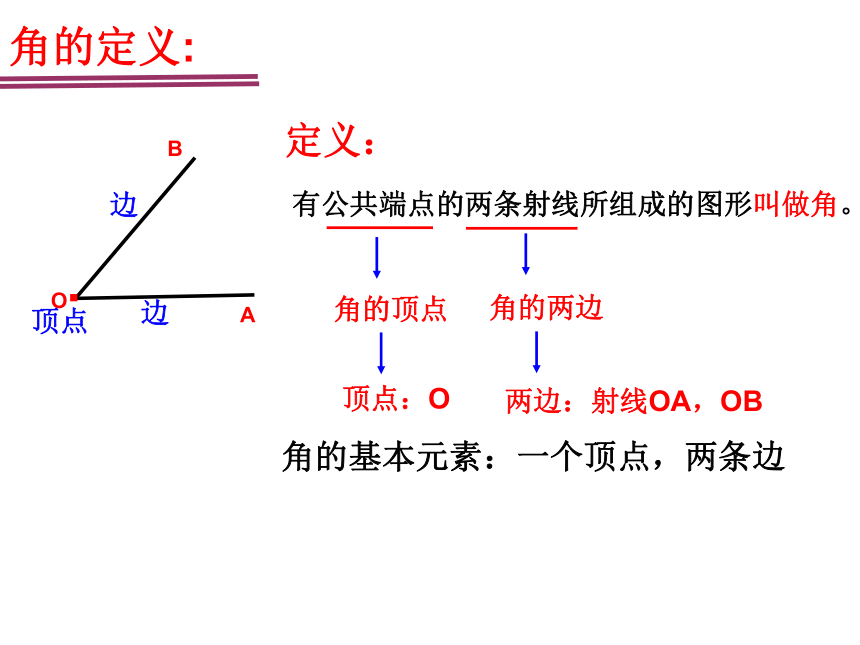
有公共端点的两条射线所组成的图形叫做角。
角的定义:
定义:
角的顶点
角的两边
·
O
A
B
顶点:O
两边:射线OA,OB
角的基本元素:一个顶点,两条边
顶点
边
边
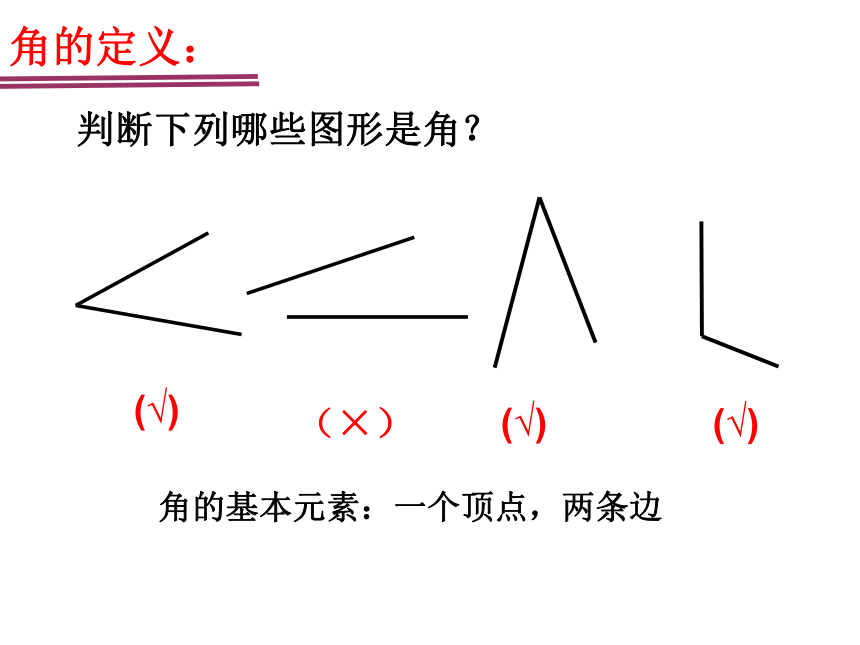
判断下列哪些图形是角?
(√)
(√)
(√)
(×)
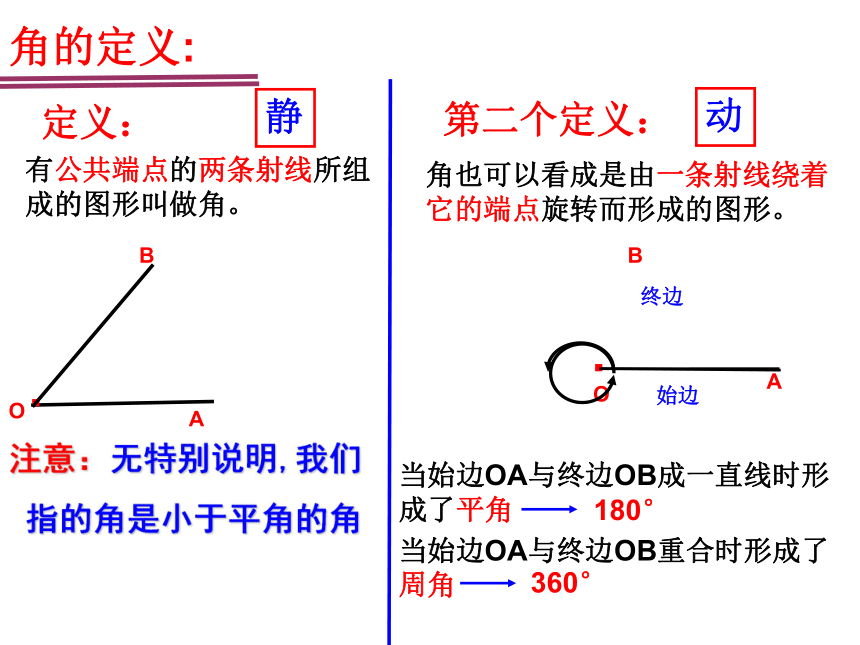
角的定义:
角的基本元素:一个顶点,两条边
角也可以看成是由一条射线绕着它的端点旋转而形成的图形。
角的定义:
有公共端点的两条射线所组成的图形叫做角。
定义:
O
·
A
B
·
A
O
B
第二个定义:
始边
终边
当始边OA与终边OB成一直线时形成了平角
180°
当始边OA与终边OB重合时形成了周角
360°
注意:无特别说明,我们
指的角是小于平角的角
静
动
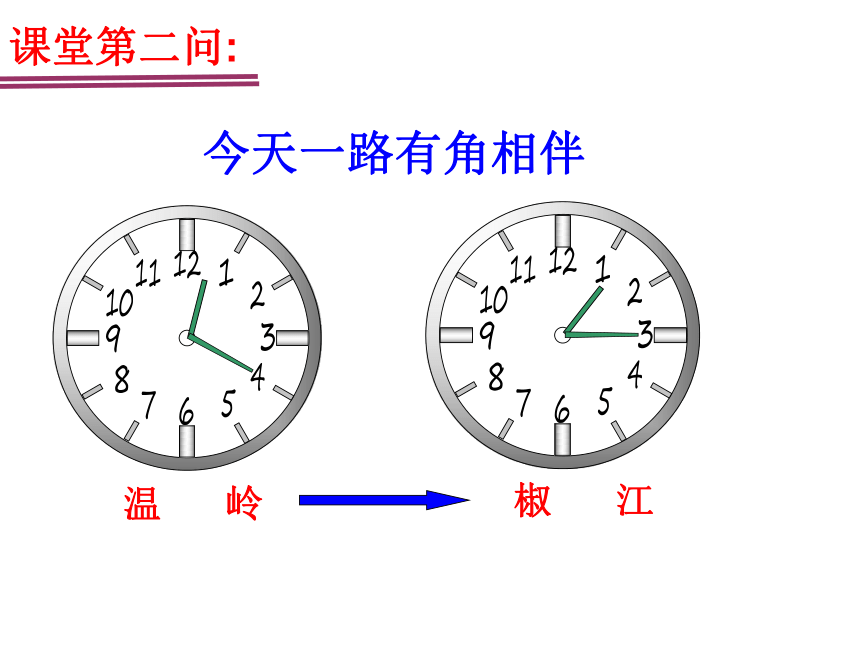
课堂第二问:
温 岭
椒 江
今天一路有角相伴
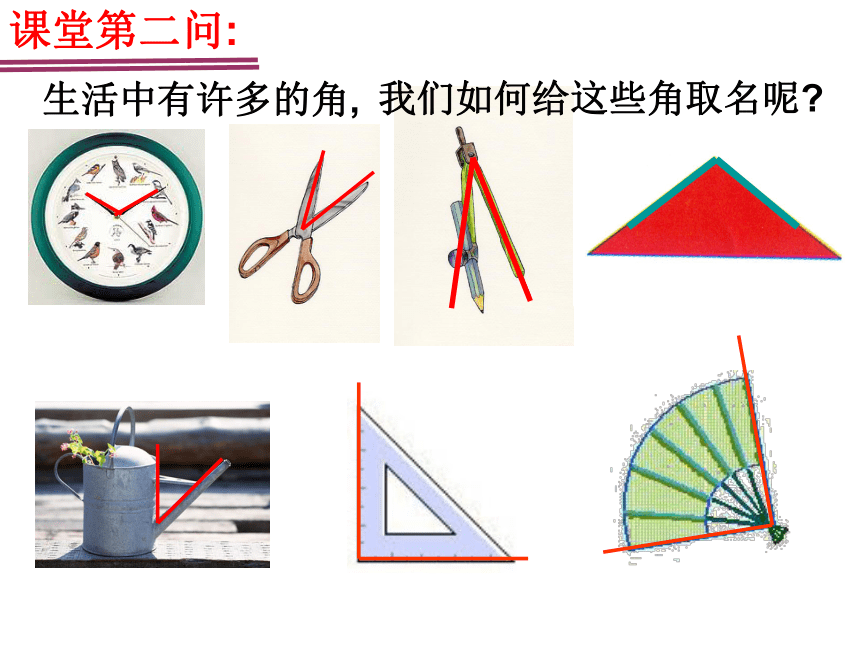
生活中有许多的角,
课堂第二问:
我们如何给这些角取名呢
O
A
B
α
1
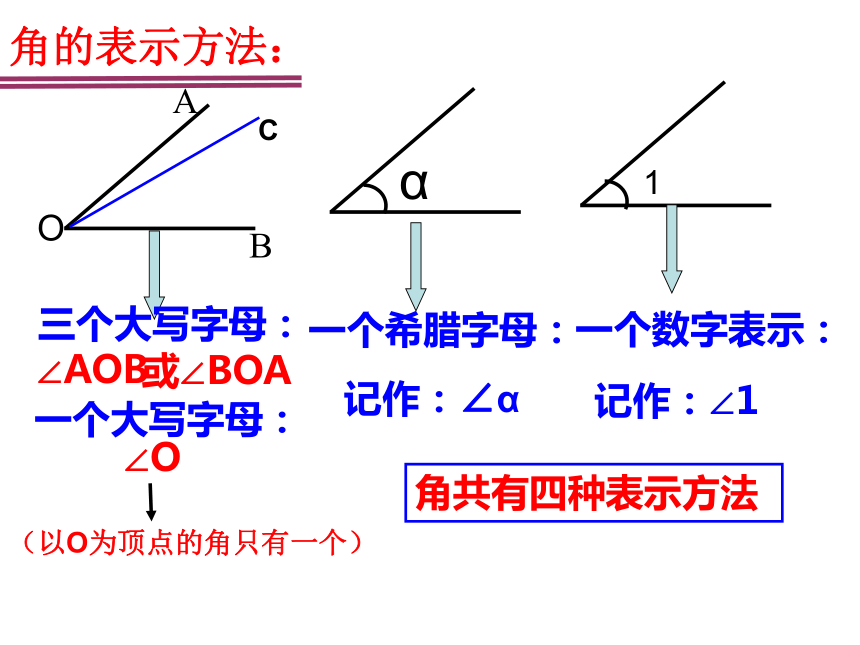
三个大写字母:
记作:∠α
一个数字表示:
角的表示方法:
或∠BOA
∠O
(以O为顶点的角只有一个)
一个大写字母:
∠AOB
一个希腊字母:
记作:∠1
C
角共有四种表示方法
(a) ∠1就是∠A;
A
B
D
C
M
1
2
3
(b) ∠2就是∠B;
(c) ∠3就是∠C .
1.判断下面说法对不对:
课堂第二问:
∠ABC
A
C
B
D
E
1
2
2.将图中的角用不同的方法表示出来,并填写下表:
∠BAD
∠2
∠ α
∠B
角的表示方法:
课堂第二问:
O
A
B
C
3.图中有几个角呢?
用适当的方式表示这些角:
3个
∠AOB
∠AOC
∠BOC
∠O
×
O
A
B
C
D
E
F
思考:
(1)以D为顶点的角有哪几个:
1
∠EDC
∠EDO
∠CDF
∠ODF
∠1
(2)图中共有几个角?
15
1
2
∠2
∠1
课堂第三问:
温 岭
椒 江
从温岭到椒江,一路有角相伴
(时间变了,角度也变了)
∠APB与∠COD大小如何呢?
C
D
O
B
A
P
P
课堂第三问:
角的基本度量单位:
度、分、秒
分、秒的定义:
把 的角等分成60份,
①
②
把 的角等分成60份,
即:
角的度量工具:
量角器
类比
时间单位
每一份就是1分,记作
每一份就是1秒,记作
(60进制)
例:5°= ′= ″;
38°15′= °
36″= ′= °
38.15°= ° ′;
角的度量:
1周角
1平角
1直角
角的基本度量单位:
度、分、秒
1周角
300
18000
38
9
0.6
0.01
38.25
=360°
=180°
=90 °
=2平角
=4直角
度 分秒
不足1度的化成分
不足1分的化成秒
分秒
度
秒
分
度
1.用度、分、秒表示:
⑴0.75°= ′= ″
⑵1.2 ′ = °
⑶16.24°= ° ′ ″
45
2700
0.02
16
14
24
0.15 =0.15
如果两个角一个为18.15 ,一个为18 15',它们一样大吗
单位要统一
角的度量:
解:∵ 18.15 =18 +0.15
∴18.15 = 18 9 '
∴ 18.15 ≠18 15'
60'
=9'
18 15'
=18 +0.15 '
0.15 ' =
0.15×
=0.025°
∴ 18 15' = 18.025
∴ 18.15 ≠18 15'
畅所欲言:
我的收获……
生活中的角
角的两种定义
角的四种表示方法
角的度、分、秒
单位间的换算
(静和动)
(顶点要写在中间)
(一个字母表示如∠B)
(60进制)
生活中的实际问题
数学问题
观察,探究
抽象,概括
角度制起源于四大文明古国之一的古代巴比伦.为什么选择60这个数作为进制的基数呢 据说是由于60这个数是许多常用的数2,3,4,5,6,10,12,15,20,30倍数, 60=12 ×5,12是一年中的月数,5是一只手的手指数,所以古巴比伦人认为60是一个特别而又重要的数.
角的小知识:
度量角的单位:
角度制
弧度制
密位制
测量角的仪器:
量角器
经纬仪
借用三角尺找特殊角
课堂第四问:
温 岭
椒 江
你能帮忙算出温岭出发和到达椒江两个时刻时针与分针的夹角吗
今日的课题:
课堂第一问:
温 岭
椒 江
图中有我们熟悉的几何图形吗?
一 路 有 它 相 伴
角
课堂第一问:
这些角有什么共同的特点呢
生 活 中 的 角
你能再举一些生活中的角吗
有公共端点的两条射线所组成的图形叫做角。
角的定义:
定义:
角的顶点
角的两边
·
O
A
B
顶点:O
两边:射线OA,OB
角的基本元素:一个顶点,两条边
顶点
边
边
判断下列哪些图形是角?
(√)
(√)
(√)
(×)
角的定义:
角的基本元素:一个顶点,两条边
角也可以看成是由一条射线绕着它的端点旋转而形成的图形。
角的定义:
有公共端点的两条射线所组成的图形叫做角。
定义:
O
·
A
B
·
A
O
B
第二个定义:
始边
终边
当始边OA与终边OB成一直线时形成了平角
180°
当始边OA与终边OB重合时形成了周角
360°
注意:无特别说明,我们
指的角是小于平角的角
静
动
课堂第二问:
温 岭
椒 江
今天一路有角相伴
生活中有许多的角,
课堂第二问:
我们如何给这些角取名呢
O
A
B
α
1
三个大写字母:
记作:∠α
一个数字表示:
角的表示方法:
或∠BOA
∠O
(以O为顶点的角只有一个)
一个大写字母:
∠AOB
一个希腊字母:
记作:∠1
C
角共有四种表示方法
(a) ∠1就是∠A;
A
B
D
C
M
1
2
3
(b) ∠2就是∠B;
(c) ∠3就是∠C .
1.判断下面说法对不对:
课堂第二问:
∠ABC
A
C
B
D
E
1
2
2.将图中的角用不同的方法表示出来,并填写下表:
∠BAD
∠2
∠ α
∠B
角的表示方法:
课堂第二问:
O
A
B
C
3.图中有几个角呢?
用适当的方式表示这些角:
3个
∠AOB
∠AOC
∠BOC
∠O
×
O
A
B
C
D
E
F
思考:
(1)以D为顶点的角有哪几个:
1
∠EDC
∠EDO
∠CDF
∠ODF
∠1
(2)图中共有几个角?
15
1
2
∠2
∠1
课堂第三问:
温 岭
椒 江
从温岭到椒江,一路有角相伴
(时间变了,角度也变了)
∠APB与∠COD大小如何呢?
C
D
O
B
A
P
P
课堂第三问:
角的基本度量单位:
度、分、秒
分、秒的定义:
把 的角等分成60份,
①
②
把 的角等分成60份,
即:
角的度量工具:
量角器
类比
时间单位
每一份就是1分,记作
每一份就是1秒,记作
(60进制)
例:5°= ′= ″;
38°15′= °
36″= ′= °
38.15°= ° ′;
角的度量:
1周角
1平角
1直角
角的基本度量单位:
度、分、秒
1周角
300
18000
38
9
0.6
0.01
38.25
=360°
=180°
=90 °
=2平角
=4直角
度 分秒
不足1度的化成分
不足1分的化成秒
分秒
度
秒
分
度
1.用度、分、秒表示:
⑴0.75°= ′= ″
⑵1.2 ′ = °
⑶16.24°= ° ′ ″
45
2700
0.02
16
14
24
0.15 =0.15
如果两个角一个为18.15 ,一个为18 15',它们一样大吗
单位要统一
角的度量:
解:∵ 18.15 =18 +0.15
∴18.15 = 18 9 '
∴ 18.15 ≠18 15'
60'
=9'
18 15'
=18 +0.15 '
0.15 ' =
0.15×
=0.025°
∴ 18 15' = 18.025
∴ 18.15 ≠18 15'
畅所欲言:
我的收获……
生活中的角
角的两种定义
角的四种表示方法
角的度、分、秒
单位间的换算
(静和动)
(顶点要写在中间)
(一个字母表示如∠B)
(60进制)
生活中的实际问题
数学问题
观察,探究
抽象,概括
角度制起源于四大文明古国之一的古代巴比伦.为什么选择60这个数作为进制的基数呢 据说是由于60这个数是许多常用的数2,3,4,5,6,10,12,15,20,30倍数, 60=12 ×5,12是一年中的月数,5是一只手的手指数,所以古巴比伦人认为60是一个特别而又重要的数.
角的小知识:
度量角的单位:
角度制
弧度制
密位制
测量角的仪器:
量角器
经纬仪
借用三角尺找特殊角
课堂第四问:
温 岭
椒 江
你能帮忙算出温岭出发和到达椒江两个时刻时针与分针的夹角吗
