12.1轴对称
图片预览




文档简介
(共19张PPT)
12.1 轴对称
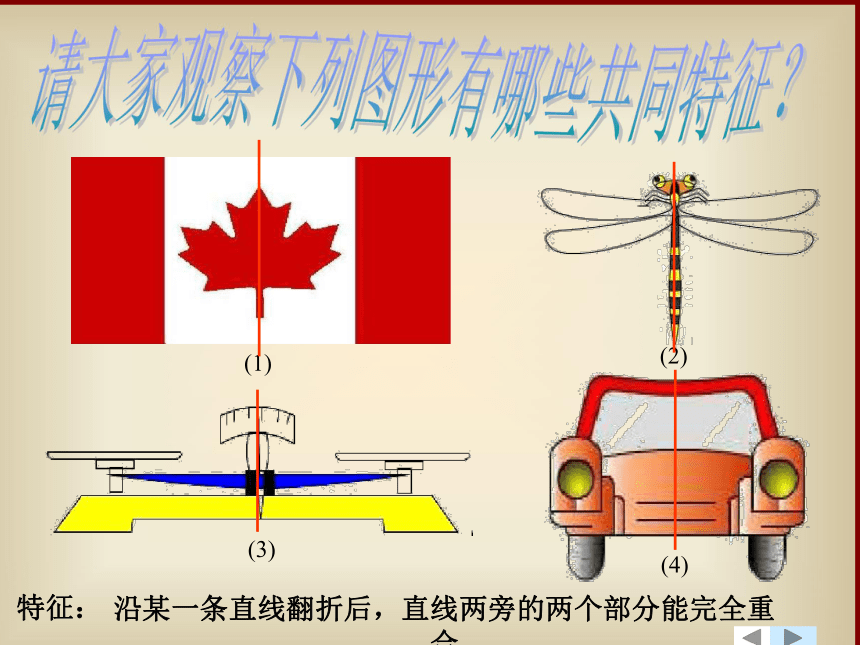
沿某一条直线翻折后,直线两旁的两个部分能完全重合
(1)
(2)
(3)
(4)
特征:
1. 把一个图形沿着某一条直线翻折,如果直线两旁的部分能够互相重合,这个图形就是轴对称图形
2. 这条直线是这个图形的对称轴
一、 轴对称图形和对称轴的定义:
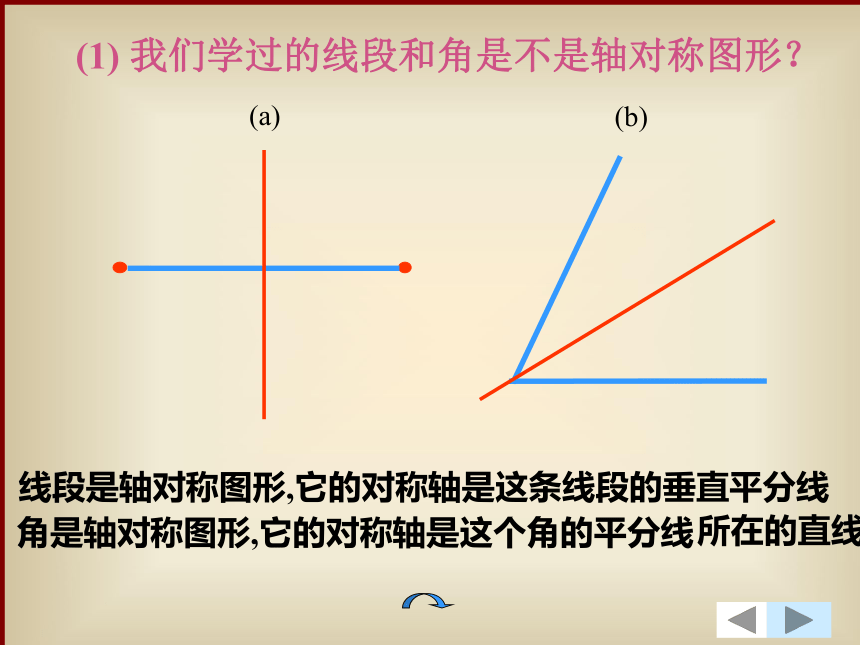
(1) 我们学过的线段和角是不是轴对称图形?
(a)
(b)
线段是轴对称图形,它的对称轴是这条线段的垂直平分线
角是轴对称图形,它的对称轴是这个角的平分线
所在的直线
请大家想一想平行 四边行是否为轴对称图形?
平行四边形不是轴对称图形!
正方形
矩形
等边 三角形
菱形
圆
等腰梯形
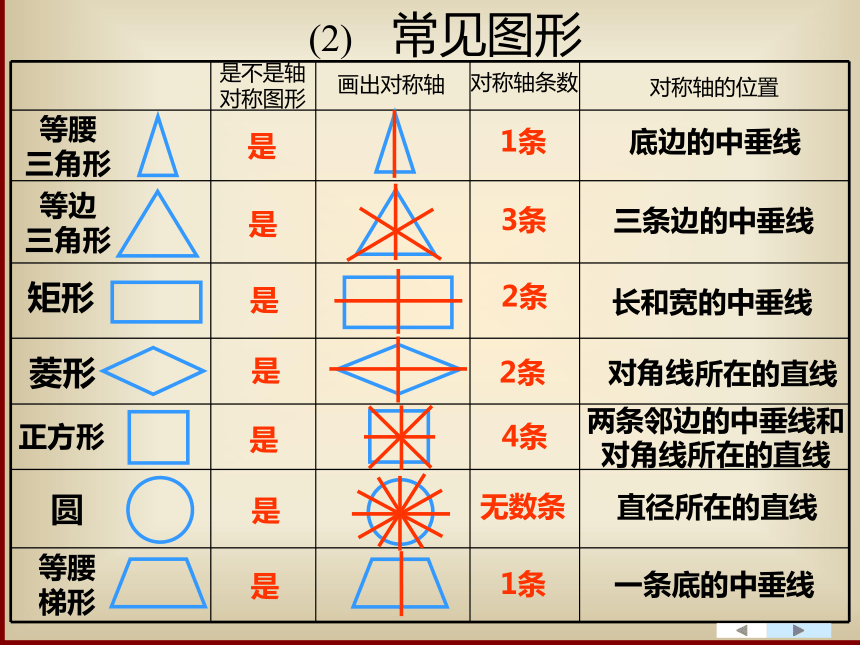
对称轴条数
3条
4条
2条
1条
无数条
2条
(2) 常见图形
对称轴的位置
长和宽的中垂线
两条邻边的中垂线和对角线所在的直线
三条边的中垂线
对角线
直径所在的直线
一条底的中垂线
所在的直线
等腰 三角形
画出对称轴
1条
底边的中垂线
是不是轴对称图形
是
是
是
是
是
是
是
下列(1) (2)两个图形有什么区别?
(1)
(2)
轴对称
轴对称图形
两个图形
一个图形
1. 平面上的两个图形,将其中一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称, 简称轴对称,这条直线叫对称轴
二、轴对称和对称点的定义:
注意:
2. 两个图形中的对应点(即两图形重合时互相重合的点)叫做关于这条直线的对称点
它本身
如果一点在对称轴上,它的对称点就是
1. △ABC和△A’ B ’ C ’是否关于直线l对称?为什么?
2. 线段AB与线段A ’ B ’否关于直线l对称?为什么? BC与B ’ C ’ ,CA与C ’ A ’呢?
3. 点A和B ’点关于直线l的对称点各是哪一点?
△ABC△ A ’ B ’ C ’关于直线l对称。
点A和点A ’,点B和点B ’ ,点C ’和点C ’分别是关于直线l的对称点
“轴对称图形”是指同一个图形的两部分 沿某直线翻折时,两部分重合的图形。
“轴对称”是指两个图形分别位于某条直 线的两侧,且沿这条直线翻折时,两个 图形重合 。
区别:
(1) 定义中都有一条对称轴,都要沿着这 条直线折叠重合
(2) 如果把成轴对称的两个图形看成一个 整体,那么这个整体的图形就是轴对 称图形; 如果把一个轴对称图形沿着对称轴分 成的两部分看成两个图形,那么这两 个图形是轴对称的
联系:
轴对称图形
两个图形成轴对称
区别
联
系
一个图形
两个图形
1、沿着直线某条直线折叠后,直线两旁的部分能互相重合
2、都有对称轴(至少一条)
3、如果把一个轴对称图形沿对称轴分成两 个图形,那么这两个图形关于这条直线对称;反之,如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形。
练习:
一、判断
轴对称图形必有对称轴 ( )
轴对称图形至少有一条对称轴 ( )
关于某直线成轴对称的两个图形必能互相重合( )
两个完全互相重合的图形必是轴对称( )
1. 符合下列哪个条件的图形是轴对称图形? ( )
(A)能够互相重合的两个图形
(B)一个图形在某直线翻折,能与另一个图形重合
(C)一个图形在某直线两旁部分的形状大小都相同
(D)一个图形沿某直线翻折,直线两旁的部分能够 互相重合
二、选择
D
小结:
1.本节课你学到了什么
2.你掌握了什么数学方法
欣赏:生活中的轴对称
北大校门
欣赏:生活中的轴对称
清华校门
欣赏:生活中的轴对称
斯里兰卡
1. B册 P44
2. 一课一练
P65 一、填空题
二、选择题
12.1 轴对称
沿某一条直线翻折后,直线两旁的两个部分能完全重合
(1)
(2)
(3)
(4)
特征:
1. 把一个图形沿着某一条直线翻折,如果直线两旁的部分能够互相重合,这个图形就是轴对称图形
2. 这条直线是这个图形的对称轴
一、 轴对称图形和对称轴的定义:
(1) 我们学过的线段和角是不是轴对称图形?
(a)
(b)
线段是轴对称图形,它的对称轴是这条线段的垂直平分线
角是轴对称图形,它的对称轴是这个角的平分线
所在的直线
请大家想一想平行 四边行是否为轴对称图形?
平行四边形不是轴对称图形!
正方形
矩形
等边 三角形
菱形
圆
等腰梯形
对称轴条数
3条
4条
2条
1条
无数条
2条
(2) 常见图形
对称轴的位置
长和宽的中垂线
两条邻边的中垂线和对角线所在的直线
三条边的中垂线
对角线
直径所在的直线
一条底的中垂线
所在的直线
等腰 三角形
画出对称轴
1条
底边的中垂线
是不是轴对称图形
是
是
是
是
是
是
是
下列(1) (2)两个图形有什么区别?
(1)
(2)
轴对称
轴对称图形
两个图形
一个图形
1. 平面上的两个图形,将其中一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称, 简称轴对称,这条直线叫对称轴
二、轴对称和对称点的定义:
注意:
2. 两个图形中的对应点(即两图形重合时互相重合的点)叫做关于这条直线的对称点
它本身
如果一点在对称轴上,它的对称点就是
1. △ABC和△A’ B ’ C ’是否关于直线l对称?为什么?
2. 线段AB与线段A ’ B ’否关于直线l对称?为什么? BC与B ’ C ’ ,CA与C ’ A ’呢?
3. 点A和B ’点关于直线l的对称点各是哪一点?
△ABC△ A ’ B ’ C ’关于直线l对称。
点A和点A ’,点B和点B ’ ,点C ’和点C ’分别是关于直线l的对称点
“轴对称图形”是指同一个图形的两部分 沿某直线翻折时,两部分重合的图形。
“轴对称”是指两个图形分别位于某条直 线的两侧,且沿这条直线翻折时,两个 图形重合 。
区别:
(1) 定义中都有一条对称轴,都要沿着这 条直线折叠重合
(2) 如果把成轴对称的两个图形看成一个 整体,那么这个整体的图形就是轴对 称图形; 如果把一个轴对称图形沿着对称轴分 成的两部分看成两个图形,那么这两 个图形是轴对称的
联系:
轴对称图形
两个图形成轴对称
区别
联
系
一个图形
两个图形
1、沿着直线某条直线折叠后,直线两旁的部分能互相重合
2、都有对称轴(至少一条)
3、如果把一个轴对称图形沿对称轴分成两 个图形,那么这两个图形关于这条直线对称;反之,如果把两个成轴对称的图形看成一个图形,那么这个图形就是轴对称图形。
练习:
一、判断
轴对称图形必有对称轴 ( )
轴对称图形至少有一条对称轴 ( )
关于某直线成轴对称的两个图形必能互相重合( )
两个完全互相重合的图形必是轴对称( )
1. 符合下列哪个条件的图形是轴对称图形? ( )
(A)能够互相重合的两个图形
(B)一个图形在某直线翻折,能与另一个图形重合
(C)一个图形在某直线两旁部分的形状大小都相同
(D)一个图形沿某直线翻折,直线两旁的部分能够 互相重合
二、选择
D
小结:
1.本节课你学到了什么
2.你掌握了什么数学方法
欣赏:生活中的轴对称
北大校门
欣赏:生活中的轴对称
清华校门
欣赏:生活中的轴对称
斯里兰卡
1. B册 P44
2. 一课一练
P65 一、填空题
二、选择题
