2021-2022学年人教版八年级上册数学12.3 角的平分线的性质(第2课时)课件(共17张)
文档属性
| 名称 | 2021-2022学年人教版八年级上册数学12.3 角的平分线的性质(第2课时)课件(共17张) | 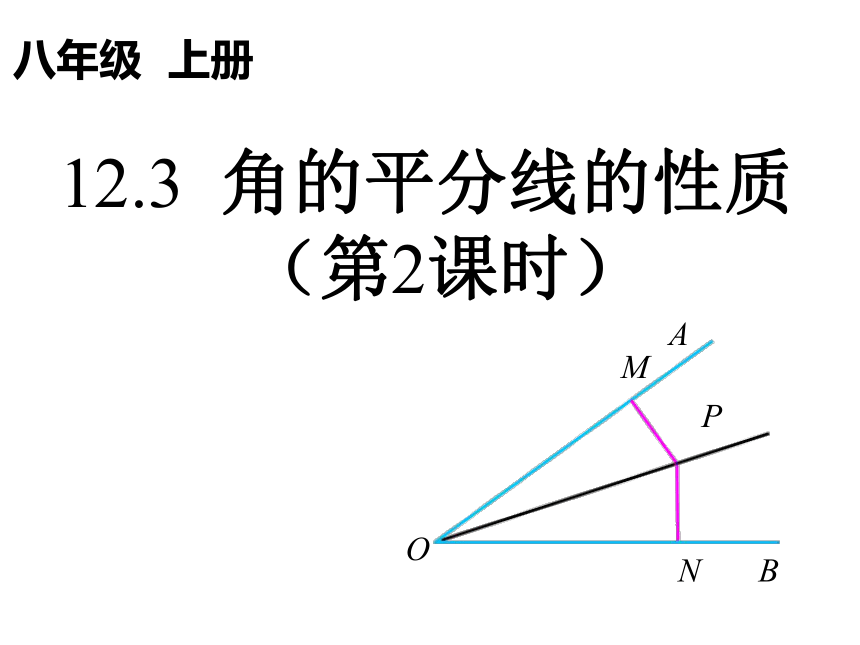 | |
| 格式 | zip | ||
| 文件大小 | 467.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-23 20:53:09 | ||
图片预览



文档简介
(共17张PPT)
八年级 上册
12.3 角的平分线的性质 (第2课时)
A
B
O
P
M
N
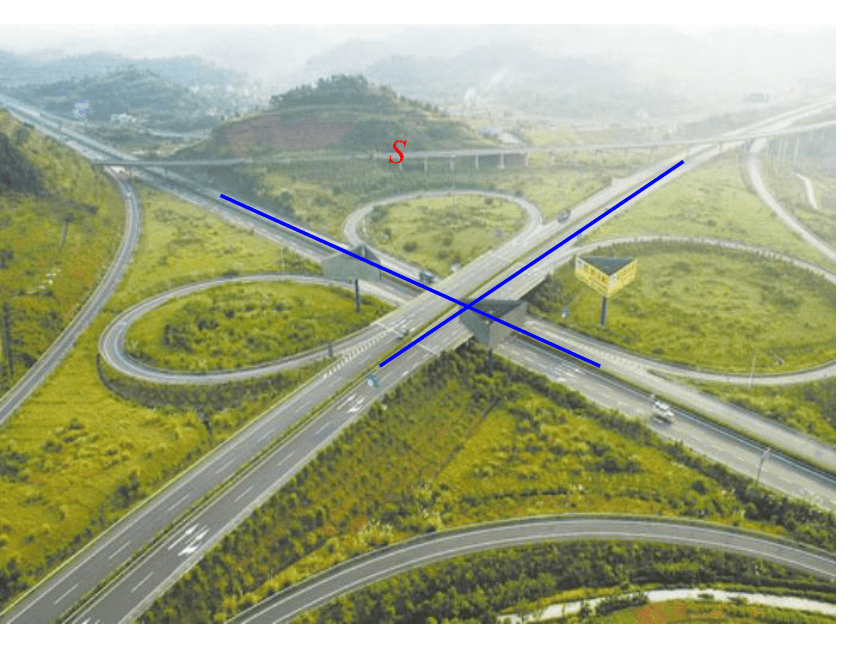
问题1 如图,要在S 区建一个广告牌P,使它到
两条高速公路的距离相等,离两条公路交叉处500 m,
请你帮忙设计一下,这个广告牌P 应建于何处(在图上
标出它的位置,比例尺为1:20 000)?
S
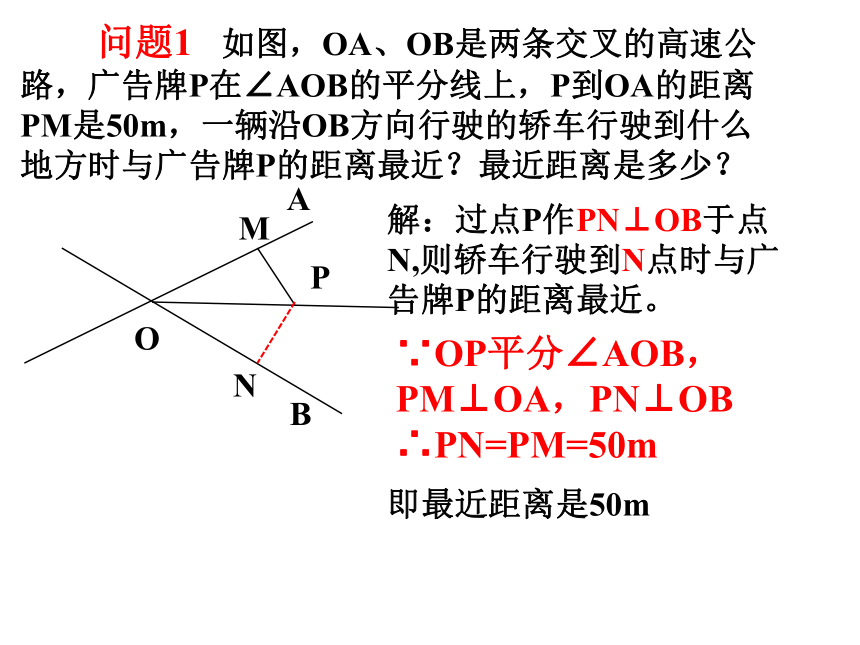
问题1 如图,OA、OB是两条交叉的高速公路,广告牌P在∠AOB的平分线上,P到OA的距离PM是50m,一辆沿OB方向行驶的轿车行驶到什么地方时与广告牌P的距离最近?最近距离是多少?
O
A
B
P
M
N
解:过点P作PN⊥OB于点N,则轿车行驶到N点时与广告牌P的距离最近。
∵OP平分∠AOB, PM⊥OA,PN⊥OB
∴PN=PM=50m
即最近距离是50m
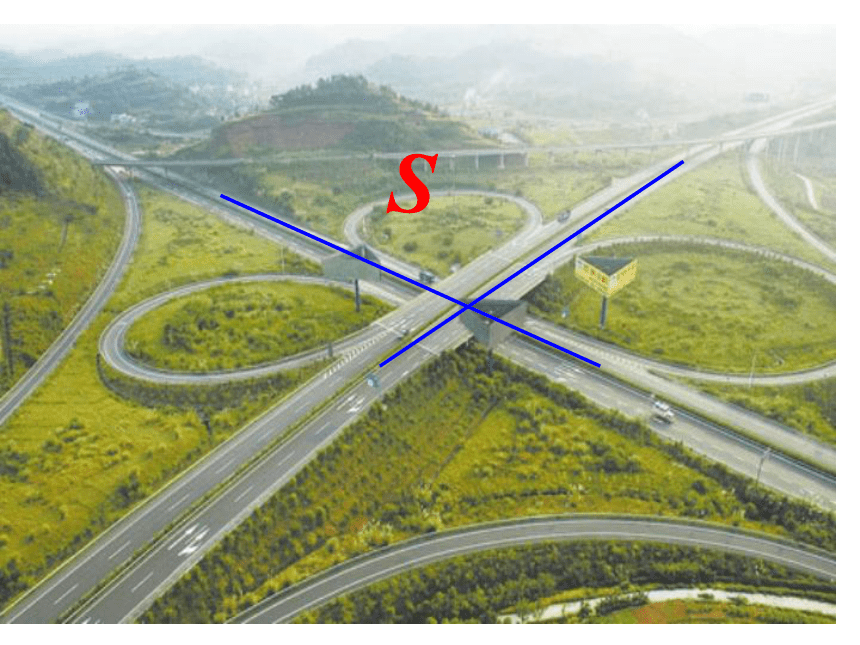
问题1 如图,要在S 区建一个广告牌P,使它到
两条高速公路的距离相等,离两条公路交叉处500 m,
请你帮忙设计一下,这个广告牌P 应建于何处(在图上
标出它的位置,比例尺为1:20 000)?
S
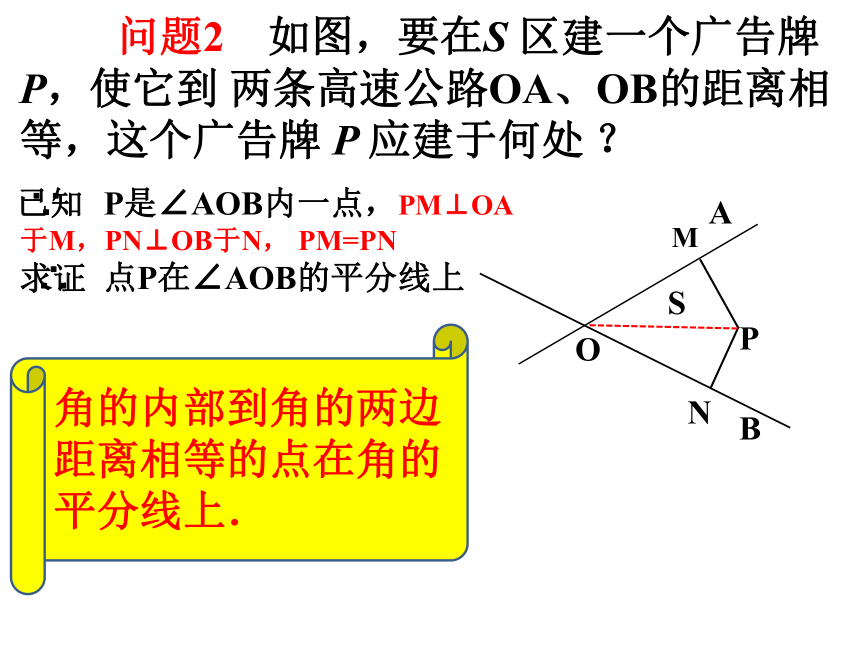
问题2 如图,要在S 区建一个广告牌P,使它到 两条高速公路OA、OB的距离相等,这个广告牌 P 应建于何处 ?
O
A
B
S
角的内部到角的两边距离相等的点在角的平分线上.
P
M
N
P是∠AOB内一点,PM⊥OA于M,PN⊥OB于N, PM=PN
点P在∠AOB的平分线上
∵
∴
已知
求证
证明:连接OP
∵PM⊥OA PN⊥OB
∴∠PMO=∠PNO=90°
在Rt△PMO和Rt△PNO中
{
∴ Rt△PMO≌Rt△PNO
∴∠MOP=∠NOP
即点P在∠AOB的平分线上
PM=PN
OP=OP
X
A
B
O
Q
M
N
1.判断题:
(1)如图,若QM =QN,则OQ 平分∠AOB;( )
(2)如图,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线; ( )
(3)已知:Q 到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )
×
√
在问题2中,在S 区建一个广告牌P,使它到两
条公路OA、OB的距离相等.
(1) 这样的广告牌可建多少个?
探究
(2) 若这个广告牌P 离两条公路交叉处500 m(在图上标出它的位置,比例尺为1:20 000),这个广告牌 应建于何处?
O
A
B
S
(3).有一条和两条公路OA、OB都相交的铁路AB,
要在S 区建一个广告牌P,使它到三条路的距离都
相等.这个广告牌P 应建在 何处?
已知∠OAB、∠OBA的平分线相交于点P.
求证:点P在∠AOB的平分线上
O
A
B
S
P
M
N
H
(4) 如图,将问题3中“S 区”去掉,广告牌P
到两条公路和一条铁路的距离相等.这个广告牌P 应建
在何处?
公路
公路
铁路
P1
P2
P3
P4
1 本节课我学到的知识有:?
2 我独立自学 能力( ) A 强 B 一般 C 差
3 我小组合作学习( ) A 积极 B 一般 C 不积极
3 我展示交流( ) A 积极 B 一般 C 不积极
4我听讲( ) A 认真 B 一般 C 不认真
自我评价:
说明:总结出一个知识点记1分,选项A记2 分,选项B 记1分,选项C记0分.满分10分。
总得分 分
快乐源于探索
特别感谢你们的合作!
检测题
如图,点P在∠AOB的平分线上,PE⊥OA于
E,PF⊥OB于F,若PE等于3,则PF= ( )
2. 如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点,OE⊥AC于E,OE=2,则AB与CD之间的距离为 ( )
A
B
O
P
E
F
A
B
C
D
O
E
3. 如图,OP平分∠ MON, PA⊥ ON于A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
A. 1 B. 2 C. 3 D. 4
4. 如图,△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若AC=3,AB=7,则BE的长为( )
3 B. 3.5 C. 4 D.不能确定
A
O
P
M
N
Q
A
B
C
D
E
5. 如图,BD=CD,BF⊥AC于F,CE⊥AB于E. 求证:点D在∠BAC的平分线上.
A
B
C
D
E
F
教科书习题12.3第3、7题.
布置作业
性质 判定
图形
已知
结论
用途
A
B
O
P
M
N
OP是∠AOB的平分线
PM⊥OA , PN⊥OB
PM⊥OA,PN⊥OB, PM=PN
PM=PN
OP是∠AOB的平分线
证明线段相等
证明角相等
角的平分线的性质与判定的区别
文字
语言
角的平分线上的点到角两边的距离相等
角的内部到角两边距离相等的点在角的平分线上
八年级 上册
12.3 角的平分线的性质 (第2课时)
A
B
O
P
M
N
问题1 如图,要在S 区建一个广告牌P,使它到
两条高速公路的距离相等,离两条公路交叉处500 m,
请你帮忙设计一下,这个广告牌P 应建于何处(在图上
标出它的位置,比例尺为1:20 000)?
S
问题1 如图,OA、OB是两条交叉的高速公路,广告牌P在∠AOB的平分线上,P到OA的距离PM是50m,一辆沿OB方向行驶的轿车行驶到什么地方时与广告牌P的距离最近?最近距离是多少?
O
A
B
P
M
N
解:过点P作PN⊥OB于点N,则轿车行驶到N点时与广告牌P的距离最近。
∵OP平分∠AOB, PM⊥OA,PN⊥OB
∴PN=PM=50m
即最近距离是50m
问题1 如图,要在S 区建一个广告牌P,使它到
两条高速公路的距离相等,离两条公路交叉处500 m,
请你帮忙设计一下,这个广告牌P 应建于何处(在图上
标出它的位置,比例尺为1:20 000)?
S
问题2 如图,要在S 区建一个广告牌P,使它到 两条高速公路OA、OB的距离相等,这个广告牌 P 应建于何处 ?
O
A
B
S
角的内部到角的两边距离相等的点在角的平分线上.
P
M
N
P是∠AOB内一点,PM⊥OA于M,PN⊥OB于N, PM=PN
点P在∠AOB的平分线上
∵
∴
已知
求证
证明:连接OP
∵PM⊥OA PN⊥OB
∴∠PMO=∠PNO=90°
在Rt△PMO和Rt△PNO中
{
∴ Rt△PMO≌Rt△PNO
∴∠MOP=∠NOP
即点P在∠AOB的平分线上
PM=PN
OP=OP
X
A
B
O
Q
M
N
1.判断题:
(1)如图,若QM =QN,则OQ 平分∠AOB;( )
(2)如图,若QM⊥OA 于M,QN⊥OB 于N,则OQ是∠AOB 的平分线; ( )
(3)已知:Q 到OA 的距离等于2 cm, 且Q 到OB 距离等于2 cm,则Q 在∠AOB 的平分线上.( )
×
√
在问题2中,在S 区建一个广告牌P,使它到两
条公路OA、OB的距离相等.
(1) 这样的广告牌可建多少个?
探究
(2) 若这个广告牌P 离两条公路交叉处500 m(在图上标出它的位置,比例尺为1:20 000),这个广告牌 应建于何处?
O
A
B
S
(3).有一条和两条公路OA、OB都相交的铁路AB,
要在S 区建一个广告牌P,使它到三条路的距离都
相等.这个广告牌P 应建在 何处?
已知∠OAB、∠OBA的平分线相交于点P.
求证:点P在∠AOB的平分线上
O
A
B
S
P
M
N
H
(4) 如图,将问题3中“S 区”去掉,广告牌P
到两条公路和一条铁路的距离相等.这个广告牌P 应建
在何处?
公路
公路
铁路
P1
P2
P3
P4
1 本节课我学到的知识有:?
2 我独立自学 能力( ) A 强 B 一般 C 差
3 我小组合作学习( ) A 积极 B 一般 C 不积极
3 我展示交流( ) A 积极 B 一般 C 不积极
4我听讲( ) A 认真 B 一般 C 不认真
自我评价:
说明:总结出一个知识点记1分,选项A记2 分,选项B 记1分,选项C记0分.满分10分。
总得分 分
快乐源于探索
特别感谢你们的合作!
检测题
如图,点P在∠AOB的平分线上,PE⊥OA于
E,PF⊥OB于F,若PE等于3,则PF= ( )
2. 如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点,OE⊥AC于E,OE=2,则AB与CD之间的距离为 ( )
A
B
O
P
E
F
A
B
C
D
O
E
3. 如图,OP平分∠ MON, PA⊥ ON于A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
A. 1 B. 2 C. 3 D. 4
4. 如图,△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,若AC=3,AB=7,则BE的长为( )
3 B. 3.5 C. 4 D.不能确定
A
O
P
M
N
Q
A
B
C
D
E
5. 如图,BD=CD,BF⊥AC于F,CE⊥AB于E. 求证:点D在∠BAC的平分线上.
A
B
C
D
E
F
教科书习题12.3第3、7题.
布置作业
性质 判定
图形
已知
结论
用途
A
B
O
P
M
N
OP是∠AOB的平分线
PM⊥OA , PN⊥OB
PM⊥OA,PN⊥OB, PM=PN
PM=PN
OP是∠AOB的平分线
证明线段相等
证明角相等
角的平分线的性质与判定的区别
文字
语言
角的平分线上的点到角两边的距离相等
角的内部到角两边距离相等的点在角的平分线上
