人教新课标A版必修1第三章 函数的应用 单元练习(含答案)
文档属性
| 名称 | 人教新课标A版必修1第三章 函数的应用 单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 97.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 14:56:31 | ||
图片预览




文档简介
人教新课标必修一第三章
函数的应用
一、单选题
1.(2021高一上·桂林月考)已知12是函数 的一个零点,则 的值是( )
A. 1 B. 0 C. 2 D. +1
2.(2021高三上·洮南月考)已知函数f(x)= (a∈R),若函数f(x)在R上有两个零点,则实数a的取值范围是( )
A. (0,1] B. [1,+∞) C. (0,1) D. (-∞,1]
3.(2020高一上·芜湖期末)某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )
A. 13立方米 B. 14立方米 C. 18立方米 D. 26立方米
4.(2019高二上·南宁月考)设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)- g(x)在x∈[a,b]上有两个不同的解,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为( ).
A. B. C. D.
5.(2019高三上·霍邱月考)下列函数中,既是偶函数又存在零点的是( )
A. B. C. D.
6.(2020高一上·贵州期末)已知函数 有一个零点所在的区间为 ,则 可能等于( )
A. 0 B. 1 C. 2 D. 3
7.(2019高一下·鄂尔多斯期中)函数 的图象与函数 的图象的交点个数是( )
A. 2 B. 3 C. 4 D. 5
8.(2020高三上·南开期末)已知 ,若函数 有三个或者四个零点,则函数 的零点个数为( )
A. 1或2 B. 2 C. 1或0 D. 0或1或2
9.(2020·海拉尔模拟)已知 ,若方程 有唯一解,则实数a的取值范围是( )
A. B.
C. D.
10.(2020高二下·武汉期中)已知曲线 与曲线 有三个交点,则实数 的取值范围为( )
A. B. C. D.
二、填空题
11.(2020高一上·佛山期末)依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起我国正式执行新个税法,个税的部分税率级距进一步优化调整,扩大3%、10%、20%三档低税率的级距,减税向中低收入人群倾斜.税率与速算扣除数见下表:
级数 全年应纳税所得额所在区间 税率(%) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 1692
4 (300000,420000] 25 3192
5 (420000,660000] 30 N
小华的全年应纳税所得额为100000元,则全年应缴个税为 元.还有一种速算个税的办法:全年应纳税所得额
×对应档的税率-对应档的速算扣除数,即小华全年应缴个税为 元.按照这一算法,当小李的全年应纳税所得额为200000元时,全年应缴个税为 , 表中的N= .
12.(2019高一上·屯溪期中)若函数 存在零点,则m的取值范围是________.
13.(2020高三上·安徽月考)已知函数 ,则函数 的零点个数是________.
14.(2019高一上·上饶期中)设 ,若 恰有3个不相等的实数根,则实数 的取值范围是 .
15.(2020高一上·黄陵期中)用二分法求方程 在区间 上零点的近似值,先取区间中点 ,则下一个含根的区间是 .
16.(2019·新宁模拟)设 ,则g(g(-1))=________.
17.(2020高一上·宁波期末)已知函数 ,若 在区间 内没有零点,则 的取值范围是________.
18.(2018高三上·酉阳期末)定义域为 的偶函数 满足对 ,有 ,且当 时, ,若函数 在 上至多有三个零点,则 的取值范围是 .
三、解答题
19.(2019高一上·东方月考)设函数f(x)=
(1)若f(a)=1,求a的值
(2)解不等式:
20.(2020高一上·浦东期末)某商品销售价格和销售量与销售天数有关,第 天 的销售价格 (元 百斤),第 天 的销售量 (百斤)(销售收入 销售价格 销售量)
(1)求第10天销售该商品的销售收入是多少
(2)这20天中,哪一天的销售收入最大 最大值为多少
21.(2020高一下·上海期中)2019年10月1日为庆祝中国人民共和国成立70周年在北京天安门广场举行了盛大的阅兵仪式,共有580台(套)装备、160余架各型飞机接受检阅,受阅装备均为中国国产现役主战装备,其中包括部分首次公开亮相的新型装备.例如,在无人作战第三方队中就包括了两型侦察干扰无人机,可以在遥控设备或自备程序控制操纵的情况下执行任务,进行对敌方通讯设施的电磁压制和干扰,甚至压制敌人的防空系统.某作战部门对某处的战场实施“电磁干扰”实验,据测定,该处的“干扰指数”与无人机干扰源的强度和距离之比成正比,比例系数为常数 ( ),现已知相距36 的 、 两处配置两架无人机干扰源,其对敌干扰的强度分别为1和 ( ),它们连线段上任意一点 处的干扰指数 等于两机对该处的干扰指数之和,设 ( ).
(1)试将 表示为 的函数,指出其定义域;
(2)当 , 时,试确定“干扰指数”最小时 所处位置.
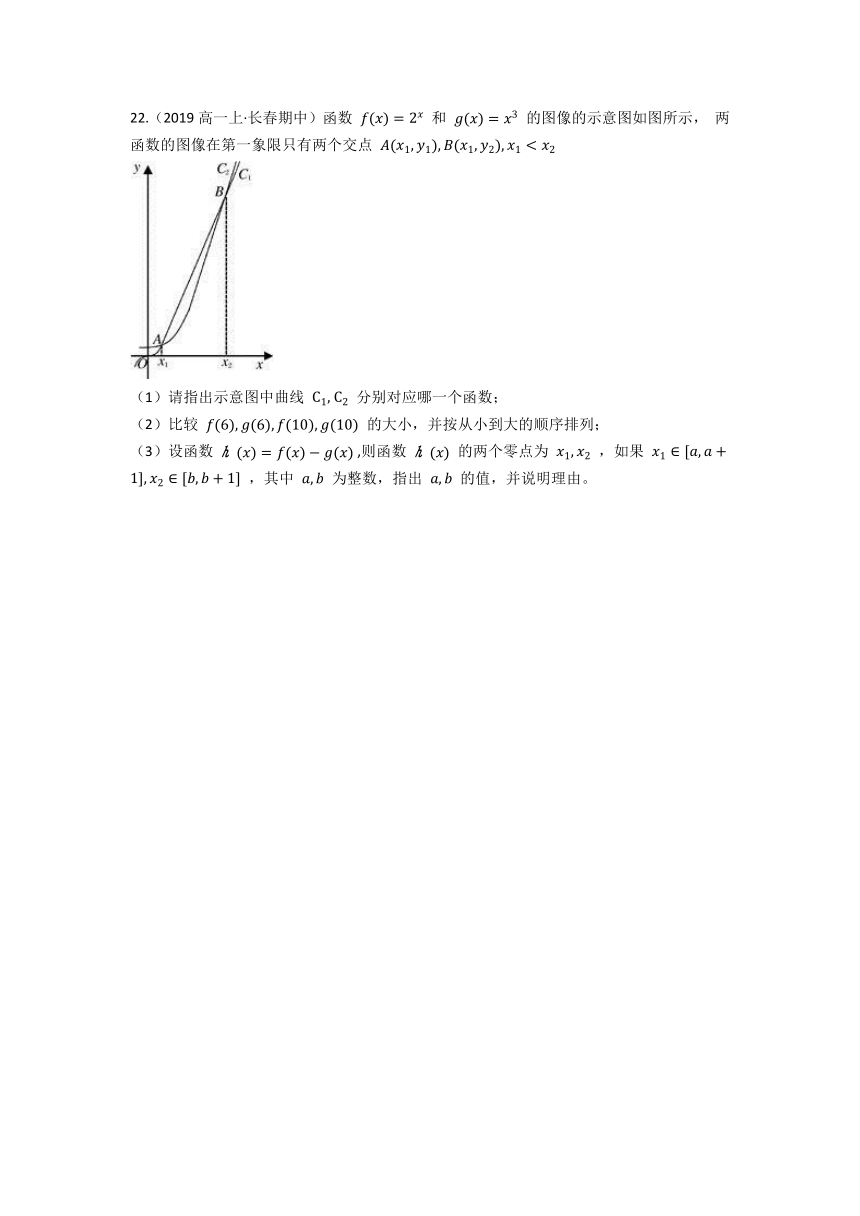
22.(2019高一上·长春期中)函数 和 的图像的示意图如图所示, 两函数的图像在第一象限只有两个交点
(1)请指出示意图中曲线 分别对应哪一个函数;
(2)比较 的大小,并按从小到大的顺序排列;
(3)设函数 ,则函数 的两个零点为 ,如果 ,其中 为整数,指出 的值,并说明理由。
答案解析部分
一、单选题
1.【答案】 B
【解析】由题意知: ,可得 ,
∴ ,则 .
∴ .
故答案为:B
2.【答案】 A
【解析】解:当 x≤0时,f(x)单调递增,∴f(x)≤f(0)=1-a;
当 x>0时,f(x)单调递增,且f(x)>-a,
∵f(x)在R上有两个零点,
∴ , 解得 0故答案为:A
3.【答案】 A
【解析】设职工的用水量为 立方米,需要交纳的水费为 元,
当 时, ,
当 时, ,
即函数的解析式为: ,
据此分类讨论:
当 时, ,解得 ,不合题意,舍去;
当 时, ,解得 ,符合题意;
综上可得:该职工这个月实际用水为13立方米.
故答案为:A.
4.【答案】 A
【解析】∵ 与 在 上是“关联函数”
∴函数 在 上有两个不同零点
∴ ,解得 .
故答案为:A.
5.【答案】 D
【解析】对于A,定义域为R,为偶函数,没有零点;
对于B,sin(﹣x)=﹣sinx,是奇函数,由无数个零点;
对于C,定义域为(0,+∞),所以是非奇非偶的函数,有一个零点;
对于D,定义域为R,并且cos(﹣x)=cosx,是偶函数并且有无数个零点;
故答案为:D.
6.【答案】 B
【解析】因为 , , , ,
所以 ,且函数的图象连续不断,
所以函数 有一个零点所在的区间为 ,故 可能等于1.
故答案为:B
7.【答案】 B
【解析】依题意,画出两个函数的图像如下图所示,
由图可知,两个函数图像有 个交点,
故答案为:B.
8.【答案】 A
【解析】当 时, ,由 , 得 ,当 时, ,由 得 ,所以当 时函数 有三个零点或四个零点,对 ,由 得 ,当 时, 有一个零点;由于 ,所以 有一个零点或两个零点,
故答案为:A.
9.【答案】 B
【解析】解:令 ,则 ,
则 ,
故 ,如图示:
由 ,
得 ,
函数 恒过 , ,
由 , ,
可得 , , ,
若方程 有唯一解,
则 或 ,即 或 ;
当 即图象相切时,
根据 , ,
解得 舍去),
则 的范围是 ,
故答案为:B.
10.【答案】 C
【解析】已知曲线 与曲线 有三个交点,等价于方程 有三个不等的实根,即方程 有三个不等的实根,
令 ,则 ,显然当 时, ,函数 单调递增,且此时 的值域为 ;当 时, ,函数 单调递减,且此时 的值域为 ,
故函数 的最大值为 ,
又因为方程 有三个不等的实根,等价于方程 有两个不等的实根,且一个大于0小于 ,一个小于0,
故可得 ,解得 。
故答案为:C
二、填空题
11.【答案】 23080;52920
【解析】根据全年应纳税所得额×对应档的税率-对应档的速算扣除数,
可得小李的全年应纳税所得额为200000元时,应缴个税为
(元),
当全年应纳税所得额为500000元时,即全年应缴个税为
,
解得 (元).
故答案为:23080;52920
12.【答案】
【解析】解:设 ,因为 ,所以函数函数 存在零点时,则满足m的取值范围是-1 m<0,故答案为
13.【答案】 7
【解析】当 时,
当 时,
当 时,
函数 的实数根的个数; 即方程 的实数根的个数.
在同一坐标系中作出 与 的图象,
由 ,如图,函数 的图象与 的图象有7个交点.
所以函数 的零点个数是:7
故答案为:7
14.【答案】
【解析】 的图象如图: , 是二次函数的一部分, 时取得最大值4, , 是指数函数的一部分的图象, 时, ,由题意可知 .
故答案为: .
15.【答案】
【解析】 在 上单调递增, , , ,因为 ,则 ,所以 ,则 ,所以下一个含根区间应该为 .
故答案为:
16.【答案】 -1
【解析】解:根据题意,则。
故答案为:-1
17.【答案】
【解析】
,
由 ,可得 ,解得 , ,
因为 在区间 内没有零点,
所以 ,且 ,
即 且 ,
因为 ,
分别取 ,1,2,3 ,
,
,
∴ 的取值范围是 ,
故答案为: 。
18.【答案】
【解析】
∵f(x+2)=f(x)﹣f(1),
且f(x)是定义域为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
又f(﹣1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2 ,
函数的图象为开口向下、顶点为(3,0)的抛物线.
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至多有3个交点.
可以分两种情况:其一是有交点时,其二是一个交点也没有,
当一个交点都没有时,即a>1.
当有交点时,∵f(x)≤0,∴g(x)≤0,可得0<a<1,
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至多有三个零点,
则有g(4)即loga5<﹣2,∴5> ,解得,又0<a<1,∴ <a<1,
故答案为: 。
三、解答题
19.【答案】 (1)解: 且 ,
当 时, 解得 ;
当 时, 解得 ;
综上可得 或
(2)解:
①当 时,由 在其定义域上单调递增,
解得 ,即
②当 时,由 在其定义域上单调递减,
解得 ,即
20.【答案】 (1)解:当 时, , ,
因此,第10天销售该商品的销售收入是 ;
(2)解:设 .
①当 且 时, ,
,
此时,函数 单调递减, ;
②当 且 时, ,
,
此时,函数 单调递减, .
,因此,这 天中,第一天的销售收入最大,且销售收入的最大值为 元.
21.【答案】 (1)解:根据题意,点C受A干扰指数为 ,点C受B干扰指数为 ,
所以点C处干扰指数为: .
(2)解:因为 ,
所以 ,
当且仅当 ,即 时,取等号,
所以“干扰指数”最小时 所处位置在距A点6公里处.
22.【答案】 (1)解:C1对应的函数为 ,C2对应的函数为 .
(2)解:
所以从小到大依次为
(3)解:计算得
理由如下:
令 ,
由于 ,
则函数 的两个零点
因此整数
函数的应用
一、单选题
1.(2021高一上·桂林月考)已知12是函数 的一个零点,则 的值是( )
A. 1 B. 0 C. 2 D. +1
2.(2021高三上·洮南月考)已知函数f(x)= (a∈R),若函数f(x)在R上有两个零点,则实数a的取值范围是( )
A. (0,1] B. [1,+∞) C. (0,1) D. (-∞,1]
3.(2020高一上·芜湖期末)某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )
A. 13立方米 B. 14立方米 C. 18立方米 D. 26立方米
4.(2019高二上·南宁月考)设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)- g(x)在x∈[a,b]上有两个不同的解,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为( ).
A. B. C. D.
5.(2019高三上·霍邱月考)下列函数中,既是偶函数又存在零点的是( )
A. B. C. D.
6.(2020高一上·贵州期末)已知函数 有一个零点所在的区间为 ,则 可能等于( )
A. 0 B. 1 C. 2 D. 3
7.(2019高一下·鄂尔多斯期中)函数 的图象与函数 的图象的交点个数是( )
A. 2 B. 3 C. 4 D. 5
8.(2020高三上·南开期末)已知 ,若函数 有三个或者四个零点,则函数 的零点个数为( )
A. 1或2 B. 2 C. 1或0 D. 0或1或2
9.(2020·海拉尔模拟)已知 ,若方程 有唯一解,则实数a的取值范围是( )
A. B.
C. D.
10.(2020高二下·武汉期中)已知曲线 与曲线 有三个交点,则实数 的取值范围为( )
A. B. C. D.
二、填空题
11.(2020高一上·佛山期末)依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起我国正式执行新个税法,个税的部分税率级距进一步优化调整,扩大3%、10%、20%三档低税率的级距,减税向中低收入人群倾斜.税率与速算扣除数见下表:
级数 全年应纳税所得额所在区间 税率(%) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 1692
4 (300000,420000] 25 3192
5 (420000,660000] 30 N
小华的全年应纳税所得额为100000元,则全年应缴个税为 元.还有一种速算个税的办法:全年应纳税所得额
×对应档的税率-对应档的速算扣除数,即小华全年应缴个税为 元.按照这一算法,当小李的全年应纳税所得额为200000元时,全年应缴个税为 , 表中的N= .
12.(2019高一上·屯溪期中)若函数 存在零点,则m的取值范围是________.
13.(2020高三上·安徽月考)已知函数 ,则函数 的零点个数是________.
14.(2019高一上·上饶期中)设 ,若 恰有3个不相等的实数根,则实数 的取值范围是 .
15.(2020高一上·黄陵期中)用二分法求方程 在区间 上零点的近似值,先取区间中点 ,则下一个含根的区间是 .
16.(2019·新宁模拟)设 ,则g(g(-1))=________.
17.(2020高一上·宁波期末)已知函数 ,若 在区间 内没有零点,则 的取值范围是________.
18.(2018高三上·酉阳期末)定义域为 的偶函数 满足对 ,有 ,且当 时, ,若函数 在 上至多有三个零点,则 的取值范围是 .
三、解答题
19.(2019高一上·东方月考)设函数f(x)=
(1)若f(a)=1,求a的值
(2)解不等式:
20.(2020高一上·浦东期末)某商品销售价格和销售量与销售天数有关,第 天 的销售价格 (元 百斤),第 天 的销售量 (百斤)(销售收入 销售价格 销售量)
(1)求第10天销售该商品的销售收入是多少
(2)这20天中,哪一天的销售收入最大 最大值为多少
21.(2020高一下·上海期中)2019年10月1日为庆祝中国人民共和国成立70周年在北京天安门广场举行了盛大的阅兵仪式,共有580台(套)装备、160余架各型飞机接受检阅,受阅装备均为中国国产现役主战装备,其中包括部分首次公开亮相的新型装备.例如,在无人作战第三方队中就包括了两型侦察干扰无人机,可以在遥控设备或自备程序控制操纵的情况下执行任务,进行对敌方通讯设施的电磁压制和干扰,甚至压制敌人的防空系统.某作战部门对某处的战场实施“电磁干扰”实验,据测定,该处的“干扰指数”与无人机干扰源的强度和距离之比成正比,比例系数为常数 ( ),现已知相距36 的 、 两处配置两架无人机干扰源,其对敌干扰的强度分别为1和 ( ),它们连线段上任意一点 处的干扰指数 等于两机对该处的干扰指数之和,设 ( ).
(1)试将 表示为 的函数,指出其定义域;
(2)当 , 时,试确定“干扰指数”最小时 所处位置.
22.(2019高一上·长春期中)函数 和 的图像的示意图如图所示, 两函数的图像在第一象限只有两个交点
(1)请指出示意图中曲线 分别对应哪一个函数;
(2)比较 的大小,并按从小到大的顺序排列;
(3)设函数 ,则函数 的两个零点为 ,如果 ,其中 为整数,指出 的值,并说明理由。
答案解析部分
一、单选题
1.【答案】 B
【解析】由题意知: ,可得 ,
∴ ,则 .
∴ .
故答案为:B
2.【答案】 A
【解析】解:当 x≤0时,f(x)单调递增,∴f(x)≤f(0)=1-a;
当 x>0时,f(x)单调递增,且f(x)>-a,
∵f(x)在R上有两个零点,
∴ , 解得 0
3.【答案】 A
【解析】设职工的用水量为 立方米,需要交纳的水费为 元,
当 时, ,
当 时, ,
即函数的解析式为: ,
据此分类讨论:
当 时, ,解得 ,不合题意,舍去;
当 时, ,解得 ,符合题意;
综上可得:该职工这个月实际用水为13立方米.
故答案为:A.
4.【答案】 A
【解析】∵ 与 在 上是“关联函数”
∴函数 在 上有两个不同零点
∴ ,解得 .
故答案为:A.
5.【答案】 D
【解析】对于A,定义域为R,为偶函数,没有零点;
对于B,sin(﹣x)=﹣sinx,是奇函数,由无数个零点;
对于C,定义域为(0,+∞),所以是非奇非偶的函数,有一个零点;
对于D,定义域为R,并且cos(﹣x)=cosx,是偶函数并且有无数个零点;
故答案为:D.
6.【答案】 B
【解析】因为 , , , ,
所以 ,且函数的图象连续不断,
所以函数 有一个零点所在的区间为 ,故 可能等于1.
故答案为:B
7.【答案】 B
【解析】依题意,画出两个函数的图像如下图所示,
由图可知,两个函数图像有 个交点,
故答案为:B.
8.【答案】 A
【解析】当 时, ,由 , 得 ,当 时, ,由 得 ,所以当 时函数 有三个零点或四个零点,对 ,由 得 ,当 时, 有一个零点;由于 ,所以 有一个零点或两个零点,
故答案为:A.
9.【答案】 B
【解析】解:令 ,则 ,
则 ,
故 ,如图示:
由 ,
得 ,
函数 恒过 , ,
由 , ,
可得 , , ,
若方程 有唯一解,
则 或 ,即 或 ;
当 即图象相切时,
根据 , ,
解得 舍去),
则 的范围是 ,
故答案为:B.
10.【答案】 C
【解析】已知曲线 与曲线 有三个交点,等价于方程 有三个不等的实根,即方程 有三个不等的实根,
令 ,则 ,显然当 时, ,函数 单调递增,且此时 的值域为 ;当 时, ,函数 单调递减,且此时 的值域为 ,
故函数 的最大值为 ,
又因为方程 有三个不等的实根,等价于方程 有两个不等的实根,且一个大于0小于 ,一个小于0,
故可得 ,解得 。
故答案为:C
二、填空题
11.【答案】 23080;52920
【解析】根据全年应纳税所得额×对应档的税率-对应档的速算扣除数,
可得小李的全年应纳税所得额为200000元时,应缴个税为
(元),
当全年应纳税所得额为500000元时,即全年应缴个税为
,
解得 (元).
故答案为:23080;52920
12.【答案】
【解析】解:设 ,因为 ,所以函数函数 存在零点时,则满足m的取值范围是-1 m<0,故答案为
13.【答案】 7
【解析】当 时,
当 时,
当 时,
函数 的实数根的个数; 即方程 的实数根的个数.
在同一坐标系中作出 与 的图象,
由 ,如图,函数 的图象与 的图象有7个交点.
所以函数 的零点个数是:7
故答案为:7
14.【答案】
【解析】 的图象如图: , 是二次函数的一部分, 时取得最大值4, , 是指数函数的一部分的图象, 时, ,由题意可知 .
故答案为: .
15.【答案】
【解析】 在 上单调递增, , , ,因为 ,则 ,所以 ,则 ,所以下一个含根区间应该为 .
故答案为:
16.【答案】 -1
【解析】解:根据题意,则。
故答案为:-1
17.【答案】
【解析】
,
由 ,可得 ,解得 , ,
因为 在区间 内没有零点,
所以 ,且 ,
即 且 ,
因为 ,
分别取 ,1,2,3 ,
,
,
∴ 的取值范围是 ,
故答案为: 。
18.【答案】
【解析】
∵f(x+2)=f(x)﹣f(1),
且f(x)是定义域为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
又f(﹣1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2 ,
函数的图象为开口向下、顶点为(3,0)的抛物线.
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至多有3个交点.
可以分两种情况:其一是有交点时,其二是一个交点也没有,
当一个交点都没有时,即a>1.
当有交点时,∵f(x)≤0,∴g(x)≤0,可得0<a<1,
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至多有三个零点,
则有g(4)
故答案为: 。
三、解答题
19.【答案】 (1)解: 且 ,
当 时, 解得 ;
当 时, 解得 ;
综上可得 或
(2)解:
①当 时,由 在其定义域上单调递增,
解得 ,即
②当 时,由 在其定义域上单调递减,
解得 ,即
20.【答案】 (1)解:当 时, , ,
因此,第10天销售该商品的销售收入是 ;
(2)解:设 .
①当 且 时, ,
,
此时,函数 单调递减, ;
②当 且 时, ,
,
此时,函数 单调递减, .
,因此,这 天中,第一天的销售收入最大,且销售收入的最大值为 元.
21.【答案】 (1)解:根据题意,点C受A干扰指数为 ,点C受B干扰指数为 ,
所以点C处干扰指数为: .
(2)解:因为 ,
所以 ,
当且仅当 ,即 时,取等号,
所以“干扰指数”最小时 所处位置在距A点6公里处.
22.【答案】 (1)解:C1对应的函数为 ,C2对应的函数为 .
(2)解:
所以从小到大依次为
(3)解:计算得
理由如下:
令 ,
由于 ,
则函数 的两个零点
因此整数
