人教新课标A版必修2第二章 点、直线、平面之间的位置关系 单元练习(含答案)
文档属性
| 名称 | 人教新课标A版必修2第二章 点、直线、平面之间的位置关系 单元练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 314.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 14:57:16 | ||
图片预览



文档简介
人教新课标A版必修2第二章
点、直线、平面之间的位置关系
一、单选题
1.(2019高二上·宁波期中)下列命题不正确的是( )
A. 若 ,且 ,则
B. 若 ,且 ,则
C. 若直线 直线 ,则直线 与直线 确定一个平面
D. 三点 确定一个平面.
2.(2020高一下·扬州期末)已知平面 、平面 、平面 、直线 以及直线 ,则下列命题说法错误的是( )
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
3.(2020高二下·盐城期末)若平行六面体 的底面 是边长为2的菱形,且 , ⊥底面ABCD, ,则异面直线 与 所成角的余弦值为( )
A. B. C. D.
4.(2021高一下·三明期末)如图,在三棱锥P—ABC中,点D,E分别为棱PB,BC的中点.若点F在线段AC上,且满足AD 平面PEF,则 的值为( )
A.1 B.2 C. D.
5.(2019·恩施模拟)已知 是两条不同的直线, , 是两个不同的平面,给出下列命题:
①若 , ,则 ;②若 , ,则 ;③若 是异面直线, , , , ,则 ;④若 不平行,则 与 不可能垂直于同一平面.其中为真命题的是( )
A. ②③④ B. ①②③ C. ①③④ D. ①②④
6.(2019高三上·宝坻期中)有下面四个命题,其中正确命题的序号是( )
①“直线 、 不相交”是“直线 、 为异面直线”的充分而不必要条件;②“直线 平面 内所有直线”的充要条件是“ 平面 ”;③“直线 直线 ”的充要条件是“ 平行于 所在的平面”;④“直线 平面 ”的必要而不充分条件是“直线 平行于 内的一条直线.”
A. ①③ B. ②③ C. ②④ D. ③④
7.(2020高三上·潍坊期中)已知 , 为不同直线, , 为不同平面,则下列结论正确的是( )
A. 若 , ,则
B. 若 , , , ,则
C. 若 , , ,则
D. 若 , , ,则
8.(2021·重庆模拟)已知棱长为2的正方体 , 为 的中点,点 在正方体的表面上运动,且 ,则动点 的轨迹长度为( )
A. B. C. D.
9.(2019高二上·佛山月考)如图,矩形 中, , 为边 的中点,将 沿直线 翻折成 .若 为线段 的中点,则在 翻折过程中,下面四个命题中不正确的是( )
A. 是定值 B. 点 在某个球面上运动
C. 存在某个位置,使 D. 存在某个位置,使 平面
二、填空题
10.(2019高一上·蒙山月考)在正方体 中, 与 所成的角等于________.
11.(2019高一上·汪清月考)如图所示,在圆锥 中, 为底面圆的两条直径, ,且 , , 为 的中点,则异面直线 与 所成角的正切值为________.
12.(2019高一上·衡阳月考)在矩形 中, ,现将 沿矩形的对角线 进行翻折,在翻折的过程中,给出下列结论:
①存在某个位置,使得直线 与直线 垂直;
②存在某个位置,使得直线 与直线 垂直;
③存在某个位置,使得直线 与直线 垂直.
其中正确结论的序号是 .
13.(2019高一下·安庆期末)如图,△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,则此图形中有________个直角三角形.
14.(2019高三上·大庆期中)如图,AB为圆O的直径,点C在圆周上 异于点A, ,直线PA垂直于圆O所在的平面,点M是线段PB的中点 有以下四个命题:
① ∥平面 ;
② ∥平面 ;
③ 平面 ;
④平面 平面 .
其中正确的命题的序号是________.
15.(2020高二上·山西月考)已知三棱柱 的侧棱与底面边长都相等, 在底面 内的射影为 的中心,则 与底面 所成角的正弦值等于 .
16.(2019高二上·濠江期中)已知棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别是线段AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x(0①l∥平面ABCD;
②l⊥AC;
③直线l与平面BCC1B1不垂直;
④当x变化时,l不是定直线.
其中不成立的结论是________.(写出所有不成立结论的序号)
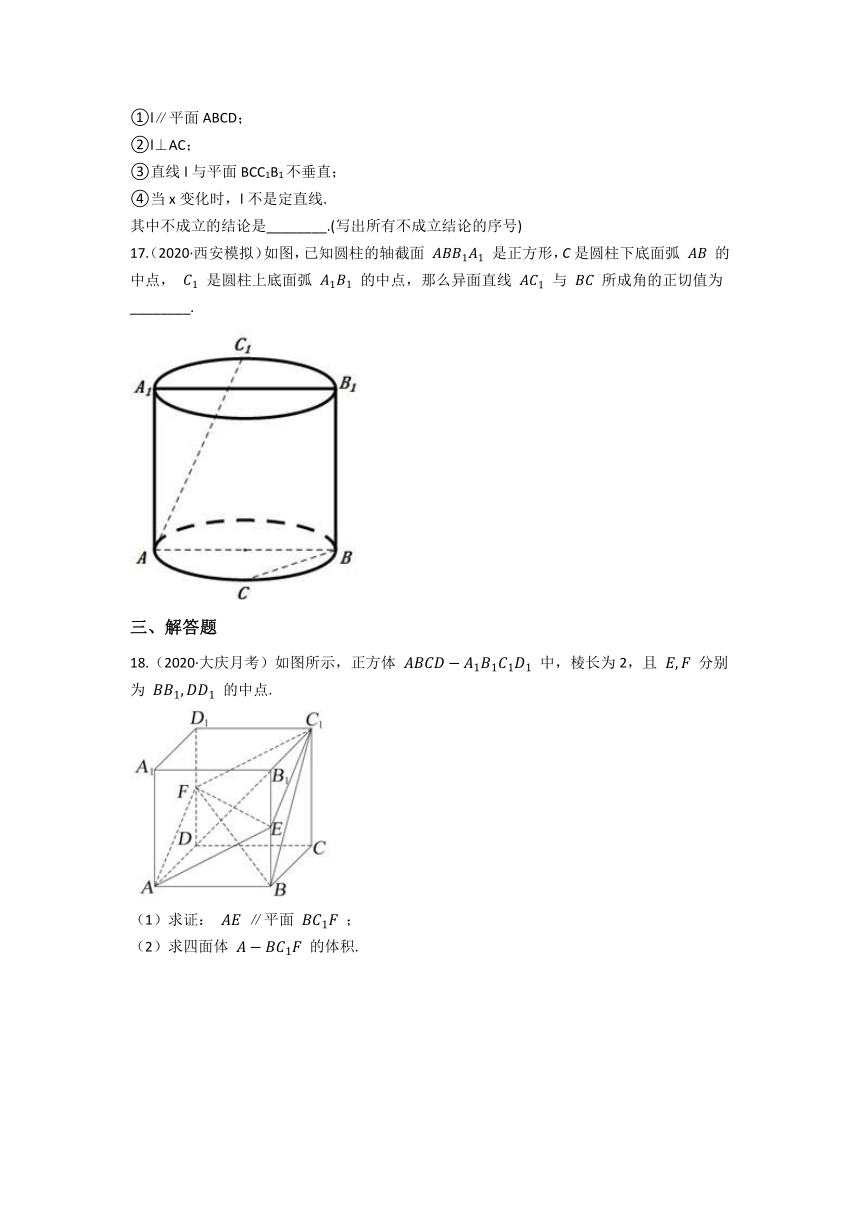
17.(2020·西安模拟)如图,已知圆柱的轴截面 是正方形,C是圆柱下底面弧 的中点, 是圆柱上底面弧 的中点,那么异面直线 与 所成角的正切值为________.
三、解答题
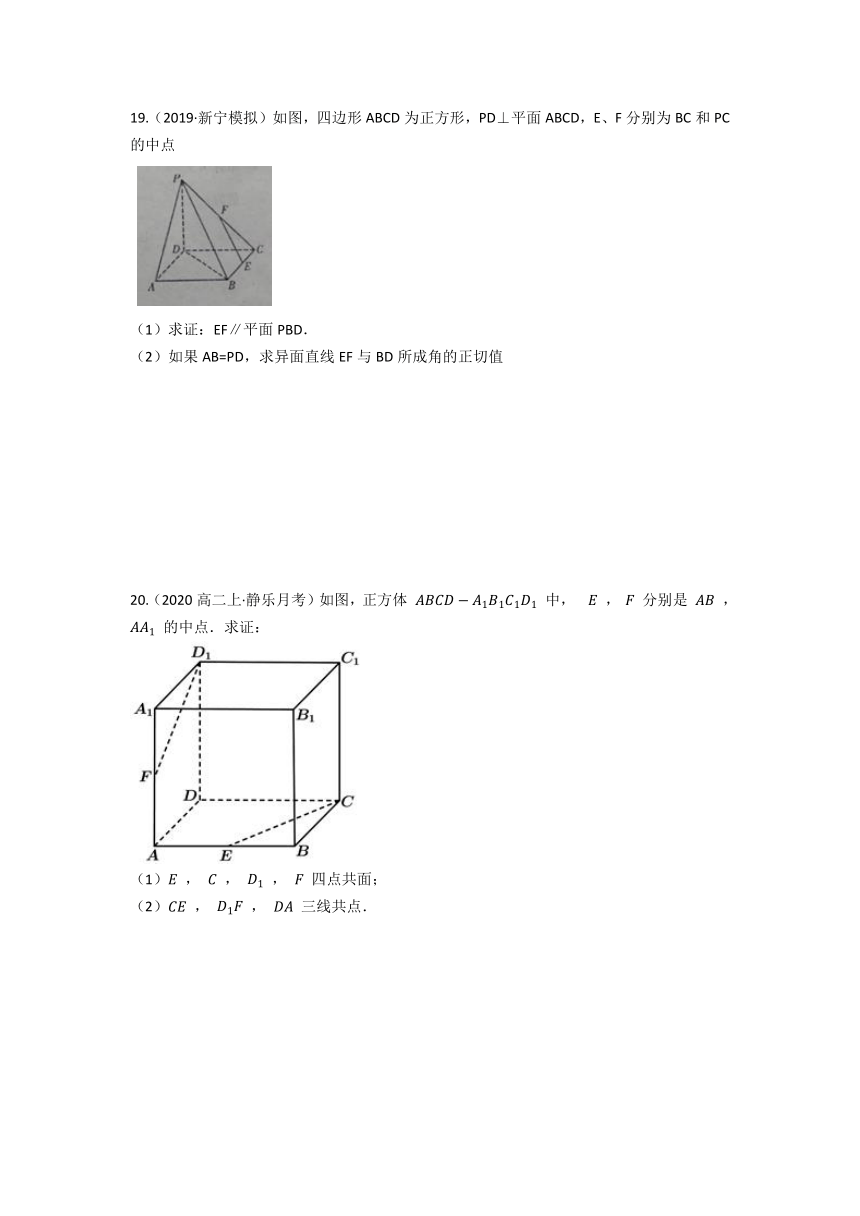
18.(2020·大庆月考)如图所示,正方体 中,棱长为2,且 分别为 的中点.
(1)求证: ∥平面 ;
(2)求四面体 的体积.
19.(2019·新宁模拟)如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点
(1)求证:EF∥平面PBD.
(2)如果AB=PD,求异面直线EF与BD所成角的正切值
20.(2020高二上·静乐月考)如图,正方体 中, , 分别是 , 的中点.求证:
(1) , , , 四点共面;
(2) , , 三线共点.
21.(2020·广东模拟)设三棱锥 的每个顶点都在球 的球面上, 是面积为 的等边三角形, , ,且平面 平面 .
(1)求球 的表面积;
(2)证明:平面 平面 ,且平面 平面 .
(3)与侧面 平行的平面 与棱 , , 分别交于 , , ,求四面体 的体积的最大值.
答案解析部分
一、单选题
1.【答案】 D
【解析】解:对于A:由公理3:如果两个平面有一个公共点,那么它们有且只有一条过该点的直线.A中,平面 与平面 有一个交点 ,则有一条交线,且 在交线上.所以A符合题意.
对于B:由公理1:如果一条直线上的两点在一个平面内,那么这条直线也在此平面内.所以B真确.
对于C:由两条相交直线确定一个平面可知,C符合题意.
对于D:由公理2:不共线的三点确定一个平面可知, 三点共线时不能确定一个平面,所以D不符合题意.
故答案为:D
2.【答案】 D
【解析】A项:因为 , ,所以 , ,A符合题意;
B项:因为两平面平行,分别与第三个平面相交,交线平行,
所以根据 、 、 可证得 ,B符合题意;
C项:因为 ,所以 垂直于平面 内的两条相交直线,
因为 ,所以平面 内的两条相交直线必与平面 内的两条相交直线对应平行,
所以 垂直于平面 内的两条相交直线, ,C符合题意;
D项:
如图所示,绘出正方体 ,
令平面 是平面 ,平面 是平面 ,平面 是平面 ,
则满足 , ,但是 不成立,D不符合题意,
故答案为:D.
3.【答案】 A
【解析】连 交于 , 交于 ,连 ,则 ,
⊥底面ABCD, 底面ABCD,
底面 是边长为2的菱形, ,
,
以点 为坐标原点, 所在的直线分别为 轴建立空间直角坐标系,
,
,
所以异面直线 与 所成角的余弦值为 .
故答案为:A.
4.【答案】 C
【解析】解:连接 ,交 于 ,连接 ,如图,
平面 ,平面 平面 ,
,
点 , 分别为棱 , 的中点.
是 的重心,
.
故答案为:C.
5.【答案】 A
【解析】①若 , ,则 与 位置关系不确定;
②若 ,则 存在直线 与 平行,因为 ,所以 ,则 ;
③当 , , , 时,平面 , 平行;
④逆否命题为:若 与 垂直于同一平面,则 平行,为真命题.
综上,为真命题的是②③④.
故答案为:A
6.【答案】 C
【解析】解:①“直线 、 为异面直线” “直线 、 不相交”,
“直线 、 不相交” 直线 、 的位置关系有平行或异面,故由“直线 、 不相交”得不到“直线 、 为异面直线”
因此“直线 、 不相交”是“直线 、 为异面直线”的必要而不充分条件,因此不正确;
②“直线 平面 内所有直线”的充要条件是“ 平面 ”,正确;
③由“直线 直线 ”则直线 与直线 所在的平面的位置关系有平行、在平面内;
由“ 平行于 所在的平面”则直线 与直线 可能平行,异面;
故“直线 直线 ”与“ 平行于 所在的平面”相互不能推出,
因此不正确;
④由“直线 平面 ” 可得直线 平行平面 内的无数条直线;
由“直线 平行于 内的一条直线”则直线 可能与平面 平行也可能在平面 内;
故“直线 平面 ” “直线 平行于 内的一条直线”,反之不成立,
“直线 平面 ”的必要而不充分条件是“直线 平行于 内的一条直线.”
综上只有②④正确.
故答案为: .
7.【答案】 C
【解析】A选项,若 , ,则 或 ,A不符合题意;
B选项,若 , , , ,当 时, 与 可能相交,B不符合题意;
C选项,若 , ,根据线面垂直的性质,可得 ,又 ,根据面面垂直的判定定理,可得 ,C符合题意;
D选项,若 , , ,垂直于交线,并不能推出垂直于另一平面,因此不能得出 ,即不能推出 .D不符合题意;
故答案为:C.
8.【答案】 C
【解析】由题意知, 在平面 和平面 上的投影分别为 和 ,取 中点 ,连 , ,∵ , ,∴ , ,
故 平面 ,
所以 点的轨迹即为平面 与正方体表面的交线,
取 中点 ,连接 , ,则 ,
∴ , , , 四点共面,
∴ 点的轨迹即为等腰梯形 ,
由正方体棱长为2得 , ,
故轨迹长度为
故答案为:C
9.【答案】 C
【解析】如下图所示,取 的中点 ,连接 、 ,
、 分别为 、 的中点, ,且 ,易证四边形 为平行四边形,则 ,由等角定理得 ,由余弦定理可知 为定值,A、B选项正确;
, 平面 , 平面 , 平面 ,同理可证 平面 , ,则平面 平面 , 平面 , 平面 ,D选项正确;
易知 和 均为等腰直角三角形,且 , ,
,若 ,且 ,可得出 平面 ,
平面 ,则 ,这与 矛盾,C选项错误.
故答案为:C.
二、填空题
10.【答案】
【解析】连结 , ,
则在正方体中,易得 ,
因此 等于 与 所成的角,
因为 , , 均为正方体面对角线,
所以 ,即三角形 为等边三角形,
所以 ,
即 与 所成的角等于 .
故答案为:
11.【答案】
【解析】连接 ,则 ,
即为异面直线 与 所成的角,
又 , , ,
平面 ,
,
即 ,
为直角三角形,
.
12.【答案】 ②
【解析】如下图,
若 ,已知 ,那么 平面 ,则 ,这与 矛盾,点 不会重合,所以①不正确;若 ,已知中 ,则 平面 ,点 在平面 内的射影落在线段 上,并且 ,所以存在某个位置使 ;所以②成立;若 ,已知 ,所以 平面 ,即 ,那 ,这与已知矛盾,所以③不正确。
13.【答案】 4
【解析】∵ 是直角三角形, , 平面 ,
∴ , ,
∵ ,∴ 平面 ,
∴图中直角三角形有 ( 是直角 ), ( 是直角), ( 是直角), ( 是直角),
∴图中直角三角形有4个,
故答案为4.
14.【答案】 ①④
【解析】对①,因为 为 的中点,故 为三角形 的中位线,故 ∥平面 .
故①正确.
对②,因为 平面 ,故②错误.
对③,因为 ,故 不会垂直于 ,故 不垂直于平面 .故③错误
对④, 因为 , 面 ,故 .又 .
故 平面 ,又 平面 ,故平面 平面 .故④正确.
故答案为①④
15.【答案】
【解析】由题意得,不妨设棱长为 ,如图, 在底面 内的射影为 的中心,故 ,由勾股定理得 ,过 作 平面 ,则 为 与底面 所成角,且 ,作 于中点 ,所以 ,所以 ,所以 与底面 所成角的正弦值为 .
16.【答案】 ④
【解析】连接BD,B1D1 , ∵A1P=A1Q=x,∴PQ∥B1D1∥BD∥EF,则PQ∥平面MEF,
又平面MEF∩平面MPQ=l,∴PQ∥l,l∥EF,
∴l∥平面ABCD,故①成立;
又EF⊥AC,∴l⊥AC,故②成立;
∵l∥EF∥BD,故直线l与平面BCC1B1不垂直,故③成立;
当x变化时,l是过点M且与直线EF平行的定直线,故④不成立,
即不成立的结论是④。
17.【答案】
【解析】取圆柱下底面弧 的另一中点 ,连接 ,
则因为C是圆柱下底面弧 的中点,
所以 ,
所以直线 与 所成角等于异面直线 与 所成角.
因为 是圆柱上底面弧 的中点,
所以 圆柱下底面,所以 .
因为圆柱的轴截面 是正方形,
所以 ,
所以直线 与 所成角的正切值为 .
所以异面直线 与 所成角的正切值为 .
故答案为: .
三、解答题
18.【答案】 (1)证明:取 中点为 ,连接 、 ,
因为 是正方体,点 和 为所在棱中点,
所以 ∥ , ,
所以四边形 为平行四边形,
所以 ∥ ,
在正方形 中,点 和 为中点,
所以 ∥ ,
所以 ∥ ,
又因为 平面 , 平面 ,
所以 //平面 .
(2)解:因为 ∥平面 ,
所以 ,
在四面体 中,
,
到平面 的距离为2,
所以 .
19.【答案】 (1)证明: 证明:在△PBC中,E,F为BC和PC的中点,∴EF∥BP,∵EF 平面PBD,
PB 平面PBD,∴EF∥平面PBD.
(2)解:∵在△PBC中,E,F为BC和PC的中点,∴EF∥BP,∴异面直线EF与BD所成角为.
设四边形ABCD的边长为1,则PD=AB=1, ,
在直角三角形PBD中.
20.【答案】 (1)连接 , , ,
, 分别是 , 的中点,
, ,
,
由两条平行线确定一个平面,得到 , , , 四点共面.
(2)分别延长 , ,交于点 ,
, 面 ,
面 .
是 的中点, ,
是 的中点,
连接 , ,
,
, , 三线共点于 .
21.【答案】 (1)解:取 的中点 ,连接 .
因为 ,所以 的外心为 .
因为 ,所以 .
又平面 平面 ,平面 平面 ,所以 平面 ,
所以 在 上.
因为 是等边三角形,所以 是线段 上靠近点 的一个三等分点.
由题意得 ,解得 ,
所以球 的半径 ,球 的表面积为 .
(2)证明:因为 在 上,所以 平面 ,
又 平面 ,所以平面 平面 .
连接 ,则 ,又平面 平面 ,所以 平面 ,
又 平面 ,所以平面 平面 .
(3)解:因为 ,所以 到平面 的距离 .
设 , 到平面 的距离为 .
因为平面 平面 ,所以 ,则 的面积为 .
又 ,所以 到平面 的距离为 ,
所以四面体 的体积 .
设 , ,
当 时, ;当 时, .
所以 ,
即四面体 的体积的最大值为 .
点、直线、平面之间的位置关系
一、单选题
1.(2019高二上·宁波期中)下列命题不正确的是( )
A. 若 ,且 ,则
B. 若 ,且 ,则
C. 若直线 直线 ,则直线 与直线 确定一个平面
D. 三点 确定一个平面.
2.(2020高一下·扬州期末)已知平面 、平面 、平面 、直线 以及直线 ,则下列命题说法错误的是( )
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
3.(2020高二下·盐城期末)若平行六面体 的底面 是边长为2的菱形,且 , ⊥底面ABCD, ,则异面直线 与 所成角的余弦值为( )
A. B. C. D.
4.(2021高一下·三明期末)如图,在三棱锥P—ABC中,点D,E分别为棱PB,BC的中点.若点F在线段AC上,且满足AD 平面PEF,则 的值为( )
A.1 B.2 C. D.
5.(2019·恩施模拟)已知 是两条不同的直线, , 是两个不同的平面,给出下列命题:
①若 , ,则 ;②若 , ,则 ;③若 是异面直线, , , , ,则 ;④若 不平行,则 与 不可能垂直于同一平面.其中为真命题的是( )
A. ②③④ B. ①②③ C. ①③④ D. ①②④
6.(2019高三上·宝坻期中)有下面四个命题,其中正确命题的序号是( )
①“直线 、 不相交”是“直线 、 为异面直线”的充分而不必要条件;②“直线 平面 内所有直线”的充要条件是“ 平面 ”;③“直线 直线 ”的充要条件是“ 平行于 所在的平面”;④“直线 平面 ”的必要而不充分条件是“直线 平行于 内的一条直线.”
A. ①③ B. ②③ C. ②④ D. ③④
7.(2020高三上·潍坊期中)已知 , 为不同直线, , 为不同平面,则下列结论正确的是( )
A. 若 , ,则
B. 若 , , , ,则
C. 若 , , ,则
D. 若 , , ,则
8.(2021·重庆模拟)已知棱长为2的正方体 , 为 的中点,点 在正方体的表面上运动,且 ,则动点 的轨迹长度为( )
A. B. C. D.
9.(2019高二上·佛山月考)如图,矩形 中, , 为边 的中点,将 沿直线 翻折成 .若 为线段 的中点,则在 翻折过程中,下面四个命题中不正确的是( )
A. 是定值 B. 点 在某个球面上运动
C. 存在某个位置,使 D. 存在某个位置,使 平面
二、填空题
10.(2019高一上·蒙山月考)在正方体 中, 与 所成的角等于________.
11.(2019高一上·汪清月考)如图所示,在圆锥 中, 为底面圆的两条直径, ,且 , , 为 的中点,则异面直线 与 所成角的正切值为________.
12.(2019高一上·衡阳月考)在矩形 中, ,现将 沿矩形的对角线 进行翻折,在翻折的过程中,给出下列结论:
①存在某个位置,使得直线 与直线 垂直;
②存在某个位置,使得直线 与直线 垂直;
③存在某个位置,使得直线 与直线 垂直.
其中正确结论的序号是 .
13.(2019高一下·安庆期末)如图,△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,则此图形中有________个直角三角形.
14.(2019高三上·大庆期中)如图,AB为圆O的直径,点C在圆周上 异于点A, ,直线PA垂直于圆O所在的平面,点M是线段PB的中点 有以下四个命题:
① ∥平面 ;
② ∥平面 ;
③ 平面 ;
④平面 平面 .
其中正确的命题的序号是________.
15.(2020高二上·山西月考)已知三棱柱 的侧棱与底面边长都相等, 在底面 内的射影为 的中心,则 与底面 所成角的正弦值等于 .
16.(2019高二上·濠江期中)已知棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别是线段AB、AD、AA1的中点,又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x(0
②l⊥AC;
③直线l与平面BCC1B1不垂直;
④当x变化时,l不是定直线.
其中不成立的结论是________.(写出所有不成立结论的序号)
17.(2020·西安模拟)如图,已知圆柱的轴截面 是正方形,C是圆柱下底面弧 的中点, 是圆柱上底面弧 的中点,那么异面直线 与 所成角的正切值为________.
三、解答题
18.(2020·大庆月考)如图所示,正方体 中,棱长为2,且 分别为 的中点.
(1)求证: ∥平面 ;
(2)求四面体 的体积.
19.(2019·新宁模拟)如图,四边形ABCD为正方形,PD⊥平面ABCD,E、F分别为BC和PC的中点
(1)求证:EF∥平面PBD.
(2)如果AB=PD,求异面直线EF与BD所成角的正切值
20.(2020高二上·静乐月考)如图,正方体 中, , 分别是 , 的中点.求证:
(1) , , , 四点共面;
(2) , , 三线共点.
21.(2020·广东模拟)设三棱锥 的每个顶点都在球 的球面上, 是面积为 的等边三角形, , ,且平面 平面 .
(1)求球 的表面积;
(2)证明:平面 平面 ,且平面 平面 .
(3)与侧面 平行的平面 与棱 , , 分别交于 , , ,求四面体 的体积的最大值.
答案解析部分
一、单选题
1.【答案】 D
【解析】解:对于A:由公理3:如果两个平面有一个公共点,那么它们有且只有一条过该点的直线.A中,平面 与平面 有一个交点 ,则有一条交线,且 在交线上.所以A符合题意.
对于B:由公理1:如果一条直线上的两点在一个平面内,那么这条直线也在此平面内.所以B真确.
对于C:由两条相交直线确定一个平面可知,C符合题意.
对于D:由公理2:不共线的三点确定一个平面可知, 三点共线时不能确定一个平面,所以D不符合题意.
故答案为:D
2.【答案】 D
【解析】A项:因为 , ,所以 , ,A符合题意;
B项:因为两平面平行,分别与第三个平面相交,交线平行,
所以根据 、 、 可证得 ,B符合题意;
C项:因为 ,所以 垂直于平面 内的两条相交直线,
因为 ,所以平面 内的两条相交直线必与平面 内的两条相交直线对应平行,
所以 垂直于平面 内的两条相交直线, ,C符合题意;
D项:
如图所示,绘出正方体 ,
令平面 是平面 ,平面 是平面 ,平面 是平面 ,
则满足 , ,但是 不成立,D不符合题意,
故答案为:D.
3.【答案】 A
【解析】连 交于 , 交于 ,连 ,则 ,
⊥底面ABCD, 底面ABCD,
底面 是边长为2的菱形, ,
,
以点 为坐标原点, 所在的直线分别为 轴建立空间直角坐标系,
,
,
所以异面直线 与 所成角的余弦值为 .
故答案为:A.
4.【答案】 C
【解析】解:连接 ,交 于 ,连接 ,如图,
平面 ,平面 平面 ,
,
点 , 分别为棱 , 的中点.
是 的重心,
.
故答案为:C.
5.【答案】 A
【解析】①若 , ,则 与 位置关系不确定;
②若 ,则 存在直线 与 平行,因为 ,所以 ,则 ;
③当 , , , 时,平面 , 平行;
④逆否命题为:若 与 垂直于同一平面,则 平行,为真命题.
综上,为真命题的是②③④.
故答案为:A
6.【答案】 C
【解析】解:①“直线 、 为异面直线” “直线 、 不相交”,
“直线 、 不相交” 直线 、 的位置关系有平行或异面,故由“直线 、 不相交”得不到“直线 、 为异面直线”
因此“直线 、 不相交”是“直线 、 为异面直线”的必要而不充分条件,因此不正确;
②“直线 平面 内所有直线”的充要条件是“ 平面 ”,正确;
③由“直线 直线 ”则直线 与直线 所在的平面的位置关系有平行、在平面内;
由“ 平行于 所在的平面”则直线 与直线 可能平行,异面;
故“直线 直线 ”与“ 平行于 所在的平面”相互不能推出,
因此不正确;
④由“直线 平面 ” 可得直线 平行平面 内的无数条直线;
由“直线 平行于 内的一条直线”则直线 可能与平面 平行也可能在平面 内;
故“直线 平面 ” “直线 平行于 内的一条直线”,反之不成立,
“直线 平面 ”的必要而不充分条件是“直线 平行于 内的一条直线.”
综上只有②④正确.
故答案为: .
7.【答案】 C
【解析】A选项,若 , ,则 或 ,A不符合题意;
B选项,若 , , , ,当 时, 与 可能相交,B不符合题意;
C选项,若 , ,根据线面垂直的性质,可得 ,又 ,根据面面垂直的判定定理,可得 ,C符合题意;
D选项,若 , , ,垂直于交线,并不能推出垂直于另一平面,因此不能得出 ,即不能推出 .D不符合题意;
故答案为:C.
8.【答案】 C
【解析】由题意知, 在平面 和平面 上的投影分别为 和 ,取 中点 ,连 , ,∵ , ,∴ , ,
故 平面 ,
所以 点的轨迹即为平面 与正方体表面的交线,
取 中点 ,连接 , ,则 ,
∴ , , , 四点共面,
∴ 点的轨迹即为等腰梯形 ,
由正方体棱长为2得 , ,
故轨迹长度为
故答案为:C
9.【答案】 C
【解析】如下图所示,取 的中点 ,连接 、 ,
、 分别为 、 的中点, ,且 ,易证四边形 为平行四边形,则 ,由等角定理得 ,由余弦定理可知 为定值,A、B选项正确;
, 平面 , 平面 , 平面 ,同理可证 平面 , ,则平面 平面 , 平面 , 平面 ,D选项正确;
易知 和 均为等腰直角三角形,且 , ,
,若 ,且 ,可得出 平面 ,
平面 ,则 ,这与 矛盾,C选项错误.
故答案为:C.
二、填空题
10.【答案】
【解析】连结 , ,
则在正方体中,易得 ,
因此 等于 与 所成的角,
因为 , , 均为正方体面对角线,
所以 ,即三角形 为等边三角形,
所以 ,
即 与 所成的角等于 .
故答案为:
11.【答案】
【解析】连接 ,则 ,
即为异面直线 与 所成的角,
又 , , ,
平面 ,
,
即 ,
为直角三角形,
.
12.【答案】 ②
【解析】如下图,
若 ,已知 ,那么 平面 ,则 ,这与 矛盾,点 不会重合,所以①不正确;若 ,已知中 ,则 平面 ,点 在平面 内的射影落在线段 上,并且 ,所以存在某个位置使 ;所以②成立;若 ,已知 ,所以 平面 ,即 ,那 ,这与已知矛盾,所以③不正确。
13.【答案】 4
【解析】∵ 是直角三角形, , 平面 ,
∴ , ,
∵ ,∴ 平面 ,
∴图中直角三角形有 ( 是直角 ), ( 是直角), ( 是直角), ( 是直角),
∴图中直角三角形有4个,
故答案为4.
14.【答案】 ①④
【解析】对①,因为 为 的中点,故 为三角形 的中位线,故 ∥平面 .
故①正确.
对②,因为 平面 ,故②错误.
对③,因为 ,故 不会垂直于 ,故 不垂直于平面 .故③错误
对④, 因为 , 面 ,故 .又 .
故 平面 ,又 平面 ,故平面 平面 .故④正确.
故答案为①④
15.【答案】
【解析】由题意得,不妨设棱长为 ,如图, 在底面 内的射影为 的中心,故 ,由勾股定理得 ,过 作 平面 ,则 为 与底面 所成角,且 ,作 于中点 ,所以 ,所以 ,所以 与底面 所成角的正弦值为 .
16.【答案】 ④
【解析】连接BD,B1D1 , ∵A1P=A1Q=x,∴PQ∥B1D1∥BD∥EF,则PQ∥平面MEF,
又平面MEF∩平面MPQ=l,∴PQ∥l,l∥EF,
∴l∥平面ABCD,故①成立;
又EF⊥AC,∴l⊥AC,故②成立;
∵l∥EF∥BD,故直线l与平面BCC1B1不垂直,故③成立;
当x变化时,l是过点M且与直线EF平行的定直线,故④不成立,
即不成立的结论是④。
17.【答案】
【解析】取圆柱下底面弧 的另一中点 ,连接 ,
则因为C是圆柱下底面弧 的中点,
所以 ,
所以直线 与 所成角等于异面直线 与 所成角.
因为 是圆柱上底面弧 的中点,
所以 圆柱下底面,所以 .
因为圆柱的轴截面 是正方形,
所以 ,
所以直线 与 所成角的正切值为 .
所以异面直线 与 所成角的正切值为 .
故答案为: .
三、解答题
18.【答案】 (1)证明:取 中点为 ,连接 、 ,
因为 是正方体,点 和 为所在棱中点,
所以 ∥ , ,
所以四边形 为平行四边形,
所以 ∥ ,
在正方形 中,点 和 为中点,
所以 ∥ ,
所以 ∥ ,
又因为 平面 , 平面 ,
所以 //平面 .
(2)解:因为 ∥平面 ,
所以 ,
在四面体 中,
,
到平面 的距离为2,
所以 .
19.【答案】 (1)证明: 证明:在△PBC中,E,F为BC和PC的中点,∴EF∥BP,∵EF 平面PBD,
PB 平面PBD,∴EF∥平面PBD.
(2)解:∵在△PBC中,E,F为BC和PC的中点,∴EF∥BP,∴异面直线EF与BD所成角为.
设四边形ABCD的边长为1,则PD=AB=1, ,
在直角三角形PBD中.
20.【答案】 (1)连接 , , ,
, 分别是 , 的中点,
, ,
,
由两条平行线确定一个平面,得到 , , , 四点共面.
(2)分别延长 , ,交于点 ,
, 面 ,
面 .
是 的中点, ,
是 的中点,
连接 , ,
,
, , 三线共点于 .
21.【答案】 (1)解:取 的中点 ,连接 .
因为 ,所以 的外心为 .
因为 ,所以 .
又平面 平面 ,平面 平面 ,所以 平面 ,
所以 在 上.
因为 是等边三角形,所以 是线段 上靠近点 的一个三等分点.
由题意得 ,解得 ,
所以球 的半径 ,球 的表面积为 .
(2)证明:因为 在 上,所以 平面 ,
又 平面 ,所以平面 平面 .
连接 ,则 ,又平面 平面 ,所以 平面 ,
又 平面 ,所以平面 平面 .
(3)解:因为 ,所以 到平面 的距离 .
设 , 到平面 的距离为 .
因为平面 平面 ,所以 ,则 的面积为 .
又 ,所以 到平面 的距离为 ,
所以四面体 的体积 .
设 , ,
当 时, ;当 时, .
所以 ,
即四面体 的体积的最大值为 .
