贵州省威旁中学2012-2013学年高一上学期9月月考数学试题
文档属性
| 名称 | 贵州省威旁中学2012-2013学年高一上学期9月月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 158.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-03 19:26:36 | ||
图片预览



文档简介
贵州省威旁中学2012-2013学年高一上学期9月月考数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数的图象恰好通过个整点,则称函数为阶整点函数.有下列函数
① ② ③ ④
其中是一阶整点函数的是 ( )
A.①②③④ B.①③④ C.④ D.①④
【答案】D
2.函数的一个零点在区间内,则实数的取值范围是( )
A. B. C. D.
【答案】C
3. 已知映射,其中,对应法则若对实数,在集合A中不存在原象,则k的取值范围是 ( )
A. B. C. D.
【答案】B
4. 若,,则与的关系是( )
A. B.
C. D.
【答案】A
5.定义一种运算:,已知函数,那么函数的大致图象是( )
【答案】B
6.已知函数f(x)满足:当x≥4时,f(x)=x;当x<4时,f(x)=f(x+1).则f(3)=( )
A. B.8
C. D.16
【答案】C
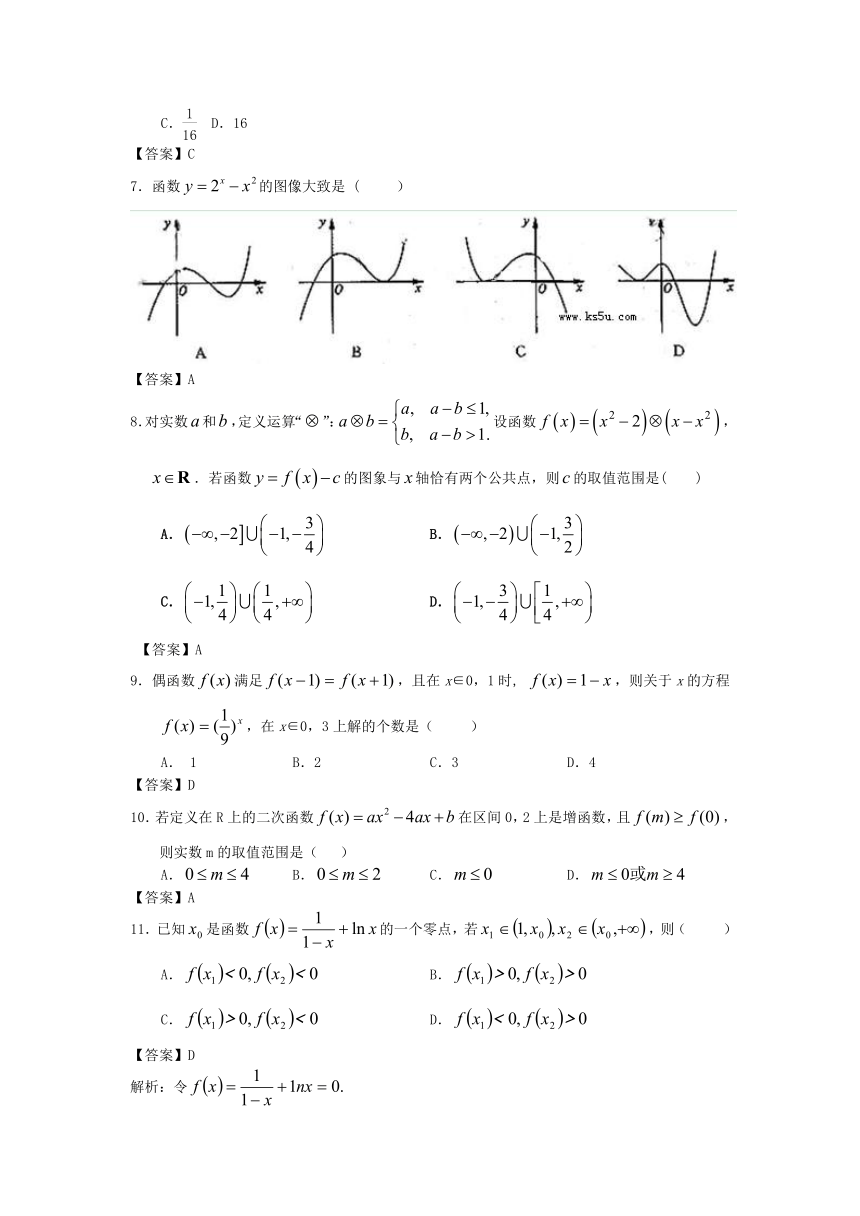
7.函数的图像大致是 ( )
【答案】A
8.对实数和,定义运算“”:设函数, .若函数的图象与轴恰有两个公共点,则的取值范围是( )
A. B.
C. D.
【答案】A
9.偶函数满足,且在x∈0,1时, ,则关于x的方程,在x∈0,3上解的个数是( )
A. 1 B.2 C.3 D.4
【答案】D
10.若定义在R上的二次函数在区间0,2上是增函数,且,则实数m的取值范围是( )
A. B. C. D.
【答案】A
11.已知是函数的一个零点,若,则( )
A. B.
C. D.
【答案】D
解析:令
从而有,此方程的解即为函数的零点.在同一坐标系中作出函数的图象如图所示.
由图象易知,,从而故
12. 三个数的大小顺序是 ( )
A. B.
C. D.
【答案】A
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.若函数y=loga(x+b)(a>0,a≠1)的图象过两点(-1,0)和(0,1),则a=_______,
b=_______.
【答案】2 , 2
14.已知点在直线上,则的最小值为 .
【答案】
15. 若函数,在上单调递减,则的取值范围是 .
【答案】
16.若函数f(x)=若f(a)>f(-a),则实数a的取值范围是________.
【答案】(-1,0)∪(1,+∞)
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.已知函数y=x+有如下性质:如果常数a>0,那么该函数在(0, 上是减函数,在,+∞)上是增函数.
(1)如果函数y=x+在(0,4上是减函数,在4,+∞)上是增函数,求实常数b的值;
(2)设常数c∈1,4,求函数f(x)=x+(1≤x≤2)的最大值和最小值.
【答案】 (1)由函数y=x+的性质知:y=x+在(0,上是减函数,在 ,+∞)上是增函数,
∴=4,∴2b=16=24,∴b=4.
(2)∵c∈1,4,∴∈1,2.
又∵f(x)=x+在(0, 上是减函数,在,+∞)上是增函数,
∴在x∈1,2上,当x= 时,函数取得最小值2 .
又f(1)=1+c,f(2)=2+,
f(2)-f(1)=1-.
当c∈1,2)时,f(2)-f(1)>0,f(2)>f(1),
此时f(x)的最大值为f(2)=2+.
当c=2时,f(2)-f(1)=0,f(2)=f(1),
此时f(x)的最大值为f(2)=f(1)=3.
当c∈(2,4时,f(2)-f(1)<0,f(2)此时f(x)的最大值为f(1)=1+c.
综上所述,函数f(x)的最小值为2;
当c∈1,2)时,函数f(x)的最大值为2+;
当c=2时,函数f(x)的最大值为3;
当c∈(2,4时,函数f(x)的最大值为1+c.
18. 如图是一个二次函数的图象.
(1)写出这个二次函数的零点;
(2)写出这个二次函数的解析式及时函数的值域
【答案】(1)由图可知这个二次函数的零点为
(2)可设两点式,又过点,代入得, ,
其在中,时递增,时递减,最大值为
又,最大值为0,时函数的值域为
19.已知函数f(x)=x2+2ax+2,x∈-5,5.
(1)当a=-1时,求f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间-5,5上是单调函数.
【答案】(1)当a=-1时,
f(x)=x2-2x+2=(x-1)2+1,x∈-5,5.
由于f(x)的对称轴为x=1,结合图象知,
当x=1时,f(x)的最小值为1,
当x=-5时,f(x)的最大值为37.
(2)函数f(x)=(x+a)2+2-a2的图象的对称轴为x=-a,
∵f(x)在区间-5,5上是单调函数,
∴-a≤-5或-a≥5.
故a的取值范围是a≤-5或a≥5.
20.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
【答案】(1)当每辆车月租金为3600元时,未租出的车辆数为 =12,所以这时租出了88辆.
(2)设每辆车的月租金定为x元,则公司月收益为
f(x)=(100-)(x-150)-×50
整理得:f(x)=-+162x-2100=-(x-4050)2+307050
∴当x=4050时,f(x)最大,最大值为f(4050)=307050 元
21.化简或求值:
(1)
(2)。
【答案】(1) 原式==2×22×33+2 — 7— 2+ 1 =210
(2):分子=;
分母=;原式=1。
22.已知函数,
(Ⅰ)当时,求该函数的定义域和值域;
(Ⅱ)如果在区间上恒成立,求实数的取值范围.
【答案】 (1) 当时,
令,解得
所以函数的定义域为.
令,则
所以
因此函数的值域为
(2) 解法一:在区间上恒成立等价于在区间上恒成立
令
当时,,所以满足题意.
当时,是二次函数,对称轴为,
当时,,函数在区间上是增函数,,解得;
当时, ,,解得
当时,,,解得
综上,的取值范围是
解法二:在区间上恒成立等价于在区间上恒成立
由且时,,得
令,则
所以在区间上是增函数,所以
因此的取值范围是.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数的图象恰好通过个整点,则称函数为阶整点函数.有下列函数
① ② ③ ④
其中是一阶整点函数的是 ( )
A.①②③④ B.①③④ C.④ D.①④
【答案】D
2.函数的一个零点在区间内,则实数的取值范围是( )
A. B. C. D.
【答案】C
3. 已知映射,其中,对应法则若对实数,在集合A中不存在原象,则k的取值范围是 ( )
A. B. C. D.
【答案】B
4. 若,,则与的关系是( )
A. B.
C. D.
【答案】A
5.定义一种运算:,已知函数,那么函数的大致图象是( )
【答案】B
6.已知函数f(x)满足:当x≥4时,f(x)=x;当x<4时,f(x)=f(x+1).则f(3)=( )
A. B.8
C. D.16
【答案】C
7.函数的图像大致是 ( )
【答案】A
8.对实数和,定义运算“”:设函数, .若函数的图象与轴恰有两个公共点,则的取值范围是( )
A. B.
C. D.
【答案】A
9.偶函数满足,且在x∈0,1时, ,则关于x的方程,在x∈0,3上解的个数是( )
A. 1 B.2 C.3 D.4
【答案】D
10.若定义在R上的二次函数在区间0,2上是增函数,且,则实数m的取值范围是( )
A. B. C. D.
【答案】A
11.已知是函数的一个零点,若,则( )
A. B.
C. D.
【答案】D
解析:令
从而有,此方程的解即为函数的零点.在同一坐标系中作出函数的图象如图所示.
由图象易知,,从而故
12. 三个数的大小顺序是 ( )
A. B.
C. D.
【答案】A
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.若函数y=loga(x+b)(a>0,a≠1)的图象过两点(-1,0)和(0,1),则a=_______,
b=_______.
【答案】2 , 2
14.已知点在直线上,则的最小值为 .
【答案】
15. 若函数,在上单调递减,则的取值范围是 .
【答案】
16.若函数f(x)=若f(a)>f(-a),则实数a的取值范围是________.
【答案】(-1,0)∪(1,+∞)
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.已知函数y=x+有如下性质:如果常数a>0,那么该函数在(0, 上是减函数,在,+∞)上是增函数.
(1)如果函数y=x+在(0,4上是减函数,在4,+∞)上是增函数,求实常数b的值;
(2)设常数c∈1,4,求函数f(x)=x+(1≤x≤2)的最大值和最小值.
【答案】 (1)由函数y=x+的性质知:y=x+在(0,上是减函数,在 ,+∞)上是增函数,
∴=4,∴2b=16=24,∴b=4.
(2)∵c∈1,4,∴∈1,2.
又∵f(x)=x+在(0, 上是减函数,在,+∞)上是增函数,
∴在x∈1,2上,当x= 时,函数取得最小值2 .
又f(1)=1+c,f(2)=2+,
f(2)-f(1)=1-.
当c∈1,2)时,f(2)-f(1)>0,f(2)>f(1),
此时f(x)的最大值为f(2)=2+.
当c=2时,f(2)-f(1)=0,f(2)=f(1),
此时f(x)的最大值为f(2)=f(1)=3.
当c∈(2,4时,f(2)-f(1)<0,f(2)
综上所述,函数f(x)的最小值为2;
当c∈1,2)时,函数f(x)的最大值为2+;
当c=2时,函数f(x)的最大值为3;
当c∈(2,4时,函数f(x)的最大值为1+c.
18. 如图是一个二次函数的图象.
(1)写出这个二次函数的零点;
(2)写出这个二次函数的解析式及时函数的值域
【答案】(1)由图可知这个二次函数的零点为
(2)可设两点式,又过点,代入得, ,
其在中,时递增,时递减,最大值为
又,最大值为0,时函数的值域为
19.已知函数f(x)=x2+2ax+2,x∈-5,5.
(1)当a=-1时,求f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间-5,5上是单调函数.
【答案】(1)当a=-1时,
f(x)=x2-2x+2=(x-1)2+1,x∈-5,5.
由于f(x)的对称轴为x=1,结合图象知,
当x=1时,f(x)的最小值为1,
当x=-5时,f(x)的最大值为37.
(2)函数f(x)=(x+a)2+2-a2的图象的对称轴为x=-a,
∵f(x)在区间-5,5上是单调函数,
∴-a≤-5或-a≥5.
故a的取值范围是a≤-5或a≥5.
20.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
【答案】(1)当每辆车月租金为3600元时,未租出的车辆数为 =12,所以这时租出了88辆.
(2)设每辆车的月租金定为x元,则公司月收益为
f(x)=(100-)(x-150)-×50
整理得:f(x)=-+162x-2100=-(x-4050)2+307050
∴当x=4050时,f(x)最大,最大值为f(4050)=307050 元
21.化简或求值:
(1)
(2)。
【答案】(1) 原式==2×22×33+2 — 7— 2+ 1 =210
(2):分子=;
分母=;原式=1。
22.已知函数,
(Ⅰ)当时,求该函数的定义域和值域;
(Ⅱ)如果在区间上恒成立,求实数的取值范围.
【答案】 (1) 当时,
令,解得
所以函数的定义域为.
令,则
所以
因此函数的值域为
(2) 解法一:在区间上恒成立等价于在区间上恒成立
令
当时,,所以满足题意.
当时,是二次函数,对称轴为,
当时,,函数在区间上是增函数,,解得;
当时, ,,解得
当时,,,解得
综上,的取值范围是
解法二:在区间上恒成立等价于在区间上恒成立
由且时,,得
令,则
所以在区间上是增函数,所以
因此的取值范围是.
