2021-2022学年鲁教版(五四制)九年级数学下册5.3垂径定理同步练习题(word解析版)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.3垂径定理同步练习题(word解析版) | 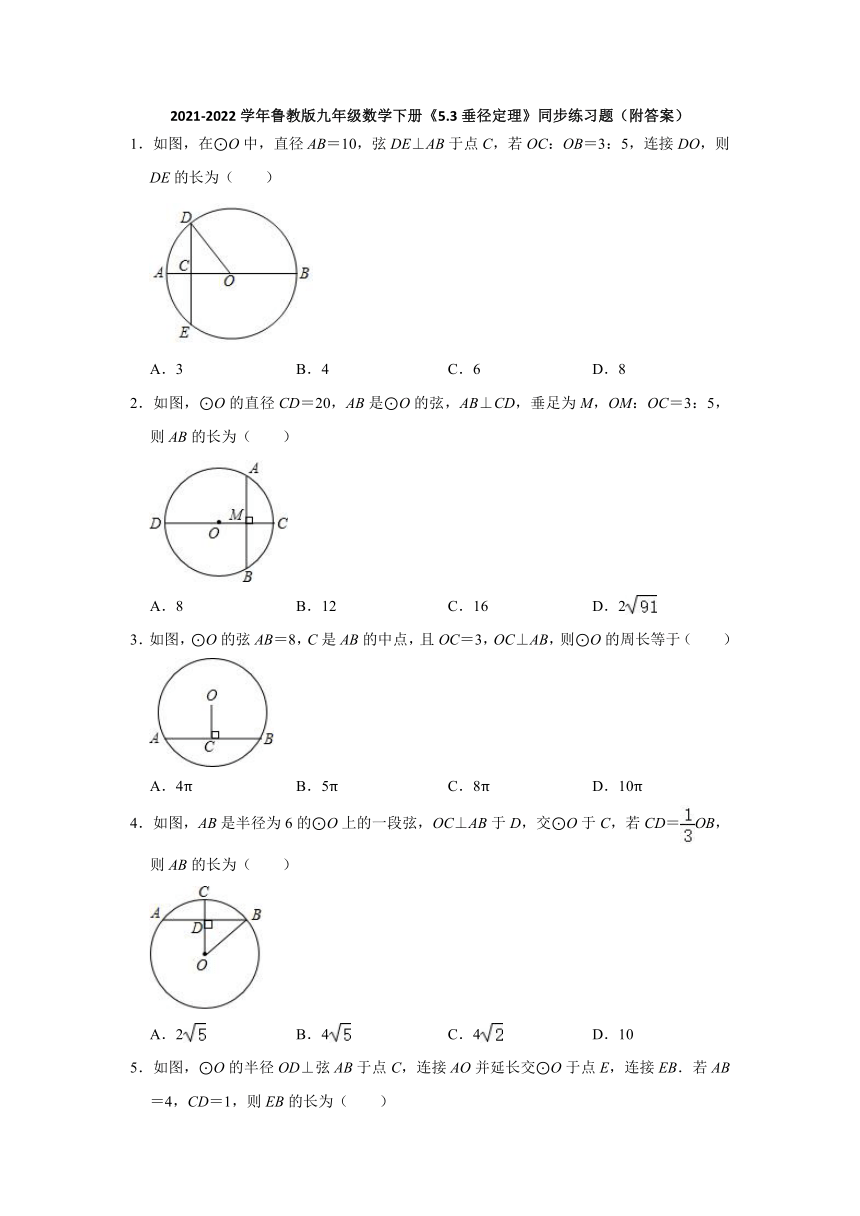 | |
| 格式 | doc | ||
| 文件大小 | 317.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 06:46:47 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学下册《5.3垂径定理》同步练习题(附答案)
1.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
2.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8 B.12 C.16 D.2
3.如图,⊙O的弦AB=8,C是AB的中点,且OC=3,OC⊥AB,则⊙O的周长等于( )
A.4π B.5π C.8π D.10π
4.如图,AB是半径为6的⊙O上的一段弦,OC⊥AB于D,交⊙O于C,若CD=OB,则AB的长为( )
A.2 B.4 C.4 D.10
5.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EB.若AB=4,CD=1,则EB的长为( )
A.3 B.4 C.5 D.2.5
6.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m B.24m C.30m D.60m
7.如图,圆O的弦AB⊥OC,且将半径OC分为2:1的两部分(OD:DC=2:1),AB=4,则圆O的半径为( )
A.3 B.5 C.6 D.9
8.如图,CD为圆O的直径,弦AB⊥CD,垂足为E,CE=1,半径为25,则弦AB的长为( )
A.24 B.14 C.10 D.7
9.如图,⊙O的半径为6,直径CD过弦EF的中点G,若∠EOD=60°,则弦CF的长等于( )
A.6 B.6 C.3 D.9
10.如图,CD是⊙O的直径,弦AB⊥CD,垂足为M,若CM=8,DM=12,则AB等于( )
A.4 B.8 C.8 D.4
11.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
12.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm C.2cm或4cm D.2cm或4cm
13.如图,⊙O的直径CD垂直于弦AB,垂足为P,若⊙O的半径为5cm,AB=8cm,则PD的长为 cm.
14.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,AO=5,则OF的长度是 .
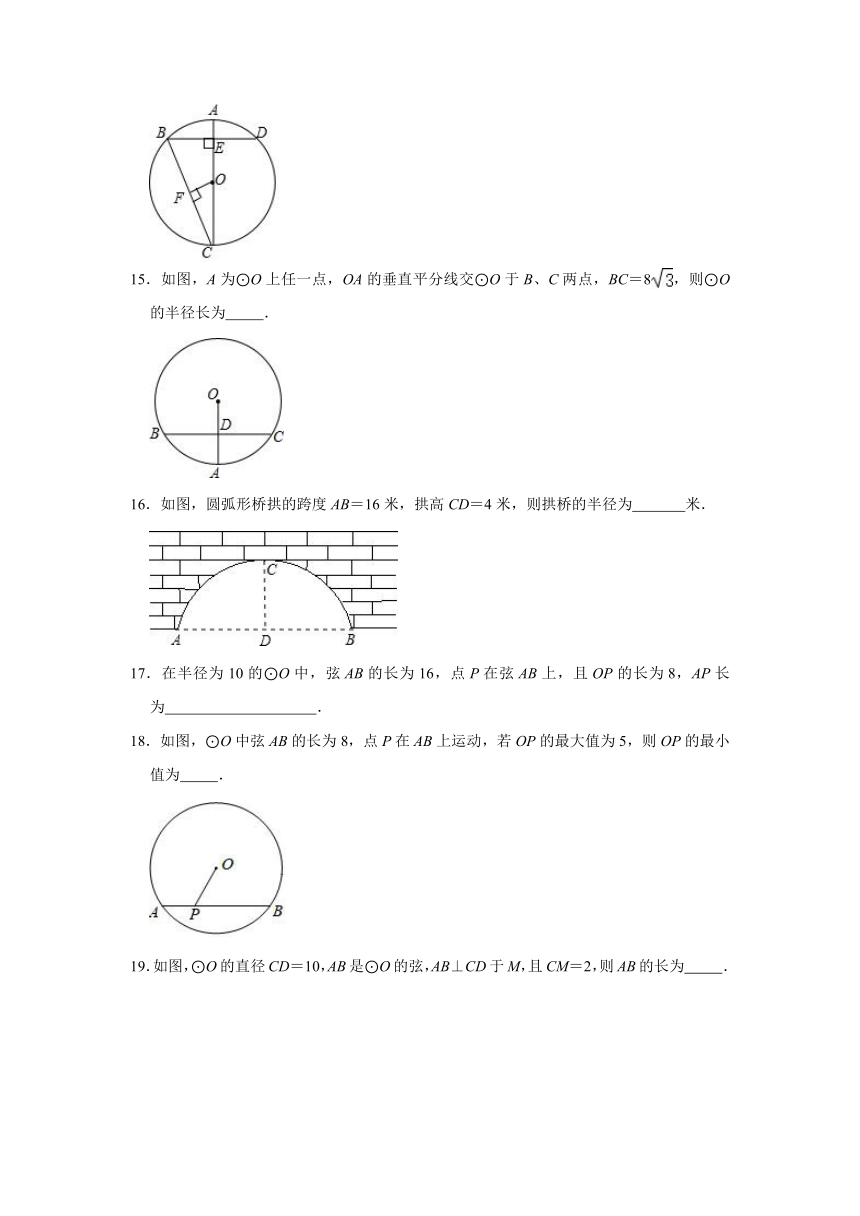
15.如图,A为⊙O上任一点,OA的垂直平分线交⊙O于B、C两点,BC=8,则⊙O的半径长为 .
16.如图,圆弧形桥拱的跨度AB=16米,拱高CD=4米,则拱桥的半径为 米.
17.在半径为10的⊙O中,弦AB的长为16,点P在弦AB上,且OP的长为8,AP长为 .
18.如图,⊙O中弦AB的长为8,点P在AB上运动,若OP的最大值为5,则OP的最小值为 .
19.如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD于M,且CM=2,则AB的长为 .
20.如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交于D.若BC=8,ED=2,求⊙O的半径.
21.如图A、B是⊙O上的两点,∠AOB=120°,C是弧的中点,求证四边形OACB是菱形.
参考答案
1.解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
2.解:连接OA,
∵⊙O的直径CD=20,OM:OC=3:5,
∴OC=10,OM=6,
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选:C.
3.解:连接OA,如图,
∵C是AB的中点,
∴AC=BC=AB=4,OC⊥AB,
在Rt△OAC中,OA===5,
∴⊙O的周长=2π×5=10π.
故选:D.
4.解:∵OC⊥AB,
∴AD=DB,∠ODB=90°
∵CD=OB,OB=6,
∴CD=2,OD=4,
∴BD===2,
∴AB=2BD=4,
故选:B.
5.解:设⊙O的半径为r.
∵OD⊥AB,
∴AC=BC=2,
在Rt△AOC中,∵∠ACO=90°,
∴OA2=OC2+AC2,
∴r2=(r﹣1)2+22,
∴r=,
∴OC=,
∵OA=OE,AC=CB,
∴BE=2OC=3,
故选:A.
6.解:∵OC⊥AB,AB=40 m,
∴AD=DB=20 m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25(m),
∴这段弯路的半径为25 m
故选:A.
7.解:设OD=2a,则CD=a,OA=2a,
∵AB⊥OC,OC为半径,
∴AD=BD=AB=×4=2,
在Rt△ODA中,由勾股定理得:(3a)2=(2a)2+(2)2,
a=2(负数舍去),
OA=3×2=6,
故选:C.
8.解:连接OA,
∵CD为圆O的直径,弦AB⊥CD,
∴AE=EB,
由题意得,OE=OC﹣CE=24,
在Rt△AOE中,AE==7,
∴AB=2AE=14,
故选:B.
9.解:连接DF,
∵直径CD过弦EF的中点G,
∴=,
∴∠DCF=∠EOD=30°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴CF=CD cos∠DCF=12×=6,
故选:B.
10.解:如图,连接OA,
∵CD是⊙O的直径,CM=8,DM=12,
∴OA=OC=10,AM=BM,
∴OM=OC﹣CM=10﹣8=2,
在Rt△AOM中,由勾股定理可得AM===4,
∴AB=2AM=8,
故选:C.
11.解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=∠APC=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH==,
∴CD=2CH=2.
故选:C.
12.解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4(cm),OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2(cm),
在Rt△AMC中,AC===2(cm).
故选:C.
13.解:连接OA,
∵CD⊥AB,
∴∠APO=90°,PA=PB=,
在Rt△OAP中,OP2+PA2=OA2,
∴OP2+42=52,
解得OP=3,
∴PD=OD﹣OP=5﹣3=2(cm)
故答案为2.
14.解:连接OB,
∵弦BD⊥AO,
∴BE=BD=4,
由勾股定理得,OE==3,
则CE=OC+OE=8,
∴BC==4,
∵OF⊥BC,
∴CF=BF=2,
∵∠CFO=∠CEB=90°,∠C=∠C,
∴△CFO∽△CEB,
∴=,即=,
解得,OF=,
故答案为:.
15.解:连接OB,如图,
∵BC垂直平分OA,
∴OD=OA,
而OB=OA,
∴OD=OB,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=CD=BC= 8=4,
在Rt△OBD中,∵∠B=30°,
∴OD=BD=4,
∴OB=2OD=8,
即⊙O的半径长为8.
故答案为8.
16.解:设所在的圆的圆心是O.
根据垂径定理,知C,O,D三点共线,
设圆的半径是r,则根据垂径定理和勾股定理,得r2=(r﹣4)2+64,∴r=10m.
17.解:作OC⊥AB于点C,
∴AC=AB=8,
由勾股定理得,OC==6,
∴PC==2,
当点P在线段AC上时,AP=AC﹣PC=8﹣2,
当点P在线段BC上时,AP=8+2,
故答案为:8﹣2或8+2.
18.解:连接OA,作OH⊥AB于H.
∵当点P与A重合时,OP的值最大,
∴OA=5,
∵OH⊥AB,
∴AH=HB=4,
在Rt△AOH中,∵OA=5,AH=4,
∴OH==3,
根据垂线段最短可知:当点P与H重合时,OP的值最小,最小值为3.
故答案为3.
19.解:连接OA.则OA=OC=CD=5.
则OM=OC﹣CM=5﹣3=3.
在直角△OAM中,AM===4.
∵AB⊥CD于M,
∴AB=2AM=8.
故答案是:8.
20.解:连接OC,
∵AB是⊙O的直径,BC是弦,OD⊥BC于E,
∴OD垂直平分BC,
∵BC=8,ED=2
设半径为R,则CE=4,OE=R﹣2,
∴R2=(R﹣2)2+42
∴R=5.
答:⊙O的半径是5.
21.证明:连OC,如图,
∵C是的中点,∠AOB=l20°
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,
∴四边形OACB是菱形.
1.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
2.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
A.8 B.12 C.16 D.2
3.如图,⊙O的弦AB=8,C是AB的中点,且OC=3,OC⊥AB,则⊙O的周长等于( )
A.4π B.5π C.8π D.10π
4.如图,AB是半径为6的⊙O上的一段弦,OC⊥AB于D,交⊙O于C,若CD=OB,则AB的长为( )
A.2 B.4 C.4 D.10
5.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EB.若AB=4,CD=1,则EB的长为( )
A.3 B.4 C.5 D.2.5
6.如图,一条公路的转弯处是一段圆弧(),点O是这段弧所在圆的圆心,AB=40m,点C是的中点,点D是AB的中点,且CD=10m,则这段弯路所在圆的半径为( )
A.25m B.24m C.30m D.60m
7.如图,圆O的弦AB⊥OC,且将半径OC分为2:1的两部分(OD:DC=2:1),AB=4,则圆O的半径为( )
A.3 B.5 C.6 D.9
8.如图,CD为圆O的直径,弦AB⊥CD,垂足为E,CE=1,半径为25,则弦AB的长为( )
A.24 B.14 C.10 D.7
9.如图,⊙O的半径为6,直径CD过弦EF的中点G,若∠EOD=60°,则弦CF的长等于( )
A.6 B.6 C.3 D.9
10.如图,CD是⊙O的直径,弦AB⊥CD,垂足为M,若CM=8,DM=12,则AB等于( )
A.4 B.8 C.8 D.4
11.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
12.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
A.2cm B.4cm C.2cm或4cm D.2cm或4cm
13.如图,⊙O的直径CD垂直于弦AB,垂足为P,若⊙O的半径为5cm,AB=8cm,则PD的长为 cm.
14.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8,AO=5,则OF的长度是 .
15.如图,A为⊙O上任一点,OA的垂直平分线交⊙O于B、C两点,BC=8,则⊙O的半径长为 .
16.如图,圆弧形桥拱的跨度AB=16米,拱高CD=4米,则拱桥的半径为 米.
17.在半径为10的⊙O中,弦AB的长为16,点P在弦AB上,且OP的长为8,AP长为 .
18.如图,⊙O中弦AB的长为8,点P在AB上运动,若OP的最大值为5,则OP的最小值为 .
19.如图,⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD于M,且CM=2,则AB的长为 .
20.如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交于D.若BC=8,ED=2,求⊙O的半径.
21.如图A、B是⊙O上的两点,∠AOB=120°,C是弧的中点,求证四边形OACB是菱形.
参考答案
1.解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
2.解:连接OA,
∵⊙O的直径CD=20,OM:OC=3:5,
∴OC=10,OM=6,
∵AB⊥CD,
∴AM===8,
∴AB=2AM=16.
故选:C.
3.解:连接OA,如图,
∵C是AB的中点,
∴AC=BC=AB=4,OC⊥AB,
在Rt△OAC中,OA===5,
∴⊙O的周长=2π×5=10π.
故选:D.
4.解:∵OC⊥AB,
∴AD=DB,∠ODB=90°
∵CD=OB,OB=6,
∴CD=2,OD=4,
∴BD===2,
∴AB=2BD=4,
故选:B.
5.解:设⊙O的半径为r.
∵OD⊥AB,
∴AC=BC=2,
在Rt△AOC中,∵∠ACO=90°,
∴OA2=OC2+AC2,
∴r2=(r﹣1)2+22,
∴r=,
∴OC=,
∵OA=OE,AC=CB,
∴BE=2OC=3,
故选:A.
6.解:∵OC⊥AB,AB=40 m,
∴AD=DB=20 m,
在Rt△AOD中,OA2=OD2+AD2,
设半径为r得:r2=(r﹣10)2+202,
解得:r=25(m),
∴这段弯路的半径为25 m
故选:A.
7.解:设OD=2a,则CD=a,OA=2a,
∵AB⊥OC,OC为半径,
∴AD=BD=AB=×4=2,
在Rt△ODA中,由勾股定理得:(3a)2=(2a)2+(2)2,
a=2(负数舍去),
OA=3×2=6,
故选:C.
8.解:连接OA,
∵CD为圆O的直径,弦AB⊥CD,
∴AE=EB,
由题意得,OE=OC﹣CE=24,
在Rt△AOE中,AE==7,
∴AB=2AE=14,
故选:B.
9.解:连接DF,
∵直径CD过弦EF的中点G,
∴=,
∴∠DCF=∠EOD=30°,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴CF=CD cos∠DCF=12×=6,
故选:B.
10.解:如图,连接OA,
∵CD是⊙O的直径,CM=8,DM=12,
∴OA=OC=10,AM=BM,
∴OM=OC﹣CM=10﹣8=2,
在Rt△AOM中,由勾股定理可得AM===4,
∴AB=2AM=8,
故选:C.
11.解:作OH⊥CD于H,连接OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=∠APC=30°,
∴∠POH=60°,
∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH==,
∴CD=2CH=2.
故选:C.
12.解:连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4(cm),OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3(cm),
∴CM=OC+OM=5+3=8(cm),
∴AC===4(cm);
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2(cm),
在Rt△AMC中,AC===2(cm).
故选:C.
13.解:连接OA,
∵CD⊥AB,
∴∠APO=90°,PA=PB=,
在Rt△OAP中,OP2+PA2=OA2,
∴OP2+42=52,
解得OP=3,
∴PD=OD﹣OP=5﹣3=2(cm)
故答案为2.
14.解:连接OB,
∵弦BD⊥AO,
∴BE=BD=4,
由勾股定理得,OE==3,
则CE=OC+OE=8,
∴BC==4,
∵OF⊥BC,
∴CF=BF=2,
∵∠CFO=∠CEB=90°,∠C=∠C,
∴△CFO∽△CEB,
∴=,即=,
解得,OF=,
故答案为:.
15.解:连接OB,如图,
∵BC垂直平分OA,
∴OD=OA,
而OB=OA,
∴OD=OB,
∴∠OBD=30°,
∵OD⊥BC,
∴BD=CD=BC= 8=4,
在Rt△OBD中,∵∠B=30°,
∴OD=BD=4,
∴OB=2OD=8,
即⊙O的半径长为8.
故答案为8.
16.解:设所在的圆的圆心是O.
根据垂径定理,知C,O,D三点共线,
设圆的半径是r,则根据垂径定理和勾股定理,得r2=(r﹣4)2+64,∴r=10m.
17.解:作OC⊥AB于点C,
∴AC=AB=8,
由勾股定理得,OC==6,
∴PC==2,
当点P在线段AC上时,AP=AC﹣PC=8﹣2,
当点P在线段BC上时,AP=8+2,
故答案为:8﹣2或8+2.
18.解:连接OA,作OH⊥AB于H.
∵当点P与A重合时,OP的值最大,
∴OA=5,
∵OH⊥AB,
∴AH=HB=4,
在Rt△AOH中,∵OA=5,AH=4,
∴OH==3,
根据垂线段最短可知:当点P与H重合时,OP的值最小,最小值为3.
故答案为3.
19.解:连接OA.则OA=OC=CD=5.
则OM=OC﹣CM=5﹣3=3.
在直角△OAM中,AM===4.
∵AB⊥CD于M,
∴AB=2AM=8.
故答案是:8.
20.解:连接OC,
∵AB是⊙O的直径,BC是弦,OD⊥BC于E,
∴OD垂直平分BC,
∵BC=8,ED=2
设半径为R,则CE=4,OE=R﹣2,
∴R2=(R﹣2)2+42
∴R=5.
答:⊙O的半径是5.
21.证明:连OC,如图,
∵C是的中点,∠AOB=l20°
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,
∴四边形OACB是菱形.
