2020-2021学年鲁教版九年级数学下册5.6 直线与圆的位置关系同步练习(word解析版)
文档属性
| 名称 | 2020-2021学年鲁教版九年级数学下册5.6 直线与圆的位置关系同步练习(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 314.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-24 06:50:48 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学下册《5.6直线与圆的位置关系》同步练习题(附答案)
1.在Rt△ABC中,∠C=90°,AC=8cm,AB=10cm,以C为圆心,以9cm长为直径的⊙C与直线AB的位置关系为( )
A.相交 B.相离 C.相切 D.相离或相交
2.已知⊙O的半径为5cm,点O到同一平面内直线l的距离为6cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.如图,已知BC与⊙O相切于点B,CO的延长线交⊙O于点A,连接AB,若BC=2,AC=6,则⊙O的半径为( )
A.1.5 B.2 C.2.5 D.3
4.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D.连接BD,∠C=36°,则∠B的度数是( )
A.27° B.30° C.36° D.54°
5.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC C.CD=DB D.AC∥OD
6.下列命题中,假命题是( )
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
7.下列说法中错误的有( )
①圆的切线垂直于半径;②圆的切线垂直于过切点的半径;③过半径端点的垂线是圆的切线;④过直径端点的垂线是圆的切线
A.1个 B.2个 C.3个 D.4个
8.如图,AB为⊙O的直径,OC为半径,切线CP与AB的延长线交于点P,PD平分∠CPA交AC于点D,则∠ADP的度数等于 .
9.如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD的值为 .
10.如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,且AB=AC,若CD=2,则OE的长为 .
11.如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 度.
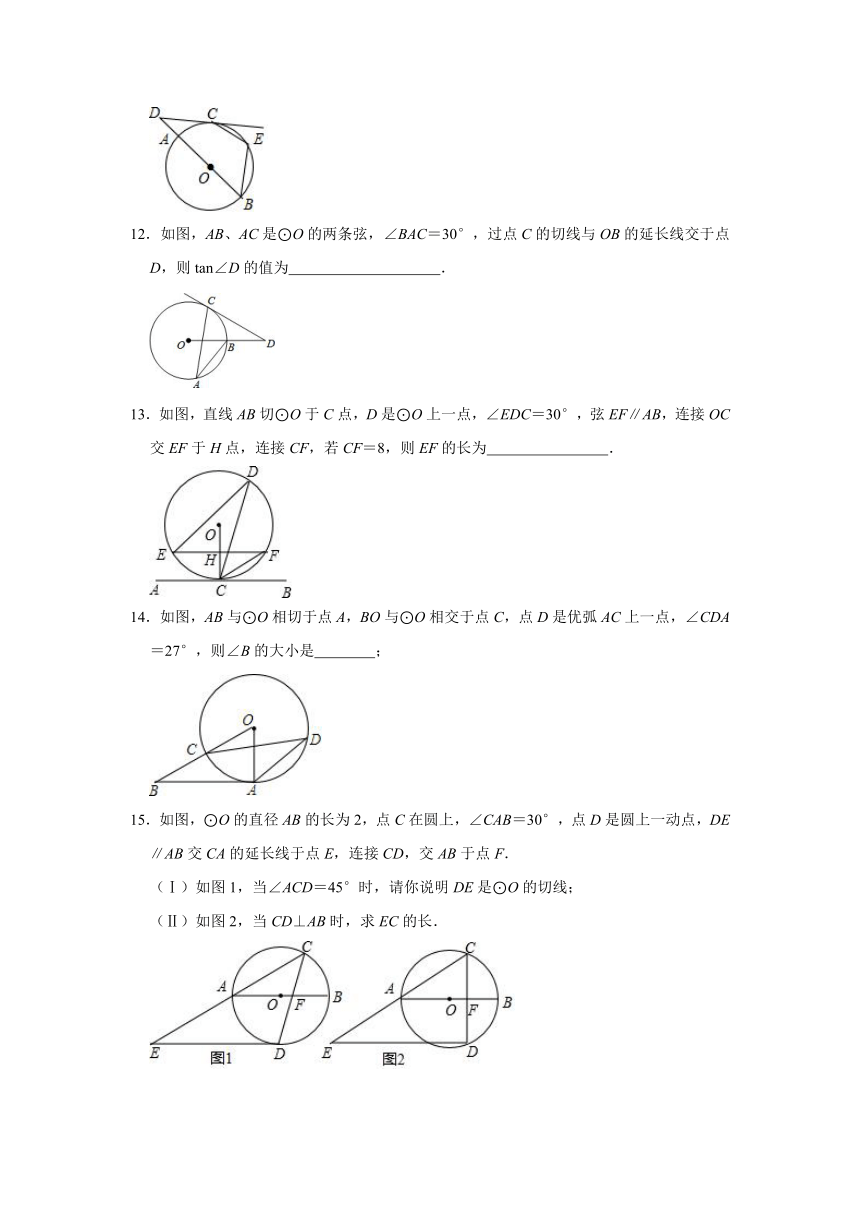
12.如图,AB、AC是⊙O的两条弦,∠BAC=30°,过点C的切线与OB的延长线交于点D,则tan∠D的值为 .
13.如图,直线AB切⊙O于C点,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于H点,连接CF,若CF=8,则EF的长为 .
14.如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是 ;
15.如图,⊙O的直径AB的长为2,点C在圆上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(Ⅰ)如图1,当∠ACD=45°时,请你说明DE是⊙O的切线;
(Ⅱ)如图2,当CD⊥AB时,求EC的长.
16.如图,以等腰△ABC的腰AB为⊙O的直径交底边BC于D,DE⊥AC于E.
求证:(1)DB=DC;
(2)DE为⊙O的切线
17.如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
18.如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
19.已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
20.如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,过A作AD⊥CD,D为垂足.
(1)求证:∠DAC=∠BAC;
(2)若AC=6,cos∠BAC=,求⊙O的直径.
21.如图,PA为⊙O的切线,A为切点,⊙O的割线PBC过点O与⊙O分别交于B、C,PA=8cm,PB=4cm,求⊙O的半径.
22.如图,PA切⊙O于点A,割线PBC交⊙O于点B、C.
(1)求证:PA2=PB PC;
(2)割线PDE交⊙O于点D、E,且PB=BC=4,PE=6,求DE的长.
参考答案
1.解:∵AC=8cm,AB=10cm,
∴BC==6,
S△ABC=AC×BC=×6×8=24,
∴AB上的高为:24×2÷10=4.8,
即圆心到直线的距离是4.8,
∵r=4.5,
∴4.8>4.5
∴⊙C与直线AB相离,
故选:B.
2.解:设圆的半径为r,点O到直线l的距离为d,
∵d=6,r=5,
∴d>r,
∴直线l与圆相离.
故选:C.
3.解:连接OB,
∵BC与⊙O相切于点B,
∴OB⊥BC,
设⊙O的半径为r,
在Rt△OBC中,OB2+BC2=OC2,
即,
解得:r=2,
故选:B.
4.解:∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵∠C=36°,
∴∠AOC=54°,
∵OB=OD,
∴∠B=∠ODB,
∵∠AOC=∠B+∠ODB,
∴∠B=×54°=27°,
故选:A.
5.解:当AB=AC时,如图:连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∴CD=BD,
∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线.
所以B正确.
当CD=BD时,AO=BO,∴OD是△ABC的中位线,
∴OD∥AC
∵DE⊥AC
∴DE⊥OD
∴DE是⊙O的切线.
所以C正确.
当AC∥OD时,∵DE⊥AC,∴DE⊥OD.
∴DE是⊙O的切线.
所以D正确.
故选:A.
6.解:A、经过半径的外端点且垂直于这条半径的直线是圆的切线;可能经过圆心,故本选项错误;
B、圆的切线的判定定理:经过直径的端点且垂直于这条直径的直线是圆的切线;故本选项正确,故不符合题意;
C、圆的切线垂直于经过切点的半径;故本选项正确,故不符合题意;
D、经过切点且垂直于切线的直线为圆的直径,所以它经过圆心;故本选项正确,故不符合题意;
故选:A.
7.解:①圆的切线垂直于半径;错误,应该是圆的切线垂直于过切点的半径;
②圆的切线垂直于过切点的半径;正确;
③过半径端点的垂线是圆的切线;错误;应该是过半径的外端的垂线是圆的切线;
④过直径端点的垂线是圆的切线,正确;
故选:B.
8.解:∵OA=OC,
∴∠A=∠OCA,又∠COP为△AOC的外角,
∴∠COP=∠A+∠OCA=2∠A,
∵PD为∠CPA的平分线,
∴∠CPD=∠APD=∠CPO,即∠CPO=2∠APD,
由PC切⊙O于点C,得到OC⊥PC,即∠OCP=90°,
∴∠COP+∠CPO=90°,
∴2∠A+2∠APD=2(∠A+∠APD)=90°,
∴∠A+∠APD=45°,
∴∠ADP=180°﹣45°=135°.
故答案为:135°.
9.解:∵∠C=90°,BC=3,AC=4
∴AB=5
∵⊙O是内切圆
∴由切线长定理设BF=BD=x,AF=AE=y,CE=CD=z
∴△ABC周长可以表示为3+4+5=2x+2y+2z
∴x+y+z=6
∴BD=6﹣(y+z)=6﹣(AE+EC)=2
DC=6﹣(AF+FB)=6﹣5=1
∵CA、CB与⊙O相切
∴∠ODC=∠OEC=90°
∵∠C=90°
∴四边形OECD为矩形
∵CD=DE
∴四边形OECD为正方形
∴OD=DC=1
Rt△BOD中
tan∠OBD=
故答案为:
10.解:连接OA、AD,如右图所示,
∵BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,
∴∠DAB=90°,∠OAC=90°,
∵AB=AC,
∴∠B=∠C,
在△ACO和△BAD中,
,
∴△ACO≌△BAD(ASA),
∴AO=AD,
∵AO=OD,
∴AO=OD=AD,
∴△AOD是等边三角形,
∴∠ADO=∠DAO=60°,
∴∠B=∠C=30°,∠OAE=30°,∠DAC=30°,
∴AD=DC,
∵CD=2,
∴AD=2,
∴点O为BD的中点,OE∥AD,OE⊥AB,
∴OE=,
故答案为:.
11.解:连接OC,
∵DC切⊙O于C,
∴∠DCO=90°,
∵∠D=40°,
∴∠COB=∠D+∠DCO=130°,
∴的度数是130°,
∴的度数是360°﹣130°=230°,
∴∠BEC==115°,
故答案为:115.
12.解:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∵∠BAC=30°,
∴∠BOC=60°,
∴∠D=30°,
∴tan∠D=,
故答案为:.
13.解:∵直线AB切⊙O于C点,
∴OC⊥AB,
∵EF∥AB,
∴OH⊥EF,
∴EH=HF,
由圆周角定理得,∠F=∠EDC=30°,
∴HC=CF=4,
∴HF==4,
∴EF=2HF=8,
故答案为:8.
14.解:∵AB与⊙O相切于点A,
∴OA⊥BA.
∴∠OAB=90°.
∵∠CDA=27°,
∴∠BOA=54°.
∴∠B=90°﹣54°=36°.
故答案为:36°
15.(1)证明:如图1中,连接OD.
∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是⊙O切线.
(2)如图2中,连接BC,
∵CD⊥AB,AB是直径,
∴CF=DF,∠ACB=90°,
在RT△ACB中,∠CAB=30°,AB=2,
∴AC=,
∵AB∥ED,CF=DF,
∴AE=AC=EC,
∴EC=2AC=2.
16.证明:(1)连AD,
∵AB是直径,
∴∠ADB=90°,AD⊥BC,
又AB=AC,
∴D为BC中点,
即DB=DC;
(2)连OD,
∵D为BC中点,OA=OB,
∴OD为△ABC中位线,
∴OD∥AC
又∵DE⊥AC于E,
∴∠ODE=∠DEC=90°,
∴DE为圆的切线.
17.(1)解:连接OB,
∵弦AB⊥OC,劣弧AB的度数为120°,
∴弧BC与弧AC的度数为:60°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OC=2;
(2)∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.
18.(1)证明:连接OB.
∵OA=OB,∴∠A=∠OBA,
又∵BC=PC,
∴∠P=∠CBP,
∵OP⊥AD,
∴∠A+∠P=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=180°﹣(∠OBA+∠CBP)=90°,
∵点B在⊙O上,
∴直线BC是⊙O的切线,
(2)解:如图,连接DB.
∵AD是⊙O的直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△AOP,
∴=,即 =,AP=9,
∴BP=AP﹣BA=9﹣2=7.
19.(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵∠P=35°,
∴∠AB=90°﹣35°=55°.
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
20.证明:(1)连接BC,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠BAC=90°,
∵直线CD与⊙O相切于点C,
∴∠ACD=∠B,∠OCD=90°,
∵AD⊥CD,
∴∠CAD+∠ACD=90°,
∴∠DAC=∠BAC;
(2)∵cos∠BAC=,
∴=,
∵AC=6,
∴AB=10,
故⊙O的直径为10.
21.解:连接OA,
设⊙O的半径为rcm,
则r2+82=(r+4)2,
解得r=6,
∴⊙O的半径为6cm.
22.解:(1)连接AB、AC、BO、AO,
∵PA切⊙O于点A,
∴PA⊥AO,即∠PAB+∠BAO=90°,
又∵2∠BAO+∠O=180°,
∴∠PAB=∠O,
∵∠C=∠O,
∴∠PAB=∠C,
∴△PAB∽△PCA,
∴,
即PA2=PB PC.
(2)∵PA2=PB PC,
同理,PA2=PD PE,
∴PD PE=PB PC,
且PB=BC=4,PE=6,
∴,
即DE=PE﹣PD=6﹣=.
1.在Rt△ABC中,∠C=90°,AC=8cm,AB=10cm,以C为圆心,以9cm长为直径的⊙C与直线AB的位置关系为( )
A.相交 B.相离 C.相切 D.相离或相交
2.已知⊙O的半径为5cm,点O到同一平面内直线l的距离为6cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.如图,已知BC与⊙O相切于点B,CO的延长线交⊙O于点A,连接AB,若BC=2,AC=6,则⊙O的半径为( )
A.1.5 B.2 C.2.5 D.3
4.如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D.连接BD,∠C=36°,则∠B的度数是( )
A.27° B.30° C.36° D.54°
5.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC C.CD=DB D.AC∥OD
6.下列命题中,假命题是( )
A.经过半径的端点且垂直于这条半径的直线是圆的切线
B.经过直径的端点且垂直于这条直径的直线是圆的切线
C.经过圆心且垂直于切线的直线必经过切点
D.经过切点且垂直于切线的直线必经过圆心
7.下列说法中错误的有( )
①圆的切线垂直于半径;②圆的切线垂直于过切点的半径;③过半径端点的垂线是圆的切线;④过直径端点的垂线是圆的切线
A.1个 B.2个 C.3个 D.4个
8.如图,AB为⊙O的直径,OC为半径,切线CP与AB的延长线交于点P,PD平分∠CPA交AC于点D,则∠ADP的度数等于 .
9.如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD的值为 .
10.如图,BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,且AB=AC,若CD=2,则OE的长为 .
11.如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC= 度.
12.如图,AB、AC是⊙O的两条弦,∠BAC=30°,过点C的切线与OB的延长线交于点D,则tan∠D的值为 .
13.如图,直线AB切⊙O于C点,D是⊙O上一点,∠EDC=30°,弦EF∥AB,连接OC交EF于H点,连接CF,若CF=8,则EF的长为 .
14.如图,AB与⊙O相切于点A,BO与⊙O相交于点C,点D是优弧AC上一点,∠CDA=27°,则∠B的大小是 ;
15.如图,⊙O的直径AB的长为2,点C在圆上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(Ⅰ)如图1,当∠ACD=45°时,请你说明DE是⊙O的切线;
(Ⅱ)如图2,当CD⊥AB时,求EC的长.
16.如图,以等腰△ABC的腰AB为⊙O的直径交底边BC于D,DE⊥AC于E.
求证:(1)DB=DC;
(2)DE为⊙O的切线
17.如图,已知P是⊙O外一点,PO交圆O于点C,OC=CP=2,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
18.如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P.点C在OP上,且BC=PC.
(1)求证:直线BC是⊙O的切线;
(2)若OA=3,AB=2,求BP的长.
19.已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
20.如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,过A作AD⊥CD,D为垂足.
(1)求证:∠DAC=∠BAC;
(2)若AC=6,cos∠BAC=,求⊙O的直径.
21.如图,PA为⊙O的切线,A为切点,⊙O的割线PBC过点O与⊙O分别交于B、C,PA=8cm,PB=4cm,求⊙O的半径.
22.如图,PA切⊙O于点A,割线PBC交⊙O于点B、C.
(1)求证:PA2=PB PC;
(2)割线PDE交⊙O于点D、E,且PB=BC=4,PE=6,求DE的长.
参考答案
1.解:∵AC=8cm,AB=10cm,
∴BC==6,
S△ABC=AC×BC=×6×8=24,
∴AB上的高为:24×2÷10=4.8,
即圆心到直线的距离是4.8,
∵r=4.5,
∴4.8>4.5
∴⊙C与直线AB相离,
故选:B.
2.解:设圆的半径为r,点O到直线l的距离为d,
∵d=6,r=5,
∴d>r,
∴直线l与圆相离.
故选:C.
3.解:连接OB,
∵BC与⊙O相切于点B,
∴OB⊥BC,
设⊙O的半径为r,
在Rt△OBC中,OB2+BC2=OC2,
即,
解得:r=2,
故选:B.
4.解:∵AC是⊙O的切线,
∴AB⊥AC,
∴∠OAC=90°,
∵∠C=36°,
∴∠AOC=54°,
∵OB=OD,
∴∠B=∠ODB,
∵∠AOC=∠B+∠ODB,
∴∠B=×54°=27°,
故选:A.
5.解:当AB=AC时,如图:连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,
∴CD=BD,
∵AO=BO,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线.
所以B正确.
当CD=BD时,AO=BO,∴OD是△ABC的中位线,
∴OD∥AC
∵DE⊥AC
∴DE⊥OD
∴DE是⊙O的切线.
所以C正确.
当AC∥OD时,∵DE⊥AC,∴DE⊥OD.
∴DE是⊙O的切线.
所以D正确.
故选:A.
6.解:A、经过半径的外端点且垂直于这条半径的直线是圆的切线;可能经过圆心,故本选项错误;
B、圆的切线的判定定理:经过直径的端点且垂直于这条直径的直线是圆的切线;故本选项正确,故不符合题意;
C、圆的切线垂直于经过切点的半径;故本选项正确,故不符合题意;
D、经过切点且垂直于切线的直线为圆的直径,所以它经过圆心;故本选项正确,故不符合题意;
故选:A.
7.解:①圆的切线垂直于半径;错误,应该是圆的切线垂直于过切点的半径;
②圆的切线垂直于过切点的半径;正确;
③过半径端点的垂线是圆的切线;错误;应该是过半径的外端的垂线是圆的切线;
④过直径端点的垂线是圆的切线,正确;
故选:B.
8.解:∵OA=OC,
∴∠A=∠OCA,又∠COP为△AOC的外角,
∴∠COP=∠A+∠OCA=2∠A,
∵PD为∠CPA的平分线,
∴∠CPD=∠APD=∠CPO,即∠CPO=2∠APD,
由PC切⊙O于点C,得到OC⊥PC,即∠OCP=90°,
∴∠COP+∠CPO=90°,
∴2∠A+2∠APD=2(∠A+∠APD)=90°,
∴∠A+∠APD=45°,
∴∠ADP=180°﹣45°=135°.
故答案为:135°.
9.解:∵∠C=90°,BC=3,AC=4
∴AB=5
∵⊙O是内切圆
∴由切线长定理设BF=BD=x,AF=AE=y,CE=CD=z
∴△ABC周长可以表示为3+4+5=2x+2y+2z
∴x+y+z=6
∴BD=6﹣(y+z)=6﹣(AE+EC)=2
DC=6﹣(AF+FB)=6﹣5=1
∵CA、CB与⊙O相切
∴∠ODC=∠OEC=90°
∵∠C=90°
∴四边形OECD为矩形
∵CD=DE
∴四边形OECD为正方形
∴OD=DC=1
Rt△BOD中
tan∠OBD=
故答案为:
10.解:连接OA、AD,如右图所示,
∵BD是⊙O的直径,BA是⊙O的弦,过点A的切线交BD延长线于点C,OE⊥AB于E,
∴∠DAB=90°,∠OAC=90°,
∵AB=AC,
∴∠B=∠C,
在△ACO和△BAD中,
,
∴△ACO≌△BAD(ASA),
∴AO=AD,
∵AO=OD,
∴AO=OD=AD,
∴△AOD是等边三角形,
∴∠ADO=∠DAO=60°,
∴∠B=∠C=30°,∠OAE=30°,∠DAC=30°,
∴AD=DC,
∵CD=2,
∴AD=2,
∴点O为BD的中点,OE∥AD,OE⊥AB,
∴OE=,
故答案为:.
11.解:连接OC,
∵DC切⊙O于C,
∴∠DCO=90°,
∵∠D=40°,
∴∠COB=∠D+∠DCO=130°,
∴的度数是130°,
∴的度数是360°﹣130°=230°,
∴∠BEC==115°,
故答案为:115.
12.解:连接OC,
∵CD是⊙O的切线,
∴∠OCD=90°,
∵∠BAC=30°,
∴∠BOC=60°,
∴∠D=30°,
∴tan∠D=,
故答案为:.
13.解:∵直线AB切⊙O于C点,
∴OC⊥AB,
∵EF∥AB,
∴OH⊥EF,
∴EH=HF,
由圆周角定理得,∠F=∠EDC=30°,
∴HC=CF=4,
∴HF==4,
∴EF=2HF=8,
故答案为:8.
14.解:∵AB与⊙O相切于点A,
∴OA⊥BA.
∴∠OAB=90°.
∵∠CDA=27°,
∴∠BOA=54°.
∴∠B=90°﹣54°=36°.
故答案为:36°
15.(1)证明:如图1中,连接OD.
∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是⊙O切线.
(2)如图2中,连接BC,
∵CD⊥AB,AB是直径,
∴CF=DF,∠ACB=90°,
在RT△ACB中,∠CAB=30°,AB=2,
∴AC=,
∵AB∥ED,CF=DF,
∴AE=AC=EC,
∴EC=2AC=2.
16.证明:(1)连AD,
∵AB是直径,
∴∠ADB=90°,AD⊥BC,
又AB=AC,
∴D为BC中点,
即DB=DC;
(2)连OD,
∵D为BC中点,OA=OB,
∴OD为△ABC中位线,
∴OD∥AC
又∵DE⊥AC于E,
∴∠ODE=∠DEC=90°,
∴DE为圆的切线.
17.(1)解:连接OB,
∵弦AB⊥OC,劣弧AB的度数为120°,
∴弧BC与弧AC的度数为:60°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OC=2;
(2)∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.
18.(1)证明:连接OB.
∵OA=OB,∴∠A=∠OBA,
又∵BC=PC,
∴∠P=∠CBP,
∵OP⊥AD,
∴∠A+∠P=90°,
∴∠OBA+∠CBP=90°,
∴∠OBC=180°﹣(∠OBA+∠CBP)=90°,
∵点B在⊙O上,
∴直线BC是⊙O的切线,
(2)解:如图,连接DB.
∵AD是⊙O的直径,
∴∠ABD=90°,
∴Rt△ABD∽Rt△AOP,
∴=,即 =,AP=9,
∴BP=AP﹣BA=9﹣2=7.
19.(1)解:∵AB是⊙O的直径,AP是⊙O的切线,
∴AB⊥AP,
∴∠BAP=90°;
又∵∠P=35°,
∴∠AB=90°﹣35°=55°.
(2)证明:如图,连接OC,OD、AC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角),
∴∠ACP=90°;
又∵D为AP的中点,
∴AD=CD(直角三角形斜边上的中线等于斜边的一半);
在△OAD和△OCD中,
,
∴△OAD≌△OCD(SSS),
∴∠OAD=∠OCD(全等三角形的对应角相等);
又∵AP是⊙O的切线,A是切点,
∴AB⊥AP,
∴∠OAD=90°,
∴∠OCD=90°,即直线CD是⊙O的切线.
20.证明:(1)连接BC,OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠BAC=90°,
∵直线CD与⊙O相切于点C,
∴∠ACD=∠B,∠OCD=90°,
∵AD⊥CD,
∴∠CAD+∠ACD=90°,
∴∠DAC=∠BAC;
(2)∵cos∠BAC=,
∴=,
∵AC=6,
∴AB=10,
故⊙O的直径为10.
21.解:连接OA,
设⊙O的半径为rcm,
则r2+82=(r+4)2,
解得r=6,
∴⊙O的半径为6cm.
22.解:(1)连接AB、AC、BO、AO,
∵PA切⊙O于点A,
∴PA⊥AO,即∠PAB+∠BAO=90°,
又∵2∠BAO+∠O=180°,
∴∠PAB=∠O,
∵∠C=∠O,
∴∠PAB=∠C,
∴△PAB∽△PCA,
∴,
即PA2=PB PC.
(2)∵PA2=PB PC,
同理,PA2=PD PE,
∴PD PE=PB PC,
且PB=BC=4,PE=6,
∴,
即DE=PE﹣PD=6﹣=.
