五四制鲁教版数学七年级上册期末测试题(一)(含答案)
文档属性
| 名称 | 五四制鲁教版数学七年级上册期末测试题(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-20 10:23:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
五四制鲁教版数学七年级上册期末测试题(一)
时间:100分钟 满分:100分
一、选择题(每小题3分,共36分)
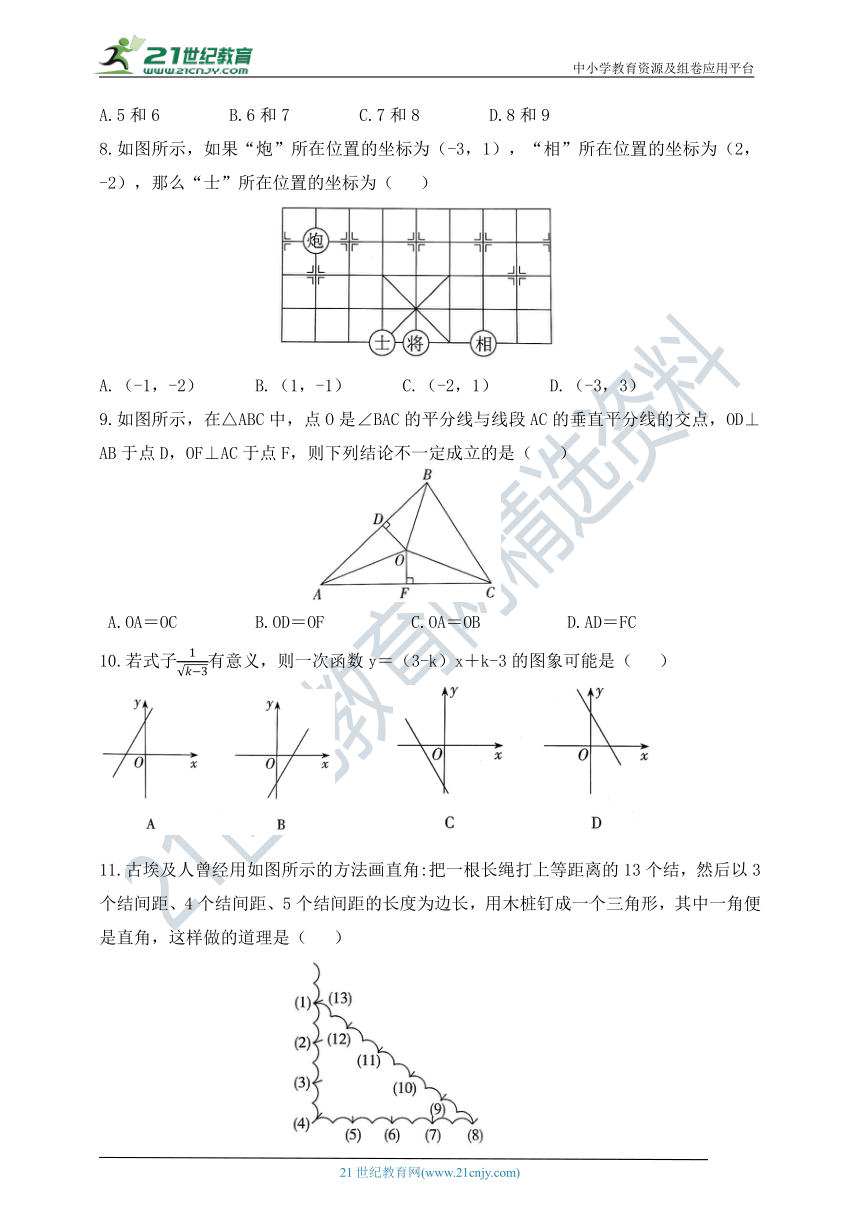
1.下列四个标志中,是轴对称图形的是( )
2.以下列长度的各组线段为边,能组成三角形的是( )
A.2cm,3cm,6cm B.3cm,4cm,8cm C.5cm,6cm,10cm D.5cm,6cm,11cm
3.在实数,,,0.0,π,,0.301300130001…(3与1之间依次增加一个0)中,无理数的个数为( )
A.3 B.4 C.5 D.2
4.如图所示,在网格图中选择一个格子涂上阴影,使得整个图形是以虚线所在直线为对称轴的轴对称图形,则应把阴影涂在图中标有数字_________的格子内.( )
A.1 B.2 C.3 D.4
5.用直尺和圆规作一个角等于已知角,如图所示,能得出∠A′O′B′=∠AOB的依据是( )
A.SAS B.SSS C.ASA D.AAS
6.下列叙述正确的是( )
A.0.4的平方根是±0.2 B.-(-2)3的立方根不存在
C.±6是36的算术平方根 D.-27的立方根是-3
7.在下面哪两个整数之间( )
A.5和6 B.6和7 C.7和8 D.8和9
8.如图所示,如果“炮”所在位置的坐标为(-3,1),“相”所在位置的坐标为(2,-2),那么“士”所在位置的坐标为( )
A.(-1,-2) B.(1,-1) C.(-2,1) D.(-3,3)
9.如图所示,在△ABC中,点O是∠BAC的平分线与线段AC的垂直平分线的交点,OD⊥AB于点D,OF⊥AC于点F,则下列结论不一定成立的是( )
A.OA=OC B.OD=OF C.OA=OB D.AD=FC
10.若式子有意义,则一次函数y=(3-k)x+k-3的图象可能是( )
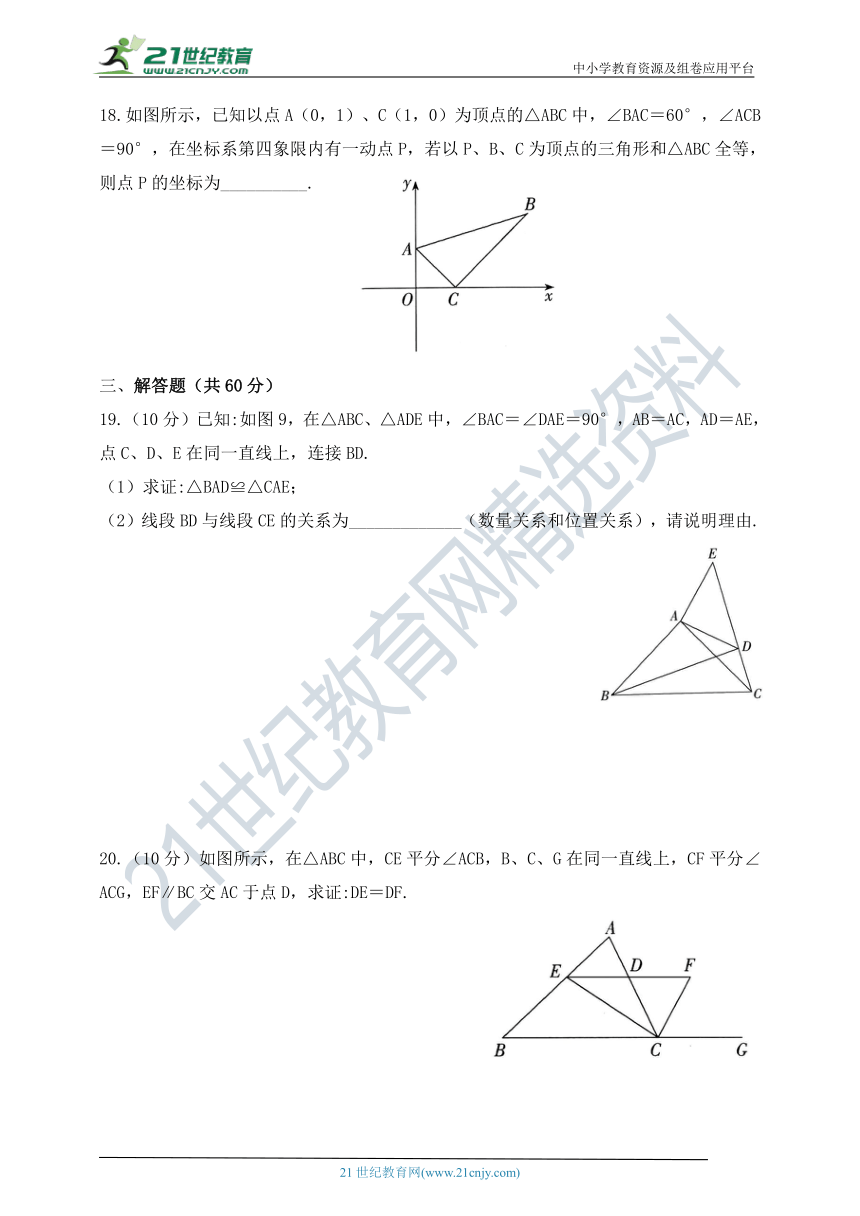
11.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形任意两边之和大于第三边,任意两边之差小于第三边
D.如果三角形两边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
12.全民健身的今天,散步是大众喜欢的运动甲、乙两人在绿道上同时从同一起点以各自
的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行甲、乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( )
A.60米/分,40米/分 B.80米/分,60米/分
C.80米/分,40米/分 D.120米/分,80米/分
二、填空题(每小题4分,共24分)
13.用计算器计算:(结果精确到0.01)
14.已知点A(a+2,5)与点B(5,b)关于x轴对称,则a-b=___________.
15.__________.
16.已知金属棒的长度l(cm)是温度t(℃)的一次函数现有一根金属棒,在0℃时的长度是200cm,温度每升高1℃,它就伸长0.002cm,则这根金属棒的长度(cm)与温度t(℃)的函数关系式为______________.
17.如图所示,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是________ cm.
18.如图所示,已知以点A(0,1)、C(1,0)为顶点的△ABC中,∠BAC=60°,∠ACB=90°,在坐标系第四象限内有一动点P,若以P、B、C为顶点的三角形和△ABC全等,则点P的坐标为__________.
解答题(共60分)
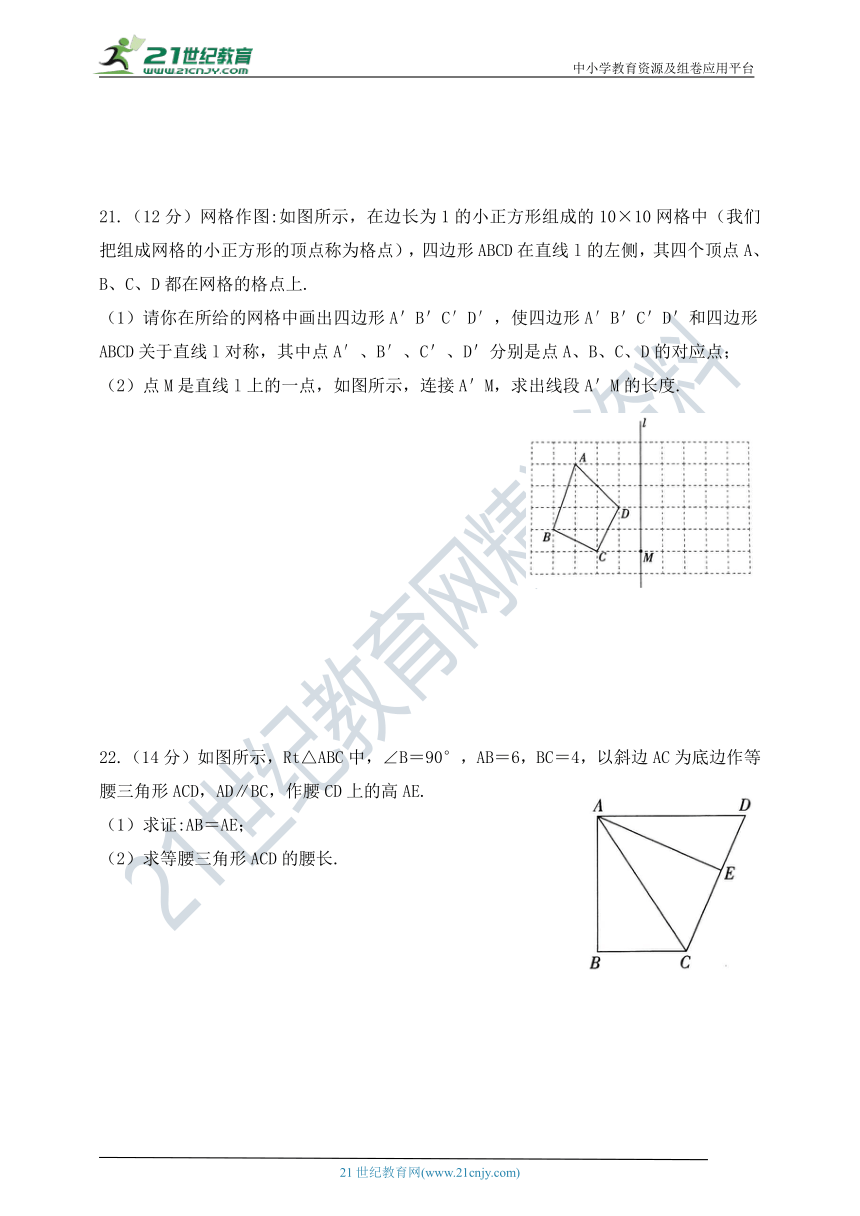
19.(10分)已知:如图9,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)线段BD与线段CE的关系为_____________(数量关系和位置关系),请说明理由.
20.(10分)如图所示,在△ABC中,CE平分∠ACB,B、C、G在同一直线上,CF平分∠ACG,EF∥BC交AC于点D,求证:DE=DF.
21.(12分)网格作图:如图所示,在边长为1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A、B、C、D都在网格的格点上.
(1)请你在所给的网格中画出四边形A'B'C′D′,使四边形A′B'C'D'和四边形ABCD关于直线l对称,其中点A′、B′、C'、D'分别是点A、B、C、D的对应点;
(2)点M是直线l上的一点,如图所示,连接A'M,求出线段A'M的长度.
22.(14分)如图所示,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,AD∥BC,作腰CD上的高AE.
(1)求证:AB=AE;
(2)求等腰三角形ACD的腰长.
23.(14分)甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
(1)直接写出甲组加工零件的数量y与时间x之间的函数关系式:_________________;
(2)求a的值;
(3)甲、乙两组加工出的零件合在一起装箱,每满300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱.
参考答案
一、选择题
1.D 2.C 3.A 4.C 5.B 6.D 7.B 8.A 9.C 10.D
11.D 12.A
二、填空题
13. 1.57 14. 8 15. 16. 17. 80 18.(2,-1)
三、解答题
19.解析 (1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,∴∠BAD=∠CAE,
在△BAD和△CAE中,∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,∴BD=CE,∠BDA=∠E,
∵∠E+∠ADE=90°,∴∠BDA+∠ADE=∠BDE=90°,即BD⊥CE.
20.证明 ∵CE平分∠ACB,∴∠ACE=∠BCE.
∵CF平分∠ACG,∴∠ACF=∠GCF.
∵EF∥BC,∴∠GCF=∠F,∠BCE=∠CEF.
∴∠DCE=∠CED,∠F=∠DCF.
∴CD=ED,CD=DF.∴DE=DF.
21.解析 (1)如图,四边形A'B'C'D′即为所求.
(2)如图,A'M==5.
22.解析 (1)证明:由题意知DA=DC,∴∠DAC=∠DCA,
∵AD∥BC,∴∠DAC=∠BCA,∴∠ACB=∠DCA,
∵AE⊥CD,∴∠AEC=90°,∴∠B=∠AEC,
在△ABC和△AEC中,∴△ABC≌△AEC(AAS),∴AB=AE.
(2)∵△ABC≌△AEC,∴AE=AB=6,CE=CB=4,
设DC=x,则DA=x,DE=x-4,由勾股定理,得DE2+AE2=DA2,
即(x-4)2+62=x2,解得x=,
即等腰三角形ACD的腰长为 .
23.解析 (1)y=60x(0≤x≤6)
(2)由题图知,当0≤x≤2时,乙组的加工速度是每小时加工50件,
∵乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍,
∴更换设备后,乙组的加工速度是每小时加工100件,
∴a=100+100×(4.8-2.8)=300.
(3)乙组加工零件的数量y与时间x的函数关系式为
y=
当0≤x≤2时,60x+50x=300,解得x=(不合题意,舍去);
当2<x≤28时,100+60x=300,解得x=(不合题意,舍去);
当2.8<x≤4.8时,60x+100x-180=300,解得x=3,
∴经过3小时恰好装满第1箱.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
五四制鲁教版数学七年级上册期末测试题(一)
时间:100分钟 满分:100分
一、选择题(每小题3分,共36分)
1.下列四个标志中,是轴对称图形的是( )
2.以下列长度的各组线段为边,能组成三角形的是( )
A.2cm,3cm,6cm B.3cm,4cm,8cm C.5cm,6cm,10cm D.5cm,6cm,11cm
3.在实数,,,0.0,π,,0.301300130001…(3与1之间依次增加一个0)中,无理数的个数为( )
A.3 B.4 C.5 D.2
4.如图所示,在网格图中选择一个格子涂上阴影,使得整个图形是以虚线所在直线为对称轴的轴对称图形,则应把阴影涂在图中标有数字_________的格子内.( )
A.1 B.2 C.3 D.4
5.用直尺和圆规作一个角等于已知角,如图所示,能得出∠A′O′B′=∠AOB的依据是( )
A.SAS B.SSS C.ASA D.AAS
6.下列叙述正确的是( )
A.0.4的平方根是±0.2 B.-(-2)3的立方根不存在
C.±6是36的算术平方根 D.-27的立方根是-3
7.在下面哪两个整数之间( )
A.5和6 B.6和7 C.7和8 D.8和9
8.如图所示,如果“炮”所在位置的坐标为(-3,1),“相”所在位置的坐标为(2,-2),那么“士”所在位置的坐标为( )
A.(-1,-2) B.(1,-1) C.(-2,1) D.(-3,3)
9.如图所示,在△ABC中,点O是∠BAC的平分线与线段AC的垂直平分线的交点,OD⊥AB于点D,OF⊥AC于点F,则下列结论不一定成立的是( )
A.OA=OC B.OD=OF C.OA=OB D.AD=FC
10.若式子有意义,则一次函数y=(3-k)x+k-3的图象可能是( )
11.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互余
B.三角形内角和等于180°
C.三角形任意两边之和大于第三边,任意两边之差小于第三边
D.如果三角形两边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
12.全民健身的今天,散步是大众喜欢的运动甲、乙两人在绿道上同时从同一起点以各自
的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行甲、乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是( )
A.60米/分,40米/分 B.80米/分,60米/分
C.80米/分,40米/分 D.120米/分,80米/分
二、填空题(每小题4分,共24分)
13.用计算器计算:(结果精确到0.01)
14.已知点A(a+2,5)与点B(5,b)关于x轴对称,则a-b=___________.
15.__________.
16.已知金属棒的长度l(cm)是温度t(℃)的一次函数现有一根金属棒,在0℃时的长度是200cm,温度每升高1℃,它就伸长0.002cm,则这根金属棒的长度(cm)与温度t(℃)的函数关系式为______________.
17.如图所示,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是________ cm.
18.如图所示,已知以点A(0,1)、C(1,0)为顶点的△ABC中,∠BAC=60°,∠ACB=90°,在坐标系第四象限内有一动点P,若以P、B、C为顶点的三角形和△ABC全等,则点P的坐标为__________.
解答题(共60分)
19.(10分)已知:如图9,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)线段BD与线段CE的关系为_____________(数量关系和位置关系),请说明理由.
20.(10分)如图所示,在△ABC中,CE平分∠ACB,B、C、G在同一直线上,CF平分∠ACG,EF∥BC交AC于点D,求证:DE=DF.
21.(12分)网格作图:如图所示,在边长为1的小正方形组成的10×10网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A、B、C、D都在网格的格点上.
(1)请你在所给的网格中画出四边形A'B'C′D′,使四边形A′B'C'D'和四边形ABCD关于直线l对称,其中点A′、B′、C'、D'分别是点A、B、C、D的对应点;
(2)点M是直线l上的一点,如图所示,连接A'M,求出线段A'M的长度.
22.(14分)如图所示,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,AD∥BC,作腰CD上的高AE.
(1)求证:AB=AE;
(2)求等腰三角形ACD的腰长.
23.(14分)甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
(1)直接写出甲组加工零件的数量y与时间x之间的函数关系式:_________________;
(2)求a的值;
(3)甲、乙两组加工出的零件合在一起装箱,每满300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱.
参考答案
一、选择题
1.D 2.C 3.A 4.C 5.B 6.D 7.B 8.A 9.C 10.D
11.D 12.A
二、填空题
13. 1.57 14. 8 15. 16. 17. 80 18.(2,-1)
三、解答题
19.解析 (1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,∴∠BAD=∠CAE,
在△BAD和△CAE中,∴△BAD≌△CAE(SAS).
(2)BD=CE,BD⊥CE,理由如下:
由(1)知,△BAD≌△CAE,∴BD=CE,∠BDA=∠E,
∵∠E+∠ADE=90°,∴∠BDA+∠ADE=∠BDE=90°,即BD⊥CE.
20.证明 ∵CE平分∠ACB,∴∠ACE=∠BCE.
∵CF平分∠ACG,∴∠ACF=∠GCF.
∵EF∥BC,∴∠GCF=∠F,∠BCE=∠CEF.
∴∠DCE=∠CED,∠F=∠DCF.
∴CD=ED,CD=DF.∴DE=DF.
21.解析 (1)如图,四边形A'B'C'D′即为所求.
(2)如图,A'M==5.
22.解析 (1)证明:由题意知DA=DC,∴∠DAC=∠DCA,
∵AD∥BC,∴∠DAC=∠BCA,∴∠ACB=∠DCA,
∵AE⊥CD,∴∠AEC=90°,∴∠B=∠AEC,
在△ABC和△AEC中,∴△ABC≌△AEC(AAS),∴AB=AE.
(2)∵△ABC≌△AEC,∴AE=AB=6,CE=CB=4,
设DC=x,则DA=x,DE=x-4,由勾股定理,得DE2+AE2=DA2,
即(x-4)2+62=x2,解得x=,
即等腰三角形ACD的腰长为 .
23.解析 (1)y=60x(0≤x≤6)
(2)由题图知,当0≤x≤2时,乙组的加工速度是每小时加工50件,
∵乙组在工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍,
∴更换设备后,乙组的加工速度是每小时加工100件,
∴a=100+100×(4.8-2.8)=300.
(3)乙组加工零件的数量y与时间x的函数关系式为
y=
当0≤x≤2时,60x+50x=300,解得x=(不合题意,舍去);
当2<x≤28时,100+60x=300,解得x=(不合题意,舍去);
当2.8<x≤4.8时,60x+100x-180=300,解得x=3,
∴经过3小时恰好装满第1箱.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
